基于惯量辨识PI自整定永磁伺服电机控制

马立新, 范洪成, 徐镇乾，黄阳龙，周尚珺玺

(上海理工大学 光电信息与计算机工程学院，上海200093)

基于惯量辨识PI自整定永磁伺服电机控制

马立新, 范洪成, 徐镇乾，黄阳龙，周尚珺玺

(上海理工大学 光电信息与计算机工程学院，上海200093)

针对传统PID控制存在的缺陷以及永磁同步电机运行中惯量变化问题，提出了永磁伺服电机惯量辨识PI自整定控制方法。测定电机在匀加速过程中不同时刻转速值，通过转动惯量辨识算法得出转动惯量大小，分析转动惯量与速度环中的参数关系来自动整定控制参数。利用MATLAB工具建立系统仿真模型，并与传统PID控制进行了对比，结果表明：惯量辨识PI自整定控制方法实现了启动高速化、无超调及强抗干扰能力，具有很好的动静态性能，能广泛应用在高精度控制系统中，对解决惯量易变系统提供了一种控制依据。

永磁同步电机；惯量辨识；PI自整定

0 引言

目前，随着稀土永磁材料的诞生，永磁同步电机(PMSM)[1]在伺服系统的应用越来越广泛，大量的工业生产都以PMSM作为驱动电机，如高性能机器人、数控机床、矿山机械等[2]。PMSM经过长时间运行以及干扰噪声等因素的影响，导致电机参数发生变化，控制效果达不到工业标准。其中参数发生变化的一个主要原因是电机转动惯量的变化[3]。转动惯量过大会导致电机运行不稳定，响应速度慢。转动惯量过小，虽然系统响应速度加快，但同时会导致超调量变大，产生震荡。

传统的PMSM控制策略采用的是PID控制，其中PID控制中比例、积分、微分三个参数值与电机自身的参数关联紧密，而电机运行中参数是时变的，所以参数辨识对电机的控制十分关键。

采用惯量辨识PI自整定永磁伺服电机控制策略，即测定电机在匀加速时4个不同时刻转速值，通过电机在d、q坐标系下的电磁转矩和机械方程得出转动惯量大小，根据转动惯量的大小对速度环进行自动整定[4]。与传统PID控制进行对比，仿真结果表明该方法使系统具有更好的动静态性能。

1 永磁同步电机坐标变换及其数学模型

1.1 永磁同步电机坐标变换

永磁同步电机原始模型复杂，通过坐标变换，简化电机矢量结构。坐标变换公式如下：

三相-两相变换：即三相绕组A、B、C和两相绕组α、β之间的变换，简称3/2变换。

(1)

静止两相-旋转正交变换：即从静止两相正交坐标系α、β到旋转正交坐标系d、q的变换，简称2s/2r变换。

(2)

式中：θ表示d轴与A轴之间的夹角。

1.2 永磁同步电机数学模型

图1为两级贴面式永磁同步电机空间矢量图，其基本方程如下：

图1 永磁同步电机电压空间矢量图

电压方程为：

(3)

磁链方程为：

(4)

转矩方程为：

Te=3p(ψfiq+(Ld-Lq)id)/2

(5)

式中：D=d/dt为微分算子；rs为定子电阻；Ld、Lq分别为d轴和q轴电感；Ud、Uq分别为d轴和q轴电压；ω为转子角速度；id、iq分别为d轴和q轴电流；Ψm、Ψd、Ψq、Ψf分别为永磁体、d轴、q轴、转子磁通。

2 惯量辨识PI自整定原理

2.1 转动惯量辨识PI自整定控制方法

传统PI控制其控制参数是根据具体的数学模型而确立的，不能跟随系统参数的变化自动整定，无法满足工业的控制要求。而采用惯量辨识PI自整定控制方法，在电机匀加速过程中，通过分析计算其转动惯量的大小对PI控制器中的控制参数进行整定，可以达到实时控制[5～7]。结构如图2所示。

图2 转动惯量辨识PI自整定控制原理图

2.2 转动惯量辨识算法

在d、q坐标系下电磁转矩Te与交轴电流iq成正比，其电磁转矩方程为：

Te=Npψfiq

(6)

当不计摩擦时，其机械方程为：

(7)

式中：TL为负载转矩，J为转动惯量。

为保证电机正常运行，必须限制其最大电流，当采取id=0控制方式时，只需控制iq即可，取iq(max)=2in。当电机以最大电流稳定运行时，即Te=2Tn时，由式(7)得电机加速度为：

(8)

测定电机匀加速过程中t1、t2时刻转子速度ω1、ω2，则有：

(9)

取iq(max)=in。当电机以最大电流稳定运行时，即Te=Tn时。测定电机匀加速过程中t3、t4时刻转子速度ω3、ω4，且t4-t3=t2-t1，则有：

(10)

根据式(9)、(10)得出电机转动惯量方程为：

(11)

根据转动惯量辨识算法可知：电机必须处于匀加速过程才能测量转动惯量的大小，但电机实际运行过程中不可能以匀加速运行，因此为实现惯量辨识算法，本文在电机启动过程中取10个主采样点，每个采样点又分4个副采样点，其中4个副采样点时间要求间隔短，这样在很短的时间间隔内近似认为电机处于匀加速运行状态，从而通过式(11)即可得出惯量J的大小。

2.3 转动惯量整定PI

永磁同步电机一般情况下均选取双闭环控制方式。当电流环采用I型系统设计时，闭环传递函数为：

(12)

式中：T∑i=Toi+Ts：其中Toi是电流滤波时间常数，Ts为整流装置滞后时间常数，KI为电流环开环增益，KI=1/2T∑i。

对于高阶系统，一般都要进行降阶处理，即忽略传递函数中的高次项，则闭环传递函数Wcli(s)变为：

(13)

对于转速环，在转速调节器(ASR)中应设有积分环节，以达到转速无静差；但是，电机运行过程中可能会受到各种各样的干扰，因此，在干扰发生后应再设定一个积分环节，以保证其抗干扰效果好；所以转速环应设计成II型系统，ASR应采用PI调节器，其传递函数为：

(14)

式中：Kn为转速调节器比例系数；τn为转速调节器时间常数。

图3 转速环结构图

这样，调速系统的开环传递函数为：

(15)

由于转速调节器是按照II型系统设计的，其中参数Kn和τn满足下式关系：

τn=2T∑ih

(16)

(17)

式中：h为中频带宽，h的大小与系统动态性能有关，h越小，则系统抗扰性越好；当h<5时会使系统震荡次数增加；因此，选取h=5最好。则PI中的控制参数为：

(18)

(19)

式中：h、Kτ、T∑i均为常数。由式(18)、(19)可以得出，转动惯量J对PI中的控制参数有重要的作用，因此可以通过转动惯量J来整定PI参数。

3 仿真结果

3.1 电机参数

分别对传统PID控制和惯量辨识PI自整定控制策略进行仿真，启动阶段，给定负载转矩为1 N·m；在0.5 s时,负载转矩变为 4 N·m。选取电机参数如表1所示。

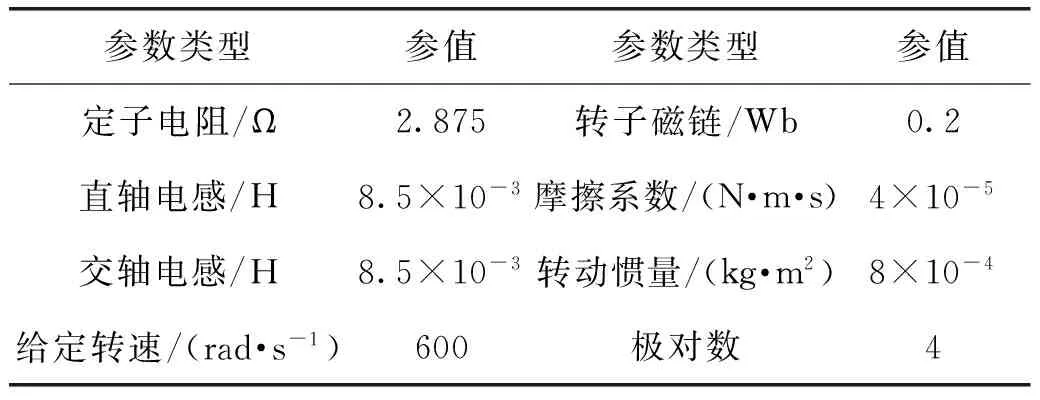
表1 电机参数

3.2 系统运行过程

仿真中控制方式为：Id=0控制，转速设定为600 rad/s，通过测定电机匀加速过程中4个不同时刻转速值，将转速值送入到转动惯量辨识模块中，来控制转速环中PI控制参数，根据电压空间矢量脉宽调制原理[8～11]，逆变出三相电流来驱动电机。结构如图4所示。

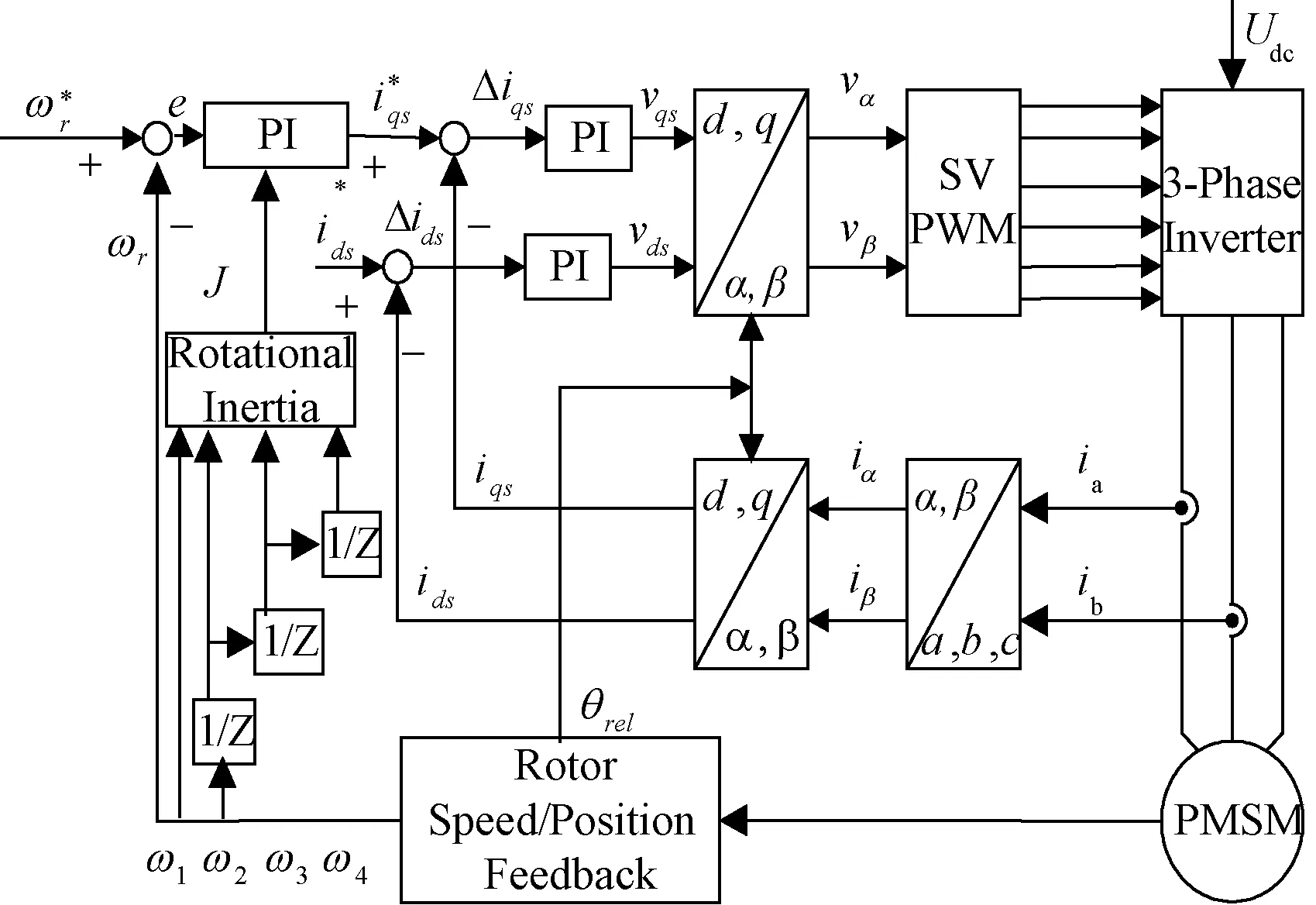
图4 惯量辨识PI自整定结构图

3.3 仿真曲线分析

从仿真曲线可以看出，传统PI控制下转速超调量大，因超调量大，电机容易发生抖动，转子会撞击电机外壳，易毁坏电机；而在惯量辨识PI自整定控制方式下，转速响应快、无超调，实现了电机启动高速化，如图5所示。

图5 两种控制模式下转速仿真曲线

在扰动发生时，传统PID控制下转矩脉动很大，会产生很大的冲击电流，容易对电机造成损害，甚至烧毁电机。而惯量辨识PI自整定控制，转矩波形变化平缓，实现了系统快速稳定性，如图6所示。

图6 两种控制模式下转矩波形曲线

两种控制模式下，其仿真结果对比如表2所示。

本文选取10个主采样点，启动开始时转动惯量突然变化很大，然后迅速减小，最后逐渐上升到稳定值，其惯量辨识结果如表3所示。

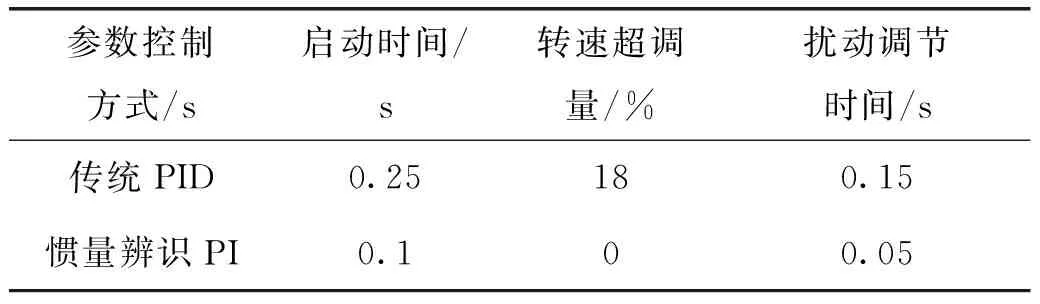
表2 仿真结果对比

表3 惯量辨识结果

4 结论

永磁同步电机惯量辨识PI自整定控制方法对系统实时控制，实现了启动高速化、无超调及强抗干扰能力，克服了传统PID控制的缺陷。有利于提高数控机床以及高精密系统的效率和控制精度，改善了惯量易变系统的性能，在工程中具有良好的应用前景。

[1]陈伯时.电力拖动自动控制系统[M]. 北京：机械工业出版社, 2010.

[2]李烨.永磁同步电动机伺服系统研究现状及应用前景[J].微电机,2001,34(4):30-33.

[3]刘旭，阮毅，张朝艺.一种异步电机转动惯量辨识方法[J].电机与控制应用,2009,36(9)：1-3.

[4]赵希梅，郭庆鼎. PMSM伺服系统的转动惯量辨识和控制器参数优化[J].组合机应与自动化加工技术，2009，(7)：75-77.

[5]Wu Y, Fangy Y, Liu L, et al. Global dynamic sliding mode control of PMSM speed servo systems base on extended state observer[C]. Control Conference (CCC),2013, 32nd Chinese IEEE,2013:4432-4437.

[6]蒋学程，彭侠夫.小转动惯量永磁同步电机电流环内模控制[J].控制工程，2011，18(3):331-334.

[7]刘竹.带PI参数自整定的永磁同步电机伺服系统的设计与实现[D].长沙:湖南大学,2013:24-36.

[8]王宝忠，王维，王波. 基于模糊自整定PI的PMSM伺服系统的仿真研究[J]. 电力科学与工程,2013,29(7):18-22.

[9]彭咏龙，黄潇潇，李亚斌.基于SVPWM的高功率因数三相混合开关型整流电路研究[J].电力科学与工程，2013，29(6):23-29.

[10]陈玲，纪萍，朱虹. 基于脉冲阻塞原理的多功能交交变频系统的PWM研究[J].华北电力大学学报(自然科学版)，2014，41(6):39-45.

[11]王春民,嵇艳鞠,栾卉，等. MATLAB/SIMULINK永磁同步电机矢量控制系统仿真[J]. 吉林大学学报(信息科学版),2009,27(1):17-22.

Research on Inertia Identification of PI Auto-tuning PMSM Servo System

Ma Lixin, Fan Hongcheng, Xu Zhenqian, Huang Yanglong, Zhou Shangjunxi

(School of Optical-Electrical and Computer Engineering, University of Shanghai for Science and Technology,Shanghai 200093, China)

Aiming at the drawbacks of the traditional PID control and the problems of the changes of moment of inertia of PMSM servo system, a new method of moment of inertia identification of PI auto-tuning PMSM servo system is proposed. After the motor speed under the uniform acceleration motion having been measured, this method was employed to calculate the moment of inertia by using optimization. Then the control parameters can be auto-tuned by analysing the parameters' relationship between moment of inertia and speed loop. Data collected from MATLAB simulation model were compared with those acquired from traditional PID control. It leads to the conclusion that the new method can acquire high-speed starting, no overshoot and strong anti-interference abilities and perform better in both dynamic and static states. Accordingly, it can be widely applied in high precision control system and regarded as a theoretical foundation for solving the problem of variability of inertia.

permanent magnet synchronous motor; inertia identification; PI auto-tuning

2015-05-08。

上海张江国家自主创新重点项目(201310-PI-B2-008)；沪江基金(C14002)。

马立新(1960-)，男，教授，主要从事电力系统稳定性、配电网规划与优化配置、电力负荷需求分析与预测方法、调速系统智能控制等方面的教学与科研工作，E-mali：malx_aii@sina.com。

TM351

A

10.3969/j.issn.1672-0792.2015.09.006