Hochschild Cohomology Rings of Temperley-Lieb Algebras∗

Huanhuan LI Yunge XU Yuan CHEN

1 Introduction

The Temperley-Lieb algebras were first introduced in 1971 in[24]to study the single bond transfer matrices for the ice model and the Potts model.Later they were independently found by Jones when he characterized the algebras arising from the tower construction of semisimple algebras in the study of subfactors(see[18]).These algebras have played a central role in the discovery by Jones of his new polynomial invariant of knots and links(see[19]),and in the subsequent developments over the past four decades relating to knot theory,topological quantum field theory,and statistical physics(see[20]).Their relationship with knot theory comes from their role in the Definition of the Jones polynomial.The theory of quantum invariants of links nowadays involves many research fields.Thus,many important kinds of algebras related to the invariants of braids or links,such as Birman Wenzl algebras(see[5]),Hecke algebras and Brauer algebras,have been of great interest in mathematics and physics.They are all deformations of certain group algebras or other well-known algebras.

Let K be a field and m a positive integer.Recall that the Temperley-Lieb algebra Am(δ)for δ∈ K is defined to be a K-algebra with identity generated by t1,t2,···,tm−1subject tothe relations:

It was shown in[25]that a block of a non-semisimple Temperley-Lieb algebra is Morita equivalent to the quotient algebra A=Am=KQ/I given by the quiver

and the relations I=〈αi+1αi,βiβi+1,βi+1αi+1−αiβi,αm−1βm−1|i=1,2,···,m−2〉.As was shown in[26],the non-trivial block of the representation- finite q-Schur algebras Sq(n,r)with n≥r is also Morita equivalent to an algebra of the form Am.

Hochschild cohomology HH∗(A,M)of A with coefficients in M was introduced in[16]in order to classify,up to equivalence,all extensions of A with Kernel M,which is one-to-one correspondence with HH2(A,M).Many other applications of this cohomology have been discovered since then(see[15]).For example,separable algebras are characterized by the fact that their Hochschild(cohomology)dimension is zero,that is,HH1(A,M)=0 for every bimodule M(see[16]);the deformation theory of an algebra is controlled by its Hochschild cohomology as a graded Lie algebra under the Gerstenhaber bracket(see[11]);Hochschild cohomology is also closely related to simple connectedness,formal smoothness(or quasi-freeness in literature)(see[1,22])and so on.It is well known that HH∗(A)is endowed with the so-called Gerstenhaber algebra structure under the cup product

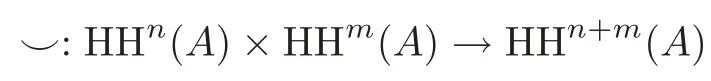
and the Gerstenhaber Lie bracket

However,for most finite dimensional algebras,little is known about the Hochschild cohomology groups and even less about the Hochschild cohomology rings(see[2,4,7–10,13,27]).

Since Hochschild cohomology is invariant under Morita equivalence(see[15]),to describe the Hochschild cohomology rings of both the Temperley-Lieb algebras and the representation- finite q-Schur algebras Sq(n,r)for n≥r,it is sufficient to deal with the basic algebra A defined as above.The K-dimensions of Hochschild cohomology groups of A were obtained in[17]by a long exact sequence of cohomology groups relating to a homological epimorphism of K-algebras,but there K-bases were not given.We begin the paper by giving a minimal projective resolution of A as an Ae-module,and then apply it to obtain K-bases of the cohomology groups in terms of parallel paths.In Section 4 we give an explicit description of the “comultiplicative” map Δ:P→P⊗AP to determine the cup product of HH∗(A)using the composition

P→P⊗AP→A⊗AA→A.

As a consequence,we will give an explicit presentation of the multiplicative structure of HH∗(A)under the cup product by generators and relations.

2 The Minimal Projective Bimodule Resolution

Throughout the paper we always assume that A is the algebra defined as in the introduction.We denote by eithe trivial path at the vertex i.Given a path p in Q,we denote by o(p)and t(p)the origin and the terminus of p respectively.

We will employ the strategy due to Green et al in[12,14]to construct a minimal projective Ae-module resolution of A.Seti=1,2,···,m.For 1≤n≤2m−2,one defines the following elements recursively:

Noticing that gl.dimA=2m−2,one takesif n>2m−2.Note thatis just an algebraic sum of paths of length n with the original i and containing exactly r arrows of type α.Denote by gnthe set of elements of the formThen,

For 3≤n≤2m−2,when n=2k,

when n=2k+1,

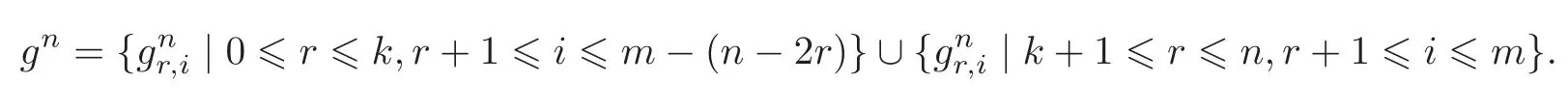
In particular,we have

In order to define the differential δ,we need the following lemma so that we have two di ff erent ways of expressing the elements of the set gnin terms of the elements of the set gn−1.The proof of Lemma 2.1 is straightforward and therefore omitted.

Lemma 2.1For n≤1,we have

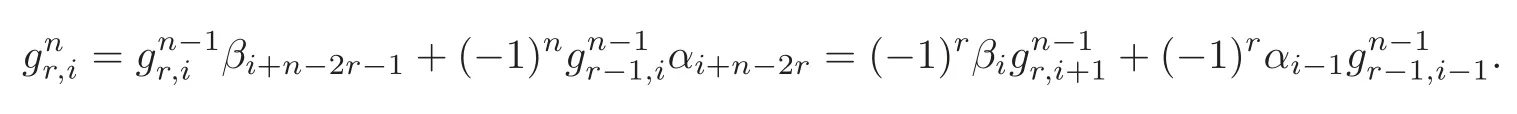
Denote⊗:=⊗K.define

and for 1≤n≤2m−2,δn:Pn→ Pn−1is given by

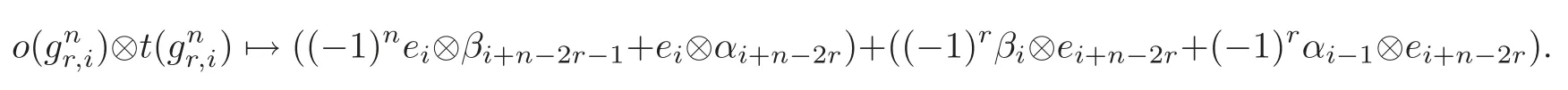
The following theorem follows immediately from Lemma 2.1 and[12,Theorem 2.1].

Theorem 2.1With the above notation,the complex

is a minimal projective Ae-resolution of A,where δ0:P0→ A is the multiplication map.

ProofLet X=g1and R=g2be the set of generators of I as above.Since A is a Koszul alg?ebra,by[3,Sect.9],it suffices to show that gnis a K-basis of the K-vector space

We f i rst show that all thebelong to Kninductively.It is trivial for n=2.Assume that the assertion holds for n−1 and we prove it for n.By the induction hypothesis and the formula(2.1),The induction hypothesis and Lemma 2.1 show thatThe assertion follows from the fact that Kn=RXn−2∩ Xn−2R ∩XKn−1∩ Kn−1X.

Next,gnis K-linearly independent since they have distinct supports.Also,the quadratic duality A!=kQ/I⊥of A is isomorphic to the Yoneda algebra E(A)of A,where I⊥is the ideal of KQ generated by R⊥={β1α1,βi+1αi+1+ αiβi|i=1,2,···,m − 2}.So the Betti number of the minimal projective resolution of A over Aeis

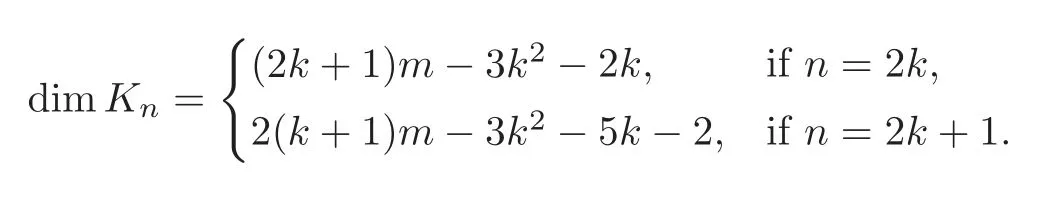
Hence gnis a K-basis of Kn.Then the result follows.

3 Hochschild Cohomology Groups

This section is devoted to finding K-bases of the Hochschild cohomology groups of A based on the minimal projective Ae-resolution constructed in the previous section.

Applying HomAe(−,A)to the minimal resolution(P,δ),we have the complex

Let B={e1,e2,···,em,β1,β2,···,βm−1,α1,α2,···,αm−1,β1α1,β2α2,···,βm−1αm−1}be a K-basis of algebra A,and K(B//gn)denote the vector space with a K-basis B//gn={(b,gnr,i)|We say that two paths α and β are parallel if o(α)=o(β)and t(α)=t(β).

The following lemma is immediate,see[6,21]for details.

Lemma 3.1HomAe(Pn,A)∼=K(B//gn)as vector spaces.

ProofIt is easy to see that

as vector spaces.

We fix an isomorphism φ :K(B//gn) → HomAe(Pn,A)sending(b,γ) ∈ (B//gn)to the Ae-homomorphism f(b,γ)∈ HomAe(Pn,A),which assigns o(γ)⊗ t(γ)to b,and zero otherwise.The cochain complex above changes into

where we still denote bythe induced linear maps.

Lemma 3.2Kerhas a K-basisand dimKIm=m−1.

ProofUnder the K-bases,

B//g0={(e1,e1),(e2,e2),···,(em,em),(β1α1,e1),(β2α2,e2),···,(βm−1αm−1,em−1)}and

B//g1={(β1,β1),(β2,β2),···,(βm−1,βm−1)(α1,−α1),(α2,−α2),···,(αm−1,−αm−1}.It is not difficult to calculate the matrix of the linear map δ∗1which is

with the right m−1 columns zero.It is clear that rankA1=m−1,and hence dimKIm=rankA1=m−1,and dimKKer=|B//g0|−rankA1=(m+m−1)−(m−1)=m.One can easily check that

Noticing that HHn(A)=Kerwe next find out a K-basis of the kernel space Kerand the image space Imfor n>0,respectively.They will be discussed in four cases.

Case I:n=4t,t≠0.Set

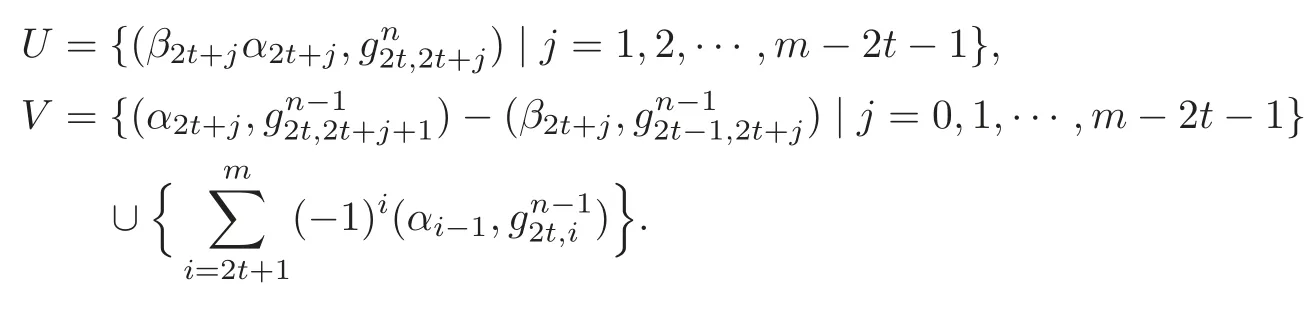
Case II:n=4t+1,t≠0.Set

Case III:n=4t+2.Set

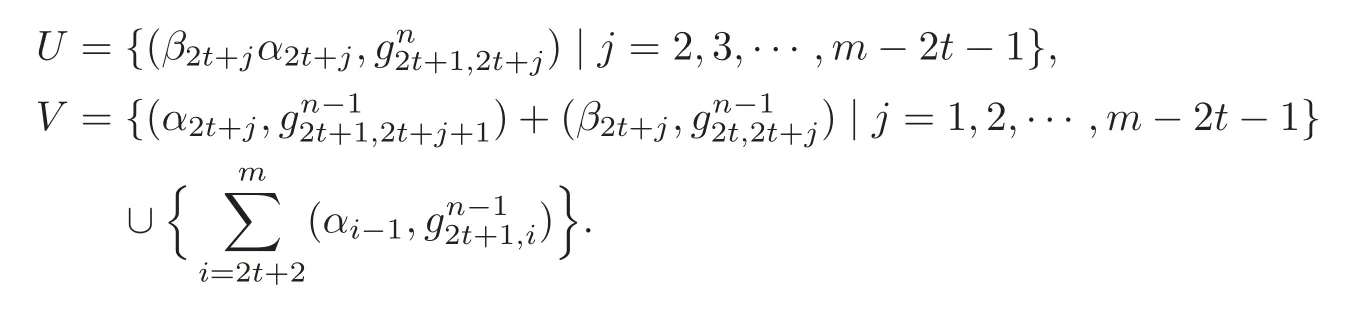
Case IV:n=4t+3.Set

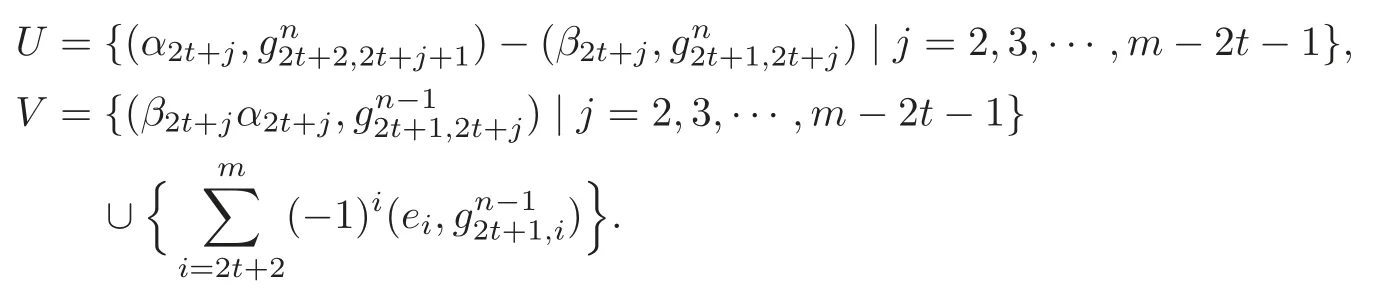
Lemma 3.3U forms a K-basis of Imand V forms a K-basis of Ker.

ProofWe only prove the case I,and the other cases are similar and their proofs are omitted here.It is not difficult to calculate the matrix of the linear mapunder the K-bases B//gn−1=The matrix Anis

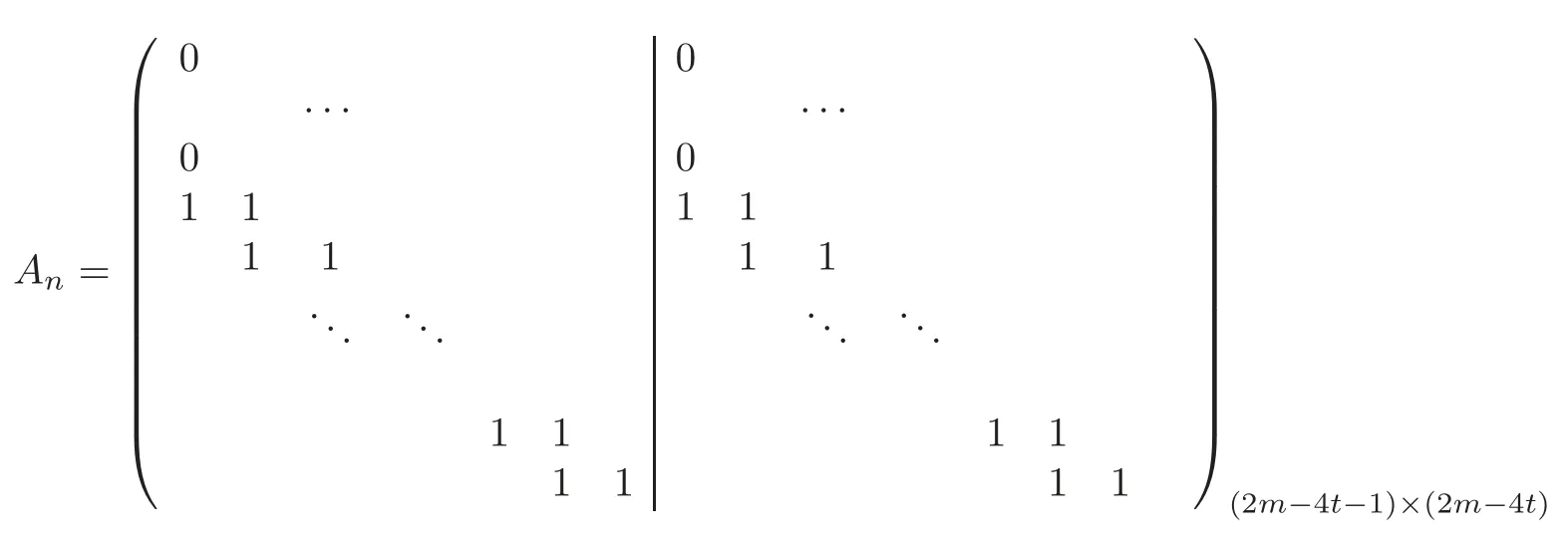
whose first m−2t rows are zero.The rank of Anis m−2t−1 and hence dimKIm=rankAn=m−2t−1 and dimKKer=|B//gn−1|−dimKIm=2(m−2t)−(m−2t−1)=m−2t+1.

It is easy to see that

可靠性监控(图2)主要用于监控汽车使用和维修过程的可靠性，同时也监控系统功能，例如结构改变原始记录、维修记录、故障库、限值数据、排除故障数据、质量数据、费用数据、零部件和用于管理维修过程的其他各种程序等。

Since the setis K-linear independent and has m−2t−1 elements,it is a K-basis of Im.

Clearly,

It follows that

which is obviously K-linear independent and has m−2t+1 elements,so it is a K-basis of Ker.The proof is finished.

Now it is a position to give a K-basis of the Hochschild cohomological space HHn(A).

Theorem 3.1Let A=KQ/I be the K-algebra defined as in the introduction.Then we have

(1)dimKHHi(A)=

(2)HH0(A)has a basis

HH4t(A)has a basis

HH4t+1(A)has a basis

HH4t+2(A)has a basis

HH4t+3(A)has a basis

Here these basis elements represent the representatives of the corresponding elements in HHn(A).

ProofIt follows from Lemmas 3.2–3.3 and the fact that HHi(A)=Kerdirectly.

Remark 3.1The dimension of the Hochschild cohomological space HHn(A) was obtained by de la Pea and Xi in[17]in a different way.

4 The Cup Product

In this section we will describe the multiplicative structure of the Hochschild cohomology ring of A in terms of parallel paths.In[23]it was shown that for any projective Ae-resolution P of a f i nite dimensional algebra A,there exists a unique(up to homotopy)chain map Δ :P → P⊗AP lifting the identity.P gives rise to a “cup product” of two elements η in HHm(A)and θ in HHn(A)by using the composition

coinciding with the ordinary cup product and being independent of the projective resolution P of A and the chain map Δ.

The following lemma provides an explicit description of the so-called“comultiplicative structure” of the generators of each Pnin(P,δ),which is key to def i ning a chain map Δ.

Lemma 4.1For any given p=0,1,···,n,we have

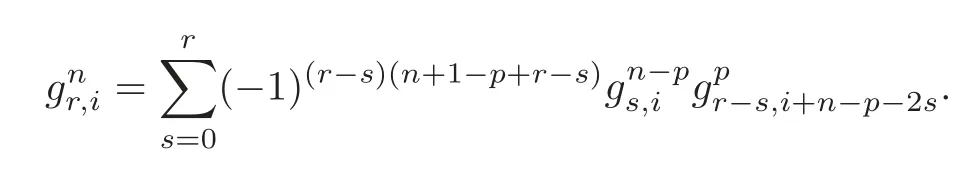
ProofWe use induction on p.There is nothing to prove provided that p=0.If p=1,thenwhich is just the de fining formula of

Suppose now that the formula holds true for p=k.We consider the case p=k+1.By the induction hypothesis and the formula(2.1),we have

The result follows.

The lemma allows us to give the Definition of the map Δ :P → P⊗AP.First we recall the tensor product chain complex(P⊗AP,D)of(P,δ).Its n-th object isand the differential Dn:(P⊗AP)n→(P⊗AP)n−1is given byBy abuse of notations,we denote by othe corresponding idempotent eo(gnr,i)(resp.),and bythe generator oof Pn.

Definition 4.1The A-A-bimodule map Δ =(Δn):P → P⊗AP is defined by

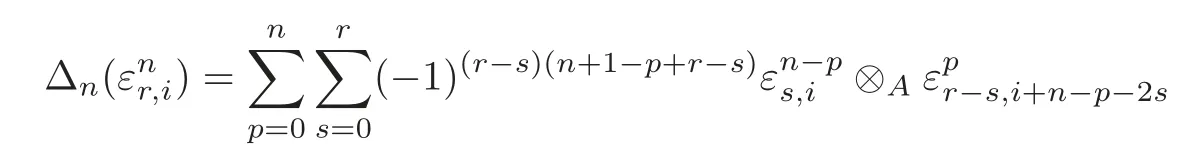
for 0≤n≤2m−2 and the other Δnare all zero.

Lemma 4.2The map Δ :(P,δ)→ (P⊗AP,D)defined as above is a chain map.

ProofTo prove the result,it suffices to show that the diagram

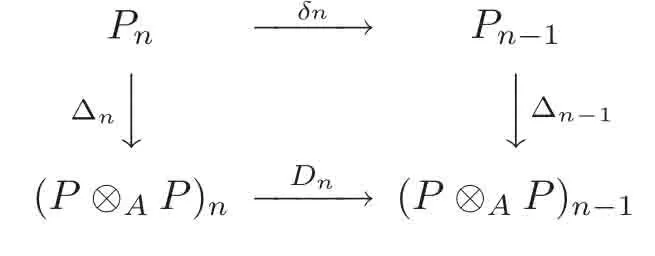
is commutative for n≥1.

Letdenote the element of Pt⊗APn−1−t.By the Definition of Δ and=(−1)nei⊗βi+n−2r−1+ei⊗αi+n−2r+(−1)rβi⊗ei+n−2r+(−1)rαi−1⊗ei+n−2r,we have

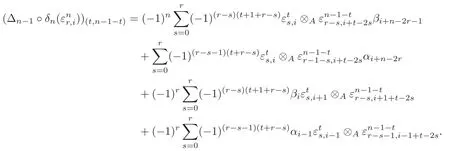
On the other hand,noting that

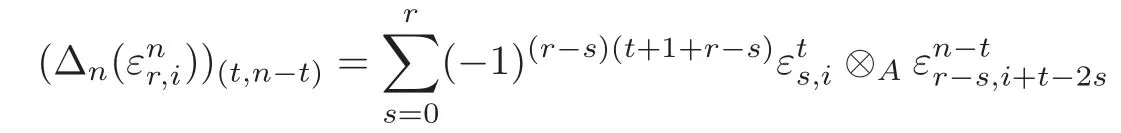
and

we can directly check that

and thus Δn−1δn=DnΔnas desired.The proof is finished.

In order to give an explicit description of the Hochschild cohomology ring of A,we first give the cup product on the level of cochains,which is essentially juxtaposition of parallel paths up to sign.

Lemma 4.3Let A=KQ/I be the K-algebra defined as in the introduction.Then

Hereis viewed as 0 whenever b1b2∈I.

ProofLet ηn1=and ηn2=Using the composition

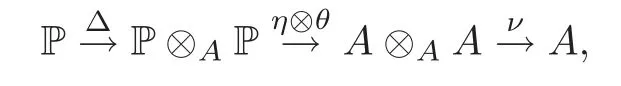
we have

When s≠r1or i≠k,we haveAnd when r−s≠r2or j≠k+n1−2s,we haveThus,only in the case of s=r1,i=k,r−s=r2and j=i+n1−2r1we haveBy the isomorphism of Lemma 3.1,it is easy to see that in the case of j=i+n1− 2r1,we haveand otherwise is zero.

Theorem 4.1Let A=KQ/I be the K-algebra defined as in the introduction.

(1)is the identity of HH∗(A),and for any ηj=(βjαj,ej)∈ HH0(A),ξ∈ HH∗(A),ξ/∈K,we have ηj︶ξ=ξ︶ηj=0.

(2)Let ηn1and ηn2be the unique basis elements of HHn1(A)and HHn2(A)with n1n2>0,respectively.We have

ProofIt follows from Lemma 4.3 directly.

Now we can give a description of the multiplication structure of the Hochschild cohomology ring of A by giving an explicit presentation by generators and relations.Let x1,x2,···,xm−1,y,z be the indeterminates of degree 0,0,···,0,1,2 respectively.Let Λ =K[x1,x2,···,xm−1,y,z]/J,where J is the two-sided ideal of the polynomial algebra K[x1,x2,···,xm−1,y,z]generated by

xixj=0, xiy=0, xiz=0, 1≤i,j≤m−1, y2=0, zm=0, yzm−1=0.

Theorem 4.2Let A=KQ/I be the K-algebra defined as in the introduction.Then HH∗(A) ∼= Λ.

ProofWe omit the symbol of the cup product ︶ of two elements of HH∗(A)for simplicity.Clearlyis the identity of HH∗(A).Denote

By Theorem 4.1,we have

Hence HH∗(A)can be generated by x1,x2,···,xm−1,y,z over K.Also,by Theorem 4.1,it is easy to find that any two elements in HH∗(A)are commutative and the following relations hold true:

xixj=0, xiy=0, xiz=0, 1≤i,j≤m−1, y2=0, zm=0, yzm−1=0.

Then we construct an epimorphic algebra homomorphism

ϕ :K[x1,x2,···,xm−1,y,z]→ HH∗(A)

sending x1,x2,···,xm−1,y,z to x1,x2,···,xm−1,y,z,respectively.Clearly,J ⊆ Kerϕ by the relations above.Noticing thatas a graded algebra satisfies that dimKΛ0=m and dimKΛj=1 for j≥ 1,we can immediately obtain that HH∗(A) ∼= Λ by comparing the dimensions of graded algebras HH∗(A)and Λ.

Remark 4.1Since the Hochschild cohomology of algebras is Morita-invariant,the above theorem describes the Hochschild cohomology rings of both the Temperley-Lieb algebras and the representation- finite q-Schur algebras Sq(n,r)for n≥r.

[1]Ardizzoni,A.,Menini,C.and Stefan,D.,Hochschild cohomology and smoothness in monoidal categories,J.Pure Appl.Algebra,208,2007,297–330.

[2]Buchweitz,R.O.,Green,E.L.,Snashall,N.and Solberg,Ø.,Multiplicative structures for Koszul algebras,Quart.J.Math.,59(4),2008,441–454.

[3]Bulter,M.C.R.and King,A.D.,Minimal resolution of algebras,J.Algebra,212,1999,323–362.

[4]Bustamante,J.C.,The cohomology structure of string algebras,J.Pure Appl.Algebra,204,2006,616–626.[5]Birman,J.and Wenzl,H.,Braids,link polynomials and a new algebra,Trans.Amer.Math.Soc.,313,1989,249–273.

[6]Cibils,C.,Rigidity of truncated quiver algebras,Adv.Math.,79,1990,18–42.

[7]Erdmann,K.and Holm,T.,Twisted bimodules and Hochschild cohomology for self-injective algebras of class An,Forum Math.,11,1999,177–201.

[8]Erdmann,K.and Schroll,S.,On the Hochschild cohomology of tame Hecke algebras,Arch.Math.,94,2010,117–127.

[9]Erdmann,K.and Snashall,N.,On Hochschild cohomology of preprojective algebras,II,J.Algebra,205,1998,413–434.

[10]Fan,J.M.and Xu,Y.G.,On Hochschild cohomology ring of Fibonacci algebras,Frontiers of Mathematics in China,1(4),2006,526–537.

[11]Gerstenhaber,M.,On the deformation of rings and algebras,Ann.Math.,79,1964,59–103.

[12]Green,E.L.,Hartman,G.,Marcos,E.N.and Solberg,Ø.,Resolutions over Koszul algebras,Arch.Math.,85,2005,118–127.

[13]Green,E.L.and Solberg,Ø.,Hochschild cohomology rings and triangular rings,Happel,D.and Zhang,Y.B.(eds.),Proceedings of the Ninth International Conference,Beijing Normal University Press,Beijing,2,2002,192–200.

[14]Green,E.L.,Solberg,Ø and Zacharia,D.,Minimal projective resolutions,Trans.Amer.Math.Soc.,353,2001,2915–2939.

[15]Happel,D.,Hochschild cohomology of finite-dimensional algebras,Lecture Notes in Mathematics,1404,Springer-Verlag,New York,1989,108–126.

[16]Hochschild,G.,On the cohomology groups of an associative algebra,Ann.Math.,46(1),1945,58–67.

[17]De la Pena,J.A.and Xi,C.C.,Hochschild cohomology of algebras with homological ideals,Tsukuba J.Math.,30(1),2006,61–80.

[18]Jones,V.F.R.,Index for subfactors,Invent.Math.,72,1983,1–25.

[19]Jones,V.F.R.,A polynomial invariant for links via von Neumann algebras,Bulletin of the Amer.Math.Soc.,129,1985,103–112.

[20]Kau ff man,L.H.,Knots in Physics,World Scientic Press,River Edge,NJ,1994.

[21]Strametz,C.,The Lie algebra structure on the first Hochschild cohomology group of a monomial algebra,Comptes Rendus Mathematique,334,2002,733–738.

[22]Skowro´nski,A.,Simply connected algebras and Hochschild cohomology,Can.Math.Soc.Proc.,14,1993,431–447.

[23]Siegel,S.F.and Witherspoon,S.J.,The Hochschild cohomology ring of a group algebra,Proc.London Math.Soc.,79(3),1999,131–157.

[24]Temperley,H.N.V.and Lieb,E.H.,Relations between percolation and colouring problems and other graph theoretical problems associated with regular planar lattices:Some exact results for the percolation problem,Proc.R.Soc.Lon.(Ser.A),322,1971,251–280.

[25]Westbury,B.W.,The representation theory of the Temperley-Lieb algebras,Math.Z.,219(4),1995,539–565.

[26]Xi,C.C.,On representation types of q-Schur algebras,J.Pure Appl.Algebra,84,1993,73–84.

[27]Xu,Y.G.and Xiang,H.L.,Hochschild cohomology rings of d-Koszul algebras,J.Pure Appl.Algebra,215,2011,1–12.