BSDEs with Jumps and Path-Dependent Parabolic Integro-Differential Equations∗
Falei WANG
1 Introduction
Linear backward stochastic differential equations(BSDEs for short)were introduced by Bismut[2]in 1973.Pardoux and Peng[16]established the existence and uniqueness theorem for nonlinear BSDEs under a standard Lipschitz condition in 1990.Then,Peng[18–19]and Pardoux and Peng[17]introduced the nonlinear Feynman-Kac formula,which provides a probabilistic representation for a wide class of semilinear partial differential equations(see also[13]).Since then,especially after the publication of the paper[11],in which the applications of BSDEs in finance were discussed,the theory of BSDE has received wide attention for both theoretical research and applications.
Recently,Dupire[7]introduced a new functional Itoˆ’s formula,which non-trivially generalized the classical one through a new notion-path derivative(see[4–6]for more general and systematic research).It extends the Itô stochastic calculus to functionals of a given process.It provides an excellent tool for the study of path-dependence.In fact,he showed that a smooth path functional solves a linear path-dependent PDE if its composition with a Brownian motion generates a martingale,which provided a functional extension of the classical Feynman-Kac formula.Moreover,by virtue of the BSDE approach,we obtained the existence and uniqueness of the smooth solution to the semilinear path-dependent PDE(see[21]).These methods are mainly based on stochastic calculus.
The aim of this paper is to generalize the above results to the case of BSDEs with both Brownian motion and a Poisson random measure.Consider the following BSDE with jumps:
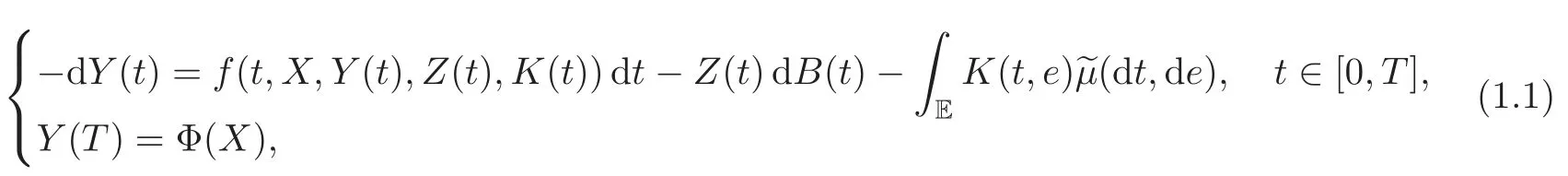
where X is a d-dimensional di ff usion satisfying the SDE
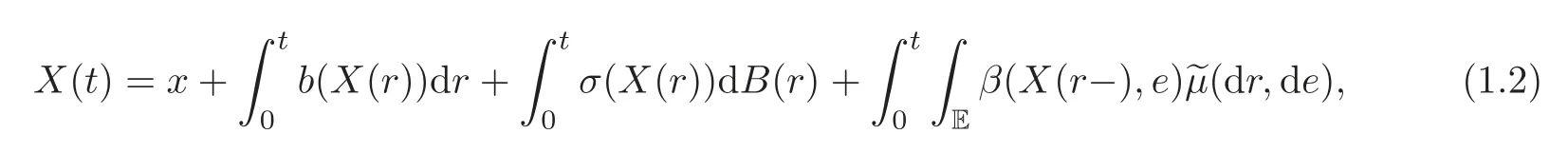
in which b:RdRd, σ :RdRd×d, β :Rd× ERdare some measurable functions,and f:Λ × Rn× Rn×d× L2(E,E,λ;Rn)Rnis a non-anticipative functional with respect to X.Note that(1.1)is“non-Markovian”.We will prove that under certain smooth assumptions(see Section 4)the solution(Y(t),Z(t),K(t))to(1.1)solves the following type of PDE,which is said to be path-dependent parabolic integro-differential equations(PIDEs for short).For each l∈ {1,···,n},
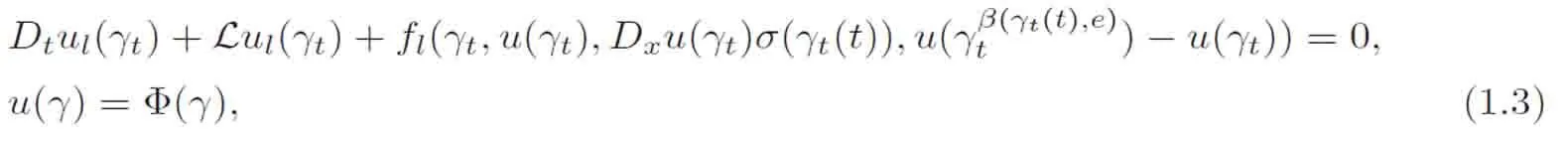
where the derivative is the Dupire’s path derivative(see Section 2.1).More speci fically,the path-function u(t,X(s)0≤s≤t):=Y(t,ω)is the unique-solution to the path-dependent PIDEs(1.3).We refer to Buckdahn-Pardoux[3]for the Markovian case when both Φ and f are functions of the forward di ff usion.The results of this paper non-trivially generalize the ones of[3](see also[1])for the path-dependent situation.
The paper is organized as follows.In Section 2,we present some existing results in the theory of functional Itô’s formula and BSDEs that we will use in this paper.In Section 3,we state the nonlinear Feynman-Kac formula for the “discrete functional” form.Then,in Subsections 4.1–4.2,we first establish some estimates and regularity results for the solution to BSDEs with path.Finally,in Subsection 4.3,we obtain our main results,i.e.,Theorems 4.4 and 4.5,which provide a one to one correspondence between BSDEs and the path-dependent PIDEs.
When the coefficients of BSDE are only Lipschitz functions,we usually can not obtain the smooth results given in this paper,and therefore a new type of viscosity solutions is required.In the Brownian motion case,we refer to[20]for the corresponding comparison theorem.Moreover,[8]introduced a di ff erent stochastic approach to derive a maximum principle for semilinear pathdependent partial differential equations.For a recent account and development of this theory,we refer the readers to[9–10].
2 Preliminaries
2.1 Functional Itô’s formula
The following notations are mainly from Dupire[7].
Let T>0 be fixed.For each t ∈ [0,T],we denote by Λtthe set of c`adl`ag Rd-valued functions on[0,t].For each γ ∈ ΛT,the value of γ at time s ∈ [0,T]is denoted by γ(s).Thus γ = γ(s)0≤s≤Tis a c`adl`ag process on[0,T]and its value at time s is γ(s).The path of γ upto time t is denoted by γt,i.e., γt= γ(s)0≤s≤t∈ Λt.Denote We sometimes speci fically write
γt= γ(s)0≤s≤t=(γ(s)0≤s to indicate the terminal position γ(t)of γt,which often plays a special role in this framework.For each γt∈ Λ and x ∈ Rd,we denote by γt(s)the value of γtat s ∈ [0,t]and:=(γt(s)0≤s Now consider the function u of path,i.e.,u:ΛR.This function u=u(γt)γt∈Λcan also be regarded as a family of real valued functions u(γt)=u(t,γt(s)0≤s≤t)=u(t,γt(s)0≤s We also denote u(γxt):=u(t,γt(s)0≤s We introduce the distance on Λ.Let〈·,·〉and|·|denote the inner product and the norm in Rd.For each 0 ≤ t≤≤ T and γt,t∈ Λ,we denote It is obvious that Λtis a Banach space with respect to‖ ·‖.Since Λ is not a linear space,d∞is not a norm. Definition 2.1(Continuous) A function u:ΛR is said to be Λ-continuous at γt∈ Λ,if for any ε >0,there exists δ>0 such that for eacht∈ Λ with d∞(γtt)< δ,we have|u(γt)− u(γt)|< ε.u is said to be Λ-continuous if it is Λ-continuous at each γt∈ Λ. Remark 2.1In our framework,we often regard u()as a function of t,γtand x,i.e.,u()=u(t,γt(s)0≤s Definition 2.2Given u:ΛR and γt∈ Λ,if there exists p ∈ Rd,such that then we say that u is(vertically)differentiable at γtand denote Dxu(γt)=p.u is said to be vertically differentiable in Λ if Dxu(γt)exists for each γt∈ Λ.We can similarly define the Hessian Dxxu(γt).It is an S(d)-valued function defined on Λ,where S(d)is the space of all d×d symmetric matrices. For each γt∈ Λ,we denote It is clear that γt,s∈ Λs. Definition 2.3For a given γt∈ Λ,if we have then we say that u(γt)is(horizontally)differentiable in t at γtand denote Dtu(γt)=a.u is said to be horizontally differentiable in Λ if Dtu(γt)exists for each γt∈ Λ. Definition 2.4define Cj,k(Λ)as the set of functions u defined on Λ,which are j times horizontally and k times vertically differentiable in Λ,such that all these derivatives are Λ-continuous. Definition 2.5Function u is said to have the horizontal local Lipschitz property if and only if Definition 2.6u is said to be inif u ∈ C1,2(Λ)and for ϕ =u,Dtu,Dxu,Dxxu,we have where C and k are some constants depending only on ϕ. Example 2.1If u(γt)=f(t,γt(t))with f ∈ C1,1([0,T[×R),then Dtu(γt)= ∂tf(t,γt(t)), Dxu(γt)= ∂xf(t,γt(t)),which are the classic derivatives.In general,these derivatives also satisfy the classic properties:linearity,the product rule and the chain rule. The functional Itô formula for continuous martingale was firstly obtained by Dupire[7],and then generalized by Cont and Fournié[4]to more general formulation. Theorem 2.1Let(Ω,F,(Ft)t∈[0,T],P)be a probability space.X is a semimartingale and u is in(Λ).If Dxu has the horizontal local Lipschitz property,then for any t∈ [0,T[: Remark 2.2If u∈(Λ),the horizontal local Lipschitz property for Dxu does not hold in general. In this paper,we will use the following functional Itô formula. Theorem 2.2Let(Ω,F,(Ft)t∈[0,T],P)be a probability space.X=M+A is a semimartingale,where M is a continuous local martingale and A is a finite variation process.If u∈then for any t∈ [0,T[, We give the sketch of proof of Theorem 2.2,which is essentially from Cont and Fournié[4]. ProofWithout loss of generality,we assume that X and |ΔX(s)|are bounded.Otherwise,for each p,denote τp:=inf{s ≥ 0:|X(s)|≥ p orand consider a process Xτp. Let us introduce a sequence of random subdivisions of[0,t],and define the following sequence of stopping times: Then sup{|X(u)−tends to 0 as n → ∞.We set Recall that u∈and (note that(56)also converges to 0 in[4]),and then using the same method as in[4],one can get which completes the proof. 2.2 BSDEs Let(Ω,F,P)be a completed probability space.The filtration(Ft)0≤t≤Tis generated by the following two mutually independent stochastic processes defined on(Ω,F,P),and augmented by all P-null sets: (1)A d-dimensional standard Wiener process{B(t)}t≥0. (2)A Poisson random measure μ on R+× E,where E:=Rd{0}is equipped with its Borel f i eld E,with a compensator ν(dt,de)=dtλ(de),such that{([0,t]×A)=(μ−ν)([0,t]×A)}t≥0is a martingale for all A ∈ E satisfying λ(A)< ∞.λ is assumed to be a σ- finite measure on(E,E)satisfying It is also a right continuous filtration. Remark 2.3We assume that the L´evy measure λ satis fies(2.3)instead of<∞,and then the jump-di ff usion process X in the sequel satisfies the conditions of the functional Itô formula(2.2). We also introduce the following spaces of processes which will be used frequently in the sequel: Let us consider a function f:Ω×Rn×Rn×d×L2(E,E,λ;Rn)Rn,which is P-measurable for each(y,z,k)∈ Rn×Rn×d×L2(E,E,λ;Rn).For the function f,we will make the following assumptions: (A1)f(·,0,0,0)∈ H2(0,T;Rn). (A2)There exists a constant C ≥ 0,such that for all t∈[0,T],y,y∈Rn,z,z∈Rn×d,k,k ∈ L2(E,E,λ;Rn),P-a.s. The following result on BSDEs with jumps is by now well-known,and for its proof the readers are referred to Lemma 2.4 in[22]or Theorem 2.1 in[1]. Lemma 2.1Let f satisfy the conditions(A1)–(A2),and then for each ξ∈ L2(FT;Rn),the BSDE with jump has a unique adapted solution (Y(t),Z(t),K(t))0≤t≤T∈ B2. We have the following comparison theorem for solutions to(2.4)(see Proposition 2.6 in[1]). Lemma 2.2(Comparison Theorem)Let h:Ω×[0,T]×R×Rd×RR be P×B×Bd×B-measurable and satisfy that for any y,y∈R,z,∈Rd,q,∈R,and t∈[0,T],there exists some constant K>0,such that (i) (ii) (iii)qh(t,y,z,q)is non-decreasing. Furthermore,let l:Ω × [0,T]× ER be P × B(E)measurable and satisfy 0≤l(t,e)≤K(1∧|e|), e∈E. Set Given ξ1,ξ2∈ L2(FT;R),we have that f2satisfies(A1)–(A2).Denote by(Y1,Z1,K1)and(Y2,Z2,K2)the solutions to the BSDE with the data(ξ1,f1)and(ξ2,f2),respectively.Then we have the following result:If ξ1≥ ξ2and f1(t,y,z,k) ≥ f2(t,y,z,k),a.s.,a.e.for any(y,z,k)∈R×Rd×L2(E,E,λ;R),then Y1(t)≥ Y2(t),a.s.,for all t∈ [0,T]. For each i∈{1,2},the drivers giare given by gi(s,y,z,u)=f(s,y,z,u)+ϕi(s), ds×dP-a.e., where ϕi∈ H2(0,T;Rn)and f satisfies the assumptions(A1)–(A2).The following lemma is due to Buckdahn-Pardoux[3]. Lemma 2.3Let ξi∈ L2(FT;Rn).Then the solution(Yi,Zi,Ki)to the BSDE(2.4)with the data(ξi,gi)satisfies the following estimate:For any p ≥ 2,there exists Cpdepending on T and p,such that Remark 2.4Note that in Lemma 2.3,we assume only that ξi∈ L2(FT)and the process ϕi∈H2(t,T;Rn)to guarantee the solvability of the BSDE.However,if p≥2 and the right-hand side is∞,the estimate obviously holds. Cnwill denote respectively the set of functions of class Cnfrom Rpinto Rq,the set of those functions of class Cn(Rp;Rq)whose partial derivatives of order less than or equal to n are bounded Lipschitz continuous functions,and the set of those functions of class Cn(Rp;Rq),which together with all their partial derivatives of order less than or equal to n are in Cl,lip(Rp;Rq),where Cl,lip(Rp;Rq)is the space of all Rq-valued continuous functions ϕ defined on Rp,such that Here C and k are some constants depending only on ϕ. In this section,we shall study the nonlinear Feynman-Kac formula when the BSDEs with jumps are of the “discrete functional” form.We refer to[12]for the BSDEs case(see also[14–15]).Consider the following(discrete)functional-type BSDEs defined on an arbitrary interval[t,T]⊂[0,T]:For each s∈[t,T], where 0=t0≤ t1≤ ···≤ tN=T is a given partition on[0,T].We denote any solution to(3.1),whenever it exists,by(Xt,x,Yt,x,Zt,x,Kt,x)to indicate its dependence on the initial data(t,x).For convenience,for any x=(x1,···,xN)∈ RNdand k=1,···,N,set In particular,denote Then(3.1)can be rewritten as For each k=N,N − 1,···,1,consider a sequence of semilinear PIDEs with parameters,defined recursively in a “backward” manner as follows:First, fixx(N−1)as a parameter,and define Next,for each k=N,N − 1,···,1,we fixx(k−1)as a parameter,and consider the following PIDEs:For each(t,x)∈ [tk−1,tk)×Rd, For ϕ∈C2(Rd;R),the operator L is given by Now suppose that all PIDEs have classical solutions which are denoted by uki,i=1,···,n,k=N,N − 1,···,1.For convenience,set Finally,for t∈ [0,T],if t∈ (tk−1,tk],k=N,N −1,···,2 or t∈ [t0,t1],denote Then,we have the following nonlinear Feynman-Kac formula. Theorem 3.1Assume that all PIDEs in(3.2)have classical solutions whose derivatives are of polynomial growth.Then,the process(Y,Z,K)defined by(3.3)solves BSDE(3.1)on[0,T]. ProofWe shall check the case t∈ [tN−1,tN],and the other cases can be argued in the same way. Applying the Itô’s formula and by the Definition of uN,we deduce that From(3.2),we obtain that(Y,Z,K)solves the BSDE on(tN−1,T].Note that at t=tN−1, From the Definitions of the functions uN−1and vN−1,we can similarly prove that(Y,Z,K)solves the BSDE on(tN−2,tN−1].Continuing this way for N steps,the proof is completed. We should note that various assumptions can be made to guarantee the existence and uniqueness of the classical solution to the system of PIDEs,as well as the adapted solution to the BSDE(3.1).In particular,by Theorem 4.1 in[3],we have the following lemma. Lemma 3.1Let b∈β :Rd× ERdbe measurable.For all e∈ E,β(·,e)∈there exists a constant K ≥ 0,such that For each i∈ {1,···,N},fi(s,x1,···,xN,y,z,k)∈ C0,0,2([0,T]×R(N−1)d×Rd×Rn×Rn×d×L2(E,E,λ;Rn);Rn)and Moreover,for each s ∈ [0,T],fi(s,x1,···,xN,y,z,k)∈(R(N−1)d×Rd×Rn×Rn×d×L2(E,E,λ;Rn);Rn).Functions ∂yfi(t,·), ∂zfi(t,·), ∂kfi(t,·)are bounded Lipschitz functions,and so are their derivatives of order one with respect to xN,y,z,k.Furthermore,all their Lipschitz coefficients are uniformly bounded.If for each i ∈ {1,···,N},gi(x1,···,xN) ∈and then all PDEs in(3.2)have classical solutions. Note that when we say the(Frechet)derivative w.r.t k is bounded,we mean that its norm in L2(E,E,λ;Rn)is bounded.In the sequel,we always assume that b,σ,β satisfy the above conditions. Remark 3.1From(3.3),the process Z is left continuous with right limit(LCRL for short).Since the Brownian motion is continuous,we can also define Z by Z(t)in(3.3). In this section,we will generalize the nonlinear Feynman-Kac formula for the path-dependent situation.The following directional derivatives will be used frequently in the sequel. Definition 4.1Suppose that Φ is an Rn-valued function on ΛT.Then Φ is said to be in C2(ΛT;Rn),if it is twice continuously Frechet differentiable at each γ ∈ ΛT. Φ is said to be inand there exist some constants C ≥ 0 and k ≥ 0 depending only on Φ such that for each s≤ t∈ [0,T],γ,∈ ΛT, with Ψ =Analogously,for each t∈ [0,T],we can define Remark 4.1Since ΛTis a Banach space with respect to the uniform norm,for each γ,bounded linear map,andis a ΛT× ΛTRnbounded linear map.Example 4.1If Φ(γ)=ϕ(γ(s))ds for some ϕ ∈then Φ ∈ In the rest of this paper,we shall make use of the following assumptions on the generator f and the terminal Φ of our BSDE. (H1) Φ is an Rn-valued function on ΛT.Moreover,Φ ∈with the Lipschitz coefficients C and k. (H2)f(γt,y,z,k)is an Rn-valued continuous function on Λ × Rn× Rn×d×L2(E,E,λ;Rn).For any γt∈ Λ,(y,z,k)f(γt,y,z,k)is in,(y,z,k),,are in,(y,z,k)→is a Lispchitz function and(y,z,k),,z,k),are in Cl,lip(Rn×Rn×d×L2(E,E,λ;Rn);Rn)for any(y,z,k),γtf(γt,y,z,k)is in, γt,,are inγt,,,,,are in Cl,lip(Λt;Rn).They are all continuous in t,and so are their derivatives.Moreover,all their Lipschitz coefficients are uniformly bounded. (H3)f(γt,y,z)=(t,γt(t),y,z,k),where For each t∈ [0,T],(t,·)∈(Rd×Rn×Rn×d×L2(E,E,λ;Rn);Rn)and ∂yf(t,·),∂zf(t,·),∂k(t,·)are in Cb,lip(Rd×Rn×Rn×d×L2(E,E,λ;Rn);Rn),and so are their derivatives of order one with respect to x,y,z,k.Moreover,all their Lipschitz coefficients are uniformly bounded. It is obvious that the assumption(H3)implies the assumption(H2). Assume that(H1)–(H2)hold.For any γt∈ Λ,(Yγt(s),Zγt(s),Kγt(s))t≤s≤Tis the solution to the following BSDE: where By Lemma 2.1,for each γt∈ Λ,(4.1)has a unique solution(Yγt,Zγt,Kγt)∈ B2and Yγt(t)defines a deterministic mapping from Λ to Rn. We next establish higher-order moment estimates for the solution of the BSDE(4.1).Without loss of generality,the Lipschitz coefficients of f are also denoted by C and k.For convenience,define Yγt(s),Zγt(s),Kγt(s)for any t,s ∈ [0,T],γt∈ Λ by Yγt(s)=Yγt(s ∨ t),while Zγt(s)=0 and Kγt(s)=0 for s From Lemma 2.3 and Proposition 3.5 in[21],we deduce the following theorem. Theorem 4.1For any p≥2,there exist some constants Cp>0 and q>0 depending on C,T,k,p,such that for any t,t∈ [0,T],γt,t∈ Λ,h,∈ R{0}, whereis an orthonormal basis of Rd. Now we define Theorem 4.2For each γt∈ Λ,has a version which is a.e.in C0,2([0,T]× Rd).In particular,Dxu(γt),Dxxu(γt)exist and u ∈ ProofTo simplify presentation,we shall only prove the case when n=d=1,as the higher-dimensional case can be treated in the same way without substantial difficulty. Since for each h,∈R{0}and k,∈R, using the Kolmogorov’s criterion,the existence of a continuous derivative ofwith respect to x follows from the above estimates,as so is the existence of mean-square derivatives ofand with respect to x,which is mean square continuous in x.Denote them by(DxYγt,DxZγt,DxKγt). By the Definition of vertical derivatives,Dxu(γt)exists.We shall prove u(γt)is Λ-continuous.Putting s=t in the BSDE(4.1)and taking expectation,we get For each γt,∈ Λ with t≥ t, where we have used the assumptions(H1)–(H2)in the last inequality.Applying Theorem 4.1,we can find some constant C1depending only on C,k and T so that By a similar argument,we have u ∈ By Lemma 4.1,we conclude that‖Kγt(s)‖Eare in Lp(FT)for any p>0.Since(DxYγt,DxZγt,DxKγt)is the solution to the following linearized BSDE: the existence of a continuous second-order partial derivative ofwith respect to x is proved in a similar fashion and this completes the proof. In[3],when the BSDE is the state-dependent case,i.e.,f=f(t,γ(t),y,z,k)and Φ =ϕ(γ(T)),it is shown that Z,K and Y are connected in the following sense under appropriate assumptions: In this section,we extend this result to the path-dependent case.Indeed,we have below a formula relating Z,K with Y. Theorem 4.3Under assumptions(H1)–(H2),for each fixed γt∈ Λ,the processes(Zγt(s),have the following a.s.left continuous version given by A direct consequence of Theorem 4.3 is the following result. Lemma 4.1For each p≥2,there exist some constants Cpand q depending only on C,T,k and p,such that and Now we give the proof of Theorem 4.3. Proof of Theorem 4.3To simplify presentation,we shall only prove the case when n=d=1,as the higher-dimensional case can be treated in the same way without substantial difficulty.We will suppress the superscript γtfor notational convenience. Step 1For each s ∈ [0,T)and a positive integer m,we introduce a mappingΛsΛs: wherek=0,1,···,m.Denoteand then there exists some constant C,such that By Lemma 2.3,we also haveConsequently,u(Xs)=Y(s). Step 2Denote Φm():= Φ(γm())and fm(s,y,z,k):=f(γm(s),y,z,k).Then for each m,there exist some functions ϕmdefined on Λt×Rm×dand ψmdefined on[t,T]×Λt×Rm×d×Rn×Rn×d×L2(E,E,λ;R),such that Indeed,set Recalling the assumptions(H1)–(H2),we obtain thatwhere In particular, Furthermore,for each fixedtand i∈ {1,···,m},ψim(s,t,x1,···,xm,y,z,k)∈ C0,0,2([t,T]×R(m−1)d×Rd×Rn×Rn×d×L2(E,E,λ;Rn);Rn),where For each Functionsandare bounded Lipschitz functions,and so are their derivatives of order one with respect to xm,y,z,k. Now consider the following BSDEs,for any≥ t,∈ Λ, DenoteBy Theorems 3.1,4.2 and Lemma 3.1(see also Lemma 3.10 in[21]),we can get u(m)(γt)∈Moreover,for each s∈ [t,T],s∈ Λ,and l∈ {1,···,n}, In particular,for each s∈[t,T], Denote by C0a constant that depends only on C,T and k,which is allowed to change from line to line.From Lemma 2.3,for each∈ Λ, Moreover,we also deduce that Thus,it holds that By Lemma 2.3,which implies that Step 3From BSDE(4.1),we see that the compensated processes of jumps of Y are given by Since Y(s)=u(Xs),we also have the representation We claim that the function tis left continuous for each γt∈ Λ and x ∈ Rd.Recalling the proof of Theorem 4.2,for each γt∈ Λ and x ∈ Rd,there exists some constant C1depending on γt,x,such that Thus the integrand in(4.6)is predictable,and from the uniqueness of the integral representation,we obtain the desired result. We now establish the relationship between our BSDE and the following path-dependent parabolic integro-differential equation: where u=(u1,···,un):ΛRnis a function on Λ and We immediately obtain the following theorem. Theorem 4.4Assume that assumptions(H1)–(H2)hold,and let u ∈be a solution to(4.7).Then for each γt∈ Λ,we have u(γt)=Yγt(t),where(Yγt(s),Zγt(s),Kγt(s))t≤s≤Tis the unique solution to the BSDE(4.1).Consequently,the path-dependent PDE(4.7)has at most one-solution. ProofWe again suppress the superscript γtfor notational convenience.Applying thefunctional It’s formula(2.2)to u(Xs)on s ∈ [t,T),for each l∈ {1,···,n}, Since u solves PDE(4.7),we have that Recalling u(XT)=Φ(XT)and u∈(Y(s),Z(s),K(s))=(u(Xs),Dxu(Xs−)σ(X(s−)),is the unique solution to the BSDE(4.1).In particular,u(γt)=Yγt(t).This completes the proof. By Theorem 4.4 and Lemma 2.2,we have the following comparison theorem of pathdependent PIDE. Lemma 4.2Let n=1.We assume that f=fi,Φ = Φi,i=1,2 satisfy the same assumptions as in Lemma 2.2 and Theorem 4.4.Moreover, (i)f1(γt,y,z,k)≤ f2(γt,y,z,k),for each(γt,y,z,k)∈ Λ × R × Rd× L2(E,E,λ;R); (ii) Φ1(γT)≤ Φ2(γT)for each γT∈ ΛT. If ui∈is the solution to(4.7)associated with(f,Φ)=(fi,Φi),i=1,2,respectively,then for each γt∈ Λ,u1(γt)≤ u2(γt). We are now in a position to prove the converse to the above result. Theorem 4.5Under assumptions(H1)–(H2),the function u defined in(4.2)is the unique-solution to the path-dependent PIDE(4.7). ProofLet δ>0 be such that t+δ≤ T.We again suppress the superscript γtfor notational convenience.Hence By(4.8)and the proof of Theorem 4.3,we obtain a.s.(choosing a subsequence if necessary) Moreover,for each∈ Λdwith, Now applying theformula,we deduce that Thus by(4.5),(4.9)and the dominated convergence theorem,we have where Recalling(4.4),we can find some constant c depending only on C,T,γtand k so that Hence Finally,taking expectation on both sides of(4.10)yields Thus u∈and it satisfies(4.7). Remark 4.2We make assumptions(H1)–(H2).Then is the unique solution to the BSDE(2.4). Remark 4.3In the case that Φ(γ)= ϕ(γ(T))for some ϕ ∈and f satisfies(H3),the above result is the nonlinear Feynman-Kac formula,which is given by Buckdahn-Pardoux[3]. Example 4.2Suppose n=d=1 and where f satis fies(H3).In this case,the BSDE(4.1)has the explicit solution as follows: Given Φ :ΛTR, for some ϕ ∈(R),then for each γt∈ Λt, Using the classic Feynman-Kac formula,we deduce that is the solution to the following parabolic integro-differential equation: Thus By the de finitions of horizontal derivatives and vertical derivatives,we have Consequently, which satis fies(4.7). AcknowledgementsThe author would like to thank Prof.Peng,S.for his careful reading,helpful discussions and suggestions.The author also thanks the editor and two anonymous referees for their helpful suggestions. [1]Barles,G.,Buckdahn,R.and Pardoux,E.,Backward stochastic differential equations and integral-partial differential equations,Stochastics Stochastics Rep.,60,1997,57–83. [2]Bismut,J.M.,Conjugate convex functions in optimal stochastic control,J.Math.Anal.Appl.,44,1973,384–404. [3]Buckdahn,R.and Pardoux E.,BSDEs with jumps and associated integro-partial differential equations,preprint. [4]Cont,R.and Fournié,D.A.,Change of variable formulas for non-anticipative functionals on path space,J.Funct.Anal.,259(4),2010,1043–1072. [5]Cont,R.and Fournié,D.A.,A functional extension of the Itô formula,C.R.Math.Acad.Sci.Paris.,348(1),2010,57–61. [6]Cont,R.and Fournié,D.A.,Functional Itô calculus and stochastic integral representation of martingales,Ann.Probab.,41(1),2013,109–133. [7]Dupire,B.,Functional Itô calculus,Portfolio Research Paper 2009-04,Bloomberg. [8]Ekren,I.,Keller,C.,Touzi,N.and Zhang,J.,On viscosity solutions of path dependent PDEs,Ann.Probab.,42(1),2014,204–236. [9]Ekren,I.,Touzi,N.and Zhang,J.,Viscosity solutions of fully nonlinear parabolic path dependent PDEs:Part I.arXiv:1210.0006 [10]Ekren,I.,Touzi,N.and Zhang,J.,Viscosity solutions of fully nonlinear parabolic path dependent PDEs:Part II.arXiv:1210.0007 [11]El Karoui,N.,Peng,S.and Quenez,M.C.,Backward stochastic differential equation in finance,Math.Finance,7(1),1997,1–71. [12]Hu,Y.and Ma,J.,Nonlinear Feynman-Kac formula and discrete-functional-type BSDEs with continuous coefficients,Stochastic Process.Appl.,112(1),2004,23–51. [13]Ma,J.and Yong,J.,Forward-backward stochastic differential equations and their applications,Lecture Notes in Mathematics,1702,Springer-Verlag,Berlin,1999. [14]Ma,J.and Zhang,J.,Representation theorems for backward SDEs,Ann.Appl.Probab.,12(4),2002,1390–1418. [15]Ma,J.and Zhang,J.,Path regularity for solutions of backward stochastic differential equations,Probab.Theory Related Fields.,122(2),2002,163–190. [16]Pardoux,E.and Peng,S.,Adapted solutions of backward stochastic equations,Systems Control Lett.,14,1990,55–61. [17]Pardoux,E.and Peng,S.,Backward stochastic differential equations and quasilinear parabolic partial differential equations,Stochastic Partial Differential Equations and Their Applications,B.L.Rozuvskii and R.B.Sowers(eds.),Lect.Notes Control Inf.Sci.,Vol.176,Springer-Verlag,Berlin,Heidelberg,New York,1992,200–217. [18]Peng,S.,Probabilistic interpretation for systems of quasilinear parabolic partial differential equation,Stochastics Stochastics Rep.,37,1991,61–74. [19]Peng,S.,A nonlinear Feynman-Kac formula and applications,Control Theory,Stochastic Analysis and Applications(Hangzhou,1991),World Sci.Publ.,River Edge,NJ,1992,173–184. [20]Peng,S.,Note on viscosity solution of path-dependent PDE and G-martingales.arXiv:1106.1144 [21]Peng,S.and Wang,F.,BSDE,path-dependent PDE and nonlinear Feynman-Kac Formula.arXiv:1108.4317 [22]Tang,S.and Li,X.,Necessary conditions for optimal control of stochastic systems with random jumps,SIAM J.Control Optim.,32(5),1994,1447–1475.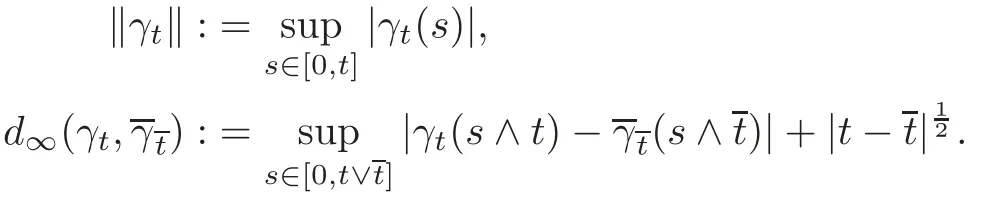
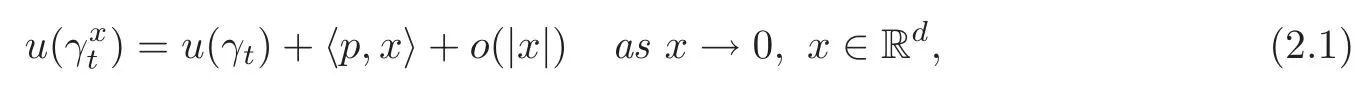
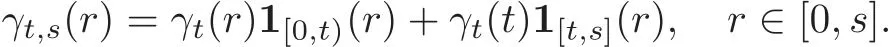


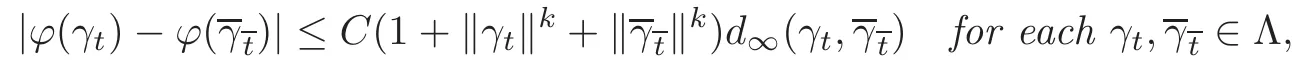
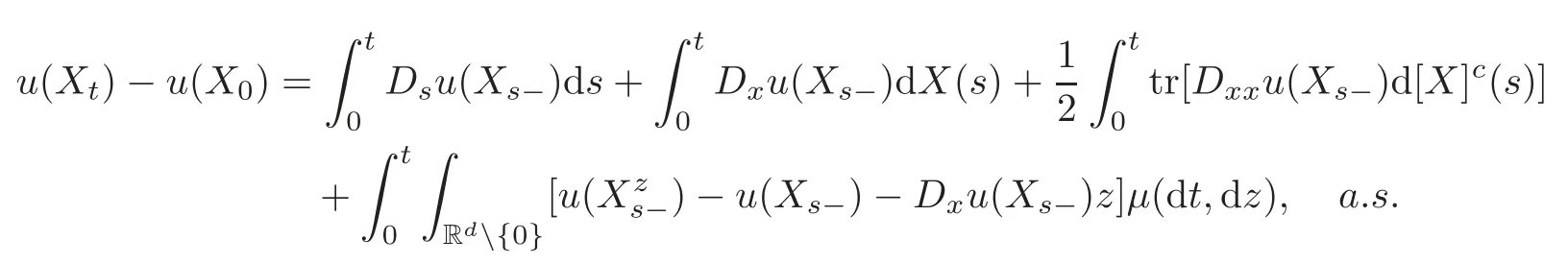

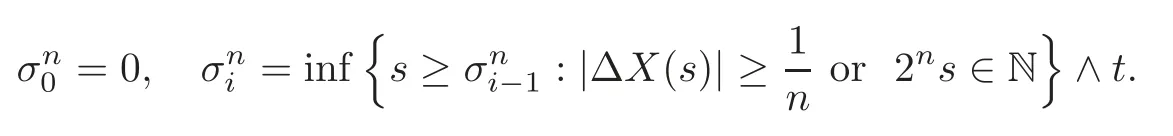
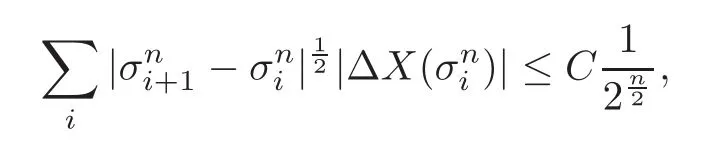
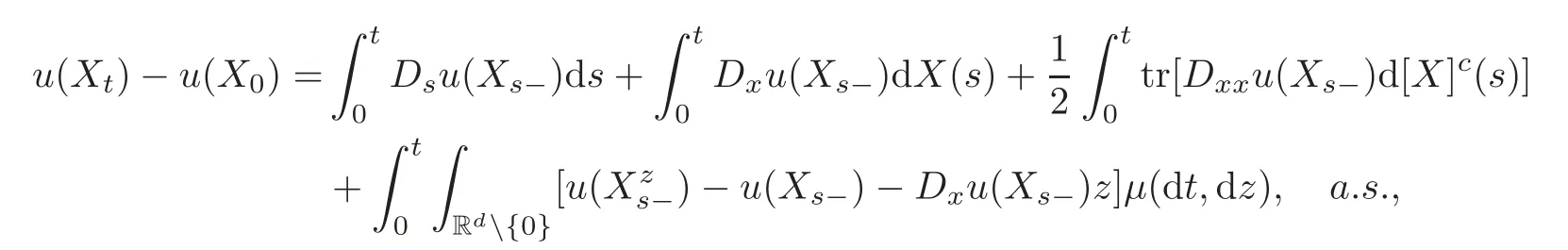


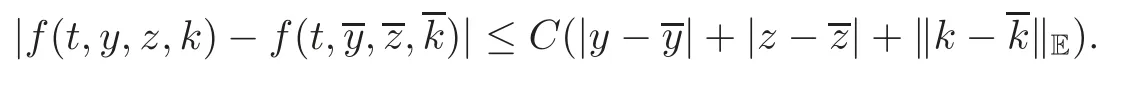
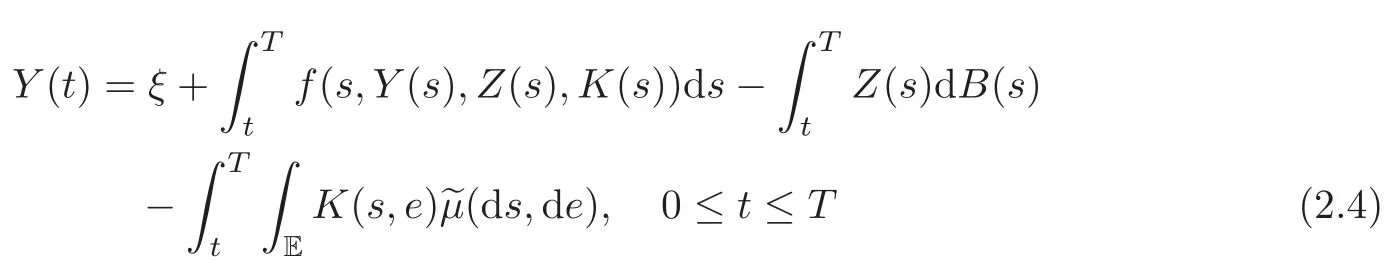

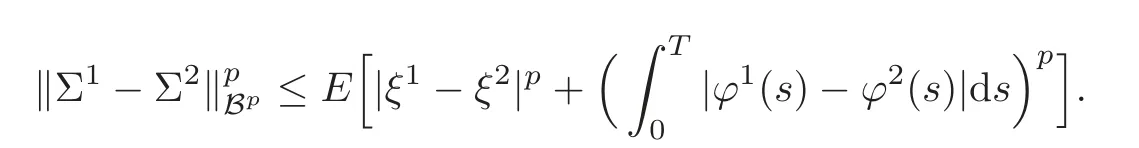
3 Nonlinear Feynman-Kac Formula for “Discrete Functional” Form
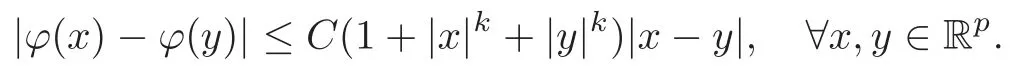
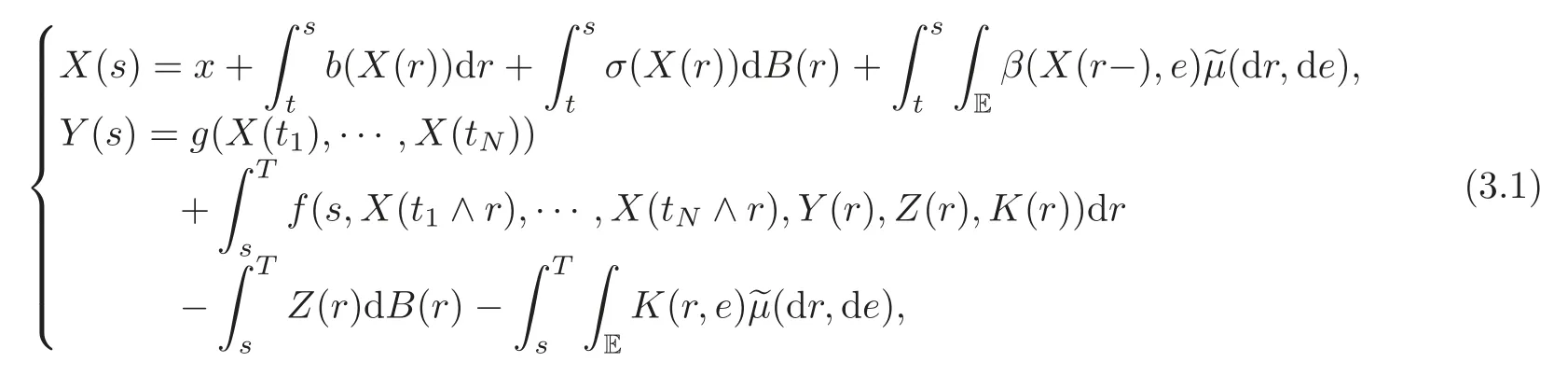
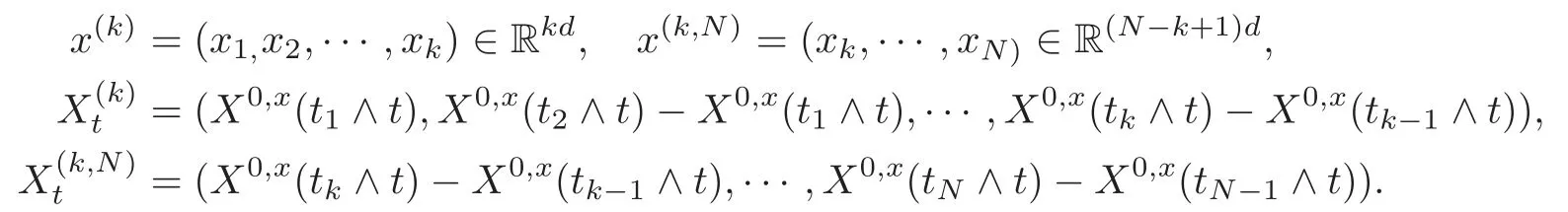
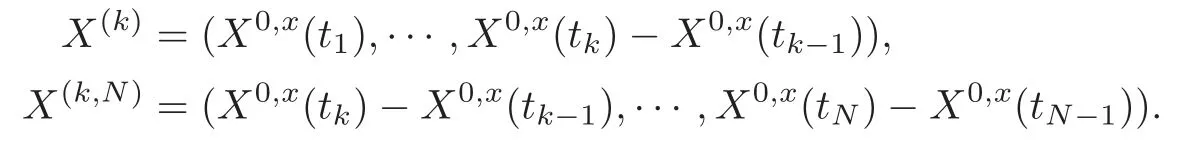
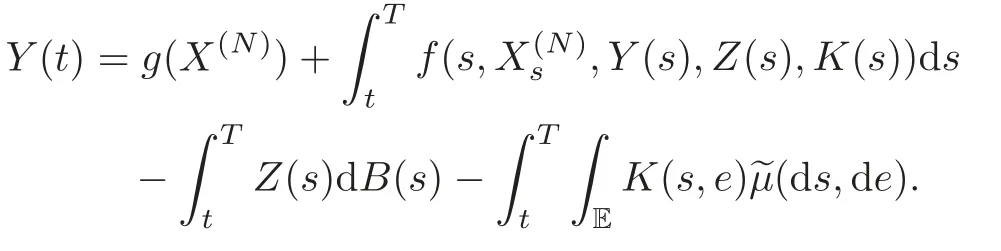



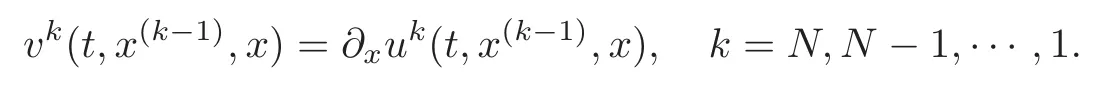
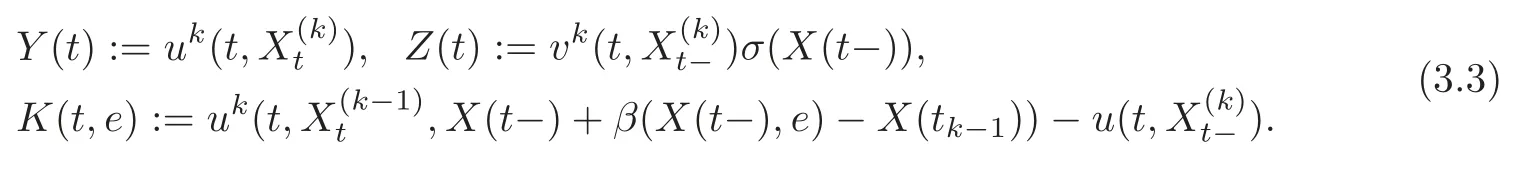
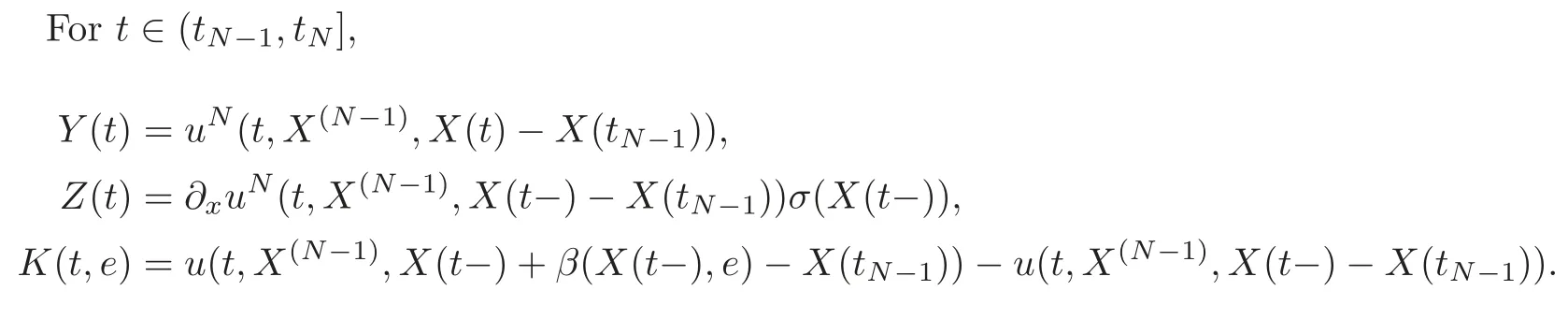
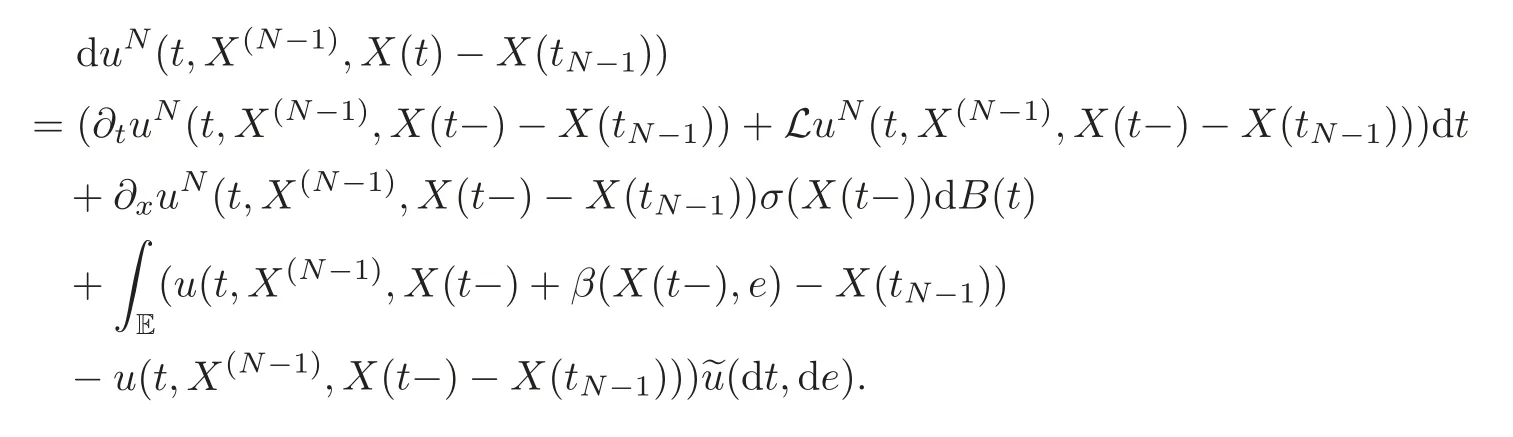




4 Nonlinear Feynman-Kac Formula for Functional Form
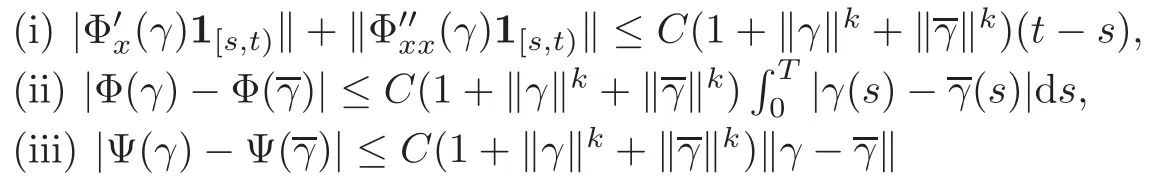
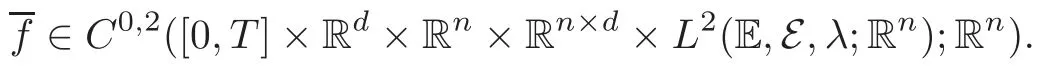
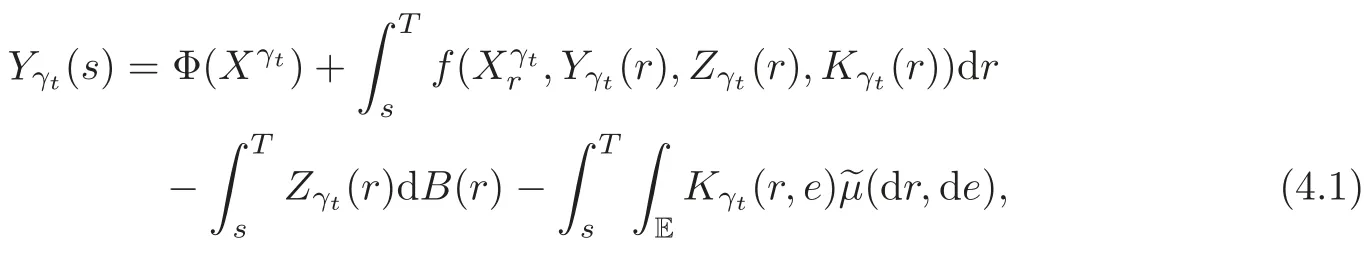

4.1 Property of solution to the BSDE with jumps
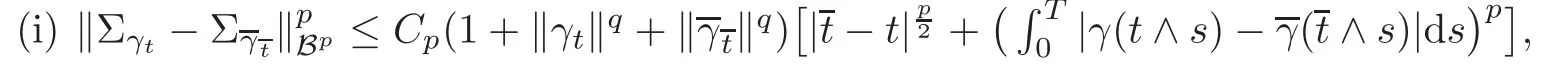


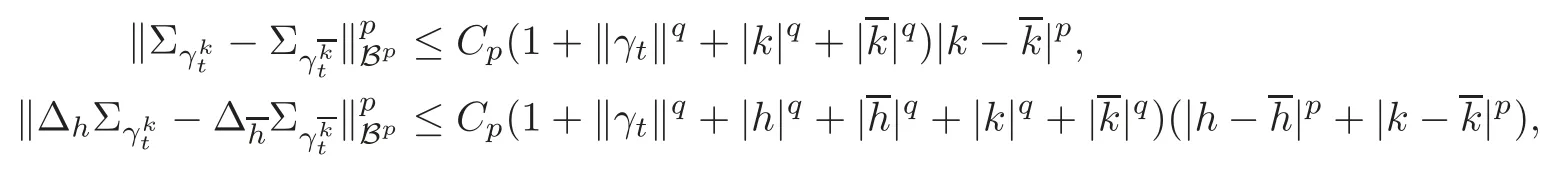
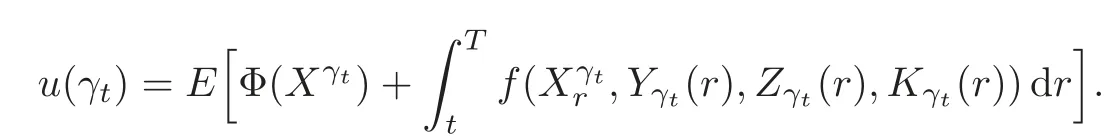
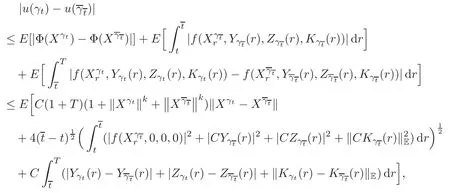


4.2 Path regularity of processes Z and K

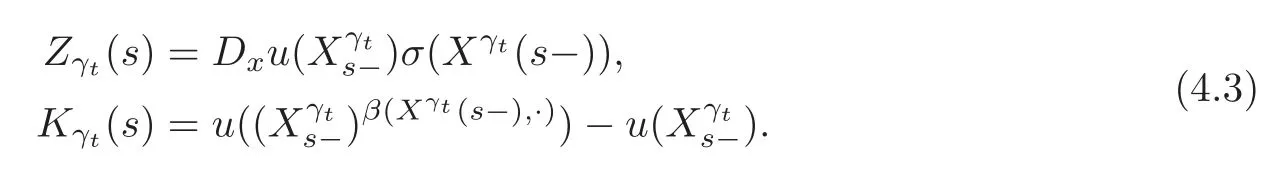

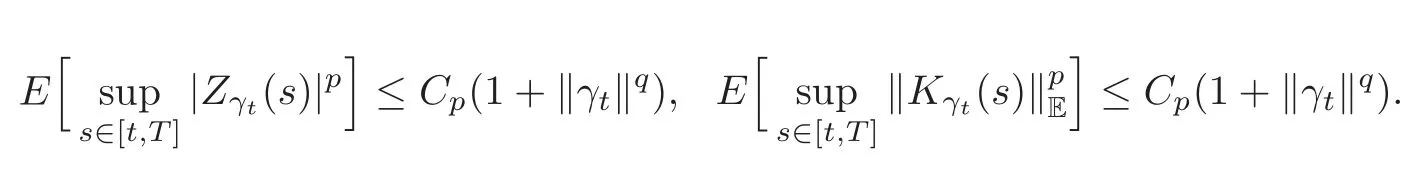

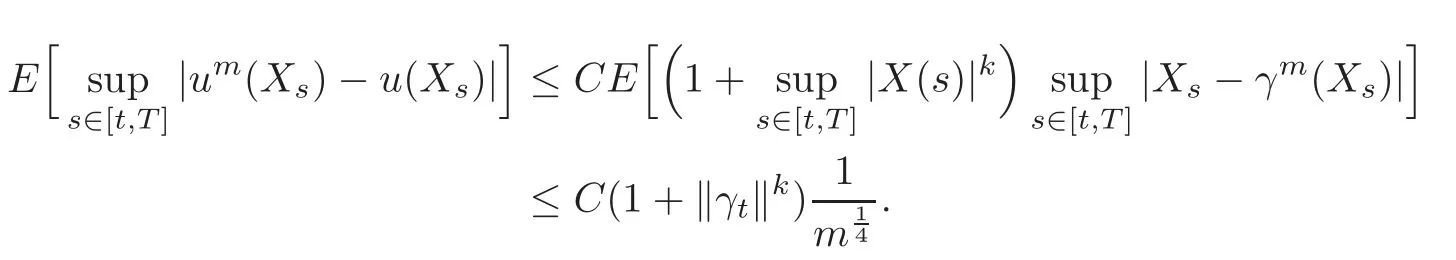
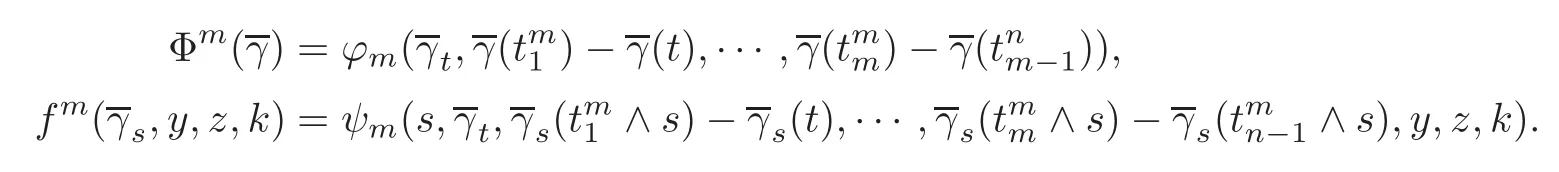
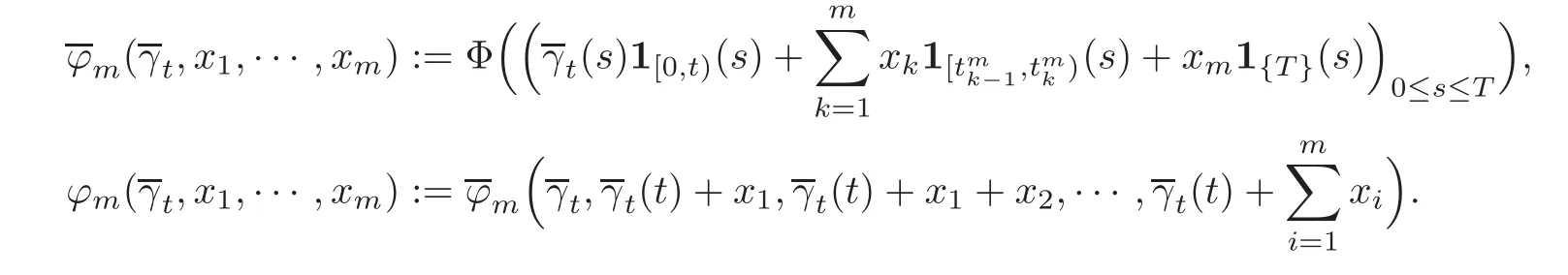


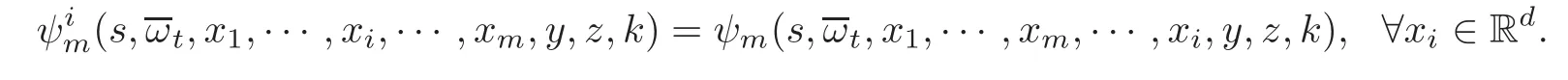
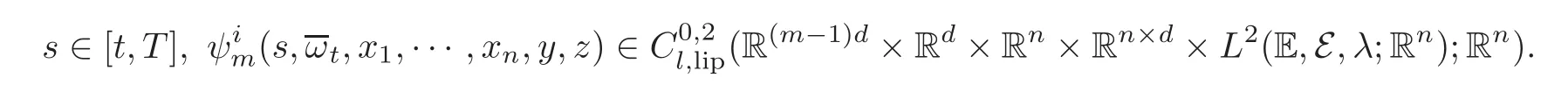

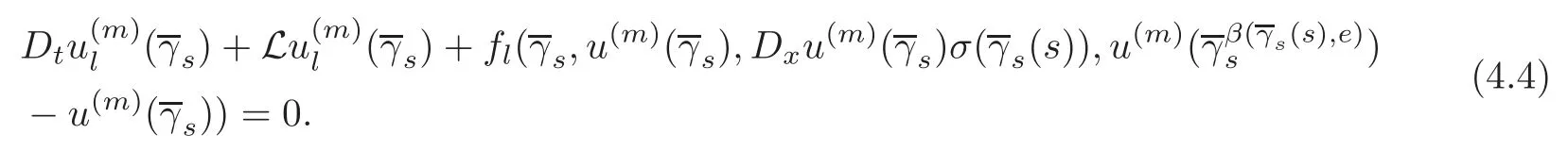
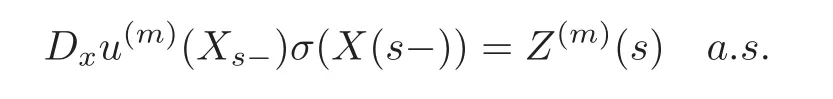
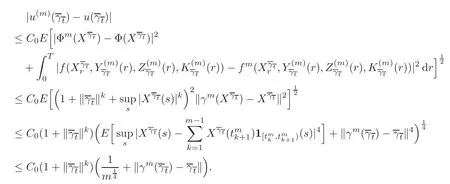




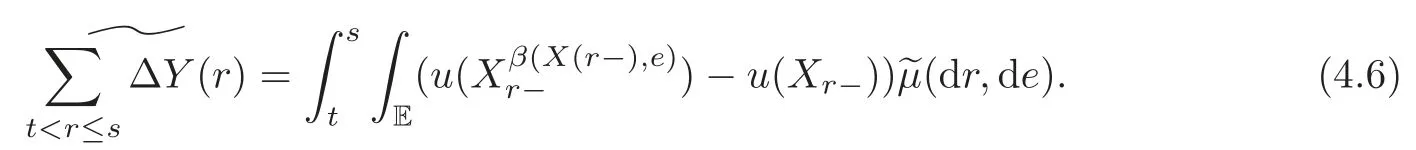
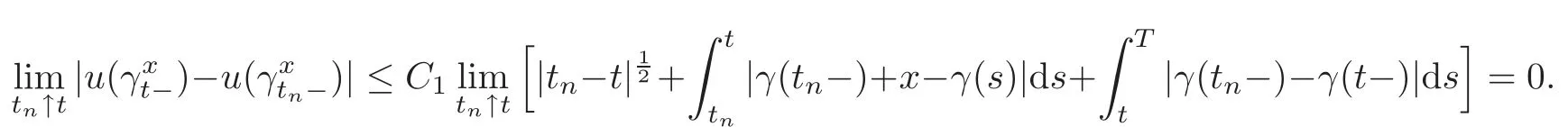
4.3 Path-dependent parabolic integro-differential equations


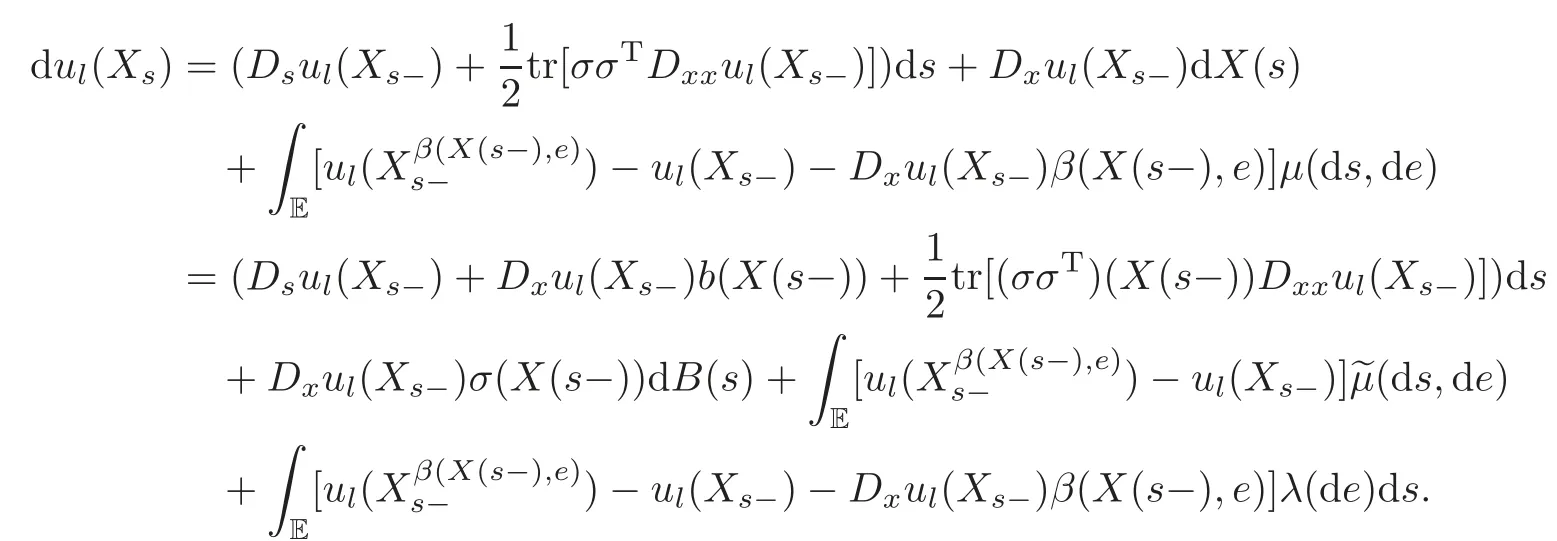

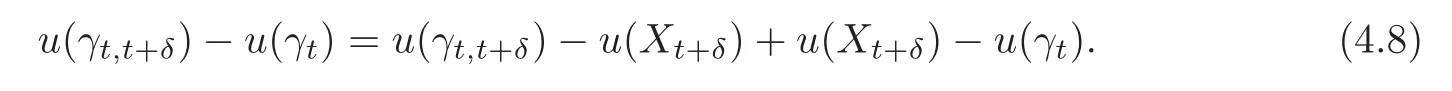



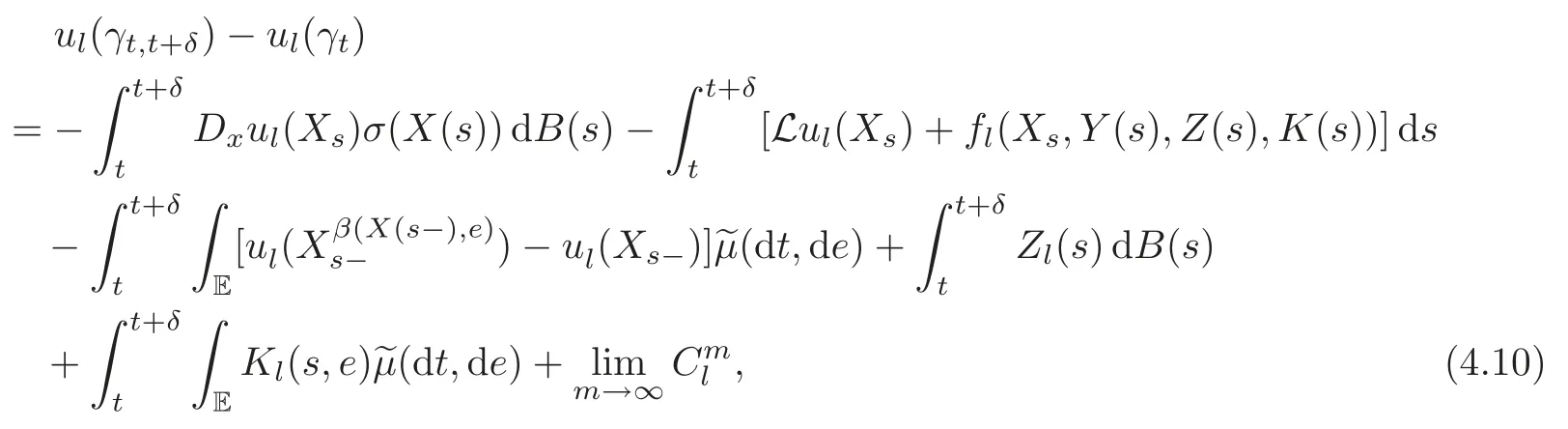

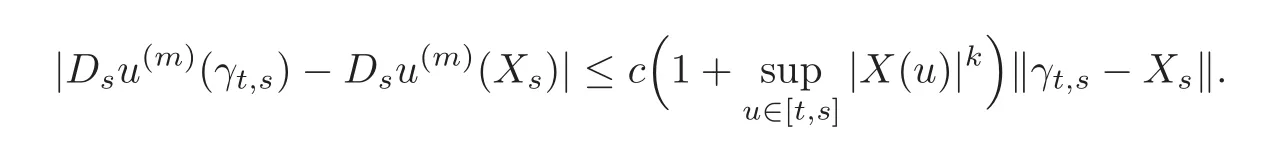

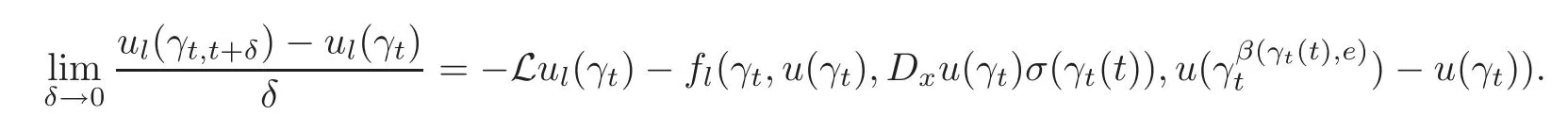
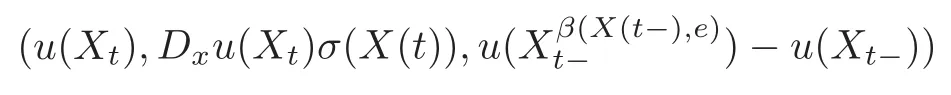
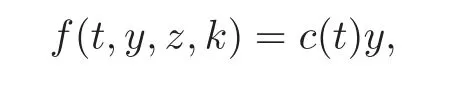

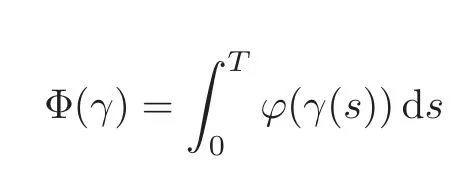
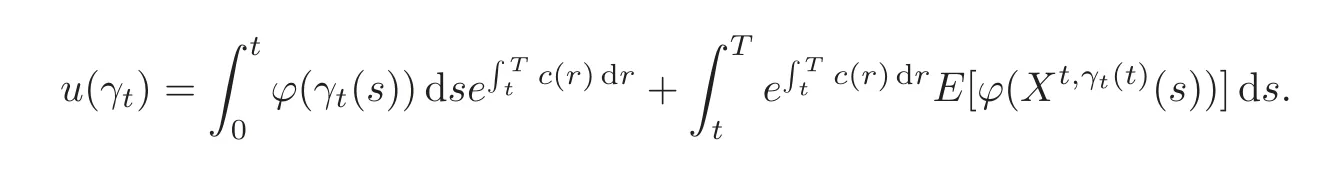
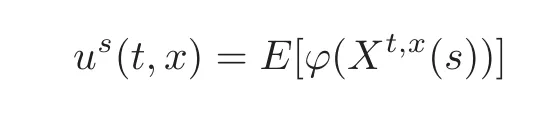
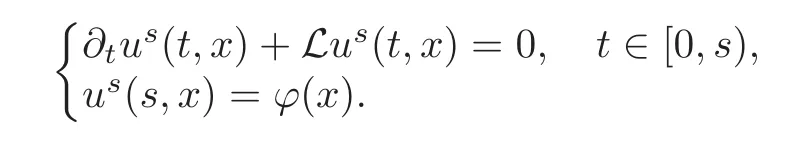

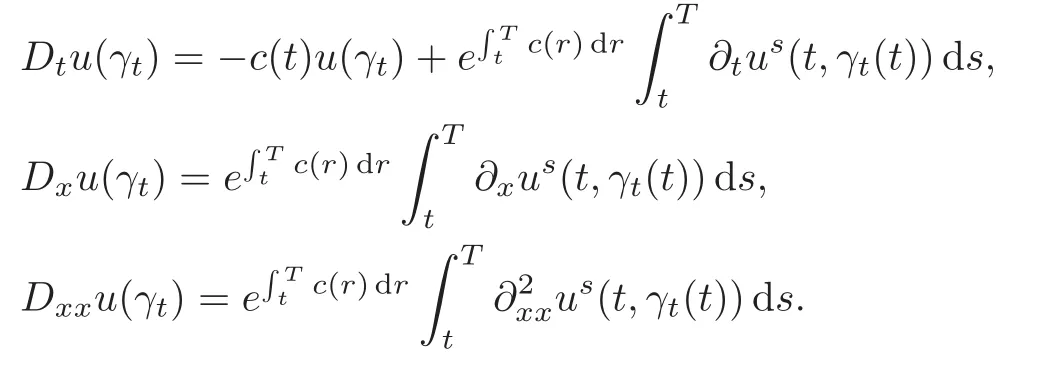
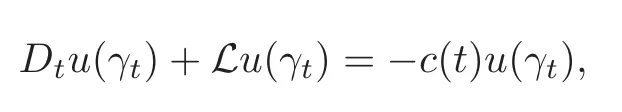
 Chinese Annals of Mathematics,Series B2015年4期
Chinese Annals of Mathematics,Series B2015年4期
