On the Dedekind Sums and Two-Term Exponential Sums∗

Di HAN Tingting WANG

1 Introduction

Let q be a natural number and h an integer prime to q.The classical Dedekind sums

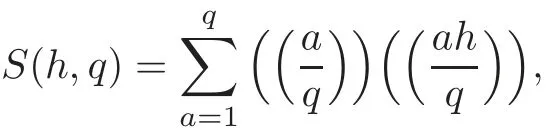
where

describes the behaviour of the logarithm of the eta-function(see[10–11])under modular transformations.About the arithmetical properties of S(h,q),one can find them in[1,6,9,13–14].

Recently,the second author and Zhang[12]studied the computational problem of the mean value

and obtained several interesting computational formulae for it,where the two-term exponential sums C(m,n,k,h;q)are defined as follows:

e(y)=e2πiyand≡ 1 mod p.Some results related to C(m,n,k,h;q)can be found in references[2–5].

In this paper as a note of[12],we consider the hybrid mean value

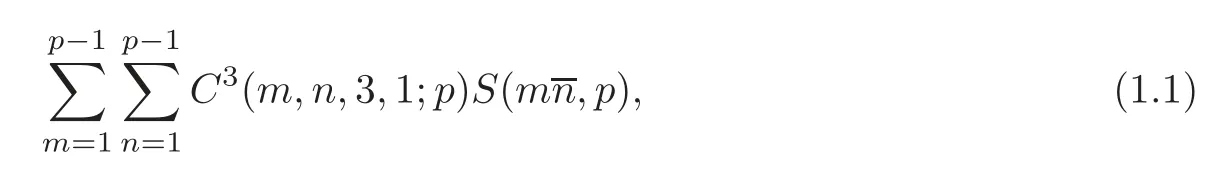
and then use the analytic method to give an exact computational formula for(1.1).That is,we shall prove the following theorem.

Theorem 1.1For any odd prime p>3,we have the computational formulae:

(A)If p≡1 mod 4,then

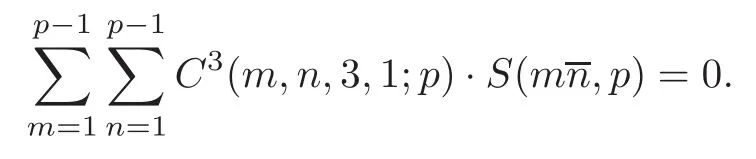
(B)If p=12k+11,and u0is the solution of the congruent equation u3≡−4 mod p,then

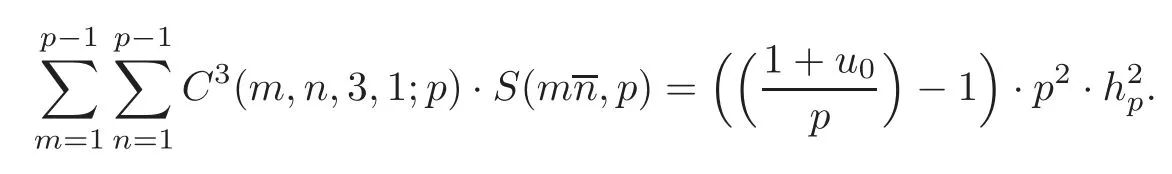
(C)If p=12k+7,and the congruent equation u3≡−4 mod p has no solution,then

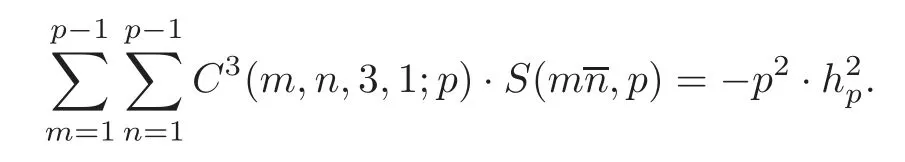
(D)If p=12k+7,and the congruent equation u3≡ −4 mod p has three integer solutions u1,u2and u3,then

where () denotes the Legendre’s symbol,and hpdenotes the class number of the quadratic field

It is clear from this theorem that we may immediately deduce the following corollary.

Corollary 1.1Let p=12k+7 be an odd prime such that 4 is not a cubic residue mod p,and then we have the identity

For general integers q≥3 and k≥4,whether there exists an exact computational formula for the mean value

and

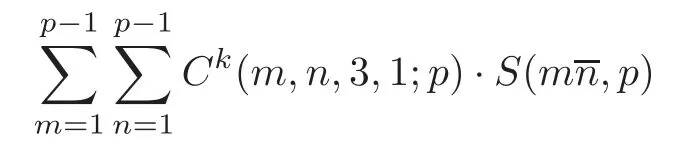
is an open problem,where p is an odd prime.

2 Several Lemmas

In this section,we shall give several lemmas,which are necessary in the proof of our theorem.First we have the following lemma.

Lemma 2.1Let p>3 be a prime.Then for any integer n with(n,p)=1,we have the identity

wheredenotes the Legendre’s symbol.

ProofSee Lemma 1 of[12].

Lemma 2.2Let p>3 be a prime with p≡3 mod 4,and then we have the identities:

(U)If p=12k+11,and u0satis fies the congruence u3≡−4 mod p,then

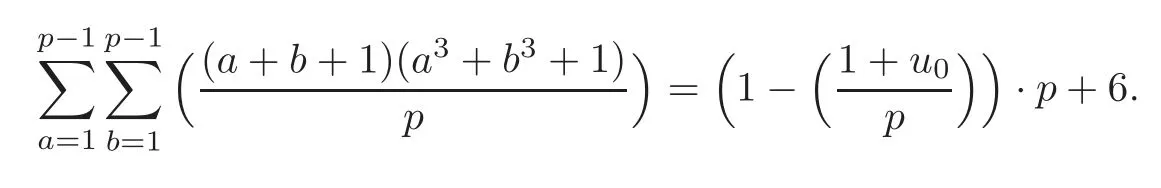
(V)If p=12k+7,and the congruence u3≡−4 mod p has no solution,then

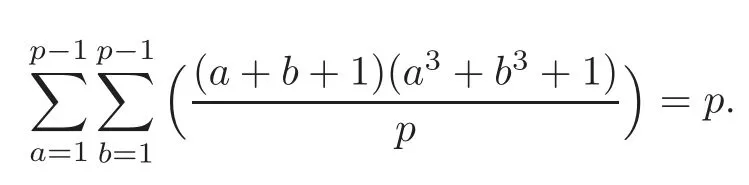
(W)If p=12k+7 and the congruence u3≡ −4 mod p has three solutions u1,u2and u3,then

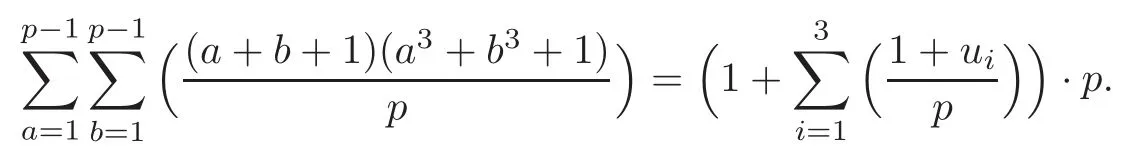
ProofFirst let a+b=u,and then from the properties of the Legendre’s symbol,we have the identity

Now for prime p>3,from Lemma 2.1 we have the identity

If p=12k+11,then=1 and(3,p−1)=1.This time,if u0passes through a residue system mod p,thenalso passes through the residue system,so there exists one and only one integer 1≤u0≤p−1 such that the congruence≡−4 mod p or 4≡0 mod p.For other u,we have

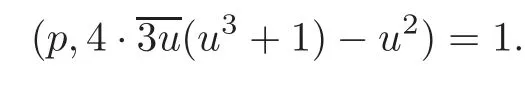
By Lemma 2.1,noting that

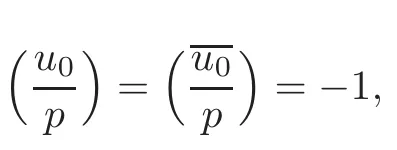
we have

So if p=12k+11,then combining(2.1)–(2.3),we have

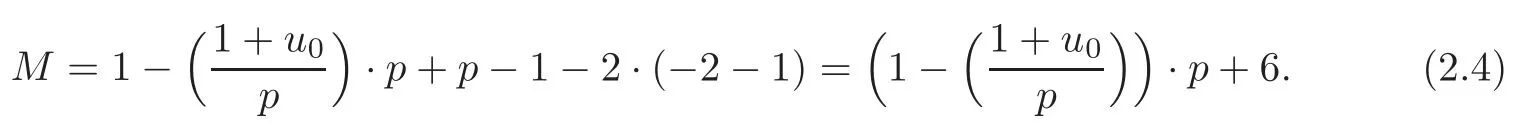
If p=12k+7,then= −1 and(3,p−1)=3.So the number of the solutions of the congruence equation u3≡−4 mod p is 0 or 3.

(I)If the equation u3≡−4 mod p has no solutions,then from the method of proving(2.4),we have

(II)If the equation u3≡ −4 mod p has three solutions:u1,u2and u3.Then=−1,i=1,2,3.From the method of proving(2.4),we have

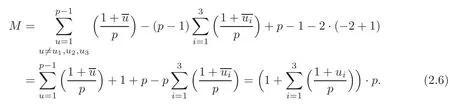
Now Lemma 2.2 follows from(2.4)–(2.6).

Lemma 2.3Let p>3 be a prime,and χ be any odd character mod p.Then we have the identities:

(a)If p≡1 mod 4,then

(b)If p=12k+11,and u0satisfies the congruent equation u3≡−4 mod p,then

(c)If p=12k+7,and the congruent equation u3≡−4 mod p has no solutions,then

(d)If p=12k+7,and the congruent equation u3≡ −4 mod p has three solutions u1,u2and u3,then

ProofFrom the Definition and the properties of the Gauss sums τ(χ),we have

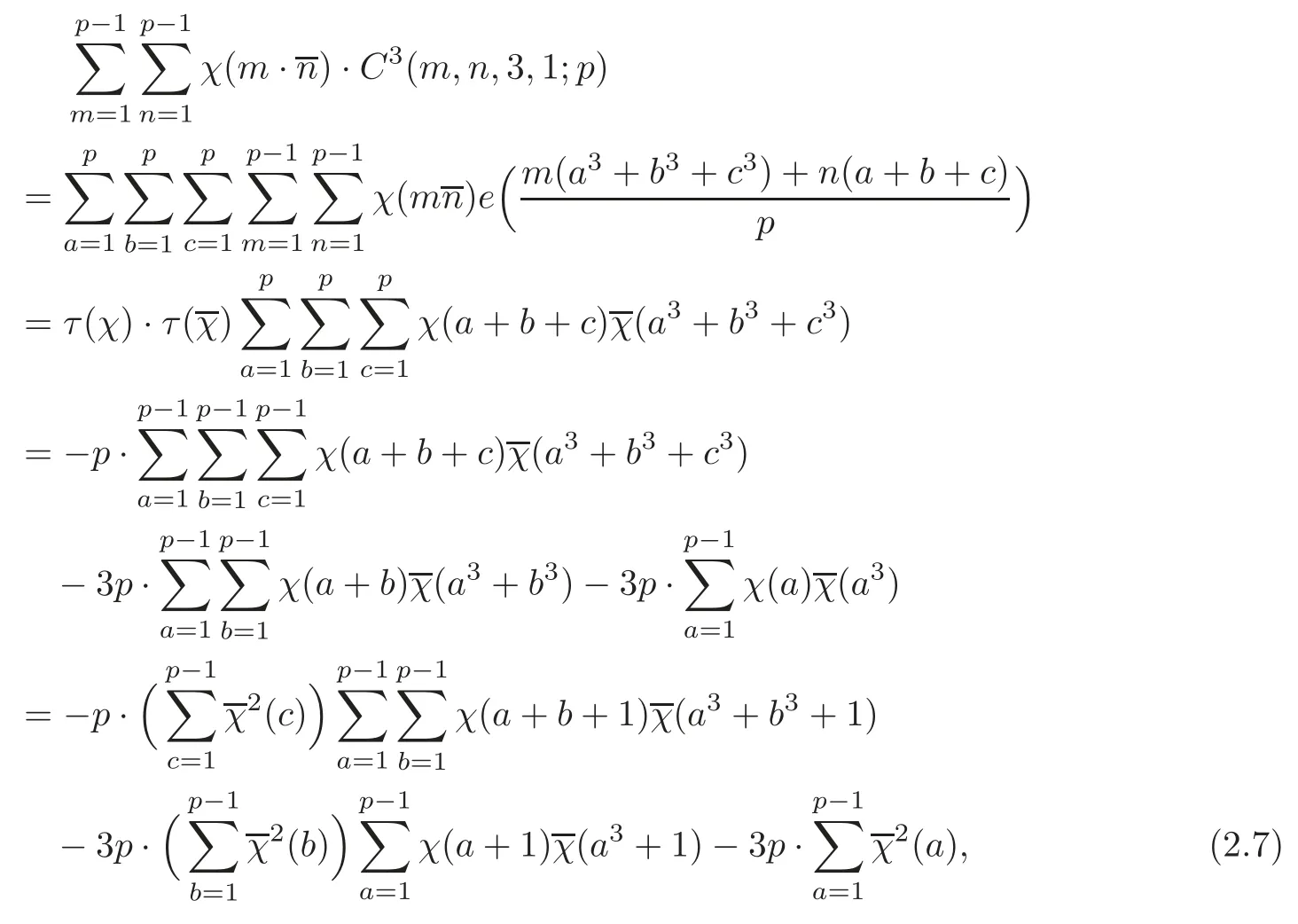
where we have used the fact that τ(χ)·τ()= −p,if χ is an odd character mod p.

If p ≡ 1 mod 4,then for any odd character χ mod p,2is a non-principal character mod p.So we have

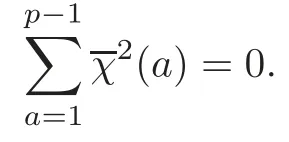
Therefore,from(2.7)we can deduce that

If p ≡ 3 mod 4,then for any non-real odd character χ mod p,2is a non-principal character mod p.So we also have

If χ is the Legendre’s symbol,then χ2is the principal character mod p,and

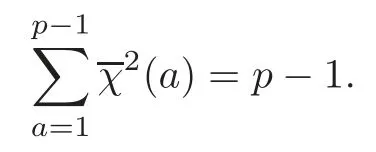
Therefore,from(2.2),(2.7)and(U)of Lemma 2.2,we can deduce that if p=12k+11,and u0satisfies the congruent equation u3≡−4 mod p,then

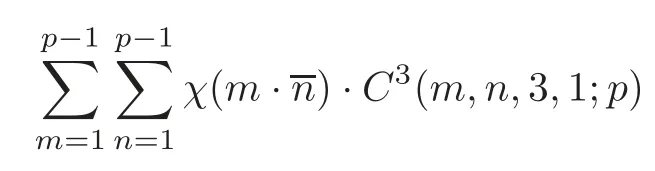
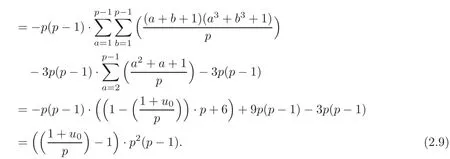
If p=12k+7,and the congruent equation u3≡−4 mod p has no solutions,then from(2.2),(2.7)and(V)of Lemma 2.2,we can deduce that

If p=12k+7,and the congruent equation u3≡ −4 mod p has three solutions u1,u2and u3,then from(2.2),(2.7)and(W)of Lemma 2.2,we can deduce that

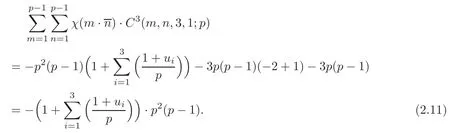
Now Lemma 2.3 follows from(2.8)–(2.11).

Lemma 2.4Let p=12k+7 be an odd prime such that the congruent equation u3≡−4 mod p has three integer solutions u1,u2and u3.Then we have the identity

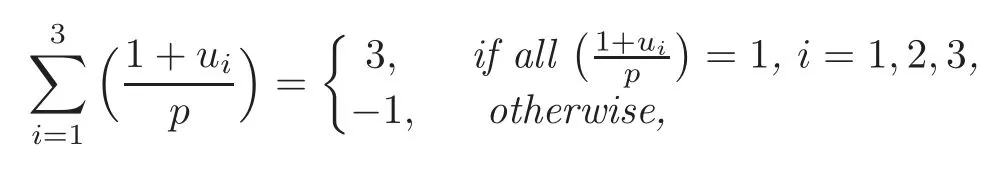
where ()denotes the Legendre’s symbol.

ProofSince u1,u2and u3are the three integer solutions of the congruent equation u3≡−4 mod p,from the properties of the polynomial congruence,we have

(u−u1)(u−u2)(u−u3)≡0 mod p

or

u3−u2(u1+u2+u3)+u(u1u2+u2u3+u3u1)−u1u2u3≡0 mod p.

Comparing this formula with u3+4≡0 mod p,we have the congruences

u1+u2+u3≡0 mod p, u1u2u3≡−4 mod p

and

u1u2+u2u3+u3u1≡0 mod p.

Then using these three congruences we have

From this identity and noting thatwe may immediately deduce

This proves Lemma 2.4.

Lemma 2.5Let q>2 be an integer,and then for any integer a with(a,q)=1,we have the identity

where L(1,χ)denotes the Dirichlet L-function corresponding to the character χ mod d.

ProofSee Lemma 2 of[14].

3 Proof of Theorem 1.1

In this section,we shall complete the proof of our theorem.By Lemma 2.5,we have

If p≡1 mod 4,then from(3.1),the Definition of C(m,n,3,1;p)and(a)of Lemma 2.3,we have

If p=12k+11,and u0is the solution of the congruent equation u3≡ −4 mod p,then noting that L(1,χ2)=(see[7,p.50]),from(3.1),the Definition of C(m,n,3,1;p)and(b)ofLemma 2.3,we have

If p=12k+7,and the congruent equation u3≡ −4 mod p has no solutions,then from(3.1),the Definition of C(m,n,3,1;p)and(c)of Lemma 2.3,we have

If p=12k+7,and the congruent equation u3≡−4 mod p has three solutions u1,u2and u3,then from(3.1),Lemma 2.4,the Definition of C(m,n,3,1;p)and(d)of Lemma 2.3,we have

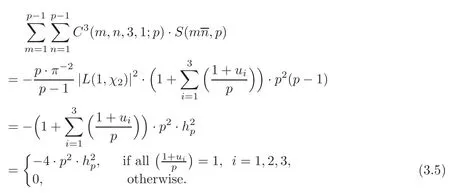
Now our conclusion follows from(3.2)–(3.5).This completes the proof of our theorem.

AcknowledgementThe authors would like to thank the referees for their very helpful and detailed comments,which have signi ficantly improved the presentation of this paper.

[1]Apostol,T.M.,Modular Functions and Dirichlet Series in Number Theory,Springer-Verlag,New York,1976.

[2]Cochrane,T.and Zheng,Z.,Upper bounds on a two-term exponential sums,Sci.in China(Series A),44,2001,1003–1015.

[3]Cochrane,T.,Exponential sums modulo prime powers,Acta Arithmetica,101,2002,131–149.

[4]Cochrane,T.and Pinner,C.,A further re finement of Mordell’s bound on exponential sums,Acta Arithmetica,116,2005,35–41.

[5]Cochrane,T.and Pinner,C.,Using Stepanov’s method for exponential sums involving rational functions,Journal of Number Theory,116,2006,270–292.

[6]Conrey,J.B.,Fransen,E.,Klein,R.and Scott,C.,Mean values of Dedekind sums,Journal of Number Theory,56,1996,214–226.

[7]Davenport,H.,Multiplicative Number Theory,Springer-Verlag,New York,1980.

[8]Hua,L.K.,Introduction to Number Theory,Science Press,Beijing,1979.

[9]Jia,C.,On the mean value of Dedekind sums,Journal of Number Theory,87,2001,173–188.

[10]Rademacher,H.,On the transformation of log η(τ),J.Indian Math.Soc.,19,1955,25–30.

[11]Rademacher,H.and Grosswald,E.,Dedekind Sums,Carus Mathematical Monographs,Math.Assoc.Amer.,Washington D.C.,1972.

[12]Wang,T.and Zhang,W.,On the hybrid mean value of Dedekind sums and two-term exponential sums,Frontiers of Mathematics in China,6,2011,557–563.

[13]Zhang,W.,A note on the mean square value of the Dedekind sums,Acta Mathematica Hungarica,86,2000,275–289.

[14]Zhang,W.,On the mean values of Dedekind sums,Journal de Théorie des Nombres de Bordeaux,8,1996,429–442.