A Result on the Quasi-periodic Solutions of Forced Isochronous Oscillators at Resonance∗

Bin LIU Yingchao TANG

1 Introduction

In this paper,we consider the existence of quasi-periodic solutions and the boundedness of all solutions for forced isochronous oscillators with a repulsive singularity.We also assume that the equation we considered depends on the velocity.

Consider the second-order ordinary differential equation

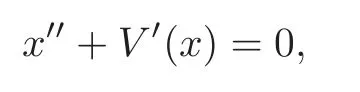
in which the potential functionVis continuous.We callx=0 an isochronous center if

and there is a fixed numberT>0 such that every solution is periodic with periodT.Ifx=0 is an isochronous center,we call the equation above an isochronous system.A typical example of the isochronous system is

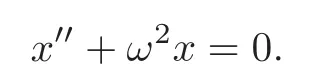
It is easy to see that every solution of this equation is-periodic int.Another important class of isochronous systems is the asymmetric equation

wherex+=max(x,0),x−=x−x+.This is because all solutions are periodic with the periodπ().In the above examples,the equations are both defined on the whole real line.People also consider the system

Obviously,all solutions are 2π-periodic.The di ff erence between this equation and the first two equations is that,this equation is not defined on R,and the potential tends to in finity asx→−1.More information of isochronous centers can be found in[3].

In 1969,Lazer and Leach studied the equation

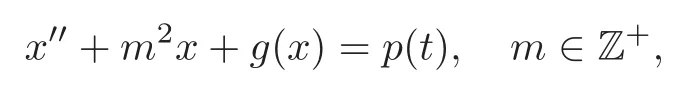
with a 2π-periodic functionp.They showed in[12]that,ifg(±∞)=exists and

then this equation has at least one 2π-periodic solution.The above inequality is called the Lazer-Landesman condition.

Since then,many mathematicians investigated the existence of periodic solutions for the equations

wherepis periodic with period 2π(see[4–5,7–11]and the references therein).In their works,they assumed the functionto be of the form(x)=m2xor(x)=ax+−bx−.So the equation(1.1)can be viewed as a perturbation of an isochronous system.They showed that the type of Lazer-Landesman condition always plays a key role for the existence of periodic solutions.

Bonheure,Fabry and Smets[1]studied the forced isochronous oscillators with jumping nonlinearities and a repulsive singularity.The Lazer-Landesman-type condition is a key assumption to guarantee the existence of periodic solutions in their work.In the following,we brie fly go over their result.

Assume that the functiongis smooth and bounded,and the functionVsatisfies

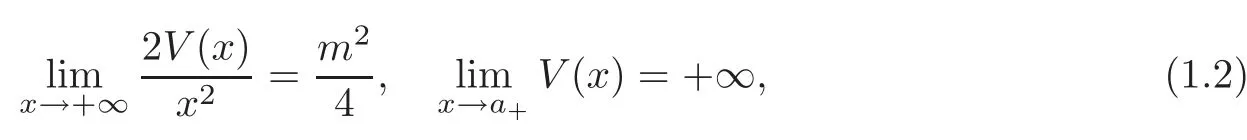
wherem∈Z+,a∈(−∞,0)andVis defined on(a,+∞).We also assume that all solutions of the unperturbed equation

are-periodic,that is,(1.3)is an isochronous oscillator with period.In this case,the equation(1.1)is a bounded perturbation of isochronous oscillators at resonance.The second condition in(1.2)means that the equation(1.3)has a repulsive singularity ata.

Let

Then(1.1)has at least one 2π-periodic solution if there isg0∈[,],which is a regular value ofp∗,and the number of zeros ofp∗−g0in[0,)is di ff erent from 2,where

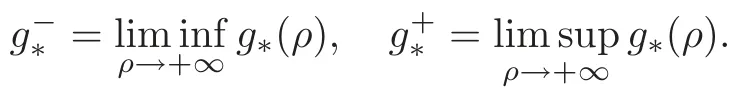
In particular,as a corollary,if the limitexists,then the condition of the Lazer-Landesman type

guarantees the existence of 2π-periodic solutions of(1.1).

In[17],Ortega considered the boundedness of solutions and the existence of quasi-periodic solutions for asymmetric oscillators.Following his result,there are several results(see[14,18–19]and the references therein)on the boundedness of solutions for(1.1).However,in these works,the functionVis globally defined in R.That is,they do not include the case of the oscillators with a singularity.

In[18],Ortega also proved a variant of Moser’s small twist theorem.Under some reasonable assumptions,he showed that aC6small twist area-preserving mapping has invariant curves.Moreover,he used the variant of Moser’s small twist theorem to obtain the boundedness of a piecewise linear equation

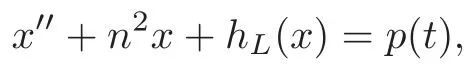
wherep(t)is a 2π-periodic function of classC5,hL(x)is of the following form:

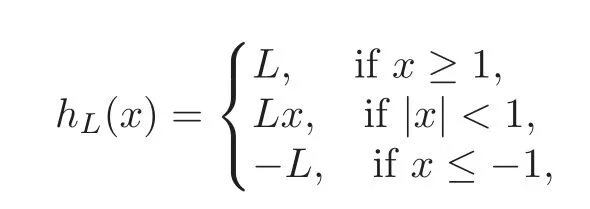
andp(t)satisfies

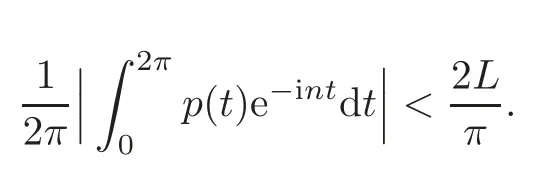
In 2009,Capietto,Dambrosio and Liu[2]studied(1.1)withg(x)=0 and

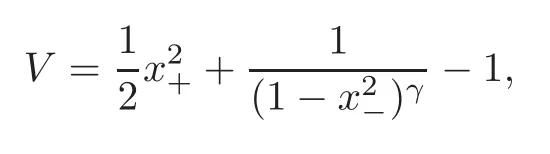
whereγis a positive integer.They showed the boundedness of solutions and the existence of quasi-periodic solutions via Moser’s twist theorem.Here,Vhas a singularity−1.As far as we know,this is the first example of the boundedness of solutions for the equations with singularities.However,this equation is not isochronous.

In[15],Liu showed that,under the condition(1.4)and other regular assumptions onV,gandp,the equation(1.1)has many quasi-periodic solutions and all solutions are bounded.It seems that this is the first result on the existence of quasi-periodic solutions and the boundedness of all solutions for isochronous oscillators with a singularity.

In this paper,we extend the results in[15]to the case of the equation whereedepends on the velocity.More precisely,we study the equation

where the functionsV,gandesatisfy the following assumptions:

(1)The functionVis defined in the interval(−1,+∞)andforx≠0,and the condition(1.2)holds.

(2)The function

is smooth in(−1,∞)and the limitW(x)exists.Furthermore,we assume that the following estimates hold:For each 1≤k≤6,there is a constantc0,such that

(3) The positive functionVis smooth and for 0≤k≤6,

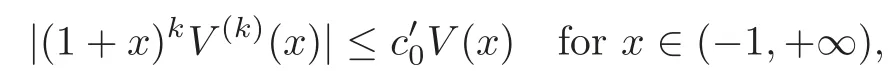
whereis a positive constant.

(4) The functiongis bounded on the interval[−1,+∞)andg(x)>0 forx>0.Moreover,the following equalities hold:

(5) Forx>0,let Φ(x)=V(x)and the function Φ satisfies

for every positive integerk.

(6) There is a constantM>0,such that|e(t,x,y)|≤M,and for 1≤j+i+l≤7,

Furthermore,there exists a function(t),such that

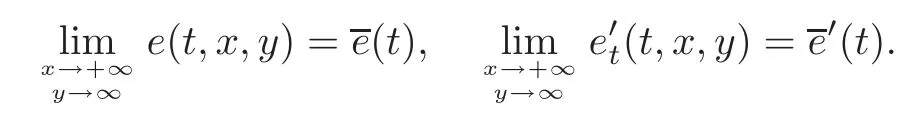
Moreover,the functioneis 2π-periodic int,and

e(−t,x,−y)=e(t,x,y).

Then we have the following theorem.

Theorem 1.1Under the hypotheses(1)–(6)above,for a smooth function e=e(t,x,y),if the Lazer-Landesman-type condition

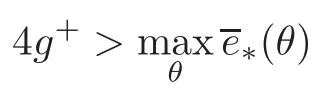
holds,wherethen all solutions of(1.5)are bounded,i.e.,foreach solution x,we have

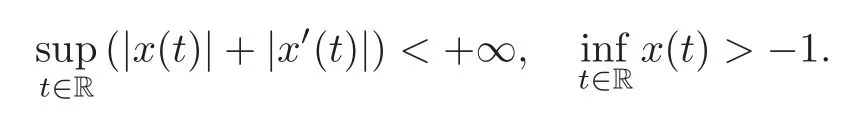
Furthermore,in this case,the equation(1.5)has in finite many quasi-periodic solutions.

The idea for proving our theorem is that,under the hypothesis(1)–(6)of our theorem,we can obtain that the Poincaré map of(1.5)satisfies the assumptions of a variant of Moser’s twist theorem in[16].These conditions are analogous to those in[13].

In the following,for simplicity and brevity,we assume thatm=1,i.e.,the solutions of the equationx″+Vx(x)=0 are 2π-periodic,andm=1 in(1.2)and the assumption(5).The proof of our statements for generalm(the functioneis also 2π-periodic int)can be treated analogously.

The paper is organized as follows.In Section 2,we introduce action and angle variables.After that we state and prove some technical lemmas in Section 3,which are employed in the proof of our main result.In Sections 4–6,we will give an asymptotic expression of the Poincaré map and prove the main result by the twist theorem in[16].

2 Action and Angle Variables

The equation(1.5)can be written in the following form:

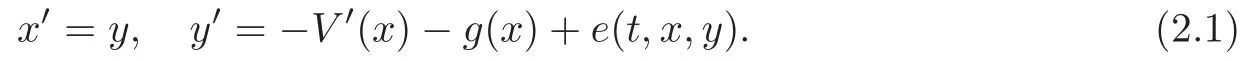
In order to introduce action and angle variables,we consider the auxiliary autonomous system

From our assumptions,we know that all solutions of this system are 2π-periodic int.For everyh>0,we denote byI(h)the area enclosed by the(closed)curve.Let−1<−αh<0<βhbe such thatV(−αh)=V(βh)=h.Then by(1.2)it follows that

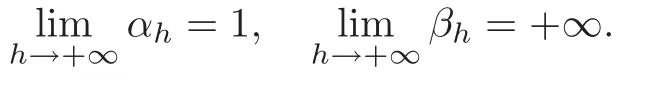
Moreover,it is easy to see that

Let

Then

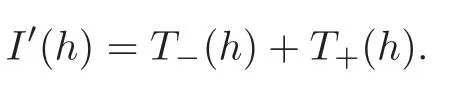
Because all the solutions of the auxiliary equation(2.2)are 2π-periodic,we have

which yields thatI(h)=2πh.

For every(x,y)∈(−1,+∞)×R,let us define the angle and action variables(θ,I)by

where

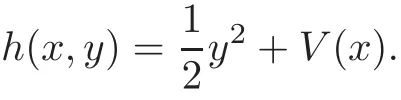
Obviously,we have

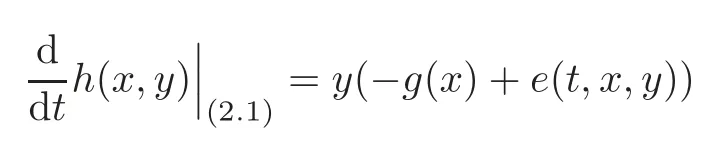
and

In the new variables(θ,I),(2.1)becomes

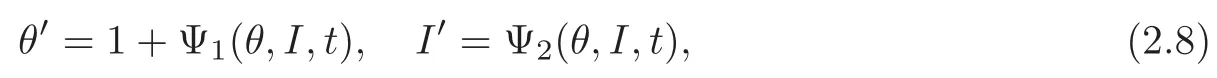
where

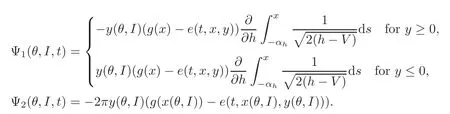
We have used the equality

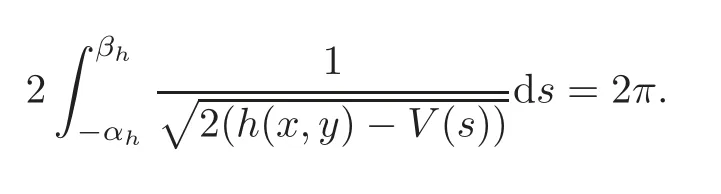
Obviously,this equation is time-reversible with respect to the involution(θ,I)(−θ,I).

3 Some Technical Lemmas

The proof of the main theorem 1.1 is based on a variant of the small twist theorem in the reversible system(see[16]).Therefore,we state it first and then give some technical estimates which will be used in the next sections.More precisely,we may use these estimates to obtain an asymptotic expression of the Poincaré map of(2.8).

3.1 A variant of the small twist theorem

In this subsection,we will state a variant of the small twist theorem(see[16]).

LetA=S1×[a,b]be a finite cylinder with a universal cover A=R×[a,b].The coordinate in A is denoted by(τ,v).Consider a map

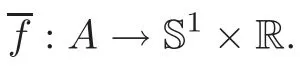
We assume that the map is reversible with respect to the involutionG:(θ,I)(−θ,I),that is,

Suppose thatf:A→R×R,(τ0,v0)(τ1,v1)is a lift ofand it has the form

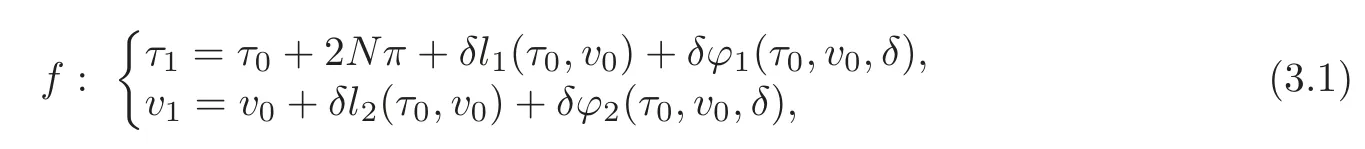
whereNis an integer,δ∈(0,1)is a parameter andl1,l2,ϕ1andϕ2are functions satisfying

In addition,we assume that there exists a functionI:A→R satisfying

Define the functions

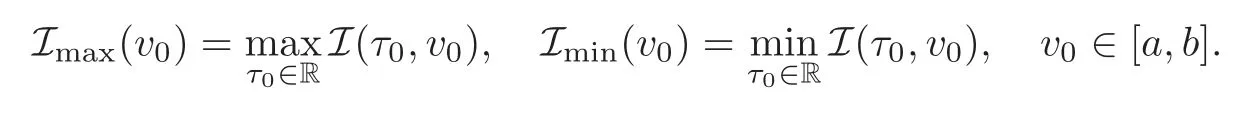
Small Twist Theorem(see[16,Theorem 2])Let be such that(3.1)–(3.3)hold.Assume in addition that there exists a function I satisfying(3.4)–(3.5)and numbers,with

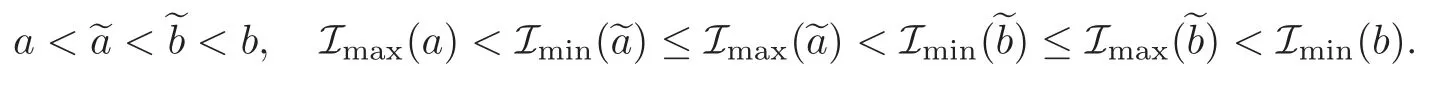
Then there exist >0andΔ>0such that if<Δand,the map has an invariant curveΓ.The constantis independent of .Furthermore,if we denote by μ(Γ,δ)∈S1the rotation number of,then

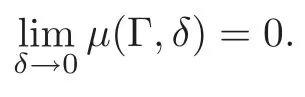
Remark 3.1From the last inequality in(3.2),we know thatτ1is increasing asv0increases.This means that(3.1)is a twist map.By the proof in[16],one can see that the conclusions of this theorem still hold if the condition(3.2)is replaced by

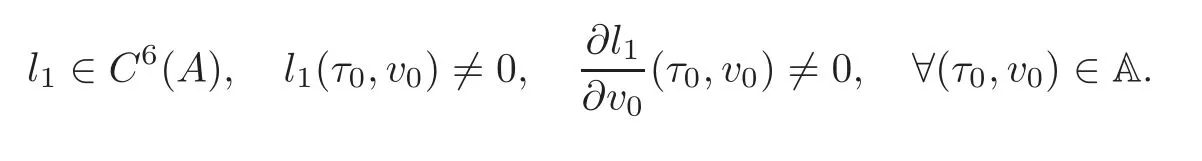
Remark 3.2Note thatl1(τ0,v0)=l1(−τ0,v0),andl2(τ0,v0)=−l2(−τ0,v0).If the functionIdoes not satisfyI(−τ0,v0)=I(τ0,v0),we can chooseJ(τ0,v0)=(I(τ0,v0)+I(−τ0,v0))instead ofI(τ0,v0).

3.2 Some technical lemmas

In order to obtain an asymptotic expression of the Poincaré map of(2.8),we must give some estimates first.In this subsection,we will deal with some technical estimates.Throughout this subsection,we suppose that the assumptions(1)–(5)stated in Section 1 hold.

Lemma 3.1For every positive integer0≤k≤6,there is a constant c1>0,such that

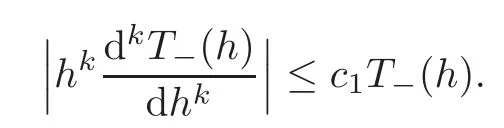
ProofAccording to[13],we know that

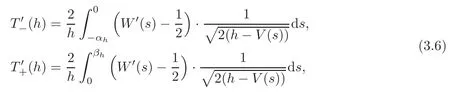
and here and in the rest of this subsection,the functionWis defined by(1.6).By the assumption(2)in Section 1,it follows that

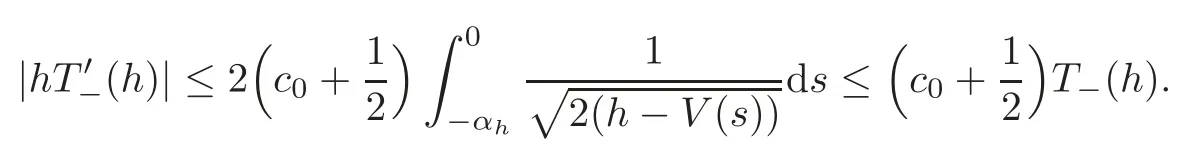
From(3.6)and the equality(the proof can be found in[13])

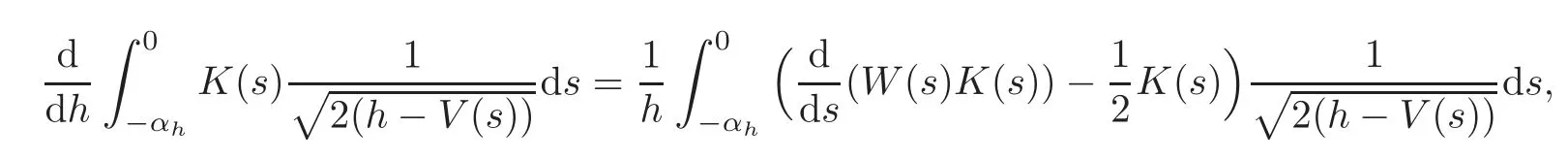
whereKis a smooth function,it follows that

which yields,by the assumption(2)in Section 1 and the estimate on,that

The general case can be obtained by an induction argument and a direct computation.

Lemma 3.2There is a constant c2>0such that,for each positive integer k≤6,

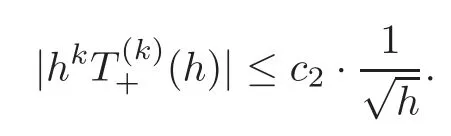
ProofLet

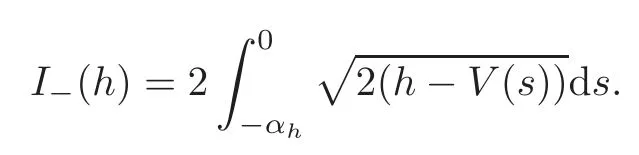
ThenT−(h)=(h).On the other hand,similar to the proof of(3.6),it is not difficult to see that

From the assumption(2)in Section 1,it follows thatBy Lemma 3.1,we have,for each positive integerk≤6,

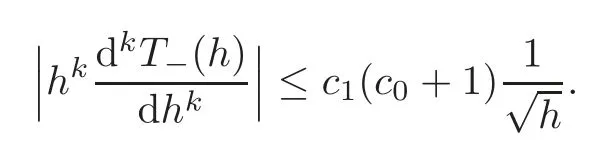
The conclusion of this lemma follows from this inequality and the identityT−(h)+T+(h)≡2π.

Define a functionF

and an operatorL

wheref=f(x,I),h=h(I)andis the derivative ofhwith respect toI.

The proof of the following lemma can be found in[13].

Lemma 3.3For every smooth function g(x,I),we have

Next,we give an estimate of the derivatives ofx=x(θ,I)andy=y(θ,I)with respect to the action variableI.

Proposition 3.1There is a constant C>0such that,for≫1≤k≤6,

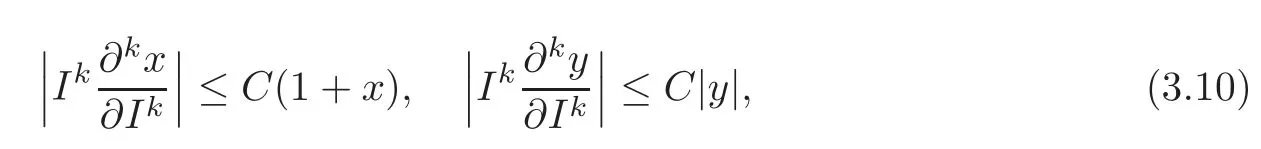
where x=x(θ,I)and y=y(θ,I)are defined implicitly by(2.6)and(2.7),respectively.

The idea of the proof of this proposition is similar to the corresponding one in[13].A complete proof can be found in the appendix of[15].

Note that−1≤−αh≤x≤βhand the assumption(5)in Section 1,there is a constantc3>0 such that for≫I1,.Hence,by Proposition 3.1,we have

wherec4>0 is a constant,not depending onI.

4 An Asymptotic Formula of x(θ,I)

In this section,we will give an asymptotic expression ofx(θ,I)whenI≫1.

From the Definition ofθ(cf.(2.6)),it follows that

xθ(θ,I)=y(θ,I).

Sincecombining with the above equality,we have

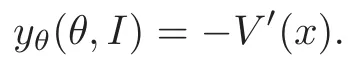
That is,the functionx(θ,I)satisfies

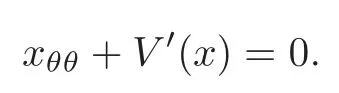
Let

Then

Obviously,there is aδ>0 such that(θ)>0 forθ∈(0,δ).By the assumption(5)in Section 1,we know that,if>0,then it is the solution of

Let+(I)be the subset of the interval[0,2π]such that forθ∈+(I),(θ,I)>0.

Lemma 4.1For θ∈+(I),the functionx has the following expression:

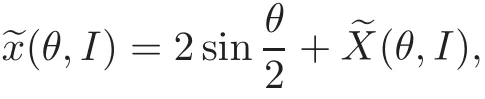
where the functionsatisfies

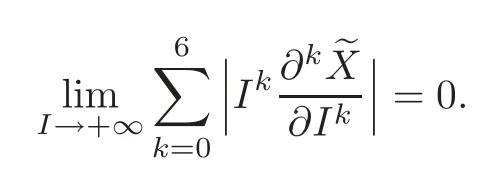
ProofIn the following,we assume thatθ∈+(I).Sinceis the solution of(4.1)with the initial conditionu(0)=0,(0)=1,we have

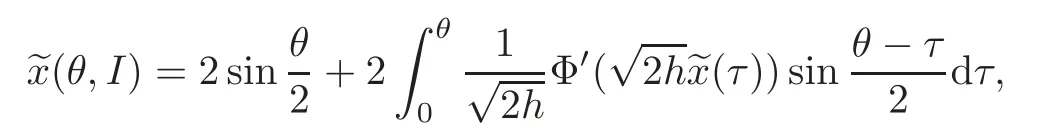
whereHence,the functionis determined implicitly by

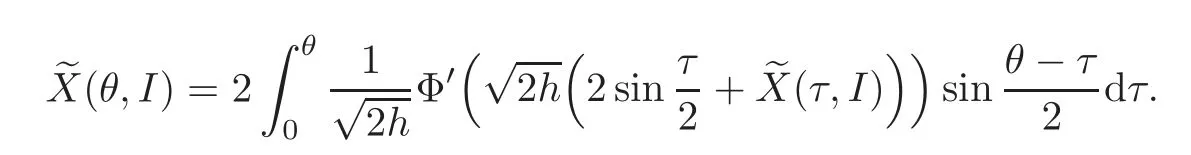
From the hypothesis(5)in Section 1 and the Lebesgue dominated theorem,we have

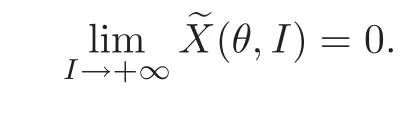
Taking the derivative with respect toIin both sides of the above equality,one has

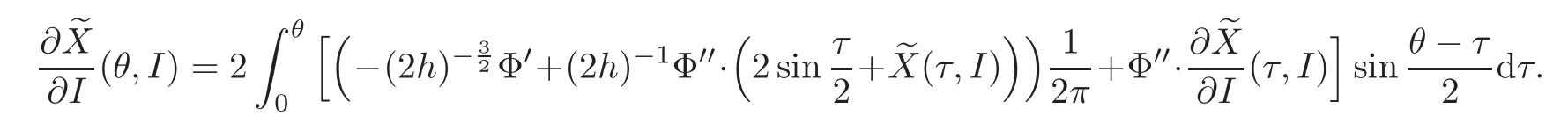
By the hypothesis(5)in Section 1 and the Gronwall inequality,it follows that

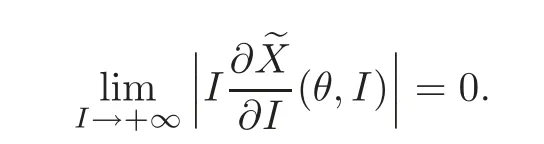
The estimates for the derivatives of higher order can be obtained in a similar way.

By the Definition ofandwe have

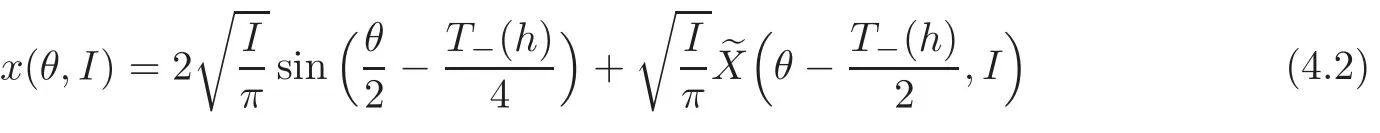
and

Now we turn to estimate the measure of the setBy the Definitions ofθand,we

know that

Hence,Because(1.3)is isochronous,we have,by Lemma 3.2,that

T+(h)=2π−T−(h).

So

whereμdenotes the Lebesgue measure.

Let

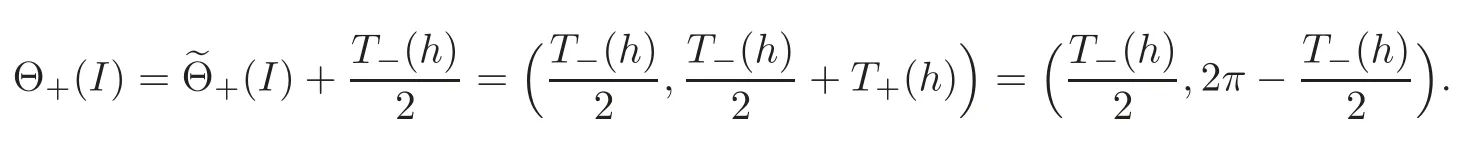
Then

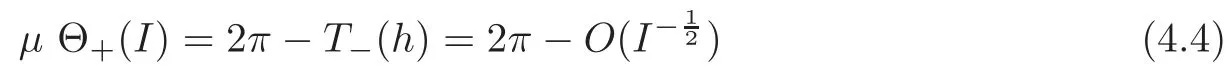
andθ∈Θ+(I)⇐⇒x(θ,I)>0.

In the next section,we introduce a canonical transformation such that the transformed system is a perturbation of an integrable system.

5 Another Set of Action and Angle Variables

Now we consider the system(2.8).Note that

We have,by Lemma 3.3,

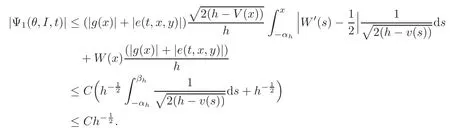
Hence,from(2.8),we know that

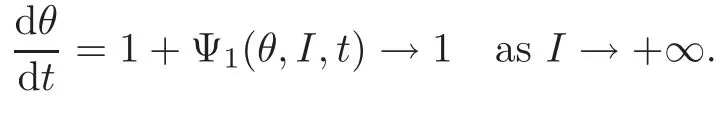
Instead of(2.8),we will consider the following system:

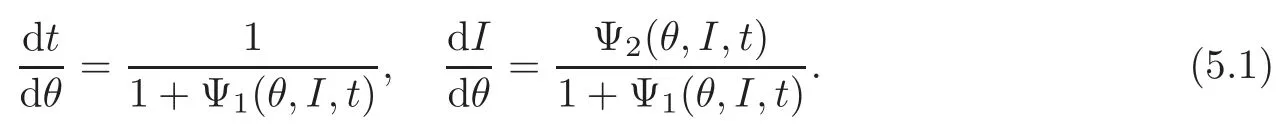
The relation between(2.8)and(5.1)is that if(I(t),θ(t))is a solution of(2.8)and the inverse functiont(θ)ofθ(t)exists,then(I(t(θ)),t(θ))is a solution of(5.1)and vice versa.Hence in order to find quasi-periodic solutions of(2.8)and to obtain the boundedness of the solutions,it is sufficient to prove the existence of quasi-periodic solutions and the boundedness of solutions of(5.1).This trick was used in[13]in the proof of boundedness for superquadratic potentials.

From the Definition ofθ,we have,fory>0,

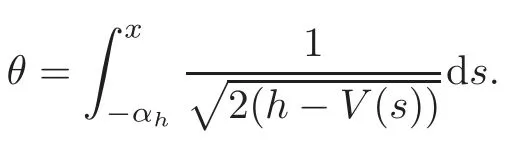
SinceI=2πh,take the derivative with respect to the action variableIin both sides of the above equality(the angle variableθis independent ofI),it follows that

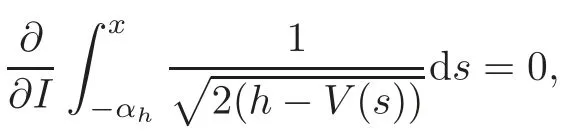
which yields that

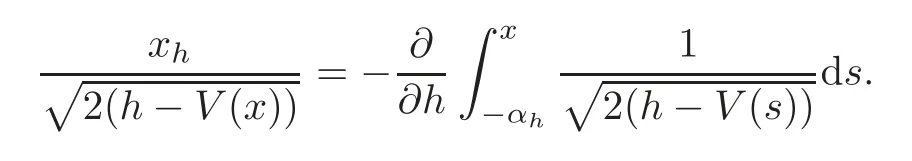
Hence,we obtain that

Ψ1(θ,I,t)=2πxI(g(x(θ,I))−e(t,x(θ,I),y(θ,I))).

Definition 5.1We say a function g(t,ρ,θ,)∈Ok(1)if g is smooth in(t,ρ)and for k1+k2≤k,

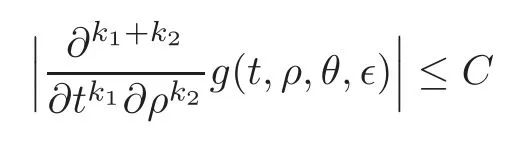
for some constant C>0which is independent of the arguments t,ρ,θ and.Similarly,we say a function g(t,ρ,θ,)∈ok(1)if g is smooth in(t,ρ)and for k1+k2≤k,

Now we introduce a new action variableρ∈[1,2]and a parameter>0 byI=−2ρ.Then,I≫1⇐⇒0<≪1.Under this transformation,the system(5.1)is changed into the form

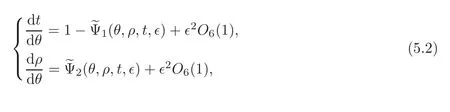
where

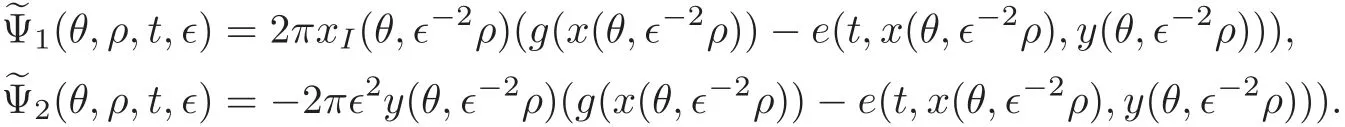
Obviously,if≪1,the solution(t(θ,t0,ρ0),ρ(θ,t0,ρ0))of(5.2)with the initial data(t0,ρ0)∈R×[1,2]is defined in the intervalθ∈[0,2π]andρ(θ,t0,ρ0)∈[,3].So the Poincarmap of(5.2)is well defined in the domain R×[1,2].

Lemma 5.1The Poincaré map of(5.2)is reversible with respect to the involution(t,ρ)(−t,ρ).

By(4.4)and Lemma 3.1,we know that,there is a functionηsuch that

whereη∈O6(1).By the Definition of Θ+and Θ−,we have

6 Proof of the Main Result

In this section, firstly,using the estimates in Subsection 3.2,we will obtain an asymptotic expression of the Poincaré map of(5.2)as≪1.After that,we can prove the main result using a variant of Moser’s small twist theorem in[16].

We make the ansatz that the solution of(5.2)with the initial condition(t(0),ρ(0))=(t0,ρ0) is of the form

t=t0+θ+Σ1(t0,ρ0,θ;),ρ=ρ0+Σ2(t0,ρ0,θ;).

Then,the Poincaré map of(5.2)is

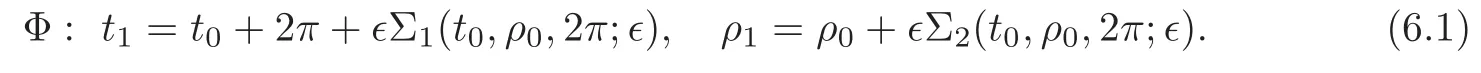
The functions Σ1and Σ2satisfy

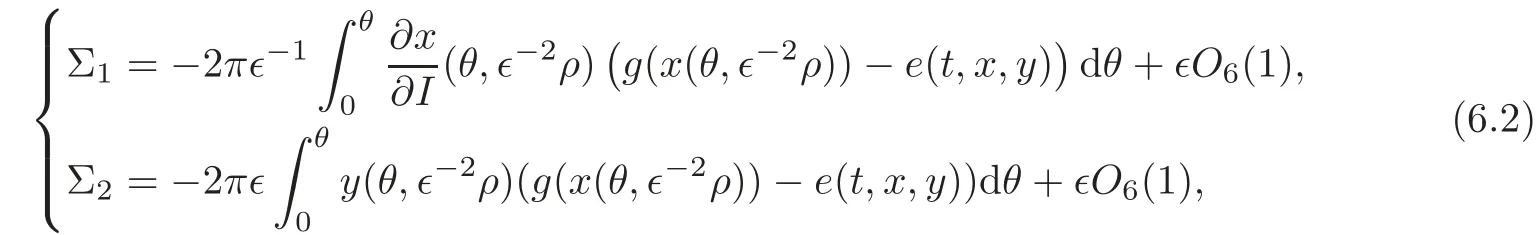
where

By Proposition 3.1 and the assumptions(1)–(5)in Section 1,we know that the terms in the right-hand side of the above equations are bounded,so we have

wherec8>0 is a constant.Hence,forρ0∈[1,2],we may choosesufficiently small such that

for(t0,θ)∈[0,2π]×[0,2π].Similar to the proof in[6],one can obtain

Lemma 6.1The following estimates hold:

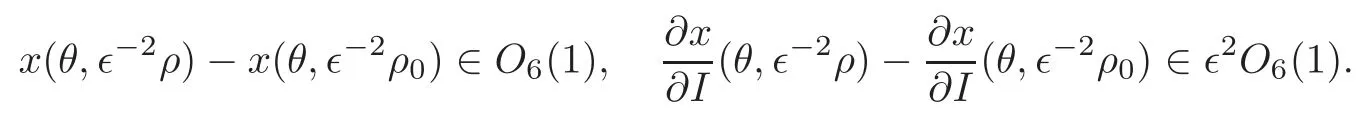
ProofLet

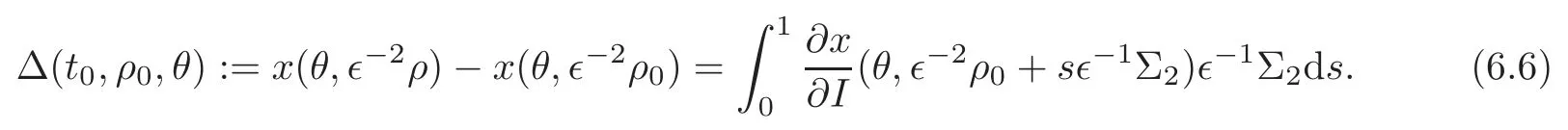
By(3.11)and(6.4),we have

Taking the derivative with respect toρ0in the both sides of(6.6),we have

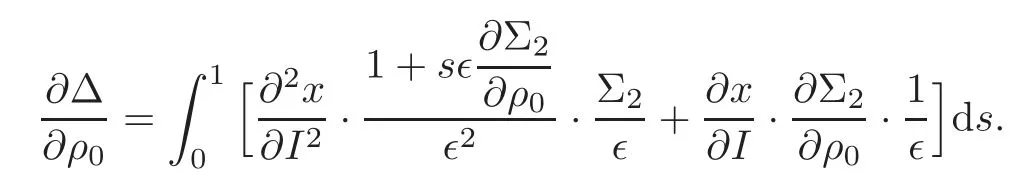
Using(3.11)and(6.5),one may find a constantc9>0 such that

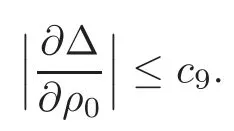
Analogously,one may obtain,by a direct but cumbersome computation,that

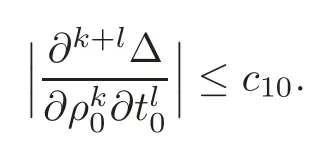
The estimates forfollow from a similar argument,and we omit it here.

Now we turn to give an asymptotic expression of the Poincaré map of(5.2),that is,we study the behavior of the functions Σ1and Σ2atθ=2πas0.

By(6.2)and Lemma 6.1,it follows that

and

withx=x(θ,−2ρ0),y=y(θ,−2ρ0).Here we have used thaty(−θ,−2ρ0)=−y(θ,−2ρ0)andx(−θ,−2ρ0)=x(θ,−2ρ0).By Proposition 3.1,we know that whenθ∈Θ−(I),

which yield that

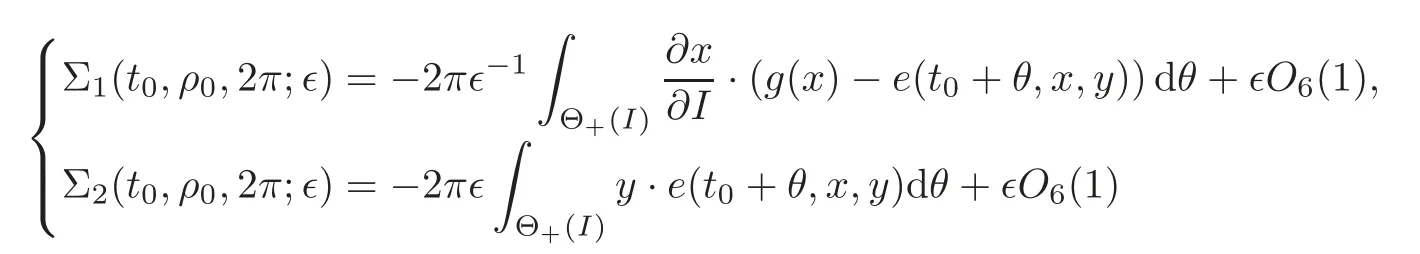
withx=x(θ,−2ρ0),y=y(θ,−2ρ0).

Our next task is to estimate the above two integrals.

Lemma 6.2Ifand the assumption(4)in Section1holds,then,forany function f∈o6(1),

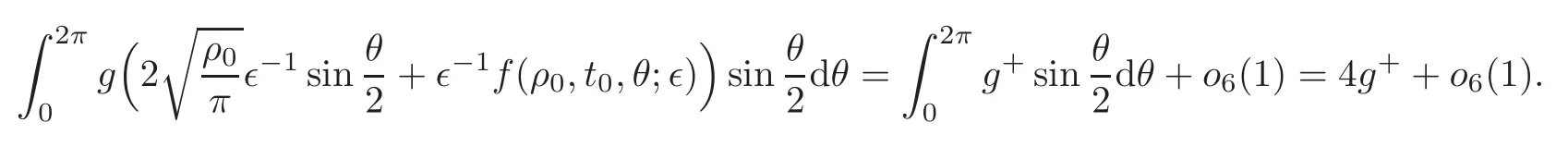
ProofLet

Note that sin>0 forθ∈(0,2π),so by the Lebesgue dominated theorem,we have

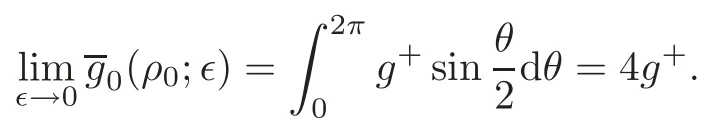
Since

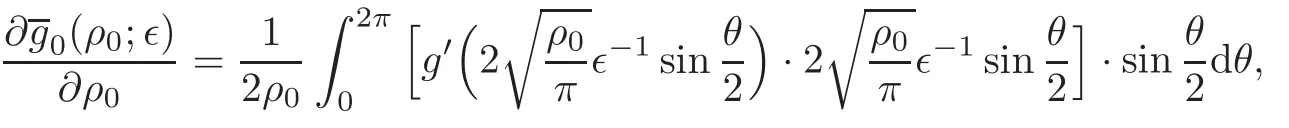
by the assumption(4)in Section 1 and the Lebesgue dominated theorem,it follows that

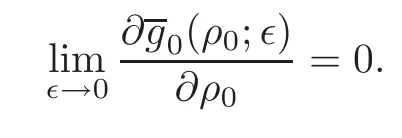
The estimates for the derivatives of higher order can be obtained in a similar way.Hence,we have proved the conclusion whenf≡0.In the general case,let

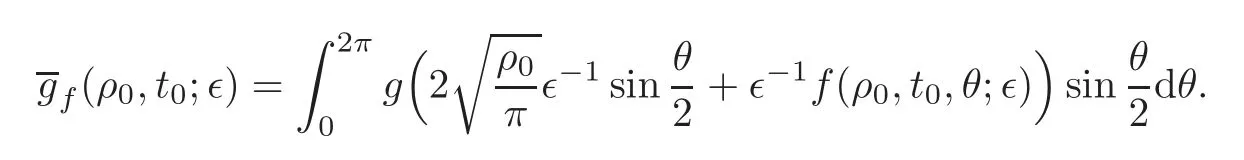
Then

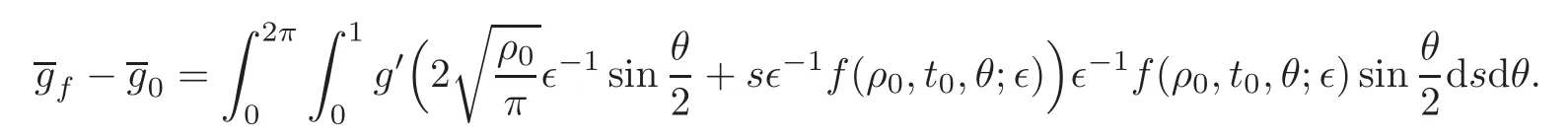
The conclusion follows from the Lebesgue dominated theorem and the assumption(4)in Section 1.

Lemma 6.3If the assumption(6)holds,then,for any function f1,f2∈o6(1),

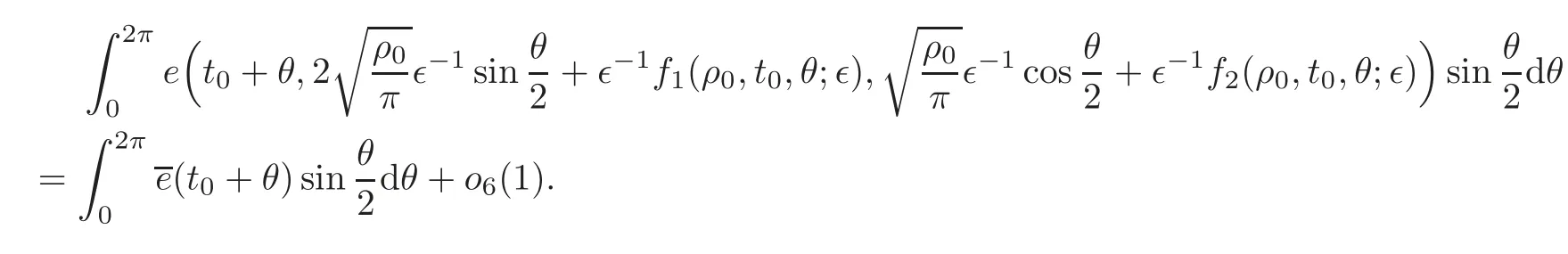
ProofLet

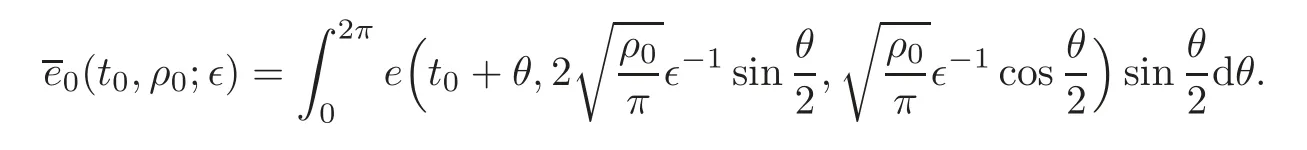
Note that sin>0 forθ∈(0,2π),so by Lebesgue dominated theorem,we have

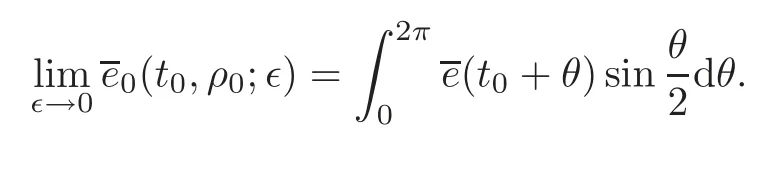
Since

by the assumption(6)in Section 1 and the Lebesgue dominated theorem,it follows that

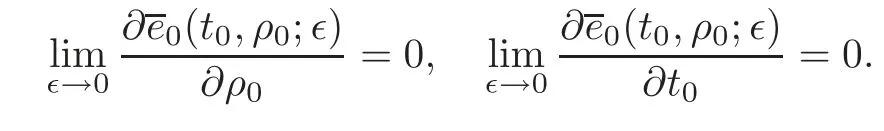
The estimates for the derivatives of higher order can be obtained in a similar way.Hence,we have proved the conclusion whenf1=f2≡0.In the general case,let

Then

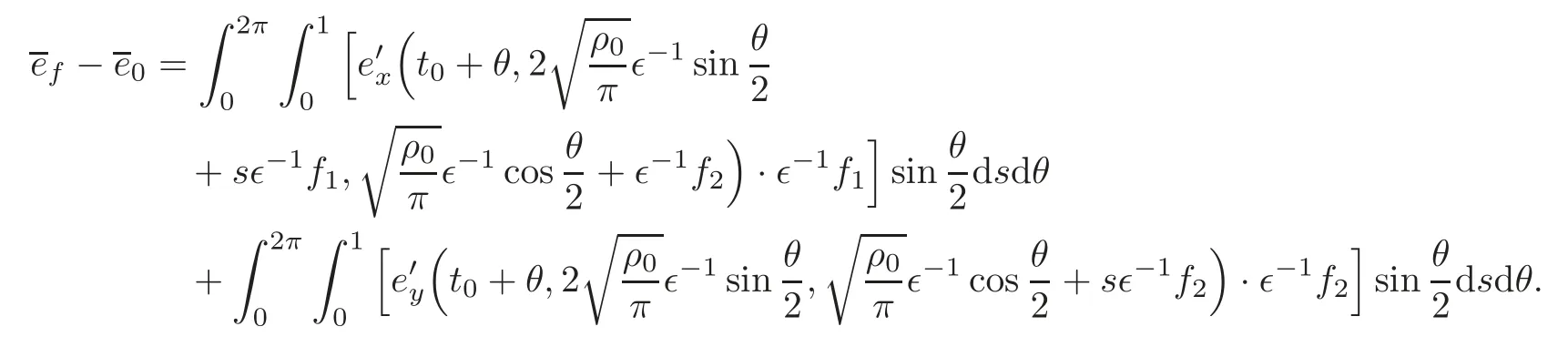
The conclusion follows from the Lebesgue dominated theorem and the assumption(6)in Section 1.

Similarly,we have the following Lemma.

Lemma 6.4If the assumption(6)in Section1holds,then

From these lemmas,we have the following lemma.

Lemma 6.5The following estimates hold:

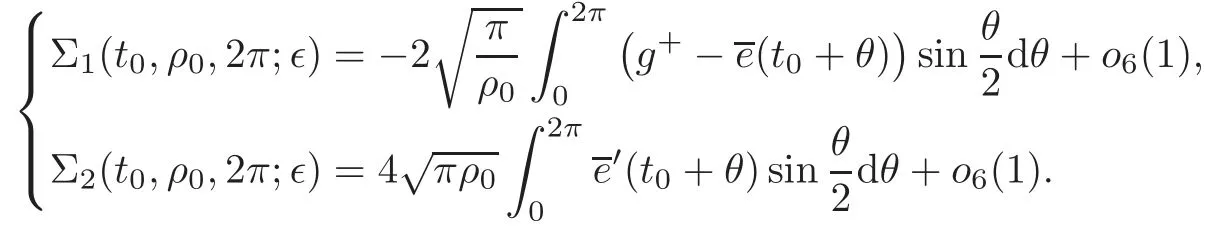
ProofBy(4.2)–(4.3),the Definition of Θ+and(5.3),it follows that

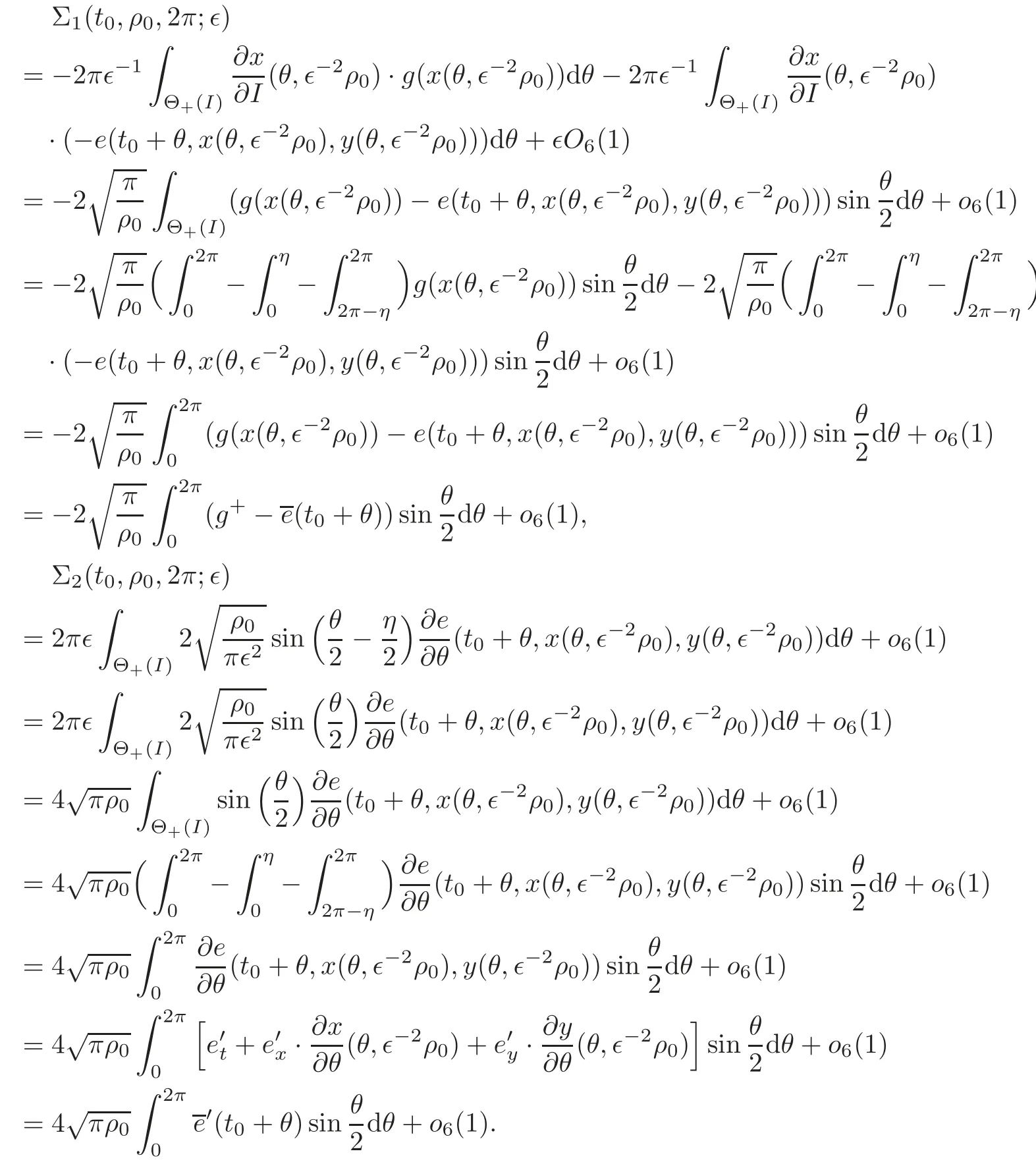
Let

Then there are two functionsφ1andφ2,such that the Poincaré map of(5.2),given by(6.1),is of the form

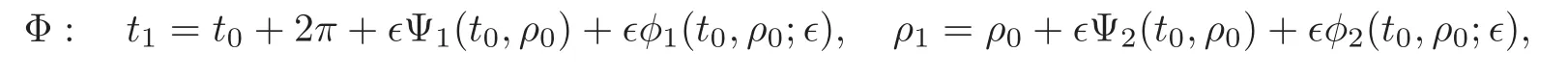
whereφ1,φ2∈o6(1).

Note that,by the Lazer-Landesman condition 4g+>maxθ∗(θ),we know that

Let

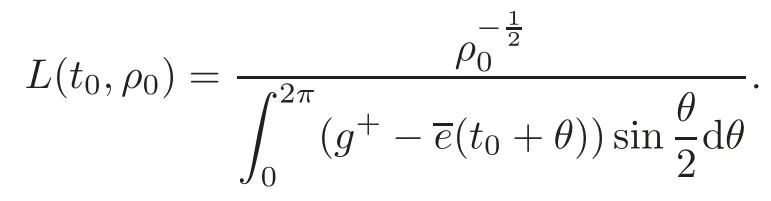
Then

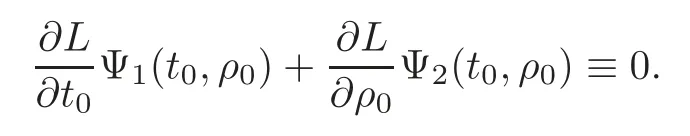
The other assumptions of Ortega’s theorem are veri fied directly.Hence,for sufficiently small,there is an invariant curve of Φ in the annulus(t0,ρ0)∈S1×[1,2].The boundedness of the solutions to our original equation(1.5)can be obtained by the existence of such invariant curves,and the precise proof can be found in[14].

Moreover,the solutions starting from such curves are quasi-periodic solutions.Using the Poincaré-Birkho ff fixed point theorem,there is a positive integern0,such that,for anyn≥n0,there are at least two periodic solutions of(1.5)with the minimal period 2nπ(see[6]).

Since then,we are done with the proof of the existence of the quasi-periodic solutions and boundedness of all solutions for reversible forced isochronous oscillators with a repulsive singularity.

[1]Bonheure,D.,Fabry,C.and Smets,D.,Periodic solutions of forced isochronous oscillators at resonance,Discrete and Continuous Dynamical Systems,8,2002,907–930.

[2]Capietto,A.,Dambrosio,W.and Liu,B.,On the boundedness of solutions to a nonlinear singular oscillator,Z.angew.Math.Phys.60,2009,1007–1034.

[3]Chavarriga,J.and Sabatini,M.,A survey of isochronous centers,Qualitative Theory of Dynamical Systems1,1999,1–70.

[4]Del Pino,M.and Man´asevich,R.,In finitely many 2π-periodic solutions for a problem arising in nonlinear elasticity,J.Differential Equations,103,1993,260–277.

[5]Del Pino,M.,Man´asevich,R.and Montero,A.,T-periodic solutions for some second order differential equations with singularities,Proc.Roy.Soc.Edinburgh Sect.A,120,1992,231–243.

[6]Dieckerho ff,R.and Zehnder,E.,Boundedness of solutions via the twist theorem,Ann.Scula.Norm.Sup.Pisa Cl.Sci.,14(1),1987,79–95.

[7]Fabry,C.,Landesman-Lazer conditions for periodic boundary value problems with asymmetric nonlinearities,J.Differential Equations,116,1995,405–418.

[8]Fabry,C.,Behavior of forced asymmetric oscillators at resonance,Electron.J.Differential Equations,2000,2000,1–15.

[9]Fabry,C.and Fonda,A.,Nonlinear resonance in asymmetric oscillators,J.Differential Equations,147,1998,58–78.

[10]Fabry,C.and Man´asevich,R.,Equations with ap-Laplacian and an asymmetric nonlinear term,Discrete Continuous Dynamical Systems,7,2001,545–557.

[11]Fabry,C.and Mawhin,J.,Oscillations of a forced asymmetric oscillator at resonance,Nonlinearity,13,2000,493–505.

[12]Lazer,A.C.and Leach,D.E.,Bounded perturbations of forced harmonic oscillators at resonance,Ann.Mat.Pura Appl.,82,1969,49–68.

[13]Levi,M.,Quasiperiodic motions in superquadratic time-periodic potentials,Commun.Math.Phys.,143,1991,43–83.

[14]Liu,B.,Boundedness in nonlinear oscillations at resonance,J.Differential Equations,153,1999,142–174.[15]Liu,B.,Quasi-periodic solutions of forced isochronous oscillators at resonance,J.Differential Equations,246,2009,3471–3495.

[16]Liu,B.and Song,J.,Invariant curves of reversible mappings with small twist,Acta Math.Sin.,20,2004,15–24.

[17]Ortega,R.,Asymmetric oscillators and twist mappings,J.London Math.Soc.,53,1996,325–342.

[18]Ortega,R.,Boundedness in a piecewise linear oscillator and a variant of the small twist theorem,Proc.London Math.Soc.,79,1999,381–413.

[19]Ortega,R.,Twist mappings,invariant curves and periodic differential equations,Progress in Nonlinear Differential Equations and Their Applications,43,Grossinho M.R.et al,eds,Birkh¨auser,2001,85–112.