Ga-F共掺杂ZnO导电性和透射率的第一性原理计算

何静芳 吴 一 史茹倩 周鹏力 郑树凯＊,

(1河北大学电子信息工程学院计算材料与器件模拟研究中心，保定071002)

(2西安电子科技大学通信工程学院，西安710071)

Ga-F共掺杂ZnO导电性和透射率的第一性原理计算

何静芳1,2吴 一1史茹倩1周鹏力1,2郑树凯＊,1

(1河北大学电子信息工程学院计算材料与器件模拟研究中心，保定071002)

(2西安电子科技大学通信工程学院，西安710071)

采用基于密度泛函理论的第一性原理平面波超软赝势方法，对本征ZnO，Ga、F单掺ZnO和Ga-F共掺ZnO的几何结构进行优化后计算了各体系的相关性质。结果表明各掺杂体系有各自的优缺点，在制作透明导电薄膜时可根据具体要求采取不同的掺杂方案。Ga掺杂ZnO比F掺杂ZnO的晶格畸变小。相同环境下Ga原子比F原子更容易进入ZnO晶格，因此掺杂后结构更加稳定。Ga、F掺杂都改善了ZnO的导电性，掺杂ZnO的载流子浓度比本征ZnO增加了3个数量级，相同浓度的F掺杂比Ga掺杂能产生更多的载流子。Ga-F共掺杂ZnO折中了上述Ga、F单掺杂ZnO的优缺点。另外，掺杂后ZnO的吸收边蓝移，以Ga-F共掺杂ZnO在紫外区域的透射率最大，在280～380 nm范围内其透射率在90%以上。

ZnO；第一性原理；载流子浓度；光学性质；透射率

0 引言

透明导电氧化物(TCO)薄膜具有禁带宽、可见光谱区光透射率高和电阻率低等光电特性，广泛地应用于太阳能电池、平面显示、特殊功能窗口涂层及其它光电器件领域。传统的TCO材料为掺锡氧化铟(ITO)，但是铟为稀散元素，价格较高，而且ITO应用于太阳能电池时在等离子体中不够稳定[1]。相比之下，六方纤锌矿型ZnO基薄膜由于其原料易得、制造成本低廉、无毒、易于实现掺杂，且在等离子体中稳定性好等优点，有可能成为ITO的替代产品。在制作工艺上，为了满足高透明度和低电阻率的需求，人们对TCO薄膜的研究除了制备方法外，还包括对制备好的TCO膜进行后续处理(如表面微纳米结构复合、热退火、激光退火)[2]。

对于ZnO薄膜的掺杂改性，三价阳离子Ga3+(0.062 nm)由于半径与Zn2+离子(0.074 nm)相近而得到了广泛研究。Estrich等[3]用脉冲激光沉积的方法制备了Ga掺杂ZnO(GZO)薄膜，发现当Ga掺杂量是1mol%时，薄膜透射率为90%，电阻率大约为1× 10-3Ω·cm。并且指出将TCO作为抗反射涂层(ARC)，可获得不需ARC的太阳电池发射极。Li等[4]用射频磁控溅射法在聚碳酸酯衬底上制备了GZO薄膜，研究了溅射压力和氧分压对薄膜质量的影响，结果表明电阻率对氧分压的变化非常敏感，氧分压每增加4.8%，电阻率增加106倍，并且随溅射压力的减小而减小，当溅射压为0.14 Pa时，电阻率仅为7.8×10-4Ω·cm。Jing等[5]用水热法合成了GZO纳米片，X射线光谱显示Ga存在于ZnO薄膜中，并且进入ZnO晶格，在Ga掺杂浓度为2%时，获得最低电阻率为2.3×10-4Ω·cm。同样，阴离子F-(0.131 nm)由于与O2-(0.138 nm)半径相近也备受关注。Cao等[6]用脉冲激光电极法在石英衬底上制备F掺杂ZnO (FZO)透明导电薄膜，研究了衬底温度对ZnO薄膜的结构及光电性质的影响。发现在300℃时，薄膜有最低的电阻率5.15×10-4Ω·cm，对应载流子浓度5.27×1020cm-3，在可见光范围内平均光学透射率高于90%。Nam等[7]用简易非醇盐凝胶旋镀法在玻璃衬底上淀积FZO薄膜，发现F含量对薄膜的结构、电阻率、载流子浓度、迁移率和光学透射率都有非常大的影响。当F含量大于5at%时，这些性质会退化。Choi等[8]发现阴阳离子以低浓度共掺入ZnO薄膜中可以优化其导电性。为此，Qian等[9]用中频磁控溅射法首次在聚碳酸酯衬底上制备了Ga-F共掺杂ZnO (GFZO)薄膜，并与Al掺杂ZnO薄膜(AZO)进行了详细对比，研究了掺杂对ZnO薄膜的结构和光电性质的影响。发现GFZO薄膜与AZO薄膜相比有更好的结晶度。AZO的电阻率为2.3×10-2Ω·cm，透射率为75%，而GFZO薄膜有更低的电阻率(1.4×10-3Ω·cm)和更高的透射率(81%)。表明Ga-F共掺杂的协同效应会使晶格损伤密度减小，可以优化ZnO基薄膜的光电性质。

虽然实验上对比了Ga-F共掺杂ZnO与Al掺杂ZnO的性质，但目前还未见在相同条件下对比Ga、F单掺杂ZnO与Ga-F共掺杂ZnO性质的报道。尤其对材料透射率的第一性原理计算在之前的文献中也未曾看到过。本文通过第一性原理计算Ga、F单掺杂与Ga-F共掺杂ZnO的晶胞参数和态密度等来研究Ga-F共掺是否会带来协同效应，并计算了各体系的载流子浓度和光学透射率，由此对比各种掺杂方案的优缺点。

1 构建模型

1.1 理论模型

理想ZnO是六方纤锌矿结构，所属空间群为P63mc，其晶胞由O原子的六角密堆积和Zn原子的六角密堆积在c轴方向反向嵌套而成。晶格常数实验值a=b=0.324 9 nm，c=0.520 6 nm，α=β=90°，γ= 120°。本文选取3×3×2的ZnO超晶胞为本征ZnO模型，在此基础上，以不同数量的F原子替代O原子，不同数量的Ga原子替代Zn原子，构建了不同浓度的掺杂ZnO体系。若以N个掺杂原子替换超晶胞中的N个原子，则该原子的浓度c=N/72×100%。取N= 1，构建了掺杂浓度为1.39at%的F单掺杂ZnO体系(F-ZnO)和Ga单掺杂ZnO体系(Ga-ZnO)。取N=2，构建了掺杂浓度为2.78at%的F单掺杂ZnO体系(2FZnO)和Ga单掺杂ZnO体系(2Ga-ZnO)。另外还构建了Ga、F含量均为1.39at%的Ga、F共掺杂ZnO体系(Ga，F-ZnO)。其中，Ga，F-ZnO体系模型如图1所示。

1.2 计算方法

文中所有的计算工作均由CASTEP软件包完成。CASTEP软件是一个基于密度泛函理论的计算材料学程序：在晶体周期性势场中，采用周期性边界条件，将多电子体系波函数用平面波基组展开。为了尽量减少平面波基矢，采用超软赝势来描述离子实与价电子之间的相互作用势，电子-电子相互作用的交换关联势由广义梯度近似校正，并采用Perdew、Burke和Ernzerhof所提出的关联梯度修正泛函。利用数值化的原子轨道作基矢，基函数采用双指极基组，迭代过程中收敛精度为每原子1×10-5eV，原子间相互作用力的收敛精度为0.3 eV·nm-1，晶体内应力收敛精度为0.05 GPa，原子的最大位移收敛精度为0.001 nm，平面波截断能量为340 eV。系统在优化结构和计算总能量时布里渊区的k空间网格点均为3×3×2。选取Zn、O、Ga、F的价电子组态分别为Zn3d104s2，O2s22p3，Ga3d104s24p1，F2s22p5。

2 结果与讨论

2.1 晶体结构

几何优化后的超晶胞参数与各类原子成键的平均键长见表1。在F掺杂ZnO中，Zn-O键的键长基本不变。由于F掺入ZnO后以-1价存在，F-离子与Zn2+离子的库仑吸引力比O2-离子与Zn2+离子的吸引力小，造成Zn-F键的键长大于Zn-O键的键长，因此与本征ZnO相比，2F-ZnO的晶胞体积变大。由于Ga3+的半径(0.062 nm)小于Zn2+的半径(0.074 nm)，Ga-O键键长小于Zn-O键键长，Ga掺杂后ZnO的晶胞体积会变小。但是由于Ga3+替换Zn2+后吸引周围的O2-离子，排斥周围的Zn2+离子，使Ga周围的Zn-O键键长(0.208 2 nm)增加，晶胞体积会增大。在上述两种因素共同作用下，2Ga-ZnO的晶胞体积略有增加。Ga，F-ZnO的晶胞畸变比2Ga-ZnO大，比2FZnO小。

2.2 掺杂稳定性

缺陷或杂质X在电荷态为q时的形成能可表示为[10]

式(1)中，Etot[Xq]为缺陷或杂质X在电荷态为q时体系的总能量，Etot[ZnO,bulk]为本征ZnO体材料的总能量，ni为体系中原子被移除(ni＜0)或被引入(ni＞0)的个数。μi为元素i在特定环境下的化学势，μi=Δμi+ μi0，其中μi0由元素i所构成的块材或气体分子的总能量决定，Δμi为元素i在特定环境下的相对化学势。EF为相对于价带顶的费米能级，Ev为本征ZnO的价带顶，“位势矫正”项ΔV为含杂质的超晶胞与不含杂质的超晶胞间的静电势之差。

为了得到各个元素的化学势，要构建相应的单质。μZn0=1/2EZn，μGa0=1/4EGa，μO0=1/2EO，μF0=1/2EF2，其中，EZn和EGa分别为Zn和Ga原胞的总能量，EO2和EF2分别为氧分子和氟分子放置在1.5×1.5×1.5 nm3立方体中的总能量。元素的化学势还和其生长环境密切相关。ZnO可以在富氧环境中生长，也可以在富锌环境中生长。在富锌条件下，ΔμZn=0，在富氧条件下，ΔμO=0。要形成ZnO，必须满足其中ZnO的形成焓为 ZnO原胞总能量，计算得到=-3.51 eV，与实验值-3.56 eV基本吻合[11]。本文还考虑了可能出现的竞争相化合物Ga2O3和ZnF2，Ga2O3的形成焓=-10.99 eV，ZnF2的形成焓为了不出现竞争相化合物，需有成立。由于竞争相的出现，在不同相时，ΔμGa与ΔμO及ΔμF与ΔμZn满足不同的关系。

表1 优化后的超晶胞参数与键长Table1 Optimized supercell parameters and bond lengths

ΔμGa随ΔμO的变化曲线如图2(a)所示，图中折线的表达式为：

从图中得出，当ΔμO小于-3.66 eV时，Ga为金属相；ΔμO在-3.66 eV处，Ga由金属相向Ga2O3相转变；当ΔμO在-3.66～0 eV范围内，Ga以Ga2O3相存在。

ΔμF随ΔμZn的变化曲线如图2(b)所示，图中折线的表达式为：

当ΔμF小于-6.84 eV时，F为气相；ΔμF在-3.66～0 eV范围内，F以ZnF2相存在。

形成能越低意味着掺杂后体系越稳定，掺杂越容易进行。计算得到各掺杂体系在不同生长环境下的中性形成能，如表2所示。可以看出，对于计算的5种掺杂体系，富锌环境比富氧环境下的形成能低，更利于实现掺杂。显而易见，富锌环境下，F原子容易替代O位，Ga原子却不容易替代Zn位，但由于在富氧环境下很容易形成Ga的竞争化合物Ga2O3，因此富锌环境同样有利于Ga的掺入。通过横向对比富锌环境下不同体系的形成能可知，Ga比F更容易进入ZnO晶格，实现稳定的掺杂。这是由于Ga以+3价存在于ZnO中，与+2价的Zn相比，其与O2-离子有更强的库仑吸引力，相反相较于O2-离子，F-离子与Zn2+离子的库仑吸引力却减弱了。随着掺杂浓度的提高，形成能变大，在Ga-ZnO体系中掺入F的形成能(0.616 eV)比在F-ZnO体系中掺入F的形成能(0.701 eV)低，说明掺入Ga有利于减小F替位O的形成能。

图2 氧元素和锌元素的相对化学势Fig.2 Relative chemical potentials of O and Zn elements

表2 各掺杂ZnO体系在不同生长环境下的中性形成能Table2 Neutral formation energy of every doped ZnO in different growth environment eV

2.3 载流子浓度和态密度分析

掺杂前后ZnO的总态密度(TDOS)如图3所示，虚线位置表示费米能级(EF=0 eV)。在四面体配位场作用下Zn3d态从五重简并态被劈裂为能量较低的二重简并e态(dz2，dx2-y2)和能量较高的三重简并t2态(dxy，dyz，dxz)[12]。在-6.85～-0.22 eV范围内为本征ZnO的价带，t2态与O2p态作用构成成键轨道与反键轨道，成键的t2态能量下降，比e态能量还要低[13]，成键轨道的主峰p1位于-5.70 eV处，反键轨道的主峰p3位于-1.53 eV处，e态为非键轨道，对应-4.74 eV处的p2峰。O2p态与Zn4s态作用也构成成键与反键轨道，其中构成导带的反键轨道位于1.00～5.09 eV范围内，呈现较强的离域性。掺入F和Ga后，价带部分形状基本不变，仍有p1、p2、p3三个峰，但峰值均有所减小。

图3 各ZnO体系的总态密度图Fig.3 TDOS of every ZnO system

从图3中可以看出掺杂未在禁带中引入孤立的杂质能级，因此掺杂前后电子均服从费米分布

在室温下T=300 K，k0为玻耳兹曼常数。半导体的载流子浓度为电子和空穴浓度之和，热平衡状态下导带电子浓度n0和价带空穴浓度p0分别为[14]

其中V为超晶胞体积，Ec′、Ec、Ev、Ev′分别为导带顶、导带底、价带顶和价带底能量，gc(E)和gv(E)分别为导带底和价带顶附近状态密度。

计算得到的掺杂前后各ZnO体系的载流子浓度见表3。实验中测定室温下SiO2衬底上生长的ZnO薄膜载流子浓度为2.04×1018cm-3[15]。在Al2O3衬底上生长的ZnO薄膜经不同氧分压下退火后，载流子浓度在1.9×1018到3.6×1018cm-3之间[16]。可见计算得到的本征ZnO载流子浓度的数量级与实验数据相同。掺杂后载流子浓度的数量级在1021，其中，单掺杂体系的载流子浓度与实验数据(数量级在1020，1021)比较符合[17-18]。显然掺杂后载流子浓度提高了3个数量级，ZnO的导电性得到改善。同浓度时，F掺杂比Ga掺杂能产生更多的载流子。掺杂后费米能级进入导带，ZnO变为n型半导体，所以载流子浓度主要和导带底(CBM)到费米能级附近的态密度有关。

图4为各掺杂ZnO体系在CBM～6k0T范围内的分态密度图(PDOS)。掺杂后费米能级处的电子态主要来自Zn4s态、O2p态和O2s态，因此在n型简并的ZnO中导带中的电子更多地占据了Zn、O原子的量子态而非杂质原子的量子态。由于Ga4s的态密度比F2p的态密度大，其与Zn4s态和O2p态的作用更加强烈，从而使Zn4s态和O2p态向高能端和低能端扩展，Ga掺杂ZnO中电子可占据的量子态变少，因此2Ga-ZnO中的载流子浓度小于2F-ZnO的载流子浓度。对比图3中相同原子在不同体系的分态密度可以看到，Ga，F-ZnO中Zn、O的态密度分别为两种单掺杂体系中Zn、O态密度的平均值。而由于共掺杂体系中F、Ga的掺杂量相对于单掺杂体系减半，因此F、Ga的态密度减半。通过上述分析可知Ga-F共掺杂并未对载流子的产生有额外的影响。计算得到Ga，F-ZnO中的载流子浓度为2Ga-ZnO和2F-ZnO中载流子浓度的平均值。

表3 各ZnO体系的载流子浓度Table3 Carrier concentration of every ZnO system

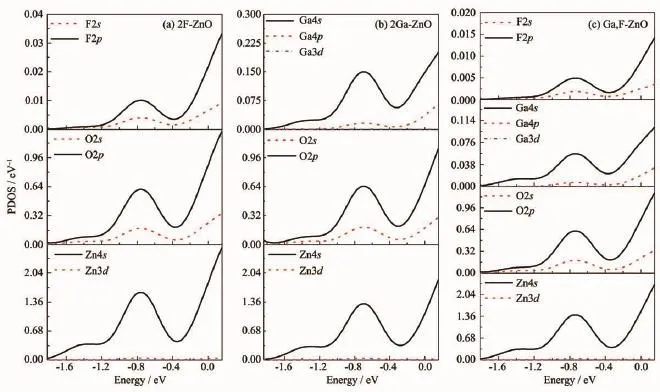
图4 各掺杂ZnO体系的分态密度图Fig.4 PDOS of every doped ZnO system

2.4 光学性质

为研究Ga、F单掺杂与共掺杂ZnO的光学透射性质，首先要计算各体系的吸收系数和反射率，由于ZnO的生长具有c轴择优取向，因此计算时选择垂直入射光的极化方向为(001)方向[11]。同时，用剪刀差算符将带隙修正到实验值，其值为ZnO带隙的实验值(3.37 eV)与计算值(0.717 eV)之差2.653 eV。

吸收系数α表示的是电磁波通过单位厚度的材料时能量的衰减分数。半导体内存在着多种跃迁机制会造成光能的衰减，如带间跃迁、带内跃迁以及与杂质、缺陷、晶格振动有关的跃迁过程。计算得到掺杂前后ZnO的吸收谱如图5(a)所示。从图5(a)可以看出，本征ZnO的吸收谱存在4个明显的峰，分别位于4.78、5.91、8.65和12.1 eV处。掺杂后位于4.78 eV处的峰消失，表明其来源于价带p1峰附近量子态与p3峰附近量子态之间的带内跃迁。其余3个峰在掺杂前后均存在，它们分别来自于价带p2峰附近量子态、p1峰附近量子态与导带底附近的Zn4s态电子之间的带间跃迁和-17.48 eV处O2s态与价带中Zn3d态电子之间的跃迁。在重掺杂情况下吸收边会发生移动。由前面的态密度分析可知，掺杂后半导体发生n型简并，费米能级以下的所有导带态已被电子占据，光吸收的带间跃迁过程只能在价带态和费米能级附近的导带空带之间发生，由此发生伯斯坦莫斯漂移，吸收边向高能方向移动。同时，通过对载流子浓度的计算可知，掺杂后载流子浓度大大增加，带负电的电子会削弱中间离子实的赝势，这种屏蔽效应使半导体禁带宽度趋于收缩，发生能带重整化，吸收边向低能方向移动[19]。由图5(a)可以看出，3种掺杂ZnO体系的吸收边均向低能方向移动，因此能带重整化造成的影响大于伯斯坦莫斯漂移。由于导带内电子增多，n型ZnO导带中带内亚结构之间的跃迁成为可能，单掺杂体系在3.79 eV处出现了一个峰，Ga-F共掺体系在2.76 eV处出现一个峰，其中前者为-1.82 eV处Γ能谷和1.86 eV处的A能谷之间的间接跃迁，后者为-1.82 eV处Γ能谷和0.82 eV处Γ能谷之间的直接跃迁。反射率R表示的是在一个界面反射中，反射波与入射波能量的比值。图5(b)为掺杂前后ZnO的反射谱，反射谱的峰与吸收谱的峰基本对应，掺杂体系的反射率在可见光及紫外光区域有明显的减小。

图5 各ZnO体系的光学吸收谱和反射谱Fig.5 Absorption spectrum and reflectance spectrum of every ZnO system

设光垂直入射到厚度为d的厚膜，忽略干涉效应，透射率T为[20]

文献[6]中制得F掺杂ZnO薄膜的膜厚为300 nm，因此计算时令式(7)中的d=300 nm，计算得到不同掺杂形式下ZnO薄膜的透射光谱如图6所示。从图6可以看出，本征ZnO在可见光区(380～780 nm)的透射率在90%附近，与实验结果相符。掺杂后ZnO吸收边蓝移，因此在紫外光区(200～380 nm)的平均透射率增加。其中在280～380 nm范围内，3种掺杂体系的透射率都在76%以上。Ga-F共掺杂ZnO的透射率最高(＞90%)，2F-ZnO的透射率在85%～90%之间，而2Ga-ZnO体系由于在该区存在峰值较大的吸收峰而出现一个低谷。另外，掺杂后ZnO在500～780 nm的可见光区透过率也有所增长。

图6 各ZnO体系的透射光谱Fig.6 Transmittance spectra of every ZnO system

3 结论

本文采用基于密度泛函理论的第一性原理平面波超软赝势方法，对本征ZnO，Ga、F单掺ZnO，Ga-F共掺ZnO的几何结构进行优化并计算了各体系的相关性质。结果表明：Ga掺杂ZnO比F掺杂ZnO的晶格畸变小。富锌条件比富氧条件更有利于Ga原子和F原子进入ZnO的晶格，在相同环境下Ga原子比F原子更容易进入ZnO晶格，因此Ga掺杂ZnO体系比F掺杂ZnO更稳定。掺杂后费米能级进入导带，ZnO变为n型半导体，载流子浓度比本征ZnO提高了3个数量级，ZnO的导电性得到改善。相同浓度的F掺杂比Ga掺杂能产生更多的载流子。Ga-F共掺杂ZnO折中了上述Ga、F单掺杂ZnO的优缺点。另外相较于本征ZnO，掺杂ZnO的吸收边蓝移，在紫外光区的平均透射率增加。其中在280～380 nm范围内，3种掺杂体系的透射率均大于76%，Ga-F共掺杂ZnO的透射率最高，在90%以上。在制作TCO薄膜时可根据具体要求采取不同的掺杂方案以达到最好的效果。

致谢：非常感谢河北大学刘保亭教授为本文提供CASTEP计算软件并参与计算结果的讨论。

[1]ZHAO Xie-Qun(赵谢群).Electron.Compo.Mater.(电子元件与材料),2000,19(1):40

[2]LI Bao-Jia(李保家).Thesis for the Doctorate of Jiangsu University(江苏大学博士论文).2012.

[3]Estrich N A,Hook D H,Smith A N,et al.J.Appl.Phys., 2013,113(23):233703

[4]Gong L,Lu J,Ye Z.Sol.Energy Mater.Sol.Cells,2010,94 (6):937-941

[5]Guo J,Zheng J,Song X,et al.Mater.Lett.,2013,97:34-36

[6]Cao L,Zhu L P,Chen W F,et al.Opt.Mater.,2013,35(6): 1293-1296

[7]Nam G M,Kwon M S.Mater.Lett.,2011,7(2):127-131

[8]Choi B G,Kim I H,Kim D H,et al.J.Eur.Ceram.Soc., 2005,25(12):2161-2165

[9]Shi Q,Zhou K,Dai M,et al.Vacuum,2013,94:81-83

[10]Van de Walle C G,Neugebauer J.J.Appl.Phys.,2004,95 (8):3851-3879

[11]YU Pei-Qing(于培清).Thesis for the Masterate of Tianjin University(天津大学硕士论文).2010.

[12]LIU Jian-Jun(刘建军).Acta Phys.Sin.(物理学报),2010,59 (9):6466-6472

[13]ZHAO Dong-Qiu(赵冬秋).Thesis for the Masterate of Henan University(河南大学硕士论文).2008.

[14]LIU En-Ke(刘恩科),ZHU Bing-Sheng(朱秉升),LUO Jin-Sheng(罗晋生).Physics of Semiconductors.7th Ed.(半导体物理学.7版).Beijing:Publishing House of Electronics Industry,2011.

[15]YE Yu-Min(叶羽敏).Thesis for the Masterate of Zhejiang University(浙江大学硕士论文).2006.

[16]Sun F,Shan C X,Wang S P,et al.Appl.Surf.Sci.,2010, 256(11):3390-3393

[17]Terasako T,Ogura Y,Fujimoto S,et al.Thin Solid Films, 2013,549:12-17

[18]Zhang X,Zhu L,Xu H,et al.J.Alloys Compd.,2014,614: 71-74

[19]SHEN Xue-Chu(沈学础).Spectroscopy and Optical Properties of Semiconductors.2nd Ed.(半导体光谱和光学性质.2版).Beijing:Science Press,2002.

[20]FANG Rong-Chuan(方容川).Solid Spectroscopy(固体光谱学).Hefei:Press of University of Science and Technology of China,2001.

First-Principles Calculation on the Conductivity and Optical Transmittance of ZnO Codoped with Ga-F

HE Jing-Fang1,2WU Yi1SHI Ru-Qian1ZHOU Peng-Li1,2ZHENG Shu-Kai＊,1
(1Research Center for Computational Materials&Device Simulations,College of Electronic and Informational Engineering,Hebei University,Baoding,Hebei 071002,China)
(2School of Telecommunications Engineering,Xidian University,Xi′an 710071,China)

The related properties of intrinsic,Ga-,F-doped and Ga-F codoped ZnO are calculated after making geometry optimization using first principles plane-wave ultrasoft pseudopotential method based on the density functional theory.The results show that every doped ZnO has its own advantages and disadvantages,so there is different doping scheme according to specific requirement.The lattice distortion in Ga doped ZnO is smaller than F doped ZnO.And Ga doped ZnO has more stable structure than F doped ZnO,since Ga atoms are more likely to enter the ZnO lattice than F atoms under the same environment.Doping Ga and F improves the conductivity of ZnO.Compared with intrinsic ZnO,the carrier concentration of doped ZnO is increased by three orders of magnitude.And doping Ga can produce more carriers than doping F in the same concentration.Ga-F codoped ZnO reaches a compromise between merits and demerits of these properties above in Ga-doped and F-doped ZnO.In addition,the optical absorptions of doped ZnO generate a blue shift.The optical transmittance of Ga-F codoped ZnO is the biggest in ultraviolet region,and it is higher than 90%in 280～380 nm range.

ZnO;first-principles;carrier concentration;optical properties;optical transmittance

O649.4

A

1001-4861(2015)01-0015-08

10.11862/CJIC.2015.001

2014-04-14。收修改稿日期：2014-09-02。

国家自然科学基金(No.61306098)，国家留学基金(No.2014-3012)，河北大学大学生创新创业训练计划(No.2014038)资助项目。＊

。E-mail：zhshk@126.com