基于改进巴氏指标和模型更新的视觉跟踪算法

黄安奇，侯志强，余旺盛，刘 翔

（空军工程大学 信息与导航学院，陕西 西安710077）

引言

视觉跟踪问题是计算机视觉领域中的一个热点问题［1］。在各种各样的跟踪算法中，Mean Shift算法由于其计算复杂度低、稳健性较好和易于工程实现等优点已经广泛应用到各种实时跟踪系统中［2］。经典的 Mean Shift算法用Bhattacharyya系数进行相似度度量，但是 Khalid M.S.等人［3］发现应用巴氏指标对灰度图像进行匹配时存在偏差。应用传统的巴氏指标进行匹配存在偏差的根本原因在于背景特征的干扰。为了减少背景特征对目标定位的干扰，Liu［4］提出一种基于背景对照的相似度度量标准。Comaniciu［5］提出了背景加权直方图（background-weighted histogram）方法，随后国内外有很多基于背景加权直方图的改进算法被提出［6－7］。但是 Ning在文献［8］中经过理论推导和实验证明，文献［5］中的方法本质上与传统的Mean Shift算法是等价的，于是对其进行了修正，提出了修正的背景加权直方图（corrected background-weighted histogram）方法。该方法能够真正地降低目标模型中背景特征的概率。文献［9］同时利用了在线学习的目标及背景信息，能够较好地减少跟踪漂移问题。

Mean Shift算法由于本身缺少必要的模型更新策略，当场景中目标外观变化较大时，目标模型会逐渐漂移从而导致跟踪失败。目前针对Mean Shift算法中的模型更新问题，国内外都已经作了很多研究［10］，但是大部分更新算法只考虑了目标模型而忽略了背景模型。文献［11］通过引入背景模型提出了一种基于双模型判定的更新算法，有效区分了目标特征变化和短时遮挡对于跟踪的不同影响。

综合考虑以上算法的优缺点，本文提出了一种基于改进的巴氏指标和模型更新的视觉跟踪算法，从相似度指标和模型更新2个方面对传统的Mean Shift算法进行改进。首先通过引入前景／背景置信值对原始的巴氏指标进行改进，然后基于改进的巴氏指标，对目标与背景区域双模型相似度系数进行综合分析，准确地判断干扰目标匹配的原因，从而制定正确的模型更新策略。

1 传统的Mean Shift跟踪算法

Mean Shift跟踪算法［12］的基本思想是选择目标模型和候选模型的颜色直方图之间的相似度作为代价函数，通过梯度下降法迭代搜索代价函数的最大值。

目标模型的颜色直方图＾q＝｛＾qu｝u＝1，…，m表示为

类似于目标模型直方图，候选模型的颜色直方图＾p（y）＝｛＾pu（y）｝u＝1，…，m表示为

目标 模 型 的 颜 色 直 方 图 ＾p＝ ｛＾pu｝u＝1，…，m表示为

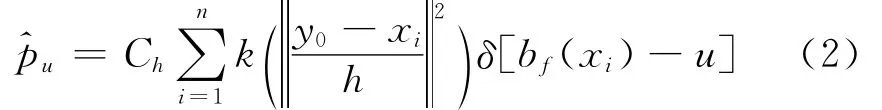
用Bhattacharyya系数来量测这2个模型的相似度，即目标模型和候选模型的相似度为

目标跟踪的关键就是寻找使得ρ（y）取得最大值的候选目标的位置，通过将ρ［＾p（y），＾q］在y0处展开，计算目标的新位置：

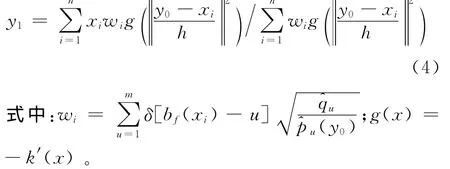
2 改进的巴氏指标

针对传统巴氏指标的不足，本文将基于背景直方图的前景／背景置信值引入到传统的巴氏系数中，这种改进的相似度指标能够有效地抑制背景干扰。

式中，η表示任意小的非零常数。从（5）式可知：如果颜色特征u在目标模型中是显著的，即＾qu≥＾ou，那么＾qu与＾ou的差值越大，颜色特征u所对应的置信值vu就越大。如果颜色特征u在背景区域是显著的，即＾qu＜＾ou，那么颜色特征vu所对应的置信值为0。因此，通过对前景特征突出的区域赋予较大的权值，对背景特征突出的区域赋予较小的权值或赋为0，从而有效地降低了目标模型中背景特征的概率，减少了背景特征对目标定位的干扰。

把vu带入传统的相似性度量 （3）式中得：

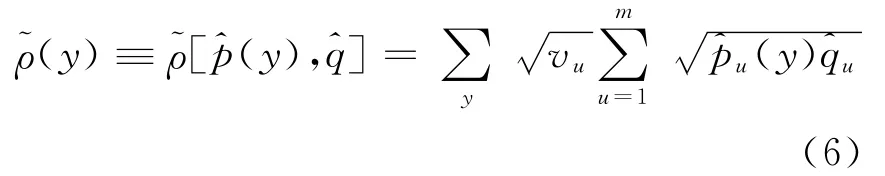
ρ˜（y）就是本文提出的一种将前景／背景置信值与Bhattacharyya系数相结合的相似度指标。定义新的权系数为＝，所以 （4）式可以写成：

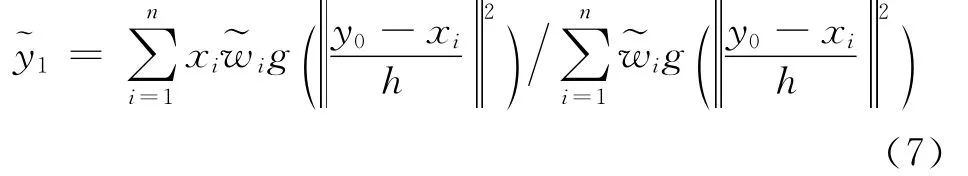
3 基于改进巴氏指标的模型更新策略

一个良好的模型更新策略需要解决2个问题：一是模型更新时机；二是模型更新准则。

3.1 模型更新时机

要确定模型的更新时机，必须判断导致模型发生变化的原因。通常目标和背景模型发生变化有以下几种情况：

1）背景特征基本不变而目标本身的特征发生了变化，如目标发生了平面外旋转。

2）发生了遮挡，目标的局部区域被背景中的非目标特征所覆盖。

3）由于目标的平移，导致跟踪场景中背景特征的改变，而目标的本身特征基本不变。

4）目标所处的场景整体发生变化。

目标和背景特征的变化通常是不同步的，由于背景变化的频繁性，本文算法中每一帧都对背景模型进行更新，然后通过对目标与背景双模型相似度系数进行综合分析，判断干扰目标匹配的原因，从而决定目标模型的更新时机。设当前帧的背 景 特 征 直 方 图 为 ｛＾o′u｝u＝1，…，m，置 信 值 为｛＾v′u｝u＝1，…，m，则当前帧的背景模型和前一帧的背景模型之间的相似度可以表示为

针对目标模型和背景模型设定2个相似度阈值ρt1和ρt2，对2个相似度系数进行综合分析确定目标模型的更新时机：

1）当ρ＞ρt1，ρo＞ρt2时，目标和背景都无明显变化，不对目标模型进行更新。

2）当ρ＞ρt1，ρo＜ρt2时，目标无明显变化，背景发生较大变化，不更新目标模型。

3）当ρ＜ρt1，ρo＞ρt2时，背景无明显变化，目标发生较大变化，此时需要对目标模型进行更新。

4）当ρ＜ρt1，ρo＜ρt2时，目标和背景都发生了较大变化。这可能是由2种情况导致的：一种情况是目标特征和背景特征都各自发生了变化；另一种情况是目标发生了遮挡。为了区别这2种情况，定义目标候选模型和背景模型的相似度为

设定ρ′的阈值为ρ′t。则当ρ＜ρt1，ρo＜ρt2且ρ′＞ρ′t时，说明大量的背景特征出现在了目标模型中，即发生了遮挡现象，此时不对目标模型进行更新；当ρ＜ρt1，ρo＜ρt2且ρ′＜ρ′t时，说明目标自身特征发生了变化，此时需要对目标模型进行更新。

3.2 模型更新准则

模型更新需要把握的基本准则就是，控制更新速度使其与目标特征变化相适应的同时抑制模型过更新。本文使用历史模型和当前模型进行加权来对目标模型实施更新：

式中：＾qt－1u、˜qtu分别为更新前后目标模型的颜色直方图；＾pu（y）为当前最佳候选区域的颜色直方图；a为模型控制因子，用来控制模型更新的速度，本文中a的取值范围是0.6～0.8。

考虑到背景变化的频繁性，本文在每一帧都使用当前帧的背景模型更新上一帧的背景模型：

4 算法步骤

在Mean Shift跟踪框架下，本文的改进算法完整描述如下：

步骤1 设定目标的初始中心位置为y0，按照（1）式计算目标模型的颜色直方图＾qu，按照（2）式计算候选模型的颜色直方图＾pu（y0）；

步骤2 根据（5）式和（6）式计算置信值及改进的相似度指标ρ˜（y0）；

步骤3 根据（7）式计算目标的新位置y1；

步骤4 计算新位置处的候选模型＾pu（y1）及其与目标模型的相似度ρ˜（y1）；

步骤5 若ρ˜（y1）＜ρ˜（y0），则令y1←—（y0＋y1）／2，并返回步骤4；

步骤6 若y0－y1＜ε，则转到步骤7；否则令y0← y—1，并返回步骤2；

步骤7 对3个相似度系数ρ、ρo和ρ′进行综合分析，采取正确的更新策略对目标模型和背景模型进行更新，然后继续下一帧的跟踪。

5 实验结果与分析

为了验证本文算法的有效性，将本文方法（ours）与目标的真实位置（ground truth）、原始的Mean Shift跟踪算法（MS）［12］、修正背景加权的 Mean Shift算法（CBWH）［8］、基于背景对照的 Mean Shift算法（BCKBT）［4］和利用偏最小二乘分析的目标跟踪算法（PLS）［9］进行比较，如图1、图2所示。为便于对比和分析，且保持结论的一般性，几种算法都不考虑尺度变换。本文的仿真环境为：Intel G1610CPU，2G内存，Windows XP系统，MATLAB 7.12.0。

图1 跟踪算法性能的定性比较Fig.1 Qualitative comparison among 4 tracking algorithms

5.1 定性分析

实验1 采用Takeoff序列，由图1（a）的跟踪结果可以看到：1）原始的MS算法很快丢失目标。2）CBWH算法和BCKBT算法随着目标逐渐变小，跟踪窗口开始出现偏移并最终丢失目标。PLS算法在背景特征变化时，跟踪结果同样出现了偏差。3）本文算法在整个跟踪过程中都保持着稳定的跟踪能力。

实验2 采用Airplane序列，由图1（b）的跟踪结果可以看到：1）原始的MS算法很快便丢失目标。2）CBWH算法对于背景特征的剧烈变化不能很好地适应，在345帧～676帧丢失目标。3）相比CBWH算法，BCKBT算法和PLS算法能够更好地抑制背景特征的影响，在整个跟踪过程中未丢失目标。4）以上4种算法在跟踪过程的最后阶段，由于机身颜色的变化，跟踪窗口都出现严重偏移。而本文算法在整个跟踪过程中都保持着较好的跟踪性能。

实验3 采用Trellis视频序列，由图1（c）的跟踪结果可以看到：1）原始MS算法的跟踪窗口偏移真实位置较远。2）CBWH算法和BCKBT算法同样由于缺少必要的模型更新机制，跟踪结果误差较大。PLS算法在光照变化剧烈时多次丢失目标。3）本文算法则能根据目标的外观变化，不断将当前目标中新出现的颜色分量更新到目标模型中，跟踪性能明显提高。

实验4 采用Girl视频序列，由图1（d）的跟踪结果可以看到：原始的MS算法、CBWH算法和BCKBT算法由于缺少必要的模型更新机制，跟踪结果误差较大。PLS算法能够对目标模型进行较好地更新，但是由于不具有遮挡判断机制，在遮挡发生时将遮挡物的特征更新到了目标模型中，最终导致跟踪失败。本文算法由于制定了有效的模型更新策略，能够及时地将目标中新出现的特征更新到目标模型中。同时由于采取了灵活的遮挡判断机制，在发生遮挡时能够自动停止对模型的更新，使得算法具备较好的鲁棒性。

5.2 定量分析

本文对以上4种算法的跟踪性能进行了定量对比。图2为跟踪结果中心点与目标真实中心位置的误差，真实位置通过手工标注得到。本文算法的中心位置误差最小。

为了分析算法的实时性，表1给出了5种算法跟踪各组视频序列时，处理一帧所需的时间（单位：ms，粗体为最优结果，粗斜体为次优结果。）可以看出，本文算法虽然涉及相似度指标的改进和模型更新，但由于提高了跟踪精度，从而减少了Mean Shift迭代次数，实时性较好，仅次于原始的Mean Shift跟踪算法。

表1 跟踪算法实时性比较（时间／ms）Table 1 Real-time performance of these algorithms

6 结论

针对传统Mean Shift算法所采用巴氏指标的缺陷以及缺少有效的模型更新策略的问题，本文提出了一种基于改进的巴氏指标和模型更新的视觉跟踪算法，从相似度指标和模型更新2个方面对传统的Mean Shift算法进行改进。实验结果表明，该算法能够有效地抑制背景干扰和进行模型更新，最终获得了更为鲁棒的跟踪性能。

［1］ Wu Y，Lim J，Yang M H.Online object tracking：a benchmark［C］.Portland，United Stater：Proc.of Computer Vision and Pattern Recognition，2013：2411-2418.

［2］ Yang C J，Duraiswami R，Davis L.Efficient meanshift tracking via anew similarity measure［C］.San Diego：Proc.of Computer Vision and Pattern Recognition，2005：176-183.

［3］ Khalid M，Malik M.Biased nature of Bhattacharyya coefficient in correlation of gray-scale objects［C］.Zagreb Croatia：International Symposium on Image and Signal Processing and Analysis，IEEE，2005：209-214.

［4］ Liu Rongli，Jing Zhongliang.Robust kernel-based tracking algorithm with background contrasting［J］.Chinese Optics Letters，2012，10（2）：021001.

［5］ Comaniciu D，Ramesh V，Meer P.Kernel-based object tracking［J］.IEEE Transactions on Pattern A-nalysis and Machine Intelligence，2003，25（5）：564-577.

［6］ Jeyakar J，Babu R，Ramakrishnan K R.Robust object tracking with background-weighted local kernels［J］.Comput.Vis.Image Underst.，2009，112（3）：296-309.

［7］ Chen Aibin，Cai Zixing，Dong Deyi.A tracking method based on weighted object and background［J］.Control and Decision，2010，25（8）：1246-1250.陈爱斌，蔡自兴，董德毅.一种基于目标和背景加权的目标跟踪方法［J］.控制与决策，2010，25（8）：1246-1250.

［8］ Ning J，Zhang L，Zhang D，et al.Robust mean shift tracking with corrected background-weighted histogram［J］.IET Computer Vision，2012，6（1）：62-69.

［9］ Wang Q，Chen F，Xu W L，et al.Object tracking via partial least squares analysis［J］.IEEE Transactions on Image Processing，2012，21（10）：4454-4465.

［10］Matthews I，Ishikawa T，Baker S.The template update problem［J］.IEEE Transactions on Pattern A-nalysis and Machine Intelligence，2004，26（6）：810-815.

［11］Qin Jian，Zeng Xiaoping，Zeng Hao.Dual template algorithm for mean-shift template update［J］.Application Research of Computers，2009，26 （7）：2771-2774.覃剑，曾孝平，曾浩.均值漂移跟踪的双模板更新算法［J］.计算机应用研究，2009，26（7）：2771-2774.

［12］Comaniciu D，Ramesh V，Meer P.Real-time tracking of non-rigid objects using mean shift［C］.Hilton Head Island，USA：Proc.of Computer Vision and Pattern Recognition，2000：142-149.