线性判别分析的迭代解法及其应用❋
张建文, 刘新国
(中国海洋大学数学科学学院,山东 青岛 266100)
线性判别分析的迭代解法及其应用❋
张建文, 刘新国
(中国海洋大学数学科学学院,山东 青岛 266100)
线性判别分析(LDA)作为一种降维技术,已成功应用于许多分类问题中,如语音识别、人脸识别、信息提取等领域。本文研究并改进求解迹比问题的两种主要方法:二分法、迭代迹比法(ITR法)。主要研究成果有:给出了一种基于线性插值的求解非线性方程二分法的改进算法;对这两种迭代方法与基于比迹准则的方法进行比较;对于ITR算法,选择好的初始迭代矩阵使得算法的收敛速度有明显的提高;分析了组内样本的相关性对识别精度的影响。
线性判别分析;迭代解;迹比问题
线性判别分析(LDA)是一种重要的统计学方法上的一种分析方法,已经广泛应用于医学的患者疾病分级以及人脸识别、模式识别、文本分类等领域。

针对小样本问题以及由数据维数高带来的计算复杂性问题,近年来提出了很多基于LDA的判别分析方法,包括PCA+LDA[7,9-10],正则化LDA[8],广义逆LDA,LDA/GSVD[11]等。这些方法均是基于比迹准则而设计的。
Guo[12]通过广义变换提出迹比问题和迹差分问题,给出了一种基于二分法的迭代算法。但是该算法收敛较慢,且不稳定。Wang提出了一种更为有效的算法[13](ITR算法),该算法稳定,收敛较快。近期还提出了ITR算法的改进[14-16]。
本文研究迹比问题的求解及应用,所做的主要工作包括以下几个方面:
(1)选择好的初始迭代矩阵提高ITR算法精度和速度;
(2)分析组内相关性对算法精度的影响;
(3)针对高维数据,对算法进行了改进,提高了效率。
1 线性判别分析
给定一个样本数据矩阵A∈Rm×n,寻找一个线性变换WT∈Rl×m,使得A的每一列ai,从m维空间中映射到l维空间中,即
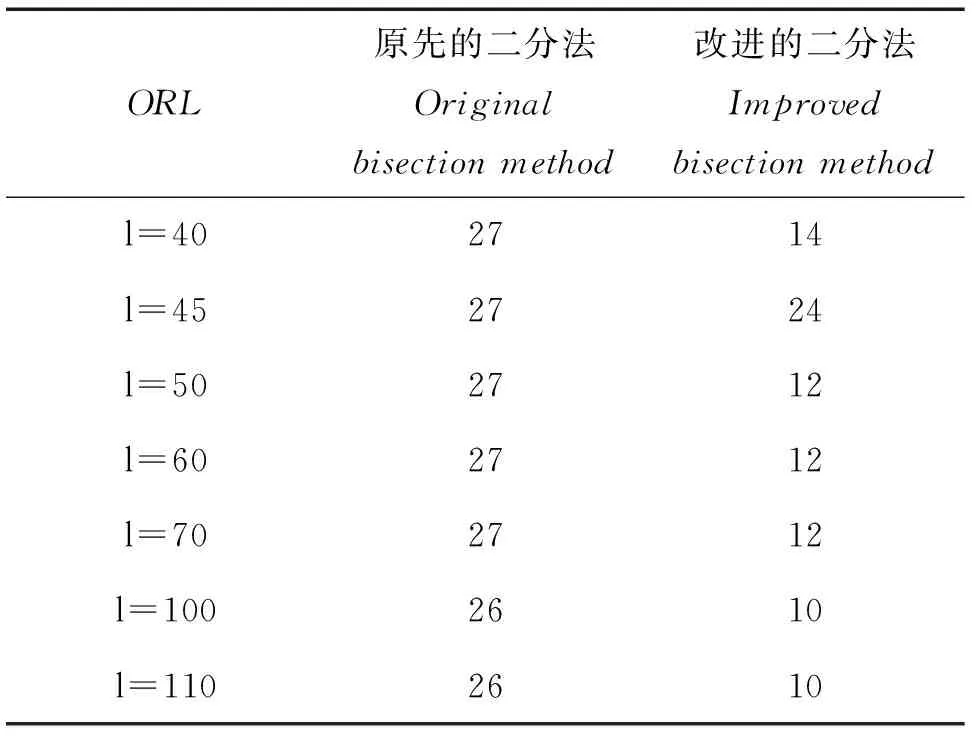
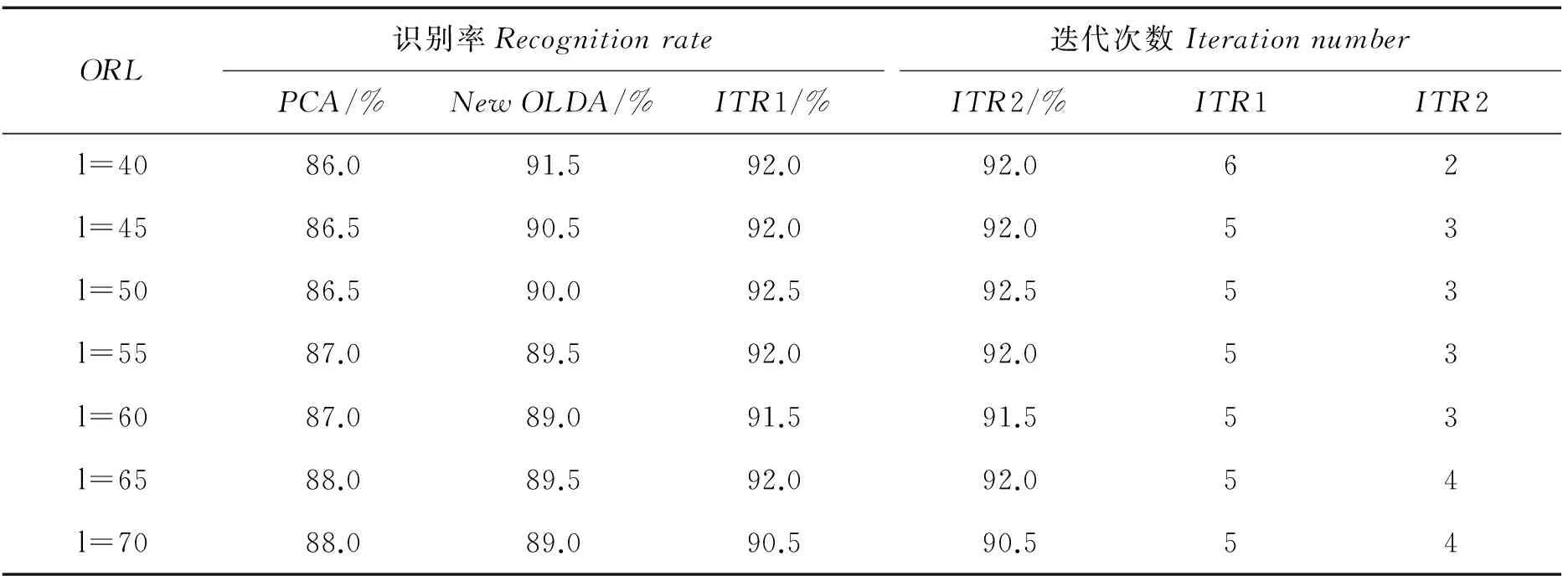
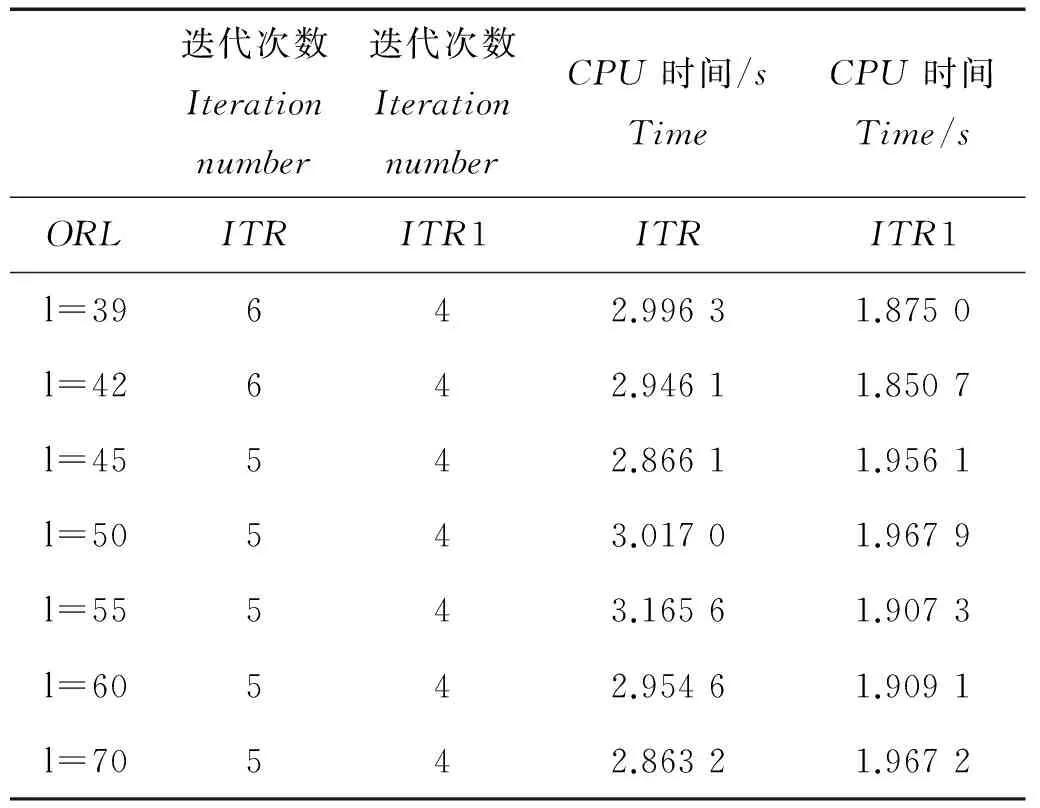
WT:ai∈Rm→yi=WTai∈Rl,l< 设样本数据矩阵A分为k类, 在判别分析中,定义如下3个矩阵,分别为类间、类内、总体散度矩阵: 显然,上述3个矩阵满足以下关系式: St=Sw+Sb。 经过线性变换,在低维空间中可以得到类间、类内、总体散度矩阵为 给定2个半正定矩阵Sp∈Rm×m,Sl∈Rm×m,比迹问题就是寻找一个m×l(l (1) 当Sp=Sb,Sl=Sw时,(1)就是经典的LDA问题。 这一问题可以通过求解广义特征值问题Sbwk=βkSwwk得到解决。其中βk是第k个最大的广义特征值,矩阵W是由前l个最大特征值对应的特征向量构成。 本文要讨论的是求解以下迹比最优化问题: (2) 定理2.1[12]迹比问题等价于求解下述迹差分问题: 求迹差分函数的零点λ* 即f(λ*)=0,则可以由下式计算: 定理2.2[12]假设A为实对称矩阵,则满足 其中λ1≥λ2≥…≥λm为A的m个特征值。假如φ1,φ2,…,φm为λ1,λ2,…,λm对应的单位正交特征向量,则有 由以上定理可知,求解迹比问题可转化为求解迹差分问题。 2.1 对二分法收敛速度的改进 Guo等在文献[12]中提出了一种基于二分法的迭代方法,与基于比迹准则的方法相比较,识别率有明显提高。但是,二分法的收敛速度较慢,要求的精度越高,需迭代的次数也越来越多,所以此方法须进一步改进。 文献[17]提出了一种基于线性插值的求解非线性方程二分法的改进方法,其基本思想是在每进行一次平分隔根区间后,接着进行一次线性插值,然后根据插值得到的点处的函数值与中点处的函数值进行比较,可以得到有根区间,由此取得的区间均小于基于二分法取得的区间,从而加快了收敛速度。 结合文献[17]以及本文问题,给出改进的二分法,具体算法如下: 算法2.1 (i)令λ1=0,λ2=1,λ=(λ1+λ2)/2; (iii)计算f(λ1),f(λ2),f(λ); (1)若f(λ)<0,对点λ1与λ进行线性插值,则得到直线与x轴的交点c,其表达式为: (2)若f(λ)>0,对点λ2与λ进行线性插值,则得到直线与x轴的交点c,其表达式为: (iv)λ*=λ; 从而W为Sb-λ*St的前l个最大特征值对应的特征向量组成。 2.2ITR方法 Wang在文献[13]提出一种有效算法(ITR),简要概述如下: 算法2.2 (i)初始化W为任意的列正交矩阵; (iii)构造迹差分问题 (iv)W*是由Sb-λSt的前l个最大特征值对应的特征向量构成,用W*更新W; (v)迭代(ii)-(iv),直至收敛。 2.2.1 初始点策略 前述ITR算法选取任意的列正交矩阵为初始点。我们选取比迹问题的解作为ITR的初始迭代矩阵。数值实验结果表明,这一策略可以提高ITR的收敛速度,具体结果见实验部分。 2.2.2 组内相关性对算法精度的影响 训练样本集A=[A1,…,Ak],Ak代表一个子类。如果分类较精确,则Ai的列向量几乎线性相关,样本之间的特征差异不明显,不能有效的表征类别信息。从训练集表征的角度来看,样本选择可以有效的精简训练集,去除相似、重复、噪声、以及信息冗余的样本,实现以小规模样本子集来表征整体训练集分布。子空间样本选择算法如下[18]: 算法2.3 设样本包含S个样本,已选样本集Sl,l是已选择样本数,S=[x1,…,xn]。 (ii)对于∀xp∈S/S1,计算xp到子空间的距离平方d2(xp,span(S1))。则 令mxd=d2(zl+1,span(S1))。 (iii)若mxd>ε,则Sl=S∪zl+1,更新l=l+1;否则退出。 (iv)返回(ii),迭代(ii)-(iii),直至l=m。 由文献[18]可知,问题最终可以转化为 d2(xp,span(S1))=(xp,xp)-kTK-1k。 k=((z1,xp),(z2,xp),…,(zl,xp))T。 上述选择方法不仅能够很好的反映样本分布,而且使得选择的样本对其他样本的重构误差迅速减少,选择的样本是线性无关的。 由于矩阵S与λ有关,因此所有的特征值与特征向量实际上是关于λ的函数,所以把它们写做λ的函数βi(λ),wi(λ)更合适。 引理2.1[14]如果β(λ)为S(λ)=Sb-λSt的单特征值,w(λ)为对应的单位特征向量(w(λ)=1),则特征值的导数为 β′(λ)=-wT(λ)Sbw(λ)≤0。 (3) 引理2.1可以使用一阶泰勒展开式来估计βk在λt处的特征值。 (4) (5) Jia在文献[14]中给出了该方法的算法流程。 算法2.4 (i)初始化λt=0,t=0; (ii)Sb-λtSt的特征值分解; (iii)计算(4)(5)式; 该算法与ITR算法不同之处在于步骤(iv),ITR算法是选取矩阵Sb-λSt最大的l个特征值对应的特征向量,然而f(λ)=0的解并不一定是由这l个特征向量组成。因此,本算法在每一次迭代过程中得到的迹比值λ往往要大于ITR算法所得,收敛更快。 因为涉及含未知量的排序,该算法的实现比较困难。结合文献[15-16,19],针对步骤(iv),设计算法2.5如下: (iii)按降序排列score(i),i=1,2,…,m; (iv)取前l个最大的score(i)对应的向量wi,组成W=[wi1,wi2,…,wil]; (vi)λ0=λ1; 从上面可以看出,该算法无需计算特征值分解,且相对于特征值分解而言,计算量可以忽略。 本文使用ORL人脸库和YALE人脸库来测试算法性能。ORL人脸库由剑桥大学ATT实验室创建,包含40人,共400张面部图像,尺寸大小为112×92像素大小。为便于计算,大小选为56×46,选取200张为训练集,余下为测试集。YALE人脸库包含15位志愿者的165张人脸图像,每人各有11幅图像,尺寸为320×243像素大小。采用的分类方法为3阶近邻分类法(3-NearestNeighbor)。 3.1 改进前后二分法收敛速度比较 从表中可以看出,在相同的误差范围内,改进后的二分法要比之前的二分法迭代的次数明显减少,收敛速度比较快,说明了该方法的有效性。 3.2 初始迭代矩阵的选择对精度的影响 表1 算法的收敛速度比较(迭代次数) (1)基于迹比最优化准则的识别率要高于基于比迹最优准则,同时也说明了比迹问题的最优解并不是迹比问题的最优解; (2)选择好的初始迭代矩阵使得算法的求解速度有明显的提高。 3.3 组内相关性对精度的影响 实验选用2组数据:ORL人脸库,大小为56×46,从每组10个样本中选取5个为训练集,余下为测试集;YALE人脸库,大小为64×64,从每组11个样本中选取5个为训练集,其余6个为测试集(ITR1表示随机选择样本,ITR2表示选择样本后的ITR算法)。 表2 不同初始迭代矩阵对识别率与迭代次数的影响 表3 样本相关性对精度的影响 从表中可以看出,样本的相关性对识别精度有重要的影响。选择线性无关的样本,将会提高识别率,特别是对于大规模数据集的样本识别中,识别样本个数增多,存储矩阵所需的内存空间要求也增加。因此,用尽可能少的样本来取得更高的效率,显得极为重要,这就需要筛选好的样本组成训练集。 3.4 改进前后的ITR算法判别性能比较 虽然二种算法的识别率是一样的,但是从表中可以看出,改进后的ITR算法(ITR1)的迭代次数比ITR算法少,CPU花费时间也明显少于ITR算法。说明改进后的ITR算法的收敛速度高于ITR,效率更高,优于ITR算法。 表4 收敛速度的比较 本文针对二分法收敛较慢的问题,在每次迭代之后增加了一次线性插值,提高了其收敛速度。分析了初始迭代阵的选择、组内样本相关性对ITR算法精度的影响,给出了改进后的ITR算法,并取得了很好的识别效果。 [1] Fisher R A.The use of multiple measurements in taxonomic problems [J]. Ann Eugenics, 1936: 178-188. [2] Sammon J W. An optimal discriminant plane [J]. IEEE Trans Comput, 1970, 19: 826-829. [3] Foley D H, Sammon J W. An optimal set of discriminant vectors [J]. IEEE Trans. Comput, 1975, 24(3): 281-289. [4] Tian Q. Image classification by the Foley-Sammon transform [J]. Opt Eng, 1986, 25(7): 834-839. [5] Hong ZQ. Algebraic feature extraction of image for recognition [J]. Pattern Recognition, 1991, 24(3): 211-219. [6] Liu K, Cheng Y Q, Yang J Y. An efficient algorithm for Foley-Sammon optimal set of discriminant vectors by algebraic method [J]. Int J Pattern Recognit Artif Intell, 1992, 6(5): 817-829. [7] Sweet D L, Weng J. Using discriminant eigenfeatures for image retrieval [J]. IEEE Transaction on Pattern Analysis and Machine Intelligence, 1996, 18(8): 831-836. [8] Friedman J H. Regularized discrimination analysis [J]. Journal of the American Statistical Association, 1989, 84(405): 165-175. [9] Belhumeur P N, Hespanha J P, Kriegman D J. Eigenfaces vs FIsherfaces:recognition using class specific linear projection [J]. IEEE Transaction on Pattern Analysis and Machine Intelligence, 1997, 23(2): 711-720. [10] Howland P, Park H. Equivalence of several two-stage methods for linear discriminant analysis [C]. Florida: Fourth SIAM International Conference on Data Mining, 2004. [11] Howland P, Jeon M, Park H. Structure preserving dimension reduction for clustered text data based on the generalized singular value decomposition [J]. SIAM J Matrix Anal Appl, 2003, 25: 165-179. [12] Guo Y, Li S, Shu T, Wu L. A generalized Foley-Sammon transform based on generalized fisher discriminant criterion and its application to face recognition [J]. Pattern Recognition Letters, 2003, 24(1): 147-158. [13] Wang H, Yan S, Xu D, Huang T S. Trace ratio vs ratio trace for dimensionality reduction [J]. Proceeding of conference on Computer Vision and Pattern Recognition(CVPR), 2007: 1-8. [14] Jia YQ, Nie F P, Zhang C S. Trace ratio problem revisited [J]. IEEE Transactions on Neural Networks, 2009, 20(4): 729-735. [15] Nie FP, Xiang SM, Jia Y Q, Zhang C S. Semi-supervised orthogonal discriminant analysis via label propagation [J]. Pattern Recognition, 2009, 42: 2615-2627. [16] Nie F P, Xiang S M. Trace ratio criterion for feature selection [C]. Chicago: Proceeding of the Twenty-Third AAAI Conference on artificial Intelligence, 2008: 671-176. [17] 王国栋, 张瑞平, 沐爱勤, 等. 基于线性插值的求解非线性方程二分法改进 [OL]. 中国科技论文在线, http://www.paper. edu. cn/releasepaper/content/200904-657. [18] 周晓飞, 姜文瀚, 杨静宇. 基于子空间样本选择的最近凸包分类器 [J]. 计算机工程, 2008, 34(12): 167-168. [19] Zhao M B, Zhang Z, Chow W S. ITR-Score algorithm: an efficient trace ratio criterion based algorithm for supervised dimensionality reduction [C]. Portland: Proceeding of International Joint conference on Neural Networks, 2011: 145-152. [20] Ye J. Characterization of a family algorithm for generalized discriminant analysis on undersampled problems [J]. J Mach Learn Res, 2005, 6: 483-502. [21] Chu D L, Goh S T. A new and fast orthogonal linear discriminant analysis on undersampled problems [J]. SIAM J SCI Comput, 2010, 32(4): 2274-2297. [22] 谢达东, 吴及, 王作英. 线性判别分析在汉语语音识别中的应用 [J]. 计算机工程与应用, 2003, 23: 1-8. [23] 胡煜. 线性判别分析和降维方法应用于基因芯片数据分析 [J]. 甘肃联合大学学报(自然科学版), 2008, 22(1): 29-33. [24] 鲁晓春, 施先亮. 应用Fisher线性判别分析法评估物流规划项目 [J]. 分析与决策, 2007, 26(8): 76-79. AMS Subject Classification: 93B05 责任编辑 陈呈超 The Iterative Solution of Linear Discriminant Analysis and Its Application ZHANG Jian-Wen,LIU Xin-Guo (School of Mathematical Sciences, Ocean University of China, Qingdao 266100, China) Linear discriminant analysis(LDA) has been successfully used as a dimensionality reduction technique to many classification problems,such as speech recognition,face recognition and information retrieval.We study some efficient iterative procedures to directly solve the trace ratio optimization problem,namely,bisection method,iterative trace ratio.We made some improvements to these methods.The main research achievement are as follows:we present an improved bisection method based on linear interpolation for solving nonlinear equation;we compare these two methods against ratio trace solution to LDA;for the ITR algorithm,a good choice of initial iterative matrix makes the convergence speed of our method improved significantly;we analyze the influence of the correlation of sample to recognition accuracy. linear discriminant analysis;iterative solution; trace ratio problem 国家自然科学基金项目(11371333)资助 2013-07-10; 2014-01-15 张建文(1987-),男,硕士生。E-mail:ahzhang1108@163.com O212.5 A 1672-5174(2015)11-119-06 10.16441/j.cnki.hdxb.20130328
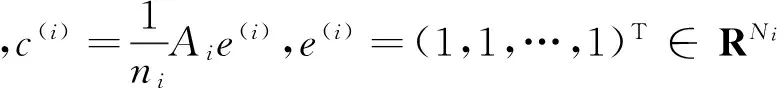
2 线性判别分析的迭代解法及其改进

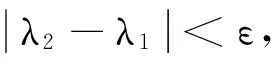
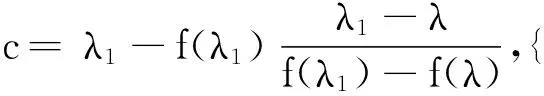
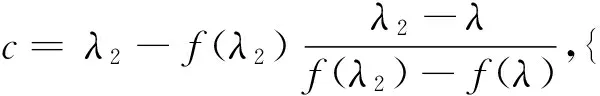
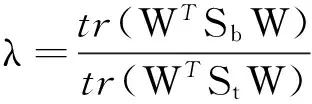

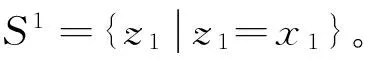
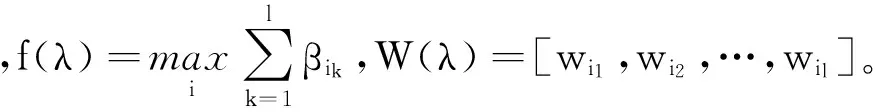
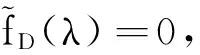
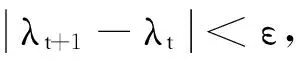
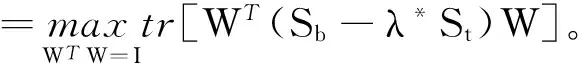




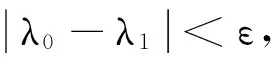
3 实验结果与分析
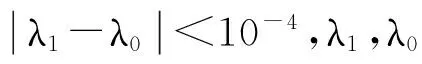

4 结语

