波浪作用下粉质土海床累积孔隙水压力简化分析❋

王 虎， 刘红军,2

(中国海洋大学 1. 海洋环境与生态教育部重点实验室； 2. 环境科学与工程学院， 山东 青岛 266100)



波浪作用下粉质土海床累积孔隙水压力简化分析❋

王 虎1， 刘红军1,2

(中国海洋大学 1. 海洋环境与生态教育部重点实验室； 2. 环境科学与工程学院， 山东 青岛 266100)

波浪引起的孔隙水压力直接影响海床地基稳定性，而累积孔隙水压力是细颗粒弱粘性粉质土的主要响应形式。针对在海岸和近海广泛分布的粉质土，基于一维固结理论，采用更适于描述粉质土动力特性的双曲线型孔隙水压力发展模式作为源项，推导相应的有限差分格式，并在MATLAB环境下进行编程求解，给出波浪作用下粉质土海床累积孔隙水压力响应的简化分析方法。以黄河三角洲为背景的算例显示，本文所给的模型和计算方法高效、易行，可为相关的海岸与海洋工程设计提供理论参考和技术支持。

波浪荷载；粉土；累积孔隙水压力；固结方程；有限差分；黄河三角洲

波浪作用下孔隙水压力的发展变化直接影响海床地基稳定性，威胁海洋工程的安全稳定和正常使用[1-2]。例如，以粉质土为代表性土类的黄河三角洲地区[3-4]，广泛发育有海底滑坡、塌陷凹坑、粉砂流冲沟等海底地质灾害和灾害地貌[5-6]，曾发生海底电缆弯折[3]和平台失稳[7]的案例。研究表明，风暴潮伴随的极端波浪与粉质土海床相互作用所引起的孔隙水压力变化是上述地质灾害和海洋工程失稳的重要诱因[3,7-8]。粉质土介于砂土和黏土之间，具有相对特殊的物理性质和静、动力学性质，且在海岸和近海地区广泛分布[9]，因此，研究波浪作用下粉质土海床的孔隙水压力响应具有重要意义。

波浪作用下海床孔隙水压力响应有瞬态和累积两种机制：瞬态孔隙水压力围绕平衡位置往复振荡，累积孔隙水压力从初始值累积升高[1-2]。瞬态机制多对应于较小的波浪与较大刚性的粗颗粒土组合；而对于极端波浪与细颗粒弱黏性粉质土的组合，累积机制则占主导地位[2]。室内水槽试验[10]和现场试验[11]均发现波浪引起细粒土海床中明显的孔隙水压力累积升高。

波浪作用下海床累积孔隙水压力的计算方法中，二维弹塑性模型[12]的参数获取和计算实现较为复杂，简便易行的是将其简化为一维问题，以带源项的一维固结方程作为控制方程，将基于土的动力试验获得的孔隙水压力发展模式作为源项，将波浪循环荷载作为唯一外荷载，研究竖向海床孔隙水压力随时间的发展变化[2,13-17]。孔隙水压力发展模式因土体自身状态及所施加外荷载的不同而具有多种形式，当前已被应用于计算的有经典的砂土反正弦型[13]、简化的线性型[7,14-15]、考虑砂土主应力旋转[16]及考虑加载历史[17]的发展模式。研究表明，双曲线型的孔隙水压力发展模式更适于描述粉质土的动力响应[9,17-20]，但目前为止，鲜见应用双曲线型发展模式计算波浪作用下海床累积孔隙水压力的相关研究。

鉴于此，本文基于一维固结理论，采用双曲线型的孔隙水压力发展模式作为源项，推导有限差分格式，在MATLAB环境下实现编程求解，建立一种波浪作用下粉质土海床累积孔隙水压力响应的简化分析方法。以黄河三角洲为例，应用现场的波浪参数和土层土性参数，研究波浪作用下粉质土海床的累积孔隙水压力响应，并讨论其响应机制。

1 基本方程

海水覆盖的海床是由土颗粒和孔隙水组成的典型固、液两相饱和土，适用于经典的Tergazhi一维渗流固结理论[21]。一维情况下的Biot固结方程与Terzaghi固结方程具有相同的形式，该方程建立在以下假设之上：土体均质各向同性，线弹性，小变形，渗流符合达西定律。将该方程作为波浪作用下海床累积孔隙水压力响应的控制方程，表达式为：

(1)

式中：u为累积孔隙水压力；t为时间；cv为土的固结系数；z为海床深度(海床表面为零，向下为正方向)；f为源项即孔隙水压力发展模式。式(1)这一形式的方程是一种典型的抛物线型偏微分方程，也被用于研究热传导或有源扩散问题。

假设海床表面自由排水，无限深海床底部刚性隔水；海床各层之间满足孔隙水压力连续和流速连续条件；波浪作用之前整个海床的累积孔隙水压力为零。边界条件、层间连续条件和初始条件表示为：

(2)

(3)

u(z,0)=0。

(4)

式中：k为渗透系数；i为土层编号。

孔隙水压力发展模式及其参数的选取，直接影响到计算的准确性[18]。本文采用刘红军等[20]建立的黄河三角洲粉质土的双曲线型孔隙水压力发展模式：

(5)

式中：σ0’为初始竖向有效应力，可通过σ0’=γ；z计算；γ；为土体浮容重；N为动荷载循环次数；Nl为累积孔隙水压力达到液化或稳定时的循环次数，a、b、c为经验系数。N和Nl的表达式[14]为：

(6)

(7)

式中：T为波浪周期；α、β为与土的类型及相对密度相关的参数；τ为波浪引起的海床内剪应力幅值。联立式(5)、(6)，孔隙水压力发展模式f可写成：

(8)

式(7)中波浪引起的剪应力幅值τ，采用Biot方程计算，并且假设孔隙水压力累积过程中τ不变[2,13-17]。当海床深度大于半个波长之时，τ的表达式为：

τ=P0λzexp(-λz)。

(9)

式中：λ为波数(λ=2π/L)；L为波长；P0为床面动水压力幅值：

(10)

式中：γw为海水容重；H为波高；d为水深。联立式(7)～(10)可得f的表达式，再结合式(1)～(4)，构成波浪作用下海床累积孔隙水压力响应初边值问题的基本数学表达。

2 有限差分求解及验证

采用有限差分法对初边值问题进行求解，在平面区域z-t方向做矩形网格剖分，h=z/M，Δt=t/N分别为空间和时间步长，M、N分别为空间和时间步数。采用具有二阶精度并且无条件稳定的Crank-Nicolson差分格式进行离散，表示如下：

(11)

为方便起见，将网格比记为：

(12)

对式(11)进行整理，得到由第k时间层向第k+1时间层计算累积孔隙水压力的三对角方程组：

(13)

此方程组系数矩阵严格对角占优，存在唯一解，在MATLAB环境下编程求解。

若式(1)不含源项f，则退化为经典的Terzaghi一维固结方程，为验证本文差分格式和求解程序的有效性，将退化方程的差分解与解析解[21]进行比较，参数取为：均质土层厚度z=20m，表层单面排水，表面瞬时均布荷载100kPa，即整个土层的初始超孔隙水压力值u0=100kPa，固结系数Cv=0.002 m2/s，取10000s时的超孔隙水压力值输出，如图1所示，二者具有较好的一致性。

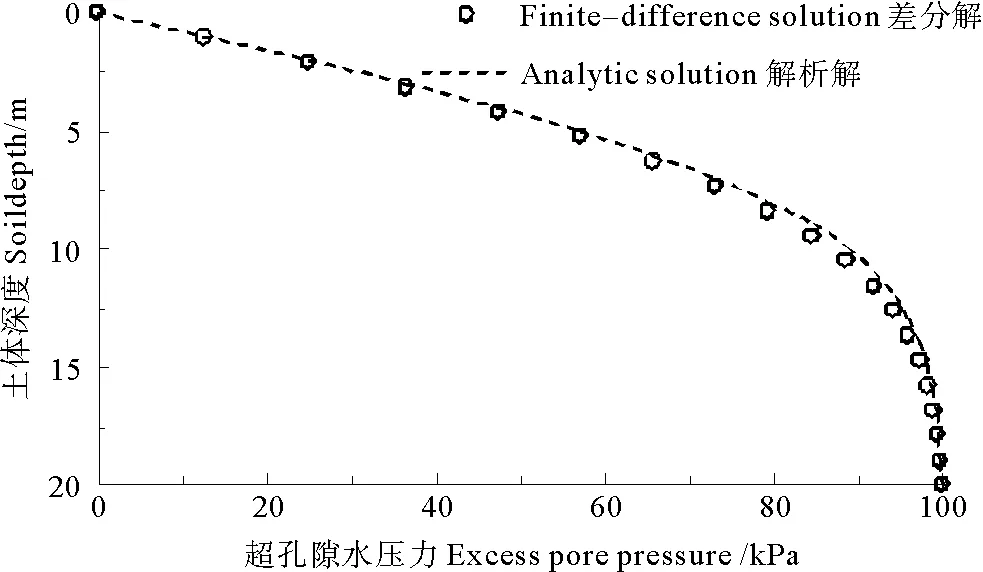
图1 差分解与解析解比较

3 波浪作用下黄河三角洲粉质土海床累积孔隙水压力响应

以黄河三角洲埕岛海域为背景，计算中考虑了不同水深条件下5年一遇和50年一遇2种类型的波浪[7-8,12]，如表1所示。计算中采用了粉砂、粉土、粉质黏土3种类型的均质海床，同时研究了文献[4]所述的上部有2m厚度的粉土硬壳层，下部为粉质黏土的地层组合，简称为“双层海床”。计算中海床厚度取为40m，以保证其大于半个波长从而剪应力幅值满足式(9)，空间步长取为0.5m。时间步长取为1s，参照风暴潮的持续作用时间，最长计算到120min。参照文献[7,12,21]得到土体浮容重和固结系数，根据文献[20]得到孔隙水压力发展模式的参数。根据文献[2,14-15]，公式(7)中参数取为α=0.246，β=-0.165。海床土参数详见表2。

表1 波浪参数

Note： ①Water depth；②Ware with recarrence interval of fifty years；③Ware height；④Ware length；⑤Period

表2 海床土体参数

Note： ①Soil kind；②Submergedanit weight；③Wefficient of consolidation；④Parameter of poe water presult decpment model；⑤Sandy cilt；⑥Silt；⑦Silty clay

图2(a)给出了10 m水深50年一遇波浪作用下均质粉土海床的响应，累积孔隙水压力随着时间增加不断增大，其最大值约为40 kPa，出现在床面以下15 m左右。岩土工程师所关注的一个焦点是超孔隙水压力与初始竖向有效应力的比值，即超孔隙水压力比(u/σ0’)，u/σ0’越大海床失稳破坏的可能性越大。图2(b)给出10 m海床深度范围内u/σ0’的变化情况，可以看出u/σ0’在海床表层附近最大，最大值超过0.8，随着深度的增加而逐渐减小，在10 m处已不足0.4，但均未超过1。

图3给出了不同水深条件下50年一遇波浪作用60 min均质粉土海床的响应，累积孔隙水压力随着水深的增加不断增大，8和10 m的累积超孔隙水压力基本相等，表明在水深增大到8～10 m时50年一遇波浪对粉土海床的影响已达到最大。

图4给出了不同波浪作用60min时10m水深均质粉土海床响应，可以看出波浪条件越极端，累积孔隙水压力越大。

(10 m水深50年一遇波浪条件下均质粉土海床响应：(a)累积孔隙水压力；(b)超孔隙水压力比。for the case of homogeneous silty seabed under 50-year once wave with 10 m water depth: (a) residual pore pressure along depth; (b) excess pore pressure ratio along depth.)

图2 时间对累积孔隙水压力的影响
Fig.2 Effects of time on residual pore pressure response

(50年一遇波浪作用60 min均质粉土海床响应。(for the case of homogeneous silty seabed under 50-year once wave with duration of 60 min,)

图3 水深对累积孔隙水压力的影响
Fig.3 Effects of water depth on residual pore pressure response

图5为10m水深粉砂、粉土、粉质黏土3种均质海床以及双层海床在50年一遇波浪作用60min时的累积孔隙水压力曲线。从图中可以看出，均质粉土和粉质黏土海床的孔隙水压力累积幅度大致相等，粉质黏土海床的累积孔隙水压力最大值出现的深度略大于粉土海床。均质粉土和粉质黏土的孔隙水压力累积幅度大于粉砂海床，可能是粉砂渗透性相对较好引起部分超孔隙水压力消散所致。双层海床与均质粉质黏土海床的累积孔隙水压力曲线几乎完全重合，分析可能是双层海床表面粉土层厚度仅有2 m，且粉土与粉质粘土的孔隙水压力发展模式及参数比较接近所致。

(10m水深均质粉土海床波浪作用60min。The case of homogeneous silty seabed with water depth of 10 m and wave duration of 60 min.)

图4 波浪条件对累积孔隙水压力的影响
Fig.4 Effects of wave conditions on residual pore pressure response

(10 m水深50年一遇波浪作用60 min均质海床响应。The case of homogeneous seabed with 10 m water depth and duration of 60min under 50-year once waves.)

图5 海床土层土性对累积孔隙水压力的影响
Fig.5 Effects of soil parameters on residual pore pressure response

图2～5的计算结果显示，不同波浪和海床组合下，最大超孔隙水压力约为40 kPa，其最大超孔隙水压力比u/σ0’约为0.8，即没有达到完全的液化。分析其原因：首先，相对于地震荷载，波浪荷载频率相对较低、强度相对较低，孔隙水压力累积速度相对较慢；波浪持续时间相对较长，以及海床表面自由排水的边界条件使得累积过程中部分孔隙水压力消散。其次，粉质土的孔隙水压力发展模式不同于砂土，粉质土中含有的少量黏粒成分限制了孔隙水压力的进一步累积升高，在尚未达到完全液化的情况下应变即已持续发展，这一点在土的不排水动力试验[9,20]和室内水槽试验[10]中均得到了验证。因此，波浪作用下粉质土海床不一定会出现超孔隙水压力比u/σ0’达到1的完全液化。按照有效应力原理，自由海床的累积孔隙水压力不可能超过有效应力，即超孔隙水压力比不能超过1，计算结果显示了本文模型的可靠性，避免了之前研究[2,8,13-16]中超孔隙水压力比超可能过1的错误情况。

值得注意的是，除完全液化之外，还存在冲刷和剪切破坏等海床失稳形式[1]。孔隙水压力的累积升高总会增大海床地基及结构物失稳破坏的几率，例如：累积孔隙水压力能够引起自下而上的渗流力，促进泥沙的起动和冲刷；累积孔隙水压力能够降低海床土的有效抗剪强度，进而诱发海底滑坡；累积孔隙水压力能够降低桩基承载力和管线的稳定性。本文给出的模型和算法简便、可靠，可为相应的海洋工程设计提供一定的参考和支持。

5 结论

(1)基于一维固结方程和双曲线型的孔隙水压力发展模式，采用有限差分方法并在MATAB编程求解，可简便、有效地实现波浪作用下粉质土海床的累积孔隙水压力响应分析。

(2)以黄河三角洲为背景的计算结果显示，粉质土海床中累积孔隙水压力随波浪持续时间的增加而增大，随波浪的剧烈程度增加而增大，在水深增大到8m时达到最大，均质粉土和粉质黏土海床中累积孔隙水压力大于粉砂海床，表面硬壳层的影响不明显。波浪引起的海床超孔隙水压力比在表层1m左右最大，但均未超过1，即可能发生除液化之外的其他形式的海床失稳。

[1] Sumer B M, Fredsøe J. The mechanics of scour in the marine environment [M]. Singapore: World Scientific, 2002.

[2] Jeng D S, Seymour B R, Li J. A new approximation for pore pressure accumulation in marine sediment due to water waves [J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2007, 31(1): 53-69.

[3] 许国辉, 王欣, 刘会欣, 等. 粉质土海岸微地貌形成及泥沙问题的工程地质分析 [J]. 海洋地质与第四纪地质, 2010, 30(2): 43-50.

[4] 冯秀丽, 林霖. 现代黄河水下三角洲全新世以来土层岩土工程参数与沉积环境之间的关系 [J]. 海岸工程, 1999, 18(4): 1-7.

[5] 周良勇, 刘健, 刘锡清, 等. 现代黄河三角洲滨浅海区的灾害地质 [J]. 海洋地质与第四纪地质, 2004, 24(3): 19-27.

[6] 李海东, 杨作升, 王厚杰, 等. 现代黄河水下三角洲地质灾害现象的空间分布 [J]. 海洋地质与第四纪地质, 2006, 26(4): 37-43.

[7] 杨少丽, 沈渭铨, 杨作升. 波浪作用下海底粉砂液化的机理分析 [J]. 岩土工程学报, 1995, 17(4): 28-37.

[8] 孙永福, 董立峰, 宋玉鹏. 黄河水下三角洲粉质土扰动土层特征及成因探析 [J]. 岩土力学, 2008, 29(6): 1494-1499.

[9] 曹成效, 刘乐军, 李培英, 等. 循环荷载作用下粉土的动力学特性 [J]. 海洋科学进展, 2007, 25(1): 54-62.

[10] Tzang S Y, Ou S H. Laboratory flume studies on monochromatic wave-fine sandy bed interactions: Part 1. Soil fluidization [J]. Coastal engineering, 2006, 53(11): 965-982.

[11] Sassa S, Takayama T, Mizutani M, et al. Field observations of the build-up and dissipation of residual pore water pressures in seabed sands under the passage of storm waves [J]. Journal of Coastal Research, 2006, 39: 410-414.

[12] 刘红军, 王虎, 张民生, 等. 波浪作用下黄河三角洲粉质土海床动力响应分析 [J]. 岩土力学, 2013, 34(7): 2065-2071.

[13] Seed H B, Rahman M S. Wave-induced pore pressure in relation to ocean floor stability of cohesionless soils [J]. Marine Georesources & Geotechnology, 1978, 3(2): 123-150.

[14] McDougal W G, Tsai Y T, Liu P L F, et al. Wave-induced pore water presure accumulation in marine soils [J]. Journal of Offshore Mechanics and Arctic Engineering, 1989 (111): 1-11.

[15] Cheng L, Sumer B M, Fredsøe J. Solutions of pore pressure build up due to progressive waves [J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2001, 25(9): 885-907.

[16] 栾茂田, 张晨明, 王栋, 等. 波浪作用下海床孔隙水压力发展过程与液化的数值分析 [J]. 水利学报, 2004, 2: 94-100.

[17] 潘冬子, 王立忠, 潘存鸿. 粉质海床波浪响应的数值模拟及试验研究 [J]. 岩土力学, 2008, 29(10): 2697-2707.

[18] 张建民, 谢定义. 饱和砂土振孔隙水压力增长的实用算法 [J]. 水利学报, 1991 (8): 45-51.

[19] 曾长女, 刘汉龙, 丰土根, 等. 饱和粉土孔隙水压力性状试验研究 [J]. 岩土力学, 2005, 26(12): 1963-1966.

[20] 刘红军, 王小花, 贾永刚, 等. 黄河三角洲饱和粉土液化特性及孔压模型试验研究 [J]. 岩土力学, 2005, 26(10): 83-87.

[21] 钱家欢, 殷宗泽. 土工原理与计算(第二版) [M]. 北京： 中国水利水电出版社, 1996: 200-201.

责任编辑 徐 环

A Simplified Analysis Method for Residual Pore Pressure Response of Silty Seabed Under Wave Loads

WANG Hu1, LIU Hong-Jun1,2

(1. The Key Laboratory of Marine Environment and Ecology, Ministry of Education; 2. College of Environmental Science and Engineering, Ocean University of China, Qingdao 266100, China)

The stability of seabed foundation is threatened by the wave-induced pore pressure, and residual pore pressure response is dominant for feebly cohesive fine-grained silty seabed under wave loads. For the widely distributed silty soil in coastal areas, the basic equations of wave-induced residual pore pressure in silty seabed is established based on the one-dimensional consolidation theory, in which a hyperbolic-shaped pore pressure development mode is particularly chosen as a source term. Finite differential scheme of the initial boundary value problem is derived and solved in MATLAB. The proposed model and corresponding algorithm are proved to be effective through the case study in the Yellow River delta, and can provide theoretic reference and technique support for the design of coastal and ocean engineering.

wave loads; silt; residual pore pressure; consolidation equation; finite difference; Yellow River delta

国家自然科学基金项目(41572247)；山东省科技发展计划项目(2014GGX104007)资助

2014-09-01；

2014-11-23

王 虎(1986-)，男，博士生。E-mail: wanghu824@126.com

TU431; TU392.5

A

1672-5174(2015)11-075-06

10.16441/j.cnki.hdxb.20140253