钛合金超塑成型/扩散连接舵面颤振设计

中 国 空 空 导 弹 研 究 院 张 鹏

洛阳奇瑞机械科技有限公司 赵 铮

中航工业北京航空制造工程研究所 廖金华

钛合金超塑成型/扩散连接工艺技术，是利用钛合金特定的显微组织，在适当的温度及压力下，其延伸率超过100%，甚至可达1000%的特性，进行超塑成型[1]和扩散连接。钛合金超塑成型/扩散连接结构具有重量轻、比强度和比刚度高及成型性好等特点，是解决导弹性能要求高、结构轻量化的有效途径。某型空空导弹舵面采用Ti-6AL-4V材料的超塑成型/扩散连接4层板结构，形成上下蒙皮加内部展向、弦向分布的加强筋结构，其静力强刚度通过调整4层钛板的厚度和加强筋的分布以满足设计要求。

飞行器在飞行中由于颤振造成失效或损坏是常见事故之一。颤振现象的本质是气动弹性运动不稳定现象，当升力面具有两个以上的自由度，在一定的临界速度（或动压）及相位关系下，可能发生耦合的等幅简谐振动。当速度超过临界值后，任一微小扰动均将引起发散性振动，严重时会使飞行器完全解体[2]。对于该型空空导弹，其飞行速度高，结构重量比和导弹刚度裕度小，舵面颤振设计是导弹能否满足全空域最大飞行动压要求的关键技术。

1 颤振分析原理

1.1 气动弹性运动方程

根据分析力学理论，完整多自由度保守系统的拉格朗日运动方程为[3]：

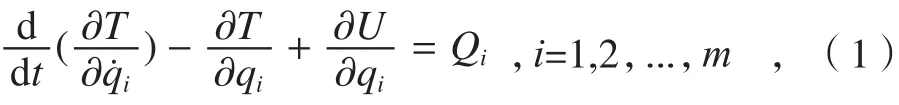
式中，T为系统的动能；U为系统的变形势能；Qi为对应第i阶模态的广义力；qi为第i阶广义坐标。

对于气动弹性系统，利用模态的正交性，其动能T可表示为：

同理，气动弹性系统的变形势能U可以表示为：

由广义力的定义，第i阶广义气动力Qi可以表示为

式中，fi为模态列阵，y=[y1y2...ym]T为气动力列阵。

当不计阻尼、忽略能量损耗时，气动弹性系统可认为是完整的保守系统。运用拉格朗日运动方程，将式（2）、（3）代入式（1）中，即得

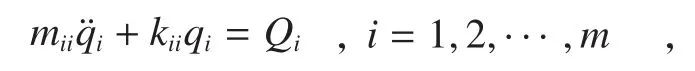
写成矩阵方程的形式为：

式中，q=[q1q2...qm]T为广义坐标列阵；M=diag[m11...，mmm] 为广义质量对角矩阵；K=diag[k11...，kmm]为广义刚度对角矩阵；Q为广义非定常气动力列阵，它也可表示成：

式中，ρ为气流密度；V为相对气流速度；A为广义非定常气动力影响系数矩阵。式（5）即为统一描述气动弹性问题的基本运动方程。

1.2 颤振方程的求解

颤振方程一般写为：

式中，广义非定常气动力矩阵A是关于马赫数与减缩频率 的复函数。颤振方程求解常用的有以下几种方法，如V-g法、p-k法等。由于p-k法可以反映一定的亚临界特性，目前工程上普遍采用p-k法进行颤振求解。

设机翼做任意运动（并不需要谐振荡运动），即设

式中，p=ω(γ+i)，这里γ为衰减率，结构阻尼g=2γ。

假设非定常气动力仍然是谐振荡的，将颤振方程改写为：

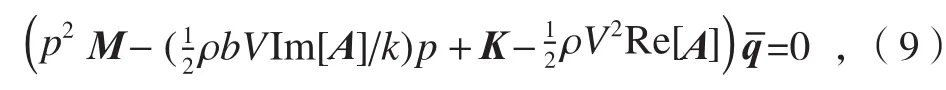
这里，减缩频率

容易推得， 即是实数矩阵[R]的特征值，其中

因而，颤振求解转化为关于实数矩阵R的特征值问题。当特征值为实数时，对应静气动弹性发散；当特征值为共轭复数对时，对应于动气弹颤振。

在具体的特征值求解过程中，由于矩阵R中的元素与减缩频率k有关，因而需要采用反复的迭代来求解。给定一系列的飞行速度Vi，对于每一个速度Vi，迭代求得m组收敛的g，ω，k值。于是，可以绘制出V-g图和V-ω图。从V-g图中可以确定g由负变正的临界点，即g=0时，相应的V为颤振速度，相应的ω为颤振频率。

MSC.Nastran是一种用于结构分析的大型有限元程序。其中的气弹分析模块MSC.FLD提供亚音速升力面理论（偶极子网格法）、超音速升力面理论（Zona51）、马赫数盒子法、活塞理论及片条理论等5种颤振分析的非定常气动力计算方法，可用于飞行器亚音速或超音速飞行的颤振计算。工程上常采用MSC.Nastran进行空空导弹的颤振分析与设计。

2 舵面颤振特性设计

2.1 舵型对颤振特性的影响

2.1.1 舵形选型及颤振模型的建立

空空导弹舵面外形常见的有三角形、梯形、蝶形和五边形等，如图1所示。对超声速、大攻角飞行的空空导弹，舵面多为大后掠角、小展弦比的气动外形。舵面外形设计中需考虑具有小的绞链力距、失速攻角大、良好的操纵性和颤振特性等要求，综合考虑该型空空导弹的系统要求，舵面外形初步选取碟形和五边形2种舵型。

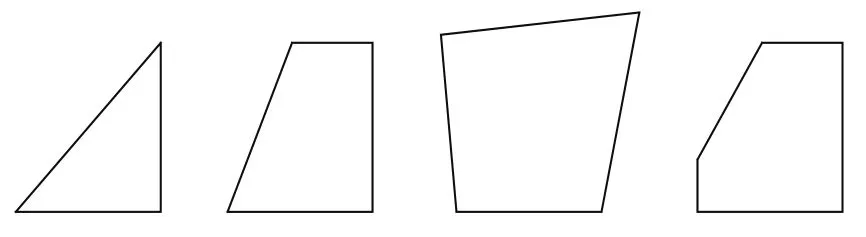
图1 舵面外形Fig.1 Outline of rudder

采用厚度6mm的铝合金碟形舵和五边形舵面进行颤振特性对比分析研究。舵面颤振模型中气动模型采用MSC. Nastran软件中气动CAERO1卡格式进行网格划分；结构模型由shell单元（三角形和矩形）和梁元构成，对舵面的支撑舵轴采用圆形截面梁元模拟。两种舵型结构网格如图2所示。

图2 五边形舵和碟形舵网格图Fig.2 Lattice of pentagonal and butterfly rudder

2.1.2 固支舵面颤振对比分析

对舵面的支撑梁元进行固支，采用3组不同的梁元截面惯性距进行舵面固有频率和颤振特性的分析，不同舵型的颤振特性对比如表1所示。

表1 不同舵型的颤振特性对比

2.1.3 同频率舵面颤振对比分析

根据初步方案舵面实测固有频率，选取舵面典型频率组合（见表2）,调整舵面的支撑梁元刚度，使2种舵型前两阶固有频率相同情况下进行颤振特性分析，同频率舵面的颤振特性对比如表2。

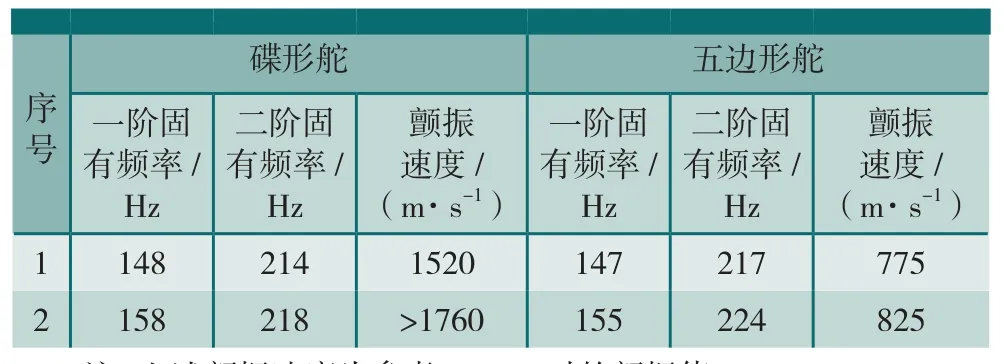
表2 同频率舵面颤振特性对比

分析结果表明：舵面平面形状对导弹颤振速度影响较大，碟形舵颤振特性明显优于五边形舵，综合导弹系统对舵面气动特性的要求，确定该型空空导弹选用碟形舵。

2.2 舵面重心设计

空空导弹主要有舵面颤振和舵面＋弹身组合体颤振两种模式。由于舵面＋弹身组合体颤振计算中包含舵面的颤振特性，一般采用舵面＋弹身组合体建模型式进行舵面及导弹的颤振分析，下文采用舵面＋弹身组合体颤振模型进行舵面重心设计。

2.2.1 颤振模型建立

（1）结构模型。

舵面＋弹身组合体采用半模进行有限元建模。按照弹身的实际壳体结构和分系统质量分布，采用CBAR梁元和质量节点元（CONM2单元）模拟弹身；其中梁元体现弹身的刚度特性，弹身的质量通过加在CBAR的节点上的质量元模拟；弹身节点对称自由度约束。弹身模型共有27个梁元素和28个质量节点元构成。舵翼面采用质量和刚度分布基本等效的shell单元构成。舵面＋弹身组合体模型如图3所示。

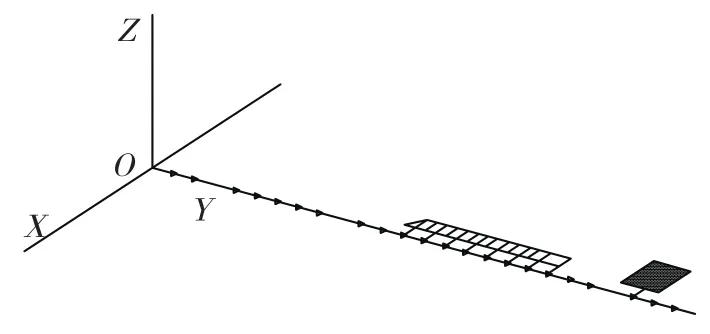
图3 舵面＋弹身组合体有限元模型Fig.3 FEM model of assembly of rudder surface and shell

（2）气动模型。

舵面＋弹身组合体气动模型采用半模进行网格划分，弹身采用气动CAERO1卡格式进行网格划分。亚音速气动力采用偶极子理论、超音速采用ZONA理论。弹身采用30个元素划分；翼面采用展向为3、弦向为25的网格划分，共75个元素；舵面分4区，共70个元素划分。气动网格如图4所示。

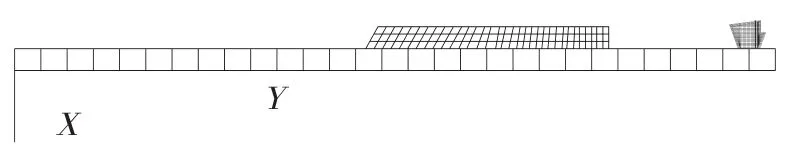
图4 舵面＋弹身组合体气动网格模型Fig.4 Lattice model of assembly of rudder surface and shell

2.2.2 不同舵面重心的颤振特性分析

根据初步方案舵面实测固有频率，选取两种舵面典型频率组合，对质心在舵轴前1～12mm状态舵面进行导弹颤振分析，分析结果如表3～4和图5～6。

上述分析数据表明，舵面质心在1～12mm变化范围内，在典型Ma数下颤振速度呈降低趋势，在舵面质心超过一定限度后颤振速度才迅速提高。

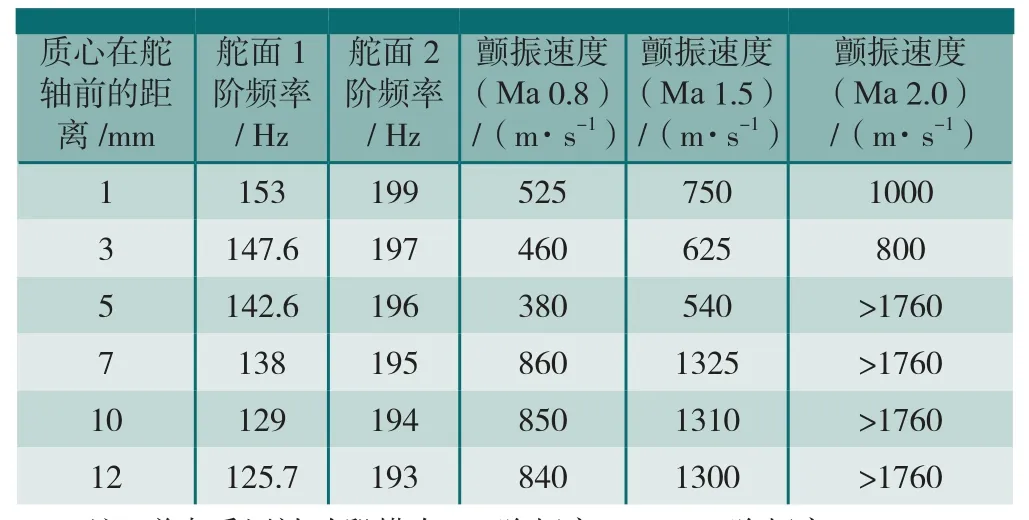
表3 不同质心舵面颤振特性1

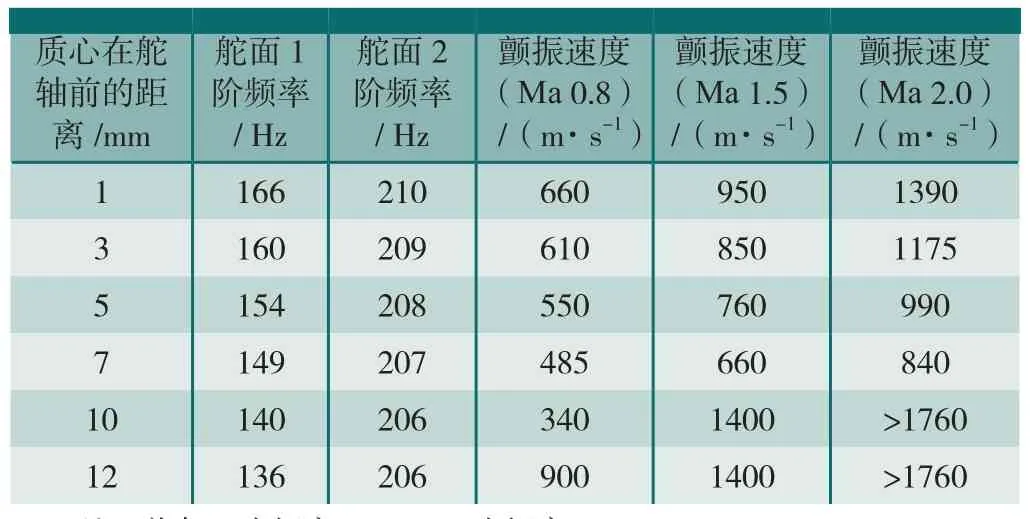
表4 不同质心舵面颤振特性2

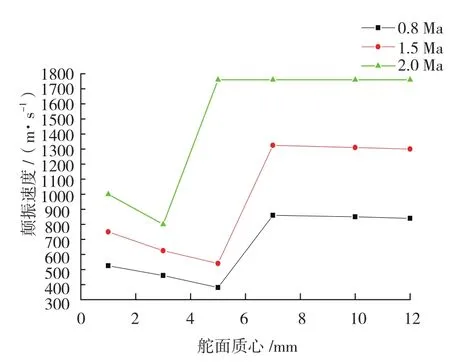
图5 质心位置-颤振速度曲线1Fig.5 Curve 1 of barycenter and flutter velocity

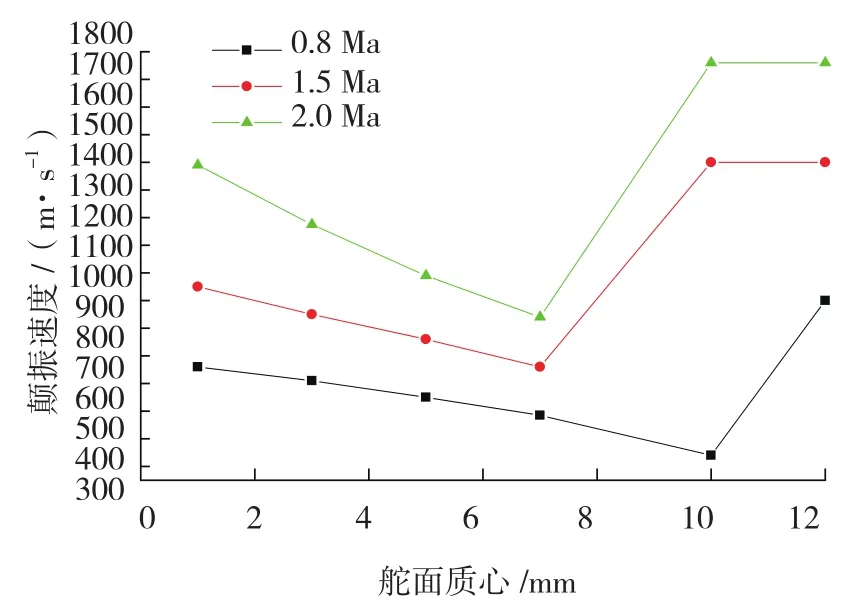
图6 质心位置-颤振速度曲线2Fig.6 Curve 2 of barycenter and flutter velocity

综合2.1、2.2节中分析和导弹系统对舵面重量等的要求，确定舵面采用碟形，舵面质心在舵轴前1～3mm。在此基础上，结合舵面静力强刚度分析，确定的超塑成型/扩散连接舵面结构为：钛合金4层结构，每层钛板厚度为0.55mm，前缘结构采用实心钛板结构，保证舵面的质心设计。舵面内部结构及强度分析如图7所示。

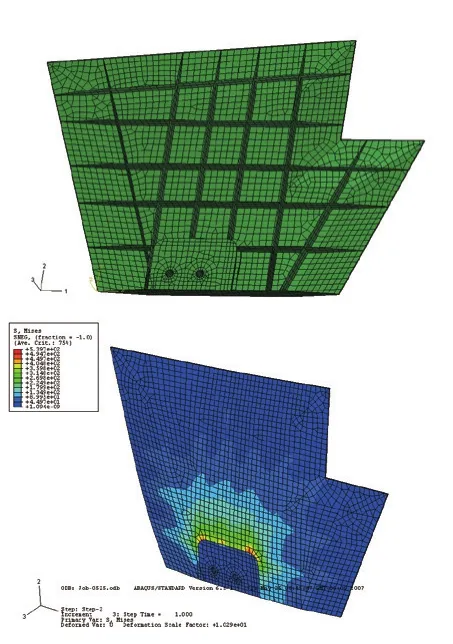
图7 舵面内部结构及强度分析结果Fig.7 Analysis of inner structure and strength of rudder surface

3 舵面颤振特性分析

3.1 颤振模型建立

舵面前缘为实心钛板结构，中后部采用外面2层钛板成型舵面的外蒙皮，其厚度为1.1mm，中部两层钛板形成沿展向、弦向的加强梁，提高舵面的整体刚度和蒙皮刚度。单片舵面质量500g，质心在舵轴前1～3mm。

整个舵面模型由shell单元（三角形和矩形）和梁元构成；对舵面舵接头、前缘区域和其他区域，采用shell单元划分，按照结构实际厚度或等效刚度进行属性定义，对于舵面中的沿展向和弦向的加强梁，采用矩形截面梁元模拟，全部模型共有1221个元素和1047个节点。全模质量：0.4952kg，舵面质心：舵轴前1mm。详细模型如图8所示。

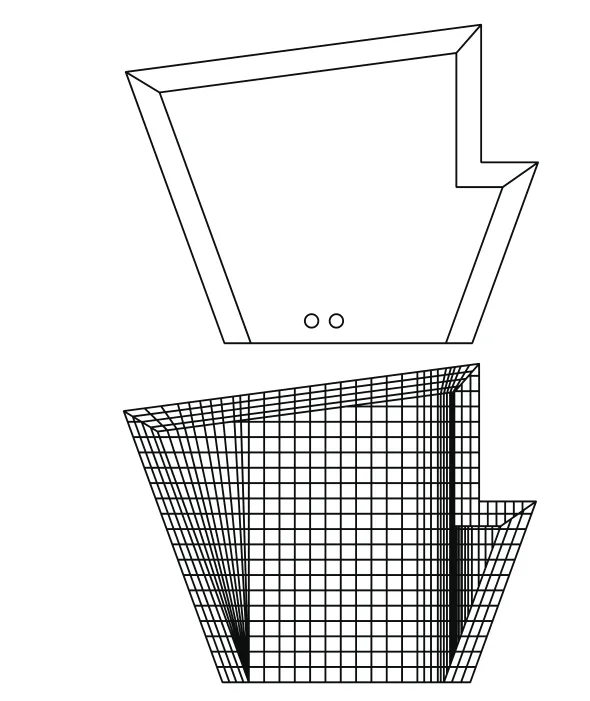
图8 舵面结构和有限元模型Fig.8 Structure and FEM model of rudder surface

舵面模型与2.2.1中弹身模型组合形成舵面＋弹身组合体结构模型，舵面＋弹身组合体气动网格同2.2.1节中气动模型。

3.2 舵面频率拉偏颤振组合分析

按确定的舵面结构方案进行产品试制和地面模态试验，舵面一阶频率在150～165Hz，二阶频率在200Hz以上，按此频率段进行适当的频率拉偏，采用迭代法进行颤振速度分析，分析结果见表5～6，表中频率单位为Hz，颤振速度单位为m/s。

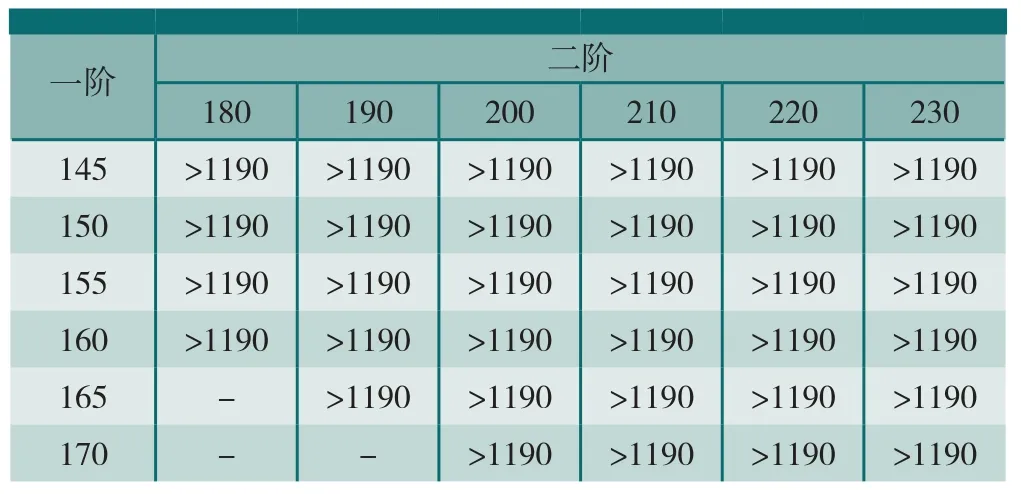
表5 舵面质心舵轴前1mm颤振分析

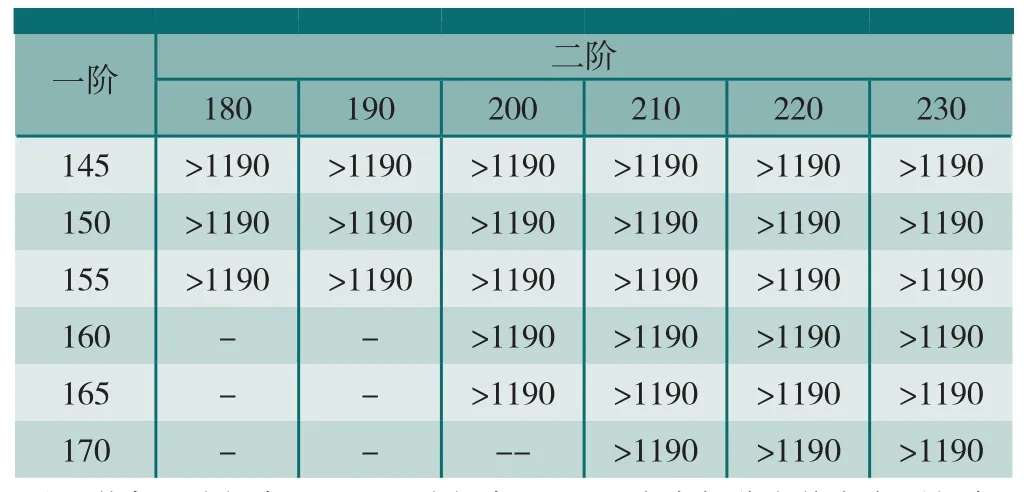
表6 舵面质心舵轴前3mm颤振分析

对舵面频率边界点进行不同马赫数下的颤振特性分析，分析结果见表7～8，表中频率单位为Hz，颤振速度单位为m/s。

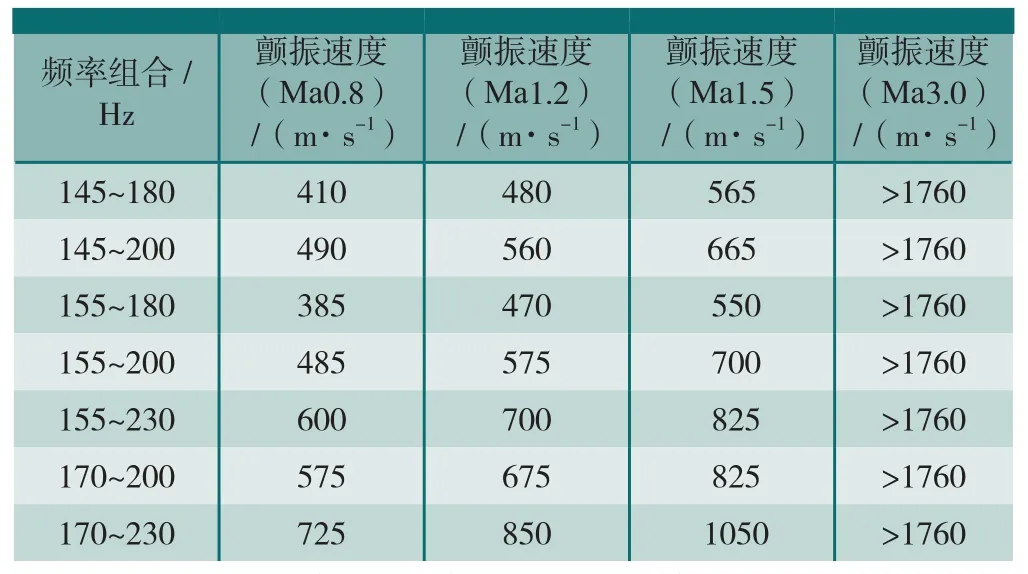
表7 舵面质心舵轴前1mm颤振分析

表8 舵面质心舵轴前1mm颤振分析

3.3 颤振裕度分析

经弹道计算分析，该型空空导弹20m高度发射条件下，导弹飞行动压为全空域最大动压：740179Pa。按照GJB1544-1992《战术导弹强度和刚度通用规范》中要求：导弹及其部件在全部设计规定的飞行高度和机动载荷条件下，在达到1.15VL（VL为极限速度）的全部速度范围内都不应发生颤振[4]，导弹颤振速度应至少有15%的裕度，0km高度颤振速度不低于1190m/s。

表5和表6中分析数据表明：导弹颤振速度均大于1190m/s。对舵面边界频率组合，在主动段和被动段进行了典型马赫数下颤振分析，各马赫数下颤振裕度都大于1.15，该型导弹颤振裕度满足设计要求。

4 结论

本文给出了钛合金超塑成型/扩散连接4层结构舵面颤振的设计方法。对某型空空导弹舵面外形及舵面重心对颤振特性的影响进行了对比分析，确定了满足全空域导弹颤振裕度的舵面结构。仿真表明：

（1）舵面平面形状对舵面颤振特性影响较大，舵面外形设计中，不仅要考虑具有好的气动特性，还需兼顾具有良好的颤振特性，外形上尽量选取形心在舵轴前的舵面平面形状。

（2）合理的舵面重心可提高导弹颤振速度，舵面重心布局应尽量在舵轴前，设计中舵面重心需综合导弹颤振特性和系统对舵面重量要求综合确定。

[1] 张鹏，廖金华.钛合金超塑成型/扩散连接弹翼结构设计.航空制造技术,2014(13):87-90.

[2] 吴小胜，黄晓鹏.一种弹翼颤振临界速度的快速计算方法.弹箭与制导学报,2004,24(3)：68-70.

[3] 杨超，吴志刚.飞行器气动弹性原理.北京：北京航空航天大学出版社，2011.

[4] 樊会涛，吕长起.空空导弹系统总体设计.北京：国防工业出版社，2007.