利用课堂提问实现数学教学三维目标

陈芝连

[摘要]三维目标是课堂教学所追求的，实现三维目标方法多种，利用课堂提问也能实现.

[关键词]三维目标课堂提问数学教学

[中图分类号]G633.6[文献标识码]A[文章编号]16746058（2015）020019

现代课程观认为，课程应当更为开放、复杂、丰富和多元；师生之间应有更多的互动与对话.因此，课堂提问作为师生互动与对话的一种重要方式，值得我们去认识和研究.目前数学课堂上虽然不缺提问，但仔细观察教师的课堂提问，发现往往是一些要求学生回答“是不是”“对不对”“会不会”等简单的判断型的问题，不能有效地利用提问促进学生思考、创新和培养学生的思维能力.也就是说，课堂提问作为一种数学教学的重要手段，还没能引起广大教师的注意.那么，如何利用课堂提问实现教学的三维目标？

一、利用课堂提问更好实现知识与技能目标

目前，教学仍受升学压力的影响，还把学生掌握知识与技能作为一节课的重要目标.为了突出掌握知识的重要性，教师往往夸夸其谈，复述和重复文本的内容、原理是什么、公式是如何推导出来的，例题是如何解的，等等；或者呈现的问题比较简单，局限于表层问题，一般是“这个问题弄懂了没有”“关于这个问题理解了吗”.这样的陈述或问题并没能引起学生的注意，更没有引起学生的积极思考和反应，致使学生掌握知识的效果大打折扣.为此，教师应充分研究与分析教材，提炼出关键性的问题，以引起学生的学习兴趣，启发学生思维，取得事半功倍的教学效果.

【案例1】在“函数的图像”的教学中，教师给学生自学课本的引例：利用函数方法表示正方形的面积S与边长的关系，接着教师逐个提出以下问题：（1）从刚才的学习中，可以了解表示函数的方法有哪些？（2）画函数图像要经过哪些步骤？（3）图像上的点是怎样得到的？（4）图像中的点（0，0）为什么是空心的？（5）为什么此函数的图像都在第一象限呢？（6）从图像中能否看出y与x有怎样的变化关系？这样的关系是否也可以从解析式或表格中看出？（7）你能确定点A（2，3）在这一函数图像上吗？有什么方法？点B（3，1），C（4，16）呢？

在这一教学过程中，学生通过对一个个问题的思考及与同桌或小组交流，理解和掌握了本节的知识目标：让学生了解绘制函数图像的具体过程，了解图像点的横纵坐标与自变量、函数值之间的对应关系，并掌握利用图像工具研究函数的方法.这样的学习，使学生掌握的知识更牢固，效果更好.

二、课堂提问落实过程与方法目标的有效方法

把“过程与方法”作为课程目标提出来，是课程改革的突出特点，体现了新课程“以学生为主体”的教学理念.新课程改革强调过程，强调学生探索新知的经历和获得新知的体验，要求教学过程中让学生“动”起来，主动地进行自主探究学习、合作探究学习，获得属于自己知识，形成自我学习的风格.只要教师精心设计提问，引导学生积极投入到问题的思考、讨论的气氛当中，引起学生之间、师生之间的激烈争论，使学生思维得到碰撞，实现学生主动参与，达成“过程与方法”目标.

教学过程中，教师往往用问题引领学生学习.但有时问题难度较大，或学生对初学的数学基本理论及其应用往往觉得难、解题时不会灵活应用.此时教师如果能灵活根据问题的特点，提出一些有梯度、有思维性、适应学生的特点的问题，就能使学生很好地参与到课堂学习中，并主动思考、主动探究问题.

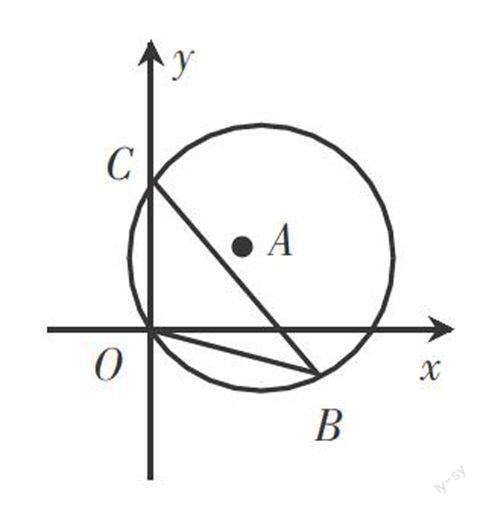
【案例2】在“三角函数”的教学中，教师给学生设计这样的一个问题：如右图，直径为10的⊙A经过点C（0，5）和O（0，0），B是y轴右侧⊙A劣弧上的一点，则sinB=.对于这个问题大多数学生无从下手，教师可提出以下问题：（1）sinB在什么环境中可求得？（2）∠B是哪个直角三角形的内角？（3）图中与∠B相等的角有哪些？（4）怎样能把∠B变为直角三角形的内角？请同学们小组讨论交流.这些问题由易到难，引导学生思考、应答.而且有了教师对问题的分解引导，学生的思考有了方向，特别是对提问（4）中的“变”非常感兴趣，自然地投入到小组探究中，表现出积极、主动的学习状态.最后教师提出一个反馈性问题：大家在解决这个问题时用到什么数学思想和解决问题的方法？让学生知道转化思想是一种常用的数学思想方法，而且通过大家共同合作能更好更快地找到解决问题的方法.

【案例3】在学习“勾股定理”时，教师给出这样的一个问题：在△ABC中，AB=15，AC=13，BC边上的高AD=12，求BC的长.学生基本上都是考虑△ABC是锐角三角形的情形，教师并没有直接说出另一个答案，而是逐步提问：你能说说如何算出这个结果吗？（学生画图说明），你画出的三角形是什么形状的？题目中有没有提到△ABC是锐角三角形？我们直接确定它是锐角三角形是否有些不妥？请同学们深思后，小组交流.

这一教学过程中，教师通过提问让学生展示自己的思维过程，能勇敢地表达自己的观点、方法，并且引导学生利用已有的数学知识、技能、数学思想方法去发现、分析问题，最终形成解决问题的方法.

【案例4】在“勾股定理的逆定理”的教学中，教师重视实验教学，培养学生数学能力

二、通过数学实验观察培养学生的形象思维能力

数学教学大纲将培养学生的三大能力之一的“逻辑思维能力”改为“思维能力”，虽然看上去只是去掉了两个字，但是这个概念的内涵却变得更加丰富有趣了，它可以促使我们在教学实践过程中能够进行认识上的大转变.人们认识事物的过程是从感性认识上升到理性认识，从抽象到具体.数学实验为学生的认识过程提供了大量具体而形象的素材，使学生更能生动形象地理解数学的抽象问题.

【案例2】“数学归纳法”的教学.

教师让学生预先准备一些形状相似的长方形木块，然后让学生按以下实验过程操作：

（1）竖起所有木块，让第一块倒下，发现余下的木块也全部倒下.

（2）把其中两块移开一些距离，让前面一块倒下时，碰不到下一块，然后让第一块倒下，发现还剩下一些木块没有倒下.

通过实验，让学生在探究中真正理解“全部倒下”的含义.接着教师与学生共同总结数学归纳法的定义.

（1）第一块必须倒下（递推基础）.

（2）第一块倒下，则第k+1块也倒下（递推关系）.

若每一个木块代表一个命题，则第一个命题成立，且有“第k个命题成立，则第k+1命题也成立”，则所有命题都成立.由此学生便能生动形象地掌握和应用数学归纳法.

数学实验能够创设形象思维的情境，为学生构建新的认识结构，提供直观形象的思维背景，引导学生进行思维，帮助学生形象地理解数学知识.因此，教学中教师应通过生动形象的数学实验引导学生理解抽象的数学知识.

三、利用数学实验培养学生的合情推理能力

课标指出，合情推理是能够根据已经有的正确的结论和事实、实践和实验的结果，以及个人的直觉和经验等推测某些结果的一些推理过程，类比、归纳是合情推理时最常用的思维方法.在解决问题的实际过程中，合情推理通常是具有猜测、发现、探索并能够提供思路的功能，有利于学生创新意识与能力的培养.

波利亚指出：“只要数学的学习过程稍能反映出数学发明的过程，那么就应让猜想合情合理地占有适当的位置.”因此，教师要根据具体的数学内容，合理地创设一些数学实验，引导学生通过动手实践、观察探索，进行合情推理的能力训练.

【案例3】已知a、b是已知方程u2+utanθ-1sinθ=0的两根，求证：不论θ为何值，过A（a，a2），B（b，b2）的直线恒切于一个定圆.

分析：过A、B的直线方程为：y=（a+b）x-ab，由韦达定理知a+b=-1tanθ，ab=-1sinθ，则y=-1tanθx+1sinθ，即ysinθ+xcosθ=1.

要证直线切于定圆，但因定圆未知，为此，不妨引导学生从实验开始.引导学生取θ=0，π2，π，32π分别得到直线x=1，y=1，x=-1，y=-1，让学生观察它们恰好围成一个正方形，从而不难猜测所找的定圆即圆心在原点的单位圆，从而找到解题思路.

对于许多无从下手的数学问题，教师若能创设一些合理的数学实验，提供解决问题的直观的思维背景，形成解决问题的途径，就能很好地培养学生合情推理的能力.

四、通过数学实验培养学生“用数学”的意识

数学课标明确指出：人人学有价值的数学，人人获得必需的数学，数学要为学生的生活服务.所以根据这一重要的教学思想，使得学生在自得知识的基础上，能够密切联系身边的生活实际问题，为学生创设更好、更开放的数学思维空间.在实施数学实验教学的过程中，学生学到的知识在实际应用中得到巩固，让学生“用数学”的意识得到很好的培养.

【案例4】遮阳棚如何搭建，才能使遮阳面积最大？

实验背景：夏日将至，农户都要搭阳棚，来种植蔬菜.遮阳棚如何搭建，才能使遮阳面积最大，这是农户最关心的问题.

教学过程：

（1）实验操作.有一个三角形遮阳棚△ABC，不妨设AC=3m，BC=4m，AB=5m，A、B是安置在地面上南北方向上的两定点，由正西上方的太阳射出的光线与地面成30°角，搭建遮阳棚.（如右图）

（2）观察猜想.学生移动遮阳棚△ABC（AB固定），在移动的过程中，如何使遮得的阴影△ABE的面积最大呢？猜测：当遮阳棚ABC与地面所成的二面角是60°时，遮得的阴影△ABE的面积最大.

（3）验证.（计算推理）使△ABE面积最大，由于AB定长，故只要AB边上的高最大即可.在△CFE中，利用余弦定理和三角函数的有界性，可得：当∠CFE与∠CEF互余时，EF最大，从而△ABE面积最大.

（4）拓展.在某时刻，当太阳光线与地面所成的线面角和遮阳棚与地面所成的二面角互余时，其遮得阴影部分面积最大.

学生通过综合运用立体几何知识解决了自己身边的实际问题，提高了学习兴趣，也使得“人人学有用的数学”的教育理念得到落实.

（责任编辑黄桂坚）