随机条件下部门资本预算独立方案的选择

耿春燕

摘要：在项目现金流量是确定的条件下，求解部门资本预算独立方案的选择方法有：0～1整数规划法、组合互斥化法和净现值率排序法，但在构成方案现金流量的数据具有不确定或随机性，即各期现金流量是随机变量时，如何选择部门资金预算的独立方案。文章讨论了在随机条件下如何运用期望值准则及其可能性，并给出了数值案例演示了利用软件在随机条件下三种选择方法一般求解过程。

关键词：随机变量；净现值；期望值；最优组合方案

一、引言

部门资本预算，不仅涉及多个投资项目，而且涉及资金的数量，即在资金有限条件下投资项目如何优选的问题。在资金有限的条件下，如何选择最合理、最有利的投资方向和投资项目，使有限的资金获得更大的经济效益，这就是企业进行资本预算时所面临的资金分配问题。

在确定条件下，有资金约束条件下的独立方案选择，其根本原则在于使用有限的资金获得最大的经济效益，即组合方案的净现值之和最大，实质上是个0～1整数规划问题，其目标函数可以写作：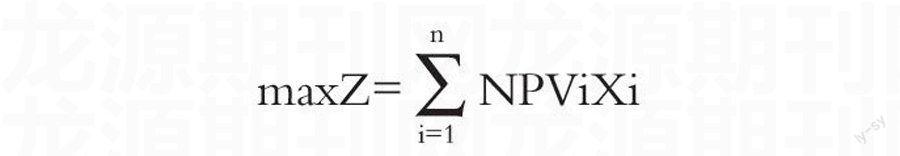

maxZ=NPViXi

式中NPVi——第 i个投资项目的净现值；

Xi——决策变量。其取值为1或 0。Xi取值为 1，表示第i个投资项目被接受；Xi取值为 0，表示第 i个投资项目被舍弃。i= 1， 2，…，n 。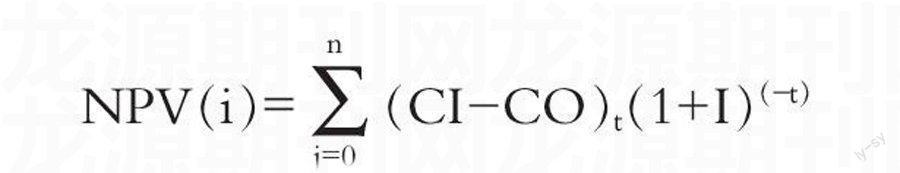

资源约束：

IiXi≤I

整数规划法适用于当方案数（n）较多时，利用整数规划的常用软件（如LINDO或WinQSB）或EXCEL中自带的规划工具就可以快捷和方便地求解，且能在各种情况下均能保证获得最佳的组合方案。

互斥组合法就是在资金限量条件下，选择一组不突破资金限额而经济效益又最大的互斥组合投资项目作为分配资金的对象。当存在多个投资项目时，不论其相互关系如何，都可以把它们组成许多互斥组合，并按净现值、年值等指标计算各互斥组合的经济效益，在不突破资金限额的条件下，选取经济效益最大的一组投资项目作为分配资金的对象。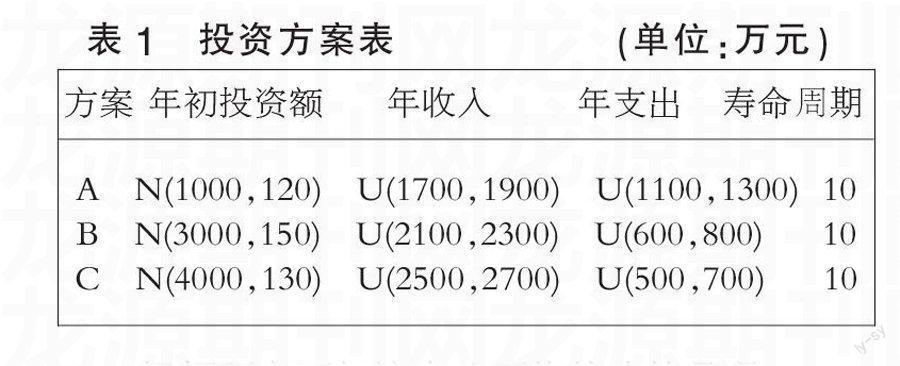

其评价的基本步骤如下。

第一，分别对各独立方案进行绝对效果检验。即剔除NPV<0的方案。

第二，对通过绝对效果检验的方案，列出不超过总投资限额的所有组合投资方案，则这些组合方案之间具有互斥的关系。

第三，将各组合方案按初始投资额大小顺序排序，按互斥方案的比选原则，选择最优的方案组合，即分别计算各组合方案的净现值，以净现值最大的组合方案为最佳方案组合。

在有资金预算的条件下运用组合方案互斥法进行比选，其优点在于能保证获得最佳的组合方案，但当方案数目较大时，于方案组合数（2n）较大，用组合互斥法虽然可行但是工作量较大，所以计算起来很繁琐且容易错误。

净现值率法是一种在计划期资金限额内先选择净现值率大的投资项目，直到资金限额分完为止的项目选择方法。其具体做法是把能满足最低期望盈利率的投资项目，按净现值率由大至小顺序排列，首先将资金分配给净现值率最大的项目，直到全部资金分完为止。

净现值率法的优点在于应用简单，一般能求得投资经济效率较大的项目组合，但不一定能取得最优的项目组合。

以上的评价方法都是针对在确定条件下（各期现金流量为常数）的经济评价。和确定条件下的经济评价一样，随机条件下的经济评价也主要面临如何运用三种方法的进行评价问题。本文将探讨随机条件下，在期望决策准则下用上述方法选择有资金预算的独立方案。

二、随机条件下的期望值准则及期望值

这里假设各方案的折现率为确定常数，在确定情况下方案净现值的计算表达式为：

NPV（i）=（CI-CO）t（1+I）（-t）

CI 表示现金流入，CO表示现金流出，I表示折现率。

在随机条件下各方案的现金流量是随机变量，即CI 、CO是随机变量，根据期望值准则取其期望值，就可以计算出每期确定的净现金流量。进而可以得到各方案的净现值期望值，便成为了确定条件下的情况了，就可以用三种方法来进行求解了。于是计算表达式就变为：

E（NPV（i））=（E（CI）-E（CO））t（1+I）（-t）

CI -现金流入，CO-表示现金流出，I-折现率

问题在于如何获得期望值。关于这些值的一般计算方法在概率论和数理统计类教材和文献中均有详细介绍，在方案经济评价中，确定期望值的主要途径有两种：一是利用中心极限定理確定。根据中心极限定理，当方案的现金流量足够多时，方案的评价指标近似服从正态分布。因此，在此理论下，由于评价指标的分布已知，问题的关键在于确定出分布的期望值和方差值，当期望值和方差值已知，就可以利用正态分布标准化等技术计算概率值。二是利用随机模拟确定。对于随机条件下的问题基本上都可以采用随机模拟求解期望、方差和发生概率。

三、案例计算

设某企业未来资金额是一随机变量，且服从正态分布，N（4500，100）。现有A、B、C三个独立方案，寿命期均为10年，且三个方案均满足各方案的初始投资、年收益和年支出也均为随机变量，具体如表1所示。公司要求的最低收益率为8%，该企业会选择哪些方案？

根据题意可知该企业面临的决策是现金流不确定条件下的有资金预算的独立方案选择问题。现金流量为一随机变量，分布为正态或均匀分布，即年收入（CI） 、年支出（CO）是随机变量，根据期望值准则取其期望值，就可以计算出每期确定的净现金流量。进而可以得到各方案的净现值期望值，便成为了确定条件下的情况了，就可以用三种方法来进行求解了。

确定各方案的净现值期望值：

E（NPVA）=-1000+（1700+1900）/2 （P/A，8%，10）-（1100+1300）/2 （P/A，8%，10）=3026.06

E（NPVB）=-3000+（2100+2300）/2 （P/A，8%，10）-（600+800）/2 （P/A，8%，10）=7065.15

E（NPVC）=-4000+（2500+2700）/2 （P/A，8%，10）-（500+700）/2 （P/A，8%，10）=9420.2

上式中（P/A，8%，10）是年金现值系数，查表可知为6.7101。可知三个方案的净现值期望值均大于零，三个方案都通过了“绝对效果检验”。

各方案投资期望值依次为：E（IA）=1000，E（IB）=3000，E（IC）=4000

1. 0～1整数规划求解（利用EXCEL软件）

在不确定情况下整数规划的目标函数应该改写为：

maxZ=E（NPVi）xi

式中NPVi——第 i个投资项目的净现值；

Xi——决策变量。其取值为1或 0。Xi取值为 1，表示第i个投资项目被接受；Xi取值为 0，表示第 i个投资项目被舍弃。i= 1， 2，…，n。

资源约束：

E（Ii）xi≤E（I）

根据以上计算结果和函数，获得该问题的0-1整数规划模型

MAX（3026.06x1+7065.15x2+9420.20x3）

s.t 1000x1+3000x2+4000x3≤4500

x1，x2 ，x3=0或1

根据以上模型，利用EXCEL自带的整数规划工具或LINDO软件可获得结果，这里为方便使用了EXCEL中工具栏的整数规划求解，选择A和B，最大期望净现值为10091.21，输入过程和计算结果如图1所示。

2. 互斥组合法

3个独立方案可以有23 个互斥组合方案，如表2所。

从以表2中可知AC BC ABC 期望投资总额均超过期望的资本预算，舍去，故最优的方案组合为AB ，期望的最大净现值为10091.21，与0-1整数规划化解出结果的一致。

3. 净现值率法

从表3可知，最佳方案组合投资为：A+B=4000（万元）。最佳方案组合净现值为：A+B=10091.21。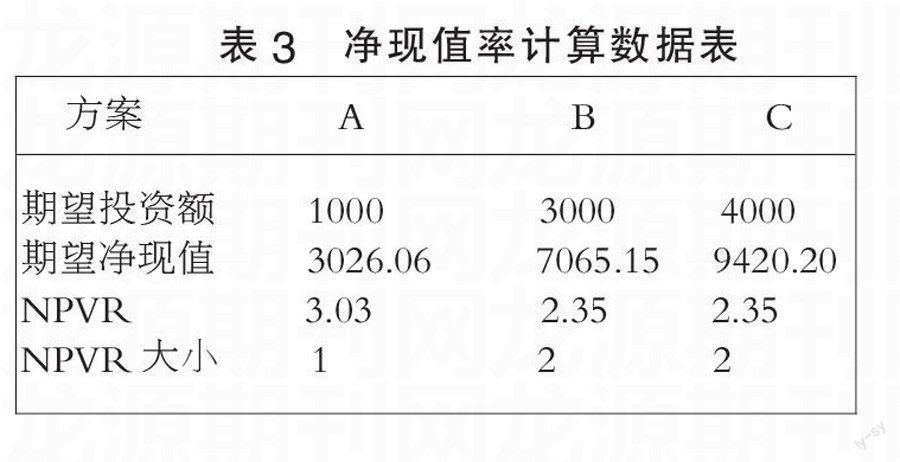

与前面二种方法结论一致。值得注意的是净现值率法应用简单，一般能求得投资经济效率較大的项目组合，但不一定能取得最优的项目组合。在有明显的资金总额量限制，且各项目资金远小于资金总拥有量时，适宜用净现值率进行方案选优。

四、结论

本文讨论了在企业有资本预算，项目的现金流量是随机变量条件下，用三种选择方法0～1整数规划法、组合互斥化法和净现值率排序法的求解问题。利用中心极限定理或随机模拟方法确定了方案的各期现金流量的分布和期望值，进而可以计算出各方案的净现值期望值和投资期望值后。这些问题成为了确定条件下的情况了，就可以用三种方法来进行求解了。给出了实例，利用软件求解了三种方法的一般过程，但本文未涉及如何利用中心极限定理或随机模拟方法确定了方案的各期现金流量的分布和期望值，这是个需要认真研究的问题。

参考文献：

[1]刘晓君，等.工程经济学[M].北京：中国建筑工业出版社，2006.

[2]向寿生.Excel在投资项目概率分析中的应用[J].商业研究，2008（07）.

[3]李国平.刘成，基于0-1规划的EXCEL整数规划求解[J].科教文汇，2009（06）.

[4]邵颖红.工程经济学[M].上海：同济大学出版社，2009.

（作者单位：重庆建筑工程职业学院）