浅谈数学课堂中的问题设计

廖石平

将教学目标问题化，让问题引领课堂教学已经成为一种常态化教学模式.然而，在实际操作过程中，经常出现问题设置无效等不合理现象.那么怎样才能提出问题引导学生主动参与，使我们的数学教学问得出彩有效呢？下面结合教学实际笔者谈谈的一些做法与认识.

一、问题设计应落在“最近发展区”，突出学生的主体地位

学生是课堂中的主体，问题的设计应该从学生的认知水平出发，以学定“问”，立足于学生的“最近发展区”，由浅入深、由感性到理性地设计问题.这样才能引导和帮助学生思考问题、分析问题和解决问题.

案例1 梯形的中位线性质

如图，在梯形ABCD中，AD∥BC，AE=BE，DF=CF，求证：EF∥BC，EF=12（AD+BC）.

此题的证明对大多数学生是有难度的，教师应该设计以下一组问题：

（1）这个题目的结论部分与哪个定理比较接近？（三角形中位线定理）

（2）能把EF转化为某个三角形的中位线吗？

（3）已知E是AB的中点，能否使点F成为以A为端点的某条线段的中点呢？应该怎样添加辅助线？

（4）能否证明EF为ABG的中位线？关键在于证明什么？（F为AG的中点）

（5）怎样证明AF=AG？

说明 该案例中的提问从学生的认知水平出发，设置的问题是从“已知区”逐步靠近“未知区”，促使学生积极主动探求新知，使新旧知识发生相互作用，产生有机联系.

二、问题设计应体现学法指导，促进学生反思学习

反思可以沟通新旧知识的联系，促进知识的同化和迁移；可以拓宽思路，优化解法，完善思维过程.

案例2 勾股定理

在学生学习勾股定理一课时，教师设计如下课堂小结问题：

（1）是不是所有的三角形三边都满足勾股定理？

（2）在发现勾股定理过程中，我们用了什么方法？

（3）据不完全统计，勾股定理的证明方法已经多达400多种，今天我们用了什么方法？

（4）运用勾股定理应注意哪些事项？

说明 这组问题概括了本节课的核心知识，强调了重点，指明了关键.问题（2）通过梳理知识和探究方法，给学生留下一个清晰的整体印象，帮助他们理解、掌握知识和技能以及数学思想和方法，真正获得数学活动的经验.问题（3）激发了孩子们的探求欲望和兴趣.整个问题设计使学生学会了总结数学课堂学习活动，培养学生的自我反思能力.

三、问题设计应落实探究的理念，实现学习方式的转变

依据新课程标准，教师通过设置若干组问题，由表及里，层层推进，引导学生探求问题的实质，把握问题的核心，拓展延伸，为培养学生的创新能力、实践能力搭好台阶.

案例3 探究中点四边形

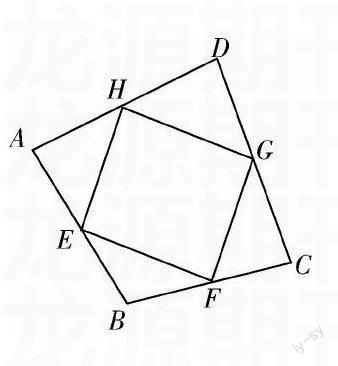
如图，在四边形ABCD中，E，F，G，H分别是AB，BC，CD，DA四边的中点，连接EFGH.求证：四边形EFGH是平行四边形.

这个问题的证明并不难，但教学不能到此为止，教师可以设计如下问题引导学生进一步探究该系列问题的本质.

（1）分别顺次连接以下四边形的四条边的中点，所得到的是什么四边形？

①平行四边形 ②矩形 ③菱形 ④正方形 ⑤梯形 ⑥直角梯形 ⑦等腰梯形

（2）決定这些中点四边形的因素是什么？从中你能发现什么规律？

（3）顺次连接n（n≥4）边形各边的中点，能得到怎样的n边形？顺次连接正n边形各边的中点，得到的是怎样的n边形？它们是正多边形吗？

（4）从上述问题的解决过程中，你受到哪些启示？

说明 通过问题（1）的探索，激发学生的探索热情，问题（2）的解决让学生体会到这一问题的本质所在（对角线的条件决定中点四边形类型），问题（3）从特殊走向一般，是培养数学能力的重要一步，问题（4）有助于让学生深入理解知识，体会数学思想及研究方法.

四、问题设计应基于对数学的理解，有效达成教学目标

新课程改革的一个显著特点就是把握数学的本质，理解数学，提高素养.一节数学课，有什么核心概念？涉及哪些数学思想方法？要解决哪几个主要问题？怎样去发现？每一个问题的解决需要铺设哪些“台阶”？学生可能会遇到哪些问题？这些都是教师必须在教学设计中要给予充分考虑的.教师在课堂教学中，要以问题为主线，启迪学生思考，使学生在课堂学习中深刻地感受如何发现问题、提出问题、分析问题、解决问题的整个过程，理解和认识知识发生和发展的必然的因果关系，从中领悟分析、思考和解决问题的思想方法.

如果把学生的大脑比作一泓平静的池水，那么教师在课堂设置的一个个问题就犹如投入池中的一块块石子，问题可以激起学生思维的涟漪和心灵的浪花.好的问题能搭起学生知识与能力的桥梁，大大提升学生的思维品质，提高我们的课堂教学效率.