RMI原则下高中解析几何解题教学探究

冯兴进　卢建川

一、解析几何产生的历史背景

众所周知，解析几何是代数和几何相结合的产物.比笛卡尔早出生56年的韦达，在前人的经验的基础上，有意识地系统地使用字母表示数，在他的成名作《分析入门》一书里，把代数看作一门符号化的科学，也正因为这一贡献，韦达被西方称为“代数之父”.代数的成熟，为笛卡尔向解析几何的迈进奠定了基础.出生在1596年3月31日的笛卡尔，他是一个十分注重方法的大家，他在自己创立的哲学中证明上帝的存在，并认为上帝一定是按照数学定律来建立自然界的.所以笛卡尔认为作为来源于自然界的形式几何也应是数学的化身（当时数学指的大多是代数）.而事实上，笛卡尔在这方面做的更多的是把代数用到几何上去.笛卡尔所创立的解析几何的精髓在于他不仅把前人的网格简化为坐标系（笛卡尔的坐标系与今天的平面直角坐标系不同，他不要求横轴和另一坐标轴的夹角互相垂直），并且把字母表示数引入到几何学中去.有了笛卡尔所迈出的具有决定意义的第一步，人类对几何的研究从“定性”推进到“定量”了.值得注意的是：笛卡尔是从几何出发然后寻找到几何的方程.而与笛卡尔恰恰相反，出生于1601年的费马却是从代数方程出发画出方程所表示的几何，就像用描点法作图一样.

从解析几何产生的历史背景我们可以知道：解析几何不仅使得几何与数量、运动与静止、辩证与算术开始融为一体，它还是数学走向空间解析几何的一个启示，是微积分产生的历史条件.所以解析几何的教育价值是非凡的.解题是我们当前数学教育的一大任务，所以在具体的解析几何解题教学中我们要体现它原有的综合性和融合性，展现数学的统一.

二、高中解析几何解题教学的性质和现状

解析几何的产生是得益于几何和代数的成熟发展，就解析几何解题本身而言，就如弗莱登塔

尔所言，解析几何就是一些算法.现行的高中解析几何知识教学中，大多数学教师认为解析几何的学科性质是偏重于代数的，学生学习解析几何的宗旨就是要学会代数计算和代数方法；课程目标就是让学生学会列方程，熟练解方程，即使注重数形结合这一核心思想，也侧重于几何问题代数化这单一的方面；教学上偏重于列方程和解方程，以训练算法为主，靠做大量习题提高代数技巧.在具体问题的解决过程中还会涉及用到许多的思想方法，例如：映射、化归、方程、函数、分类、变换、参数等.然而高中解析几何题要解题者得到的结论形式要么是代数关系要么是几何结论.那我们如何运用头脑中已有的由代数和几何综合而成的解析几何知识得到这般的结论呢？如果在此过程中还涉及其他思想方法，这些思想方法能否实现为解题者“雪中送炭”呢？这一切取决于解题者有没有一定的实践指导原则.

三、高中解析几何解题教学探究——基于RMI原则

由于解析几何是几何和代数的混沌，作为解题者如何把握好这种混沌的知识，让它们更好地引领我们得到我们想要的代数关系或者几何结论呢？

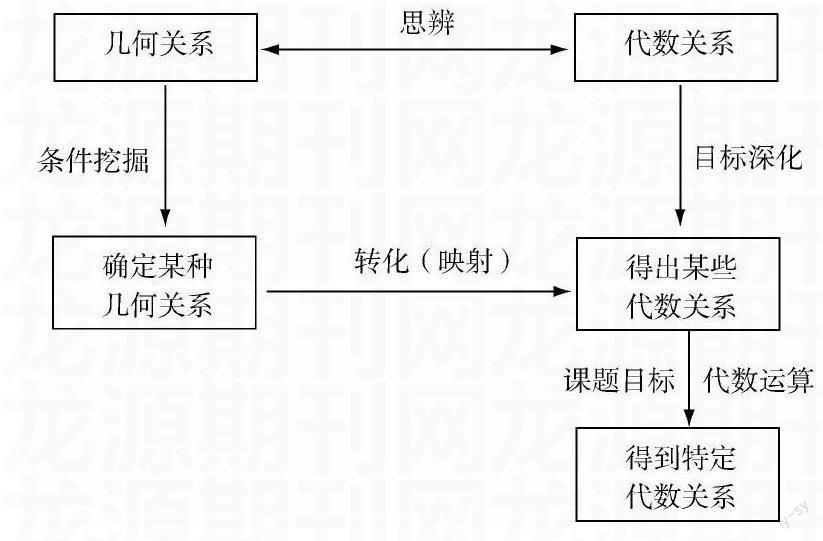
从解析几何产生的历史背景我们可以知道：解析几何其实就是代数、几何与笛卡尔坐标平面共同构成的一个映射，它们之间的互相转化就是映射和反演两种操作的完成.通常，一个几何问题无非是关于某些特定几何图像间的关系问题.这种关系结构问题在笛卡尔坐标平面的映射下便转化为代数式之间的关系问题.于是通过代数运算不难求得所需的一些代数关系.这些关系再翻译回去就可得出原来几何图形间的某种几何结论.上述就是解答解析几何问题的思想方法，可以简单地用框图表示：

综上，解答解析几何问题的基本思想是符合RMI原则的.在解析几何解题教学中以RMI原则为指导，不但可以在方法上更好地让我们运用混沌的解析几何知识得到单纯的代数关系或几何结论；而且可以客观上影响目前高中解析几何解题教学的导向，从而促进解析几何课程科学有效地实施.在具体解题教学中，我们如何体现RMI原则呢？

[2013年广东理数A卷20题]已知抛物线C的顶点为原点，其焦点F（0，c）（c>0）到直线l：x-y-2=0的距离为32[]2.设P为直线l上的点，过点P作抛物线C的两条切线PA，PB，其中A，B为切点.

（Ⅰ） 求抛物线C的方程；

（Ⅱ） 当点P（x0，y0）为直线l上的定点时，求直线AB的方程；

（Ⅲ） 当点P在直线l上移动时，求|AF|·|BF|的最小值.

分析 显然这道题要求我们得到的结论都是代数关系的形式，所以把题中的几何图像及其之间的位置关系转化为代数式及其之间的代数关系是该道题的主要方向，通过对代数关系进行一定的代数运算得到特定的代数关系是解题的主要任务.

（Ⅰ） 依题意，设抛物线C的方程为x2=4cy，由|0-c-2|[]2=32[]2结合c>0，

解得c=1.所以抛物线C的方程为x2=4y.

（Ⅱ） 抛物线C的方程为x2=4y，即y=1[]4x2，求导得y′=1[]2x.

设A（x1，y1），B（x2，y2）其中y1=x21[]4，y2=x22[]4，则切线PA，PB的斜率分别为1[]2x1，1[]2x2，

所以切线PA的方程为y-y1=x1[]2（x-x1），即y=x1[]2x-x21[]2+y1，即x1x-2y-2y1=0.

同理可得切线PB的方程为x2x-2y-2y2=0.

因为切线PA，PB均过点P（x0，y0），所以x1x0-2y0-2y1=0，x2x0-2y0-2y2=0.

所以（x1，y1），（x2，y2）为方程x0x-2y0-2y=0的两组解.

所以直线AB的方程为x0x-2y-2y0=0.

（Ⅲ） 由抛物线定义可知|AF|=y1+1，|BF|=y2+1，

所以|AF|·|BF|=（y1+1）（y2+1）=y1y2+（y1+y2）+1.

联立方程x0x-2y-2y0=0

x2=4y

，消去x整理得y2+（2y0-x20）y+y20=0.

由一元二次方程根与系数的关系可得y1+y2=x20-2y0，y1y2=y20.

所以|AF|·|BF|=y1y2+（y1+y2）+1=y20+x20-2y0+1.

又点P（x0，y0）在直线l上，所以x0=y0+2.

所以y20+x20-2y0+1=2y20+2y0+5=2y0+1[]22+9[]2.

所以当y0=-1[]2时，|AF|·|BF|取得最小值，且最小值为9[]2.

点评 （1）该题的第一问显然简单，但我们要知道它为什么如此简单.这是由于我们需要转化的几何和几何关系本来就少，而且转化之后得到的代数关系是简单的一元一次方程，固然第一问即是一元一次方程的求解问题.

（2）第二問需要转化的几何和几何关系是：两条切线和交点P与切线的关系.对应转化得到两切线的方程，P点坐标同时满足两切线方程.所以第二问的关键在于由代数关系观察抽象得到直线AB的方程.

（3）第三问需要转化的几何是：问题中的|AF|·|BF|和P与直线l的关系.对应转化得到（y1+1）（y2+1）=y1y2+（y1+y2）+1（二元二次函数）和x0=y0+2.此时可以发现问题的解决就是如何通过已有的代数式把二元二次函数消元变成一元二次函数，以便把最值问题转化为求一元二次函数的最值问题.

所以该题的整个解题过程基本可以归纳为这样一个框架：

四、结 语

以RMI原则指导实践解析几何解题教学是解析几何课程教学本质的需要，能很好地实现教师教学的宗旨和充分体现解析几何的教育价值.在实际课堂中，基于RMI原则的解析几何解题教学还可以促进师生课堂的共同探究和交流，培养学生的思辨能力.弗莱登塔尔认为任何思辨的新生事物都在其自身中包含着算法的萌芽，这是数学的特点.算法化意味着巩固，为更深的发掘提供技巧，我们在解析几何解题中仅仅体现解析几何算法的本质是不够的，更要体现解析几何在思辨之后对算法的更高需求的这种跳跃，这不仅仅是数学的特点，更是数学的魅力.