利用错题资源提高学生的空间思维能力

褚方群

上好错题分析课可提高学生的解题能力，改错是引导学生辨析正误的重要手段，是对数学概念本质和数学思想方法理解的加深。因此，教师一定要平和、理智地看待，并辅之以策略处理，充分利用错误再生资源，让“错误”美丽起来，从而提高学生的空间思维能力。我是从以下几方面着手的：

一、利用错题资源直观画图，提高学生的空间思维能力

结合直观认识，学会作图、识图。先从最简单的图形（如直线和平面）和最简单的几何体（如：正方体）开始画起，循序渐进地画出常用的几何体的直观图，直至能熟练的利用几何体的直观图还原出几何体的真实形状。例如碰到这样的练习题：一根长12米的方木，锯成相等的3段，表面积比原来增加了120平方分米，这根方木的体积是多少立方分米？有一小部分学生经常做成这样的错题：120÷6=20（平方分米）20×12=240（立方分米）。做成这样的学生有两个错点，一是不知道锯成相等的3段只增加4个侧面积，二是没有注意单位。这时我就引导学生画图，画出简单的直观图，让学生真正体会锯成相等的3段只增加4个侧面积，那这道题的难点就突破了，也就迎刃而解了。这样长期培养学生的作图能力，就能提高学生的空间思维能力，解题能力就能起到事半功倍的效果。

二、利用错题资源重视公式，提高学生的空间思维能力

高度重视概念，公式.不但要求学生内容准确记忆，但关键是一定要理解公式，知道公式的由来。学生在学习和完成作业的过程中，只是采用了死板的、公式化的方法求解题目，而没有真正意义上的理解空间图形的解题方法，学生的思维仅停留在表面上。这说明在我们的教学中必须要高度重视对概念、公式的由来，对学生进行足够的空间思维能力的培养。例如在试卷里考到这样一道题：一个长180厘米，宽45厘米，高18厘米的长方体木料，锯成了尽可能大的正方体木块（不余料）。这些小正方体木块的棱长最大可以是多少厘米？共锯成多少块？从考试情况看，第一个问题的解答正确率比较高，但第二个问题的解答正确率就比较低，有一部分学生错做成了：180÷9+45÷9+18÷9=27（块），这个错误的原因就是学生没有真正理解长方体、正方体体积公式的含义，学生没有真正理解长方体上锯成这样的立方体是怎样排列的。所以我让学生重新回忆长方体、正方体体积公式的由来，再观察长方体上锯成这样的立方体的直观图，做错的学生马上明白第二个问题的正确解答方法：（180÷9）×（45÷9）×（18÷9）=200（块）

三、利用错题资源学会“迁移”，提高学生的空间思维能力

让学生学会“迁移”，在迁移中提高逻辑思维能力，提高学生的空间思维能力。迁移思想是一个极其重要的数学思想，在立体几何中这一思想显得尤为重要，它是学好本单元的关键所在。倘若教师在教学中，经常能渗透“迁移思想”，学生的“迁移”能力必将得到提高，从而使他们在不知不觉中提高逻辑思维能力，提高学生的空间思维能力。

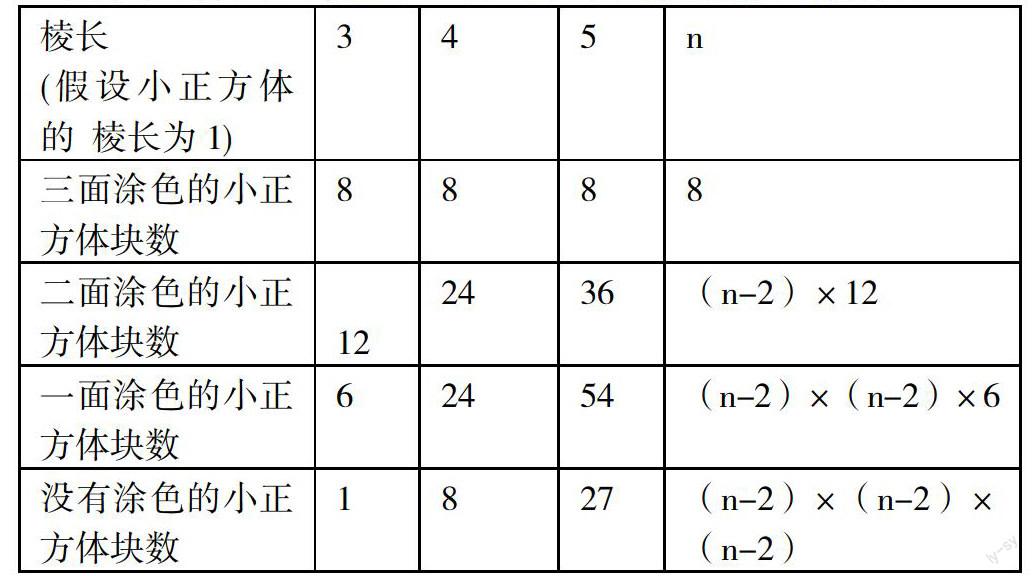
例如练习中有这样一道拓展题：一个长方体木块长5分米、宽3分米、高4分米，在它的六个面涂绿色，然后锯成棱长都是1分米的小正方体，在锯成的正方体中，三面绿色、两面绿色、一面绿色和没有绿色的小正方体各有多少个？大多数学生看到这样的题目根本无从着手，错误百出。我看到这种现象后是这样处理的：先出示这样一个例题：（右图是27个小正方体拼成的 一个大正方体，把它的表面全部涂成绿色，请想一想：没有涂到颜色的小正方体有多少块？一面涂色的小正方体有多少块？两面涂色的小正方体有多少块？三面涂色的小正方体有多少块？这一题对大多数学生来讲不是很难，反馈后得出几个结论：没有涂到颜色的小正方体一定在正方体的中间；一面涂色的小正方体一定在每个面的中间；两面涂色的小正方体一定在每条棱的中间；三面涂色的小正方体一定在每个顶点上；当学生自以为找到了问题的实质，有点沾沾自喜时，我出示了自己编的第二题（如果是64个、125个……小正方体拼成的 一个大正方体，把它的表面全部涂成绿色，请想一想：没有涂到颜色的小正方体有多少块？一面涂色的小正方体有多少块？两面涂色的小正方体有多少块？三面涂色的小正方体有多少块？）这时候大部分学生傻眼了。我及时引导利用表格进行探究：

学生探究后讨论得出了以下规律：三面涂色的小正方体一定是8个；二面涂色的小正方体块数=（棱长-2）×12；一面涂色的小正方体块数=（棱长-2）×（棱长-2）×6；没有涂色的小正方体块数=（棱长-2）×（棱长-2）×（棱长-2）。这时学生欣喜若狂，我出示了学生做错的题：一个长方体木块长5分米、宽3分米、高4分米，在它的六个面涂绿色，然后锯成棱长都是1分米的小正方体，在锯成的正方体中，三面绿色、两面绿色、一面绿色和没有绿色的小正方体各有多少个？题目一读完，学生纷纷举手回答，并得出了以下规律：三面涂色的小正方体一定是8个；二面涂色的小正方体块数=【（长-2）+（宽-2）+（高-2）】×4；一面涂色的小正方体块数=【（长-2）×（宽-2）+（宽-2）×（高-2）+（长-2）×（高-2）】×2；没有涂色的小正方体块数=（长-2）×（宽-2）×（高-2）。这时的学生兴奋到了极点，脸上都露出了胜利的笑容。

让学生利用错题资源学会“反思”，通过反思优化，进一步加深对立体图形的正确理解。纠正自己对空间关系的错误认识，发现问题，及时改正，逐步修正，从而逐步提高空间想象思维能力。