找准接榫点，巧解综合题

怀铁燕

【摘要】“彼节者有间，而刀刃者无厚；以无厚入有间，恢恢乎其于游刃必有余地矣”解题也有此理，数学知识之间具有纵向的联系，这些知识虽同属不同分支，但可以依靠知识间的内在逻辑关系实现整合，在综合题所呈现的知识网的“榫卯”处加强认知，可化解难点，提高学生解题能力.一、分解组装，暴露接榫点，感受综合题目的形成过程；二、整体呈现问题，挖掘接榫点，形成解析策略

【关键词】知识接榫点；分解组装；整体认知

榫指框架结构两个或两个以上部分的接合处，凹凸咬合浑然天成.数学知识之间具有纵向的联系，这些知识虽同属不同分支，但可以依靠知识间的内在逻辑关系实现整合.数学的综合题就是打破章节界限，跨越两个或几个知识块，需要一定的计算和推理才能解决的问题，注重考查数学知识的整体性，考查综合运用知识的能力和迁移能力是主要出发点.因此在综合题所呈现的知识网的“榫卯”处加强认知，可化解难点，提高学生解题能力.

一、分解组装，暴露接榫点，感受综合题目的形成过程

当各种综合题琳琅满目的出现在学生面前，应接不暇、束手无策、避之不及是自然反应.展示问题的组成过程，可以引导学生领会出题的规律，分解出基本知识点，解开神秘面纱.

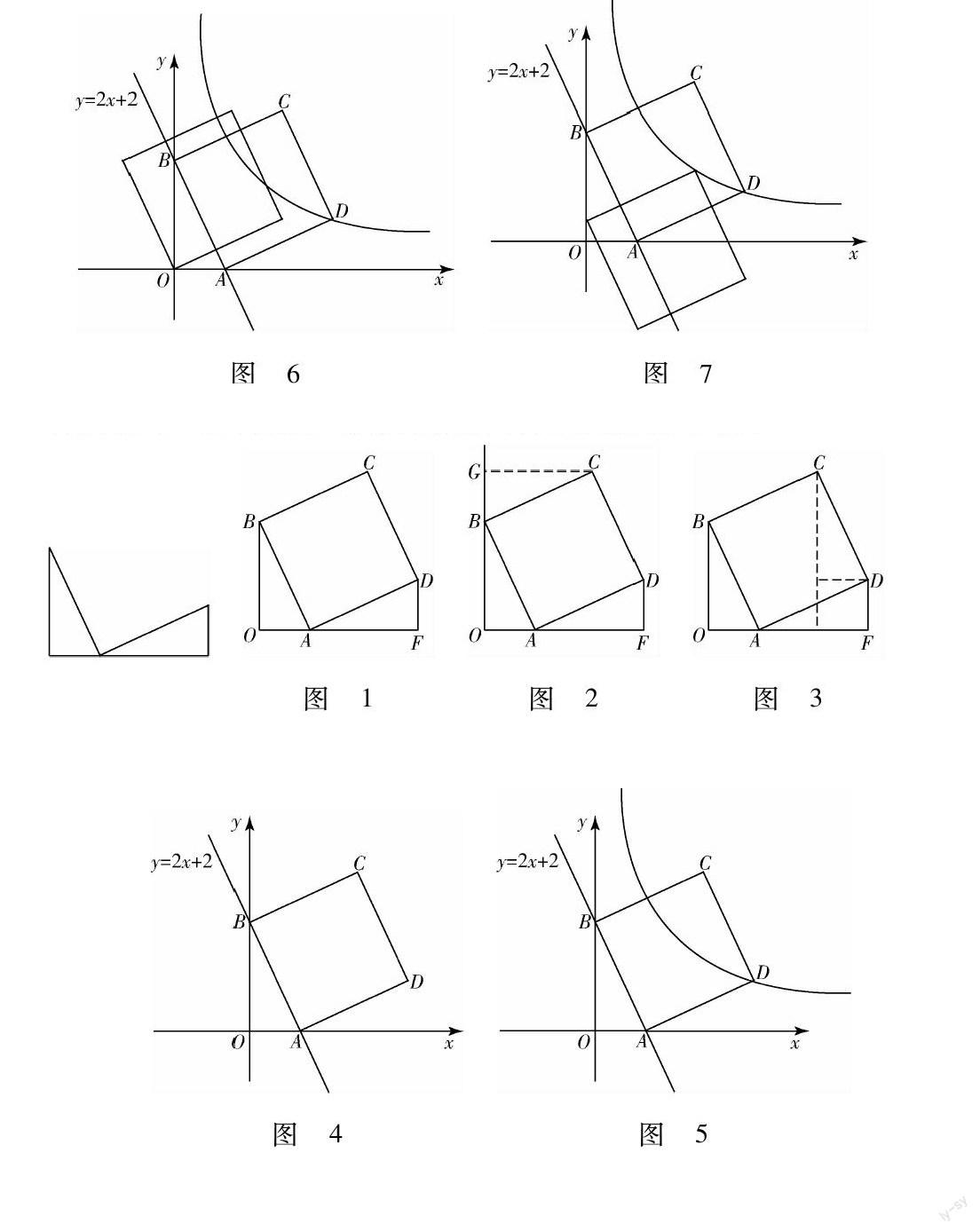
例1如右图所示正方形加两条垂线段所形成的“K”型全等是非常基本的几何图形，经常利用同角的余角相等形成AAS来产生OF=BO+OA等一些数量关系.如果教师在挖掘问题的深度可以预想到提问：点C到线段OF，OB的距离？便可以引入两种常见辅助线重构“K”型全等或“旋转式全等”达到线段转移来获解问题答案.如下图：

图1

图2图3

这时BO与OF的垂直关系及相关线段的长度的获取就是榫眼，它为函数的介入提供空间（如图4）直线AB的解析式为y=-2x+2，前面图1相关的距离可以迁移为求点的坐标如点D、点C，转化思想悄然生成.选择典型的点可确立需要的函数图像（如图5），很自然的求出双曲线的解析式.学生亲历综合题的组装过程，会感觉和直接给全题不一样，不会再有距离感，又品味着环环相扣独特数学逻辑魅力.

图4图5

教师顺势引入图形的平移变换，变换引发的位置改变使图形活起来，但平移变换的性质而产生不变的元素为函数图像上点坐标的读取提供了条件，坐标的获得又为平移变换提供相关数据，如平移的距离.这时即可以提出问题如图6：当正方形ABCD向左平移几个单位点C可落在双曲线上，或问：正方形ABCD向左平移1个单位，点C可否落在双曲线上？学生感觉知识的结合点的存在，各个知识点间相互制约又相互作用，体会到数和形的巧妙融合，难点问题的的高度降下来了，解题能力就提高了.如果教师在能够变式设计或引导学生变式：当正方形ABCD向下移动刚才的问题该怎样解决，学生的识图能力及类比、转化能力，探究意识又会增强.如图7.

图6图7

庖丁说“始臣之解牛之时，所见无非牛者.三年之后，未尝见全牛也”“彼节者有间，而刀刃者无厚；以无厚入有间，恢恢乎其于游刃必有余地矣”解题也有此理，解题快者，读题后可迅速拆分，在接榫处进退自如，所以教师选取典型问题进行分解组装，强化认知知识结合点，感受综合题目形成过程，可使学生感受知识的契合自然巧妙，所参与的往往都是某一知识块最基本的知识点.消除畏惧情绪，提高解题速度.

二、整体呈现问题，挖掘接榫点，形成解析策略

就像喜欢拆装组合玩具一样，学生经历了上述过程后会对综合问题有很大的兴趣也会有信心，但是一旦由他们独立进行挑战完整的问题时，还需积累一系列分析问题的经验.

1.基础知识的掌握要非常扎实，能够迁移、变通

相关概念、定理、公式、基本图形、常用结论，基本技巧和方法是形成综合问题的基石，也是学生解决问题思路的来源，在教学过程中各个环节有意的渗透，还要通过习题的设计使其融会贯通.

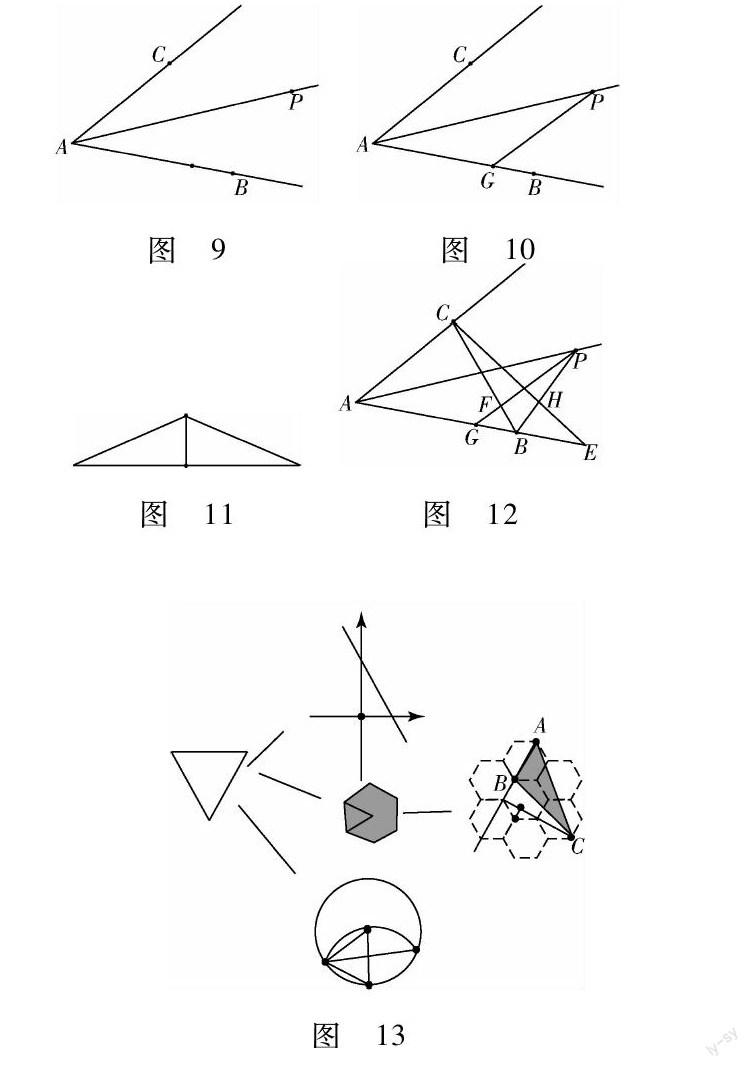
例2见角平分线想到角两边的垂线段；见角平分线、平行线、等腰三角形其二必知另一；见等腰三角形一条重要线段必联想三线合一，见垂直想勾股定理、面积、相似等，并设计恰当的榫点在恰当的时机给出组合图题进行提升训练：如图，∠BAC与∠CBE的平分线相交于点P，BE=BC，PB与CE交于点H，PG∥AC交BC于F，交AB于G，下列结论：①GA=GP；②S△PAC：S△PAB=AC：AB；③BP垂直平分CE；④FP=FC；其中正确的判断有（）.

A.只有①②B.只有③④

C.只有①③④D.①②③④

图9图10

图11图12

学生慢慢的能够将图形看出“3D”效果，有了层次感，也就有了解题的灵感.

图13

重要的基本图形的元素蕴含的基本信息不能有效的传导，也是阻碍学生找到“榫点”并快速产生思路的原因，学生认知往往停留在表层或所学部分知识的背景下，换一个情景或换一个设问就找不到原型，或原型的信息对学生的刺激不够强烈.教师在阶段性复习和终结性复习中将重要的基本图形放到不同的背景中，刺激学生产生迁移认知的意识和能力，例如图等边三角形原型认知及辐射图.同时养成学生定期反思、梳理的学习习惯.

对基础知识的掌握的熟练程度直接影响学生能否寻找到综合题的接榫点，从而决定确立解题思路的速度与能力.同时娴熟的基本计算是保障，学习过程中必须明确什么是最基本的，是可生成的，怎样去联想，这也是所有解決综合题的策略之根.

2.“从已知看可知”，“从要证看需知”等综合法与分析法来沟通已知条件与结论

娴熟的掌握了基础知识可以由题目的已知条件看到很多结论，再结合要得到的结论寻找需要的条件，在不断的分析、综合过程中自然的剖析了问题的结构，综合题分成若干个基本题，知识点之间结合处一个个被挖出来，长时间实践反思，会悟出一套有效地解题策略.

3.数学思想是知识点结合处的润滑剂，也会是解题的灵魂

转化思想是核心思想，结论——需求——已知——可知——结论的任何一个环节产生的联系都离不开转化思想；方程思想利用量与量间外显或隐含的等量关系求取数据的重要方法、工具；分类思想探讨出现结论问题的的一切可能性，从而使问题完整；数形结合可由抽象的数据需要去寻找需要的图形，由图形联想性质，由性质联想图形，使问题得以解决等等.当所有知识都遗忘时，影响人一生的是解决问题的思想方法.数学思想方法的领悟使所学知识不再是零散的点，而是有序的知识链，教学中不断地渗透、明确，内化为需要，成为解题自然方法.

掌握一台机器的构造和性能，最好的办法就是拆了后逐个零件研究，然后再装配.这是“由整体到部分，由部分到整体”的认识事物的规律.展示分解组装题目过程可暴露数学知识间的接榫处，利于找到解题的切入点；扎实的基础背景，巧妙的思想方法，科学的分析策略可以形成独立分解组合题目的能力，不但可以解决问题，长期积累反思，还可以变式思索甚至自创问题，在问题解决中不但锻炼了思维，而且能够更好的感受数学的魅力，实现新课程总体目标就不是难事，学生受到良好的数学教育也不是空谈.

【参考文献】

[1]钱佩玲数学思想方法与中学数学[M].北京：北京大学出版社，2008.

[2]史宁中.数学的基本思想[J].数学通报，2011（1）：50.

[3]董建功.如何命数学题[M].上海：华东师大出版社，2010.

[4]义务教育数学课程标准（2011版）.