“表面涂色的正方体”数学内涵探讨
金震宇
一、前 言
“表面涂色的正方体”是小学数学教学中受广泛关注的内容. 有些版本教材在小学三年级就涉及该内容,也有到初中一年级才出现.
我国小学版数学杂志已有较多文章或教案讨论该课题,这些都是老师们辛勤工作的教学经验总结,十分可贵. 我是小学六年级学生,本学期苏教版采用了“表面涂色的正方体”内容,该内容对我很有吸引力,它使我加深了立体空间概念,启发我从空间图形中去寻找规律,并且尝试用数学思维寻求规律,这是从实际上升到理论,从个别提高到一般的极好教学典范章节.
“表面涂色的正方体”又好像一个“数学魔方”, 使我从中得到乐趣和启发,我们能在玩转这个“数学魔方”中,深入探讨其内涵,会在游戏中增长知识和创新能力,以及理论联系实际的能力.
二、从实际空间图形中去寻找数学表示
教材中要求我们要回答下列几个问题:把一个表面涂色的大正方体,将其2份、3份、4份、5份……n份切开,分别能切成多少个同样大小的正方体?其中3面涂色、2面涂色、1面涂色、无色各有多少个?它们分别处在大的正方体的什么位置?小正方体个数随n的变化数学表示是什么?
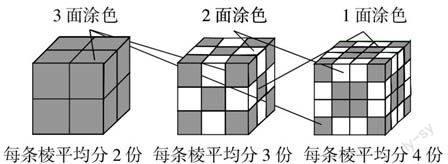
首先让我们从大的正方体每条棱平均分成2份、3份、4份寻找规律,请参见图1.
图1 大的正方体每条棱平均分成2份、3份、4份涂色,小正方体分布,其中红色为3面涂色小正方体,黄色为2面涂色小正方体,蓝色为1面涂色小正方体,无色处于大的正方体剥除所有被涂色的小正方体外表层中间.
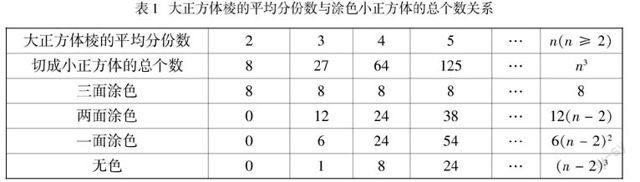
大正方体中切成小正方体的总个数,以及3面涂色、2面涂色、1面涂色、无色小正方体的总个数如表1所示,其位置已在图1标出.
表1所有数值和表示是怎样求得的呢?我是这样分析的:
1. 求大正方体中切成小正方体的总个数,只要把小正方体视为度量单位,就类似求正方体体积一样,求得n3.
2. 3面涂色切成小正方体的总个数无论是大的正方体每条棱平均分成2 份、3份、4份,…,n份,它们只出现在大正方体的8个顶点处,所以与大的正方体每条棱平均分分法无关,都为8个. 在图1中它们都以红色涂面表示.
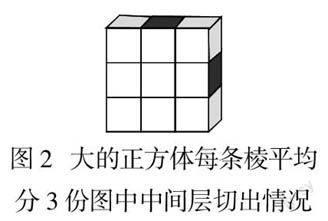
3. 求2面涂色切成小正方体的总个数略麻烦些,它们从大正方体每条棱平均分成3份,及以上才出现,而且它们都出现于大正方体的中间层,本文图2中表示大的正方体每条棱平均分成3份,在其上、下、左、右面切出的中间层展示图,该截面清晰显示有4个2面涂色切成小正方体它们分别位于截层的4角上. 用同样分析方法,我们还可以在大的正方体每条棱平均分成3份的前、后、左、右横切截面各自找到4个2面涂色切成的小正方体,以及大的正方体每条棱平均分成3份的前、后、上、下竖切截面各自找到4个2面涂色切成的小正方体. 所以大的正方体每条棱平均分成3份的大的正方体共有4 × 3 = 12(个)2面涂色切成小正方体.
若大正方体每条棱平均分成4份,从图1可见,仅是又增加了图2中三个中间层,即又增加了12个,即12 × 2 = 24(个).
容易推论,若大正方体每条棱平均分成n份,2面涂色小正方体的总个数可写为:12(n - 2)的一次方关系,括号中减2是来源于2面涂色小正方体层数总比每条棱平均份数少2.
4. 求1面涂色切成小正方体的总个数很简单,从图1可见(蓝色小方块),它们都位于大正方体6个面的中间,大的正方体每条棱平均分成3份时,每个面仅1个1面涂色切成小正方体,故总数为6个.
但是大的正方体每条棱平均分成4份时,因为小正方体一边份数比每条棱平均分成4份数少2个,所以一个面小正方体的个数为(4 - 2)2 = 4个,是2次方增加. 大正方体因为有6个面,所以大的正方体每条棱平均分成4份小正方体的总个数为:6(4 - 2)2 个.
容易推论,若大正方体每条棱平均分成n份,1面涂色小正方体的总个数可写为:6(n - 2)2的2次方关系.
5. 无色小正方体全部位于大正方体中心部,如移走大正方体最外层所有涂色小正方体,无色小正方体总数形成正方体出现. 大的正方体每条棱平均分成3份时,与上文讨论一样原因,无色小正方体仅(3 - 2 =) 1个,如大的正方体每条棱平均分成4份时,无色小正方体增为(4 - 2)3 = 8(个). 大的正方体每条棱平均分成5份时,无色小正方体增为(5 - 2)3 = 27(个). 它们和体积增加类似,是3次方增加.
容易推论:若大正方体每条棱平均分成n份,无色小正方体的总个数可写为: (n - 2)3的3次方关系.
三、玩转这个“数学魔方”,深入探讨其内涵
1. 我发现在大正方体表面拿走一块小正方体,因小正方体所处环境不同,引起大正方体表面积总面积逐级以2个小正方面面积减少规律:
拿走一块一面涂色小正方体,大正方体表面积增加4个小正方面面积;
拿走一块两面涂色小正方体,大正方体表面积增加2个小正方面面积;
拿走一块三面涂色小正方体,大正方体表面积不变;
拿走一块暴露出四面小正方体,大正方体表面积减少2个小正方面面积;
拿走一块暴露出五面小正方体,大正方体表面积减少4个小正方面面积;
拿走一块暴露出六面小正方体,大正方体表面积减少6个小正方面面积。
总之如上随小正方体暴露面增加,它拿走后大正方体表面积总面积逐级以2个小正方面面积减少的规律相应逐减.
其对应关系:
拿走一块小正方体 1面 2面 3面 4面 5面 6面
增加小正方面面积 4个 2个 0个
减少小正方面面积 2个 4个 6个
该规律不限于表面涂色的正方体,对于讨论整齐堆积若干小长方体或正方体形成的总表面积都适用.
如上规律有实际应用价值,可指导人们怎样堆积或取走有污染的小正方体.
2. 如图3,长方体涂色切成小正方体有何变化规律?留给读者思考.
3. 小学低年级同学想一想下面几个问题:
(1)如上文所述,随小正方体暴露面增加,它拿走后大正方体表面积总面积逐级以2个小正方面面积减少的规律相应逐减,用正、负数表示这种逐步变化.
(2)n ≥ 3的“数学魔方”一个面有几个对称轴?
(3)n ≥ 3的“数学魔方” 1面涂色切成小正方体的总个数占涂色小正方体的总个数6n2的几分之几?
(4)产生随小正方体暴露面增加,它拿走后大正方体表面积总面积逐级以2个小正方面面积减少的规律相应逐减的几何原因是什么?
4. 初一同学能以更高数学方法表述该“数学魔方”,很值得期待.
5. 高一老大哥玩转这个“数学魔方”有用武之地吗?应该有!
【参考文献】
[1]朱耀峰.“表面涂色的正方体”教学设计与思考.教育研究与评论:小学教育教学,2014(6):62-63.
[2]数学.六年级上册.江苏教育出版社,2014(6):26-27.

