基于改进GM（1，1）模型的居民消费价格指数的预测

卯青叶

摘要：由于居民消费价格指数受多方面因素的影响，单纯地采用GM（1，1）模型无法准确地进行预测，因此，文章提出改进GM（1，1）模型。首先，以2009～2013年居民消费价格指数为基础，通过建立普通GM（1，1）模型对2009～2013年居民消费价格指数进行模拟，发现模拟值与真实值之间存在差异较大;其次，基于普通GM（1，1）模型对残差进行修正，求解得到改进后的GM（1，1）模型，并对改进后模型进行可行性验证;最后，根据求解得出的改进GM（1，1）模型，对未来几年居民消费价格指数进行预测。结果表明，该预测方法是可行的，为其他相关预测提供了一种理论依据。

关键词：居民消费价格指数;GM（1，1）模型;残差修正;预测

一、引言

CPI是居民消费价格指数（consumer price index）的缩写。它作为一种宏观经济指标，反映了居民家庭购买商品能力以及服务价格水平波动情况。居民消费价格指数不仅影响着人民群众的生活，而且也关乎着整个国民经济价格体系。作为经济分析、决策和国民经济核算的一个重要指标，它的变动率从某种程度上反映出通货膨胀或紧缩的情况。因此，居民消费价格指数与居民生活息息相关且影响着居民生活水平，有必要对其进行预测分析。

近年来许多学者对居民消费价格指数进行了研究。比如，卞集利用GARCH模型对我国居民消费价格指数的波动性进行了研究，结果表明我国居民消费价格指数所代表的通货膨胀是通货膨胀的Granger原因，而非其波动性;曹晓俞利用时间序列模型对居民消费价格指数进行分析研究，并从中选出预测精度相对较高的模型对我国未来一段时间内的居民消费价格指数水平进行了预测;李加兵等通过数理统计模型对居民消费价格指数进行了应用研究，并对周期项的预测效果进行了改善;于扬依据ARMA（p，q）模型的内在机理导出了其点预测和区间预测的计算公式，并对我国居民消费价格指数进行了短期预测;李隆玲等建立了ARIMA模型对2014年中国居民消费价格指数进行了预测分析，并检验了预测模型的精度。以上学者都为居民消费价格指数的预测分析做出了贡献，然而从精度上考虑，这些学者所建模型的精度不是很高，因此预测值和真实值之间将会有一定的差距，为了进一步提高预测精度，有必要对模型加以改进。

为进一步提高预测精度，缩小预测值与真实值之间的差距，本文提出对普通GM（1，1）模型进行残差修正，并检验改进模型的可靠度，如果模型符合预测要求，则可以用来预测未来几年居民消费价格指数。

二、基于残差修正的GM（1，1）模型建立的方法与步骤

（一）传统GM（1，1）模型的建立

传统GM（1，1）模型的步骤主要分为五步来完成。

1. 原始数据累加。设原来数据序列为

X（0）={x（0）（1），x（0）（2），…，x（0）（n）}（1）

式中x（0）（i）≥0，i=1，2，…，n。将原始数据进行一次累加生成，一则可以弱化它的随机性，二则可以加强其规律性，从而得到生成后的序列为

X（1）={x（1）（1），x（1）（2），…，x（1）（n）}（2）

式中x（1）（k）=∑ki=1x（0）（i），k=1，2，…，n。

2. 均值生成。将累加后的数列（2）按照公式（3）作紧邻平均值，可得如下序列。

Y（1）={y（1）（1），y（1）（2），…，y（1）（n）}

Y（1）（k）= [x（1）（k）+x（1）（k-1）]，k=2，3，…，n（3）

3. 传统GM（1，1）模型的建立。根据X（1）={x（1）（1），x（1）（2），…，x（1）（n）}建立GM（1，1）模型，则对应的白化微分方程为

+ax （t）=ux （1）=x （1）（4）

式中a、u为待辨识参数。通过常微分方程理论中Laplace变换的方法，可以求得方程（4）的解析式为

X（1）（t）=[x（1）（1）-a/u]e-a（t-1）+a/u（5）

运用最小二乘法可以估计出a、u值为

a^=[a，u]T=（BTB）-1BTyN（6）

式中

B=- [x （1）+x （2）]     1- [x （2）+x （3）]     1┇        ┇   - [x （n-1）+x （n）] 1 （7）

yN=[x（0）（2），x（0）（3），…，x（0）（n）]T（8）

将a、u最小二乘法解代入方程（5），可以得到近似解，即

X^（1）（t）[x（1）（1）-a/u]e-a（t-1）+a/u（9）

取其离散形式可得式（10），即

X^（1）（k）=[x（1）（1）-a/u]e-a（k-1）+a/u，k=1，2，…，n（10）

然后将其还原为原来数列，即GM（1，1）模型的动态预测模型，为

X^（0）（k+1）=X^（1）（k+1）-X^（1）（k）（11）

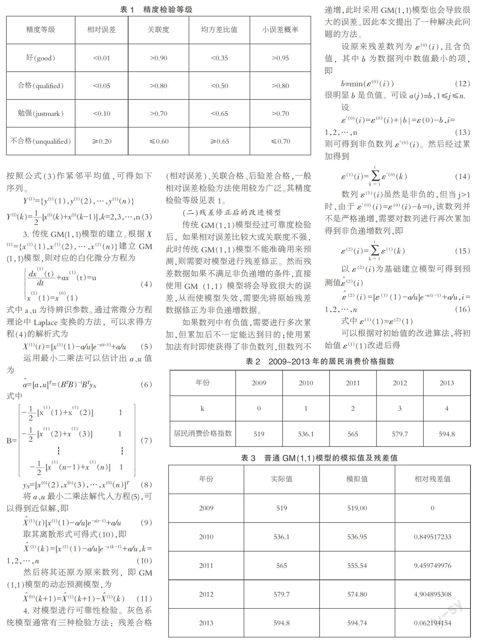
4. 对模型进行可靠性检验。灰色系统模型通常有三种检验方法：残差合格（相对误差）、关联合格、后验差合格，一般相对误差检验方法使用较为广泛。其精度检验等级见表1。

（二）残差修正后的改进模型

传统GM（1，1）模型经过可靠度检验后，如果相对误差比较大或关联度不强，此时传统GM（1，1）模型不能准确用来预测，则需要对模型进行残差修正。然而残差数据如果不满足非负递增的条件，直接使用GM（1，1）模型将会导致很大的误差，从而使模型失效，需要先将原始残差数据修正为非负递增数据。

如果数列中有负值，需要进行多次累加，但累加后不一定能达到目的;使用累加法有时即使获得了非负数列，但数列不递增，此时采用GM（1，1）模型也会导致很大的误差。因此本文提出了一种解决此问题的方法。

设原来残差数列为ε（0）（i），且含负值，其中b为数据列中数值最小的项，即

b=min（ε（0）（i））（12）

很明显b是负值。可设a（j）=b，1≤j≤n.

设

ε′（0）（i）=ε（0）（i）+|b|=ε（0）-b，i=

1，2，…，n（13）

则可得到非负数列ε′（0）（i）。然后经过累加得到

ε（1）（i）= ε′（0）（k）（14）

数列ε（1）（i）虽然是非负的，但当j>1时，由于ε′（0）（i）=ε（0）（i）-b=0，该数列并不是严格递增，需要对数列进行再次累加得到非负递增数列，即

ε（2）（i）= ε（1）（k）（15）

以ε（2）（i）为基础建立模型可得到预测值ε^（2）（i）

ε^（2）（i）=[ε（1）（1）-a/u]e-a（i-1）+a/u，i=1，2，…，n（16）

式中ε（1）（1）=ε（2）（1）

可以根据对初始值的改进算法，将初始值ε（1）（1）改进后得

ε^（2）（i）=[ε（1）（1）+θ-a/u]e-a（i-1）+a/u，i=1，2，…，n（17）

式中θ= -x（0）（1）+ ，p= ε（1）（k）e-a（k-1），q=（1-ea）

获得预测值ε^（2）（i）后仍需要经过累减和降值还原

ε^（1）（i）=ε^（2）（i）-ε^（2）（i-1）ε^（1）（1）=ε^（2）（1）i=2，3，…，n（18）

ε^（0 ）（i）=ε^（1）（i）-ε^（1）（i-1）ε^（0）（1）=ε^（1）（1）i=2，3，…，n（19）

ε^（i）=ε^（0）（i）-|b|=ε^（0）（i）+b，i=1，2，…，n（20）

最后得到的ε^（i）就是原来数列ε^（0）（i）的预测值。

三、案例分析

以2009～2013年居民消费价格指数为相关数据，建立火灾损失的GM（1，1）模型以及残差改进后的GM（1，1）模型，并检验模型的可靠性，然后利用改进后的模型预测未来三年的相关数据。原始数据如表2所示。

（一）居民消费价格指数普通预测模型

根据上面公式，可以计算得到a=-0.0351，u=-0.0021，则得到时间响应函数为

x^（1）（k+1）=502.46e0.0351k+16.54，k=0，1，…，n

则根据模型可得模拟值及残差值如表3所示。

经检验平均相对误差为α=0.21，根据表1可得，该模型不合格，因此无法作为预测模型进行预测。

（二）居民消费价格指数的改进预测模型

由表3可以看出，普通GM（1，1）模型模拟出的数值与真实值之间的残差值较大，因此有必要对残差值进行改进，缩小与真实值之间差距。此时，可以把残差值作为初始值，进行二次GM（1，1）模型的建立。残差数据如表4所示。

根据公式（12）至（20），可以得到残差值GM（1，1）模型的a=-0.0051，u=-0.011，则

ε^（1）（i+1）=0.321e0.0051i+0.5，i=1，2，…，n

结合前文中的预测模型，可得残差修正后的模型如下：

x^（1）（k+1）=502.46e0.0351k+0.321e0.0051i+17.04，k=1，2，…，n

由残差修正后的模型可得新模拟值与残差值如表5所示。

经检验平均相对误差为α=0.0072，根据表1可得，该模型符合标准，可以进行预测。则2014～2016年居民消费价格指数分别为602.3、612.5、618.7。2009～2013年居民消费价格指数普通GM（1，1）模型模拟值与改进后模型模拟值比较，如图1所示。

四、 结论

如果数据波动较大时，普通灰色模型不能准确模拟真实值，此时为进一步提高精度，可以进行残差修正，发现残差模修正过的模型模拟出的值与真实值更加接近，经检验改进后的GM（1，1）模型验证结果较好，且对居民消费价格指数的预测精度相对较高，因此可用来预测未来几年的居民消费价格指数。从预测结果可以看出，居民消费价格指数在不断上涨，说明物价在不断上涨，如果政府不采取合理措施及时控制居民消费价格指数的上涨，将很大可能导致通货膨胀。

参考文献：

[1]卞集.我国居民消费价格指数的波动性研究[J].金融经济，2010（12）.

[2]曹晓俞.居民消费价格指数的时间序列模型分析[J].华北金融，2012（07）.

[3]李加兵，常飞，田云飞.数理统计模型对居民消费价格指数的应用研究[J].2014（16）.

[4]于扬.居民消费价格指数近期预测[J].经济论坛，2013（09）.

[5]李隆玲，田甜，武拉平.中国居民消费价格指数预测[J].农业展望，2014（07）.

[6]景国勋，施式亮.系统安全评价与预测[M].北京：中国矿业大学出版社，2009.

[7]陈宝智.系统安全评价与预测[M].北京：冶金工业出版社，2005.

（作者单位：河南理工大学能源科学与工程学院）