适时进行数学的美学教育
王强 郑杰
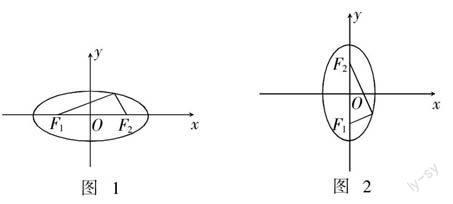
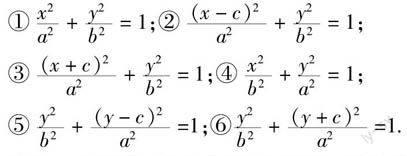
笔者听了本校一位数学老师的一节“椭圆的标准方程”一课,感触颇深. 现将授课实录(片段)和自己的感想记录下来与大家分享.
一、授课实录(片段)
S:同学们,我们已经知道了椭圆的定义,下面我们来推导椭圆的标准方程.
接着,老师在黑板上画出下面两个图形,然后将学生分成两个小组分别求两个图形所对应的椭圆方程. 教师巡视指导.
S:多数同学已经求出椭圆方程,下面请各小组派一名代表展示他们的成果.
学生利用展示台展示推导椭圆方程的过程. 教师给以肯定. 接着进行课堂练习.
二、我的感想
新课程标准明确提出:倡导自主探索、动手实践、合作交流等学习方式,崇尚数学的理性精神,体会数学的美学意义. 我们在教学中应把握好教材,充分利用好教材,创造学生动手实践的机会,适时对学生进行数学的美学教育.
1. 归还学生学习自主权
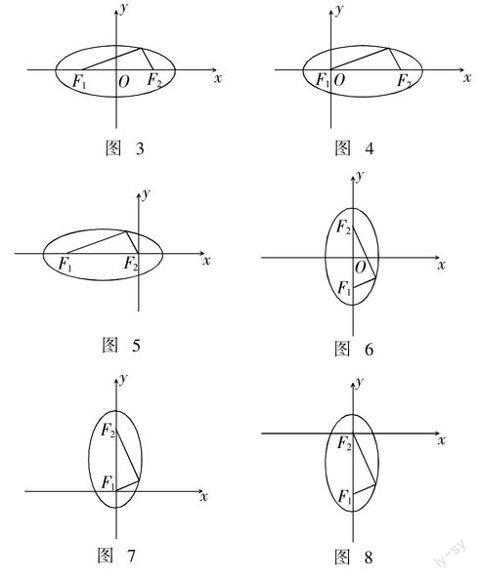
一节好课不在教师教了多少,而是学生学会多少. 放手让学生建立坐标系(学生已经有建立坐标系的基础),学生一定会提出如下面一些图示的建系方法(可能会更多).
让学生主动参与到课堂教学中来,成为学习的主人. 拓展他们的思维空间,不要总是按照教师的思路去思考.
2. 创造学生相互交流与合作的机会
让每名学生都参与到教学中来,本节课(针对六个不同的图形)应把学生分成六个小组,组内每名同学都发表自己的见解,大家合作探究推导出椭圆方程(教师巡视指导). 六个图形对应的椭圆方程如下:
推导一个图形对应的方程用了很长时间,推导六个方程用时会更多. 让学生逐渐明白一个道理,一个人的单打独斗很多事做不了. 团队精神、合作意识应根植于每名学生心中.
3. 树立学生学好数学的信心
待各小组推导出椭圆方程后,请各小组派一名代表展示他们的成果(利用展台). 教师及时作出评价,让学生们体验成功的喜悦,增加学习数学的兴趣,树立学生学好数学的信心.
4. 适时进行数学的美学教育
观察六个图形对应的椭圆方程,为什么图1和图4对应的方程最简单哪?(学生通过观察容易得出:图2、图3只关于x轴对称,图5、图6只关于y轴对称,而这图1、图4关于x轴、y轴、原点都对称,所以方程形式最简单,充分体现数学的对称美. )
观察六个图形,看它们有怎样的关系?(学生通过观察容易得出:六个图形只是在坐标系中的位置不同,图1经过平移可以得到图2、图3,图4经过平移可以得到图5、图6,图4经过旋转可以得到图1. 这充分体现数学的统一美. )
美是人人都愿意追求的,没有人不爱美. 生活中有美,数学中也有美. 数学图形的对称美,数学符号的简洁美,图形与图形间的差异美与统一美在本节课中都有体现,教师应抓住机会适时进行数学的美学教育,激发学生学习积极性,使学生在轻松愉悦的氛围中尽享数学的美.

