超级画板动态展示，几何直观特殊到一般

张天宁

【摘要】在初中阶段几何学习的过程中，有部分定理不需要严格的逻辑推理，只需学生通过动手实践猜想得到定理即可，但是通过超级画板的图形动态展示，几何直观从特殊到一般，使学生对定理的成立有了更深的理解，对学习的促进有了更大的帮助。

【关键词】信息技术  超级画板  相似三角形

2011新课程标准要求：有效的数学教学必须建立在学生的主观愿望和已固有知识的经验之上.按此要求，我在《探索三角形相似的条件》本节课教学主要模式为探索性合作学习. 从学生熟知的知识引入，以三角形全等判定条件为情形，过渡到三角形相似的判定条件的探索. 学生按教师所提出的问题进行思考，并在教师的启发下进行自主探索与合作交流. 最后总结得出：两角对应相等的两个三角形相似的判定条件.通过练习，学会用此结论去解决简的实际问题.

案例片段：

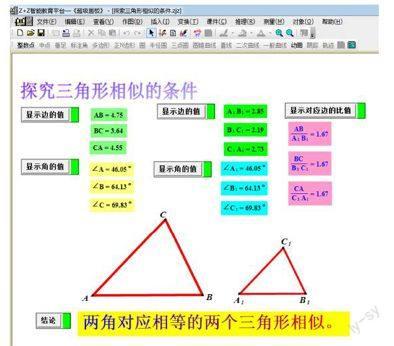
师：通过操作和探索，我们发现：仅有一个角对应相等不能判定两个三角形相似. 请同学们拿出我们做好的另外两个三角形△ABC，使∠A=45°，∠B=60°，另一人画△A′B′C′    ，使∠A′=45°，∠B′=60°，然后比较你们画的两个三角形，∠C与∠C′相等吗？

生1：相等. 因为∠C=75°，∠C′=75°.

师：请各小组成员合作一下，用刻度尺测量一下各线段的长度，并计算对应边的比

生2：（在操作中发现）老师，我们度量的线段的长度的值是近似的，对应边的比值计算出来也是近似值.

师：用刻度尺测量线段长度存在误差是正常的，所以你们小组计算出来的比值也只是近似的其他小组情况如何？

生3：我们的结果与前面小组的结果一样.

师：同学们，你们在计算对应边

师：同学们，你们在计算对应边A′B′（AB），B′C′（BC），A′C′（AC），的值后发现了什么？

生4：经过测量和计算，发现它们这些线段的比是近似相等的.

（请多组同学把他们小组讨论的结果拿到讲台上来展示。）

师：通过刚才探究、合作交流的过程，你们能得出△ABC与△A′B′C′    相似吗？

生5：能得出△ABC∽△A′B′C′    ，这是因为它们满足三角对应相等，三边对应成比例的条件.

师：这个探索过程得到的结果说明了什么问题？

生6：有两个角对应相等的两个三角形相似.

师：上面的结论是否成立呢？还是按前面的分组：请一位同学再画一个△ABC使∠A=20°，∠B=100°，另一位同学画△A′B′C′，使∠A′=20°，∠B′=100°，画完后再互相比较一下.

生7：学生动手实验后，同上面的结论一样.

师：同学们通过两次实验我们能判定两个三角形相似吗？我们通过Z+Z超级画板来一起研究更一般情形.请几位同学上讲台来改变两个角的大小，看看对应边的比值有没有变化。

生8：學生上讲台改变∠A和∠B、∠A′和∠B′的大小。

生9：（学生齐生回答）比值没有变，两个三角形相似。

师：我们可以把这个结论作为判定两个三角形相似的一个条件了.结合图形可以写成如下的

推理过程（板书）：

∵∠A=∠A′，∠B=∠B′，∴△ABC∽△A′B′C′    .

三、思考：

1.在教学中没有采取以往的老师教授的方法，根据数学新课标的要求，我利用学生熟悉的“探索三角形全等的条件”的方法，通过类比的学习方法，在学生动手操作合作交流后，自主探索发现结论.再通过Z+Z超级画板证明一般性，使学生在初中阶段不要求严格推理证明的定理得到了直观验证，鲜明的体现了知识发生、形成和发展过程.

2.本节课有全等三角形类比猜想三角形相似的条件，提高学生的求知欲望。学生参与意识很强，回答问题踊跃，在同学们的动手验证中亲历探索过程，通过超级画板动态演示，更直观的从特殊到一般，在他们的小组合作探究中提高了他们的思考水平，使我们的平时教学的课堂更加高效。

甘肃省教育科学“十二五”规划课题“超级画板支持下的初中数学课堂教学有效性的案例研究”（GS[2013]GHB0466）阶段性成果

【参考文献】

[1]高群安.王巨章 一道竞赛题的巧解、变式与推广[J]-上海中学数学2007（4）

[2]王峰.廖冬 超级画板与几何画板操作简单性比较[J]-中国信息技术教育2009（20）