压力容器筒体上锥形接管开孔补强计算的探讨

韩志威，程涛涛

(惠生工程(中国)有限公司河南化工设计院分公司，郑州 450018)

引言

随着石油化工、煤化工行业装置的大型化以及新技术新工艺的应用，大型化、高设计参数、结构复杂化的设备也逐渐出现，常规设计中难免会遇到新的压力容器开孔结构形式，例如锥形接管、斜锥形接管等结构。而这些开孔结构形式的开孔补强计算在GB150.1 ～150.4-2011《压力容器》［1］及相关标准中均未提及。按照压力容器设计要求，接管开孔补强计算是需要出计算书的。采用分析法固然准确，但需投入大量的时间且要求较高的软件应用技能，因此显得尤为麻烦。根据现有计算模型，可以将锥形接管、斜锥形接管等开孔补强计算进行等量转化，找到适用于工程设计的计算方法。

1 计算模型与补强计算方法

HG/T20582-2011《钢制化工容器强度计算规定》中，第6章针对非径向接管的开孔补强计算，提出了适用于圆筒、锥壳、球壳、凸形封头和平封头在内压或外压作用下装有单个或多个非径向圆形接管(包括球壳和凸形封头的非径向接管、圆筒或锥壳轴向斜接管和周向斜接管、平封头斜接管)的补强计算方法，适用范围为壳体或封头所允许的最大开孔直径(以椭圆孔的短轴计)。按GB150.1～150.4-2011有关章节的规定，采用补强圈进行补强时，钢材的常温抗拉强度、补强圈厚度、壳体或封头名义厚度的限制条件同《钢制压力容器》有关章节的规定。计算模型见图1，采用的计算方法为等面积补强法。

壳体截面因开孔丧失的强度等于被削弱的承载面积乘以壳体材料在设计温度下的许用应力，须有补强材料予以补偿。从补强角度讲，壳体截面由于开孔丧失的拉伸承载面积应在孔边有效补强范围内进行补强。当补强材料与壳体材料相同时，所需补强面积就与壳体开孔削弱的强度面积相等，即等面积补强法。无限大平板开小孔，是容器壳体进行等面积补强的力学基础。［2］补强计算时，在有效补强范围内的所有多余面积(有效厚度提供的面积扣除壳体或接管本身强度所需的面积)均可作为补强面积。［3］

等面积补强法以补偿开孔局部截面的拉伸强度作为补强准则，其补强只涉及静力强度问题。壳体开孔以后，在开孔边缘产生局部高应力。根据局部应力的分布衰减规律，在离开孔边缘较远处，其应力便恢复到正常水平。为有效发挥补强材料的强度，补强材料应设置在开孔附近的高应力区域，即有效补强范围内。有效补强范围存在于开孔壳体和接管两部分。开孔壳体上的有效补强范围是以受拉伸开孔大平板孔边应力的衰减范围进行考虑的，即补强范围取为2倍开孔直径对应的范围。接管上的有效补强范围是以端部受均布载荷的圆柱壳的环向薄膜应力的衰减范围进行考虑的，即补强范围取为(d为开孔直径，δn为接管名义厚度)。

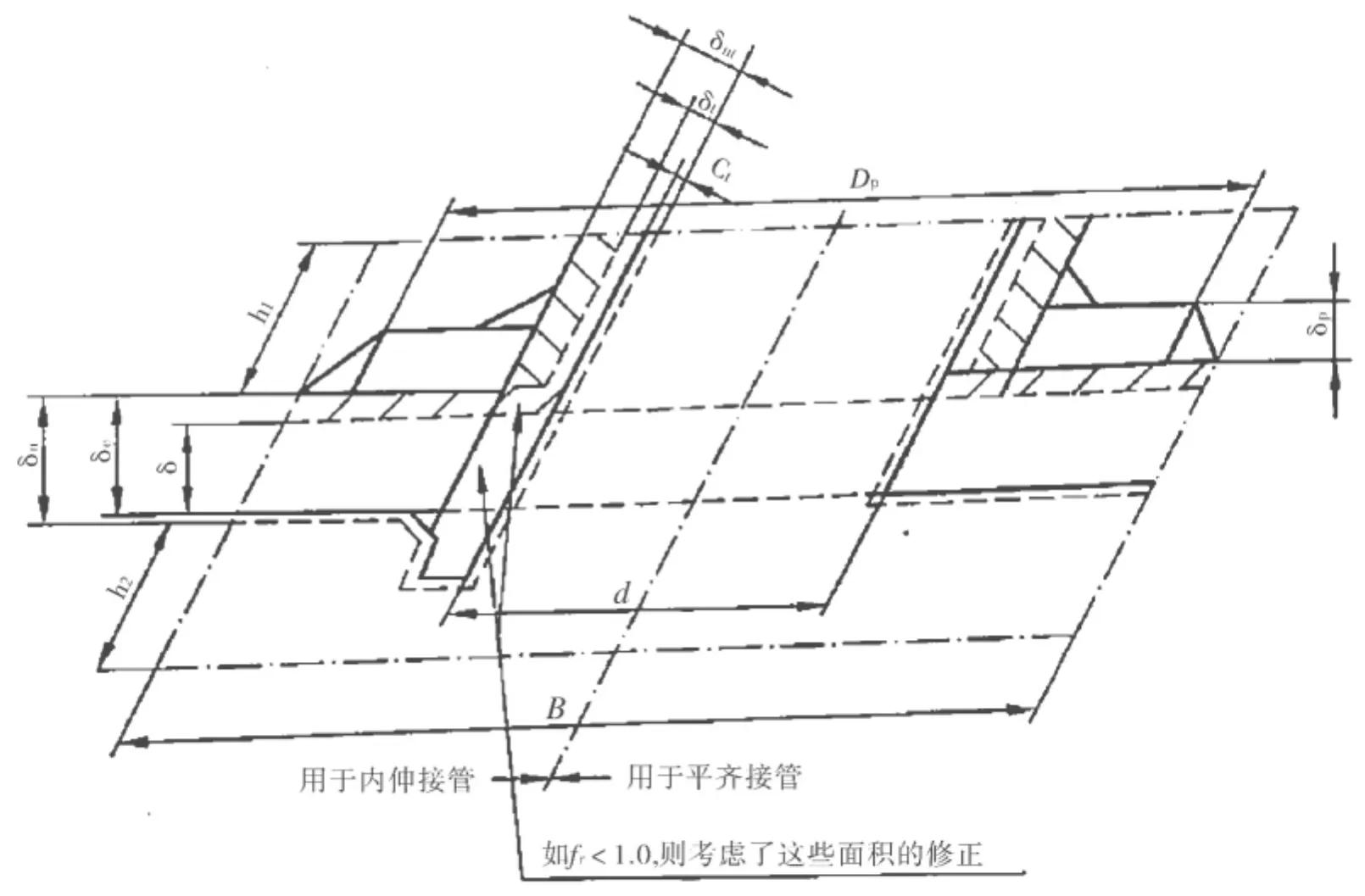
图1 开孔补强计算模型

等面积补强法是以拉伸的开孔大平板为计算模型的，即仅考虑容器壳体中存在的拉伸薄膜应力，且以补强壳体的一次总体平均应力作为补强准则。当开孔较小时，开孔边缘的局部应力以薄膜应力为主，故该方法可适用。随着壳体开孔直径增大，开孔边缘不仅存在很大的薄膜应力，而且还产生很高的弯曲应力，此时该方法不能适用。对于开孔边缘的二次应力的安定性问题，等面积补强法是通过限制开孔形状和开孔范围(开孔率)间接加以考虑的，使孔边的局部应力得到一定的控制。长期的使用经验证明该方法在允许使用范围内，开孔边缘的安定性能够得到保障。等面积补强法对开孔边缘的峰值应力问题未加考虑，为此该方法不适用于疲劳容器的开孔补强。［4］

2 参数分析

本计算的适用范围应满足GB150中的等面积法的适用范围，即适用于压力作用下壳体和平封头上的圆形、椭圆形或长圆形开孔。当在壳体上开椭圆形或长圆形孔时，孔的长径与短径之比应不大于2.0。适用范围如下:

a.当圆筒内径Di≤1500mm时，开孔最大直径d≤Di/2，且d≤520mm;当圆筒内径Di＞1500mm时，开孔最大直径d≤Di/3，且d≤1000mm;

b.凸形封头或球壳开孔的最大允许直径d≤Di/2;

c.锥形封头的最大直径d≤Di/3，Di为开孔中心处的锥壳内直径。

椭圆形或长圆形开孔最大直径d指长轴尺寸。本文就圆筒开锥形接管进行分析计算。以某设备为例，设备要求如下:

筒体直径3000mm，设计压力3.0MPa，设计温度200℃;介质腐蚀裕量为0mm，焊接接头系数取1.0;筒体材质Q345R，设计温度下的许用应力［σ］t=170 MPa;接管材质16MnⅢ，设计温度下的许用应力［σ］tt=150 MPa。

2.1 筒体壁厚

取筒体名义厚度:δn=30mm;

筒体厚度附加量:cs=0.3mm(取钢板负偏差值);

筒体有效厚度:δe=29.7mm。

2.2 开孔直径及壁厚

开孔直径［5］142:为在壳体计算厚度中面上通过开孔中心沿各个所考虑的截面上测至接管内壁的弦长，并加2倍接管厚度附加量的值。现取开孔直径d=400mm。

取接管名义厚度:δnt=50mm;

接管厚度附加量:Ct=0mm;

接管有效厚度:δet=50mm。

2.3 部分参数及符号

有效宽度:B=2d=800mm;

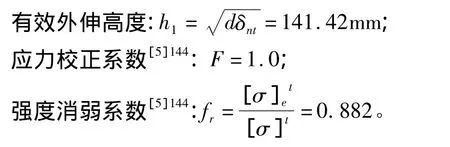
3 补强计算

对压力容器筒体上锥形接管开孔不同结构形式的补强分别按照等面积补强法进行计算。

3.1 “形式1”和“形式2”计算

“形式1”和“形式2”开孔结构见图2，可按照SW6进行计算，计算结果见表1。

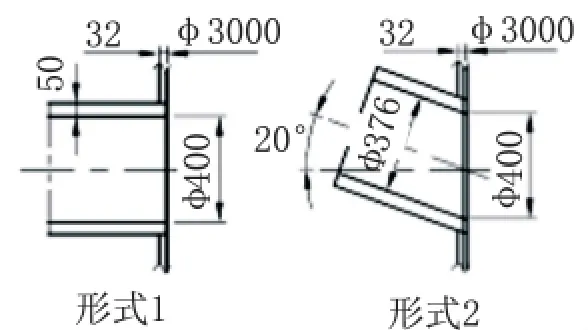
图2 “形式1”和“形式2”开孔结构

3.2 “形式3”计算

“形式3”开孔结构见图3。壳体开孔所需补强面积:

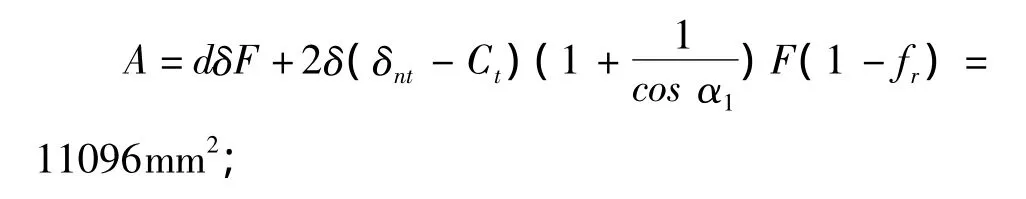
壳体有效厚度减去计算厚度之外的多余面积:

A1=(B-d)(δeφ1-Fδ)-2(δnt-Ct)(δe-Fδ)(1-fr)=1925.5mm2;

接管有效厚度减去计算厚度之外的多余面积:

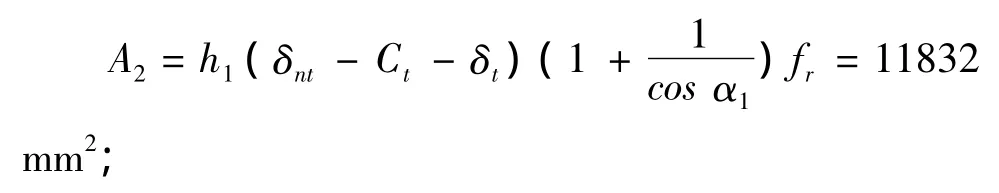
焊缝金属截面积:A3=δw2=100 mm2。

3.3 “形式4”计算

“形式 4”开孔结构见图 3。开孔直径 d=400mm时，梯形上下边长分别为390mm，409.5mm，因此实际计算的开孔直径d＇=(390+409.5)/2=399.75mm。

壳体开孔所需补强面积:

壳体有效厚度减去计算厚度之外的多余面积:

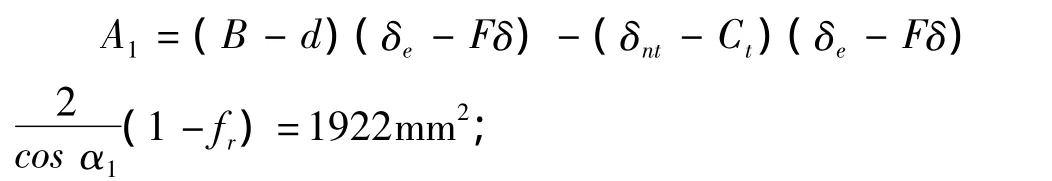
接管有效厚度减去计算厚度之外的多余面积:

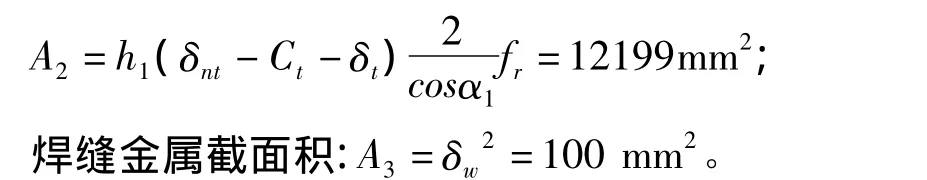
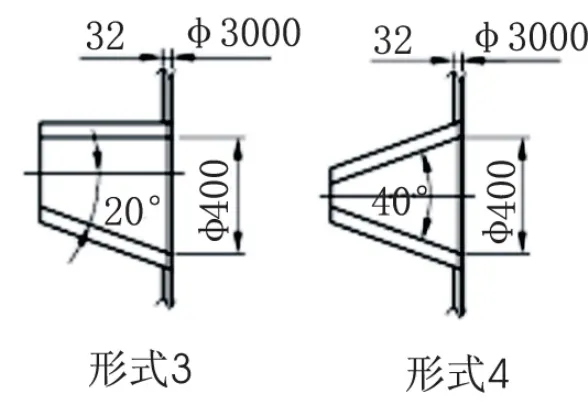
图3 “形式3”和“形式4”开孔结构

3.4 “形式5”计算

“形式 5”开孔结构见图4。开孔直径 d=400mm时，梯形上下边长分别为386mm，413mm，因此实际计算的开孔直径 d＇=(386+413)/2=399.5mm;角度 α1=50°，角度 α2=10°。

壳体开孔所需补强面积:

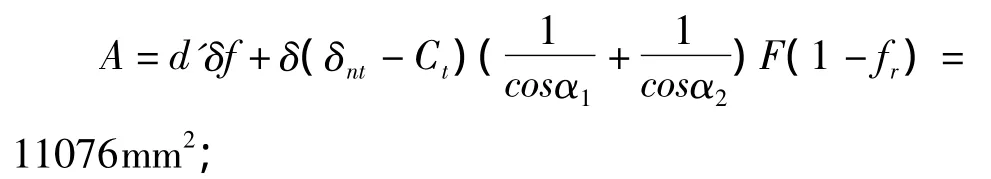
壳体有效厚度减去计算厚度之外的多余面积:

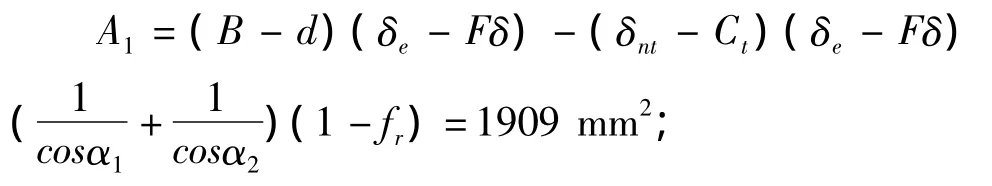
接管有效厚度减去计算厚度之外的多余面积:

焊缝金属截面积:A3=δw2=100 mm2。

图4 “形式5”开孔结构

4 结果对比分析

以上五种锥形接管开孔结构形式补强计算结果汇总见表1。

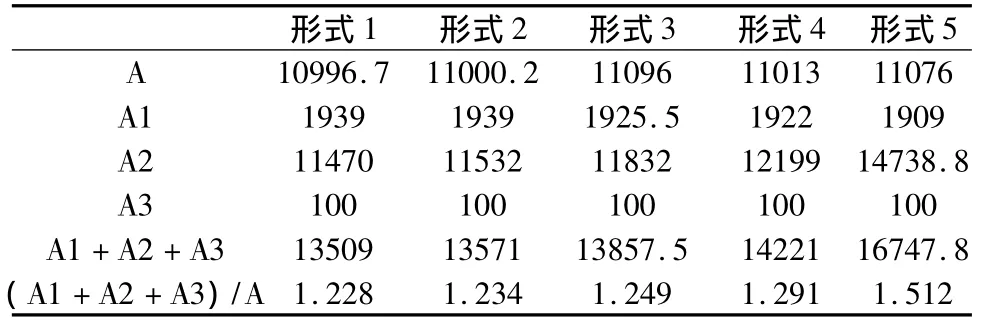
表1 五种开孔结构形式补强计算结果 单位mm2

比较表1中数据不难发现，在开孔直径相同、接管实际外伸高度大于或等于接管有效外伸高度的情况下，径向圆筒形接管(形式1)的有效补强范围内的补强面积和开孔所需补强面积的比值最小。非径向锥形接管(形式5)随着偏转角度的增大而增大，同时也是比值最大的，因此是安全的。

5 结论与建议

通过手算法分别对压力容器筒体上锥形接管五种开孔结构形式进行分析计算，得出了径向圆筒形接管富裕量最小的对比分析。然而实际设计过程中，在筒体壁厚、开孔直径、接管(或锥形接管)壁厚等不确定的情况下进行开孔补强计算，需要花费大量的时间进行试算。手算法固然能保证其正确性，但是从工程设计角度而言，由于项目进度以及人工时成本的控制，必然要求简化计算。因此，在参考上述对比分析计算的基础上，本着安全可靠的思想，可将锥形接管开孔补强计算方法进行简化。

针对按照GB150设计的常规压力容器而言，在满足GB150.3-2011中第6.1.1条等面积补强法的使用范围的前提下(锥形接管开孔直径按当量设计)，建议将锥形接管开孔补强计算转化为按照开孔直径相等的径向圆筒形接管的开孔补强计算，然后再用软件SW6进行设计计算。计算方法如下:

a.根据接管公称直径、压力容器腐蚀裕量及锥形结构形式画图，确定开孔直径;

b.根据开孔直径和预先给定的壁厚，采用SW6进行开孔补强设计计算;

c.如不能满足要求，调整相应参数(如:筒体壁厚、接管壁厚或增加补强圈等)，直至计算结果通过为止。

本文强调的是在满足工程安全可靠前提下的等量转换计算，对于超出等面积法使用范围以及高压容器等关键设备，建议建立模型进行分析设计。

［1］中国国家标准化管理委员会.GB150.1～150.4-2011压力容器［S］.北京:中国标准出版社，2011.

［2］寿比南.GB150-2011《压力容器》标准释义［M］.北京:新华出版社，2012.

［3］王磊.压力容器开孔补强设计方法比较［J］.石油化工设计，2002，19(2):17-19.

［4］杨福昌.壳体径向平齐接管开孔补强之等面积法与盈利分析法［J］.石油化工设备，2013，42:22-25.

［5］中华人民共和国工业和信息化部.HG/T20580～20585-2011钢制化工容器设计基础规定［S］.北京:中国计划出版社，2011.