一种改进的BM算法性能分析
朱保锋,宋 艳
(河南教育学院信息技术系,郑州 450046)
随着计算机应用技术的快速发展,处理非数值数据的应用增长迅速,使得字符匹配问题显得尤为重要,在入侵检测、信息检索、搜索引擎等领域都有所涉及,字符匹配算法效率的高低对搜索引擎在数据查找方面的性能有着非常直接的影响。因此需要找到一种适合、高效的字符匹配算法。
1 BM算法概述
字符匹配是将搜集到的文本信息和数据库中已经存在的模式数据信息进行比较,找出模式串在文本串中的出现位置。当前的字符匹配算法有很多种,例如:蛮力算法、BM 算法、Horspool算法、Wu-Manber算法等。基于字符扫描策略的不同,字符匹配算法可以分为三类:1)从左到右扫描模式和文本每一对相应的字符,一旦不匹配,模式右移一格,进行下一轮尝试,蛮力字符匹配就是该类算法,其平均效率是属于O(n*m)的。2)自右向左匹配文本串与模式串的最大后缀,BM算法、Horspool算法属于此类,BM的最差效率是线性的,Horspool是BM的简化版本。3)自右向左匹配文本串与模式串的最大子串。
1977年,Robert S.Boyer和 J Strother Moore提出了另一种在O(n)时间复杂度内,完成字符串匹配的算法,其在绝大多数场合的性能表现,比KMP算法还要出色,这就是BM算法,一直被认为是最有效的字符匹配算法,开源入侵检测系统Snort就是采用BM算法[1]。但是在BM算法中,有些比较是多余的,降低了算法的执行效率,因此提出一种改进的BM算法,通过实验数据可以表明,改进后的算法能够提高传统BM算法的效率。
2 BM算法的基本原理
BM算法被认为是亚线性串匹配算法,它在最坏情况下找到模式所有出现的时间复杂度为O(mn),在最好情况下执行匹配找到模式所有出现的时间复杂度为O(n/m)。
2.1 定义
定义1:设Σ为字母表,T,P∈Σ+,其中文本串T=t0t1t2…tn-1,模式串 P=p0p1p2…pm-1,m < n。
定义2:c∈Σ且c∈T,c是坏符号,导致模式串P和字符串T的相应字符不匹配;d是模式串相对于文本串移动的距离;k∈N,是文本串与模式串匹配的最大后缀。
2.2 BM算法的工作原理
文本串T与模式串P左对齐,从pm-1开始自右向左,比较文本和模式的相应字符对,如果p0p1p2…pm-1与T中的 titi+1ti+2…ti+m-1一一匹配,则找到了P在T中的出现,返回i,如果模式P超出了文本T,则P没有在T中出现,返回 -1。
模式串P最右边的字符pm-1和文本串T的相应字符c初次比较失败了,模式串P要尽量向右移动足够长的距离[2],以减少移动的次数和比较的次数,降低算法的复杂度。如果c不包含在P的前m-1个字符中,P移动的最长距离为len(P)=m;如果c出现在P的前m-1个字符中(出现的次数有可能>1),此时向右移动P,使P中最右边的c和T中的c对齐,此时P的移动距离是和c相关的。将模式P向右移动的长度用t(c)表示为[3]:

模式串P与文本串T在遇到坏符号c之前,已经有k(0<k<m)个字符成功匹配,模式串P向右移动的长度d参照两个规则:坏符号移动规则和好后缀移动规则。
坏符号移动规则:该规则参照坏符号c,如果c不在P中,将P移动到正好跳过字符c,移动的长度表示为m-k;如果c存在于模式中,将P前m-k个字符最右边的c和T中的c对齐,参照公式(1),P移动的距离表示为t(c)-k。当k相对于t(c)足够大时会导致t(c)-k<0,参照蛮力算法可以使P向右移动1个位置。针对字母集Σ中的每个字符计算坏符号移动表,坏符号移动的距离表示为:

好后缀移动规则:模式串P与文本串T已经匹配的k个字符,称为好后缀,记作suff(k),如果模式P的前m-k个字符中可以找到一个最长字符组合v(len(v)<k)是suff(k)的后缀,移动P使前m-k个字符的最右边的v和suff(k)中的v对齐,此时v是和k相关的。好后缀移动的距离表示为:

取d=max(d1,d2)作为P向右移动的最大距离。
在算法的实现中,事先构建坏符号移动表和好后缀移动表,以减少在不同的c、v和k作用下查找和计算d值的次数,提高效率[4]。
3 一种改进的BM算法
3.1 BM算法的改进
传统的BM算法中存在不必要的比较,当模式串在文本串中的初次匹配失败后,可以根据文本串中当前窗口的下一个字符(即模式串和文本串左对齐后的最右侧字符的下一个字符)决定偏移量,此时只使用坏符号移动规则。如果该字符在模式串中没有出现,最大可以移动的位置为m+1。算法改进后模式向右移动的距离可以用公式4表示:

3.2 BM算法的改进的举例
假设有文本串T和模式串P分别为,P:algorithm,T:this_is_boyer_mbore_algorithms,分析在改进的BM算法中,P匹配T的过程。生成的坏字符跳跃表如表1所示,对于模式P中出现过的字符“algorithm”,其对应的偏移量skip(c)是该字符在模式最右边的出现位置距离模式最右侧字符的长度,其它没有在模式中出现的字符,其偏移量为m+1=10。

表1 坏字符跳跃表
T:this_is_boyer_mbore_algorithms
P:algorithm
第一次匹配:模式串的最右边的字符“m”和文本串中的字符“b”比较,第一次字符比较失败,此时当前窗口的下一个字符为“o”,根据表1知模式串P向右移动的距离为skip(o)=6。
T:this_is_boyer_mbore_algorithms
P:algorithm
第二次匹配:第一次比较模式串中的字符“m”和文本串中的字符“m”,匹配成功,继续比较文本串中的字符“_”和模式串中的字符“h”,匹配失败,此时当前窗口的下一个字符为“b”,根据表1知移动的距离为skip(b)=m+1=10,模式向右移动10个字符的位置。
T:this_is_boyer_mbore_algorithms
P:algorithm
第三次匹配:文本串中的字符“r”和模式串中的字符“m”比较,不匹配,当前窗口的下一个字符是“i”,根据表1,skip(i)=4,模式串 P向右移动4个字符位置。
T:this_is_boyer_mbore_algorithms
P:algorithm
第四次匹配:从模式串的尾字符“m”开始自右向左和文本串的相应字符依次比较,直到k=m,最终找到了模式串在文本串中的出现。
3.3 BM算法的改进前后的比较
根据改进的BM算法思想,抽取数据进行实验验证。在实验中,随机选取了4组样本,模式串的长度基本不变取为8个字符,文本串的字符长度分别选取为500、1000、1500、2000,对于每组样本,分别采用传统的BM算法和改进后的BM算法,得到的字符比较次数和模式串的移动次数的情况如表2所示,每组样本下模式移动次数的情况对比如图1所示。

表2 BM算法改进前后字符匹配时比较次数和移动次数
在实际的字符查找应用中,初次比较不匹配、当前窗口的最后一个字符和下一字符不属于模式串的情况是多数的。在这种情况下,采用改进的BM算法在每次的匹配中可以增加模式串的移动距离,从而减少比较的次数。
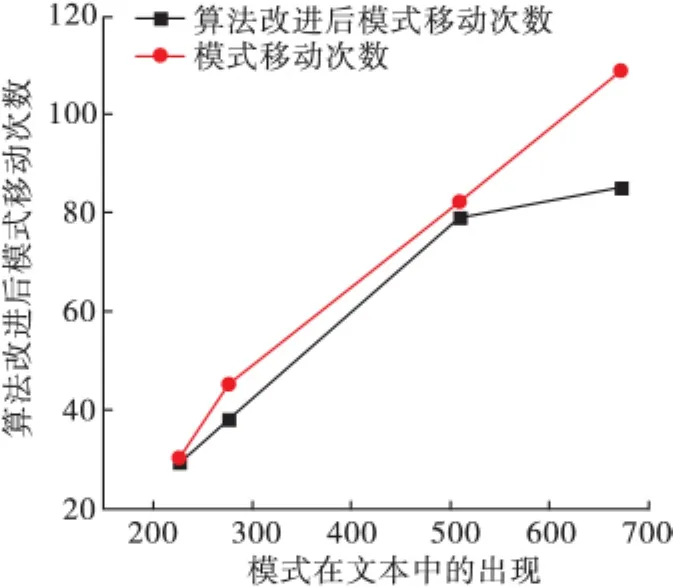
图1 BM算法和改进BM算法比较次数和移动次数对比
4 结论
在传统的BM算法中存在一些不必要的比较,增加了字符匹配时的比较次数,从而在实际的应用系统中导致系统效率不高。在改进的BM算法中,通过结合当前窗口的下一个字符的情况更改模式串的移动距离的长度,可以让移动的距离增加1,最大能够达到m+1。实验数据表明,当文本串相对于模式串足够长,模式串在文本串中的出现次数增加时,可以很大的提高算法的查找效率.
[1]韩光辉,曾诚.BM算法中函数shift的研究[J].计算机应用,2013,33(8):2379-2382.
[2]孙文静,钱华.改进BM算法及其在网络入侵检测中的应用[J].计算机科学,2013,40(12):174-176.
[3]Anany Levitin.算法设计与分析基础[M].北京:清华大学出版社,2007.
[4]李韦男,虞慧群.一种改进的BM字符串匹配算法[J].计算机工程与应用,2014,50(16):104-108.

