CVT 暂态引起距离保护超越的研究

汤馥源，宋仲康，杨芬娜，杨义强

(武汉理工大学 自动化学院，湖北 武汉430070)

电容式电压互感器(CVT)绝缘可靠性高，价格低廉，不易发生铁磁谐振，因此被广泛应用于110 kV 及以上电压等级的输电线路中，作为电压电能的测量元件，为继电保护装置提供可靠的电压信号［1-2］。CVT 中的分压电容可以降低高压输电线路的电压等级，起到一定的隔离作用，但由于其为储能元件，一次电压突变时，二次侧的测量电压会含有暂态误差，可能对保护造成影响［3］。通过故障录波和实验发现，CVT 暂态过程引起的测量误差会造成距离保护的暂态超越［4］，在正向区外和反方向出口发生故障时，保护可能会误动［5-6］。目前已经有很多CVT 暂态对距离保护影响的相关研究，但都是基于距离保护基本原理进行分析的，没有对保护装置中广泛使用的复合距离保护方案进行分析和提出解决办法，也没有定量分析距离保护超越的具体原因。

笔者利用EMTDC/PSCAD 和Matlab 作为仿真工具，对上述问题进行了分析，提出了具体改进方法，并验证了其有效性，解决了CVT 暂态引起的距离保护超越问题。

1 CVT 的等值模型和暂态误差

CVT 主要由分压电容、中间变压器、阻尼器和补偿电抗器等部分组成［7-8］，CVT 等值电路模型如图1 所示。其中U、Ce分别为等效电源电压和等效电容，Rm、Lm分别为中压变压器励磁支路等效电阻和电感，Rb、Lb分别为负载的等效电阻和电感，L1、R1分别为中压变压器一次绕组的漏感和补偿电抗器的等效电感和电阻，rf、Lf分别为谐振电抗器的电阻和电感，Cf为谐振电容，Rf为阻尼电阻。励磁支路的等效电感Lm和电阻Rm值很大，可以等效为开路并在仿真中忽略［9］。

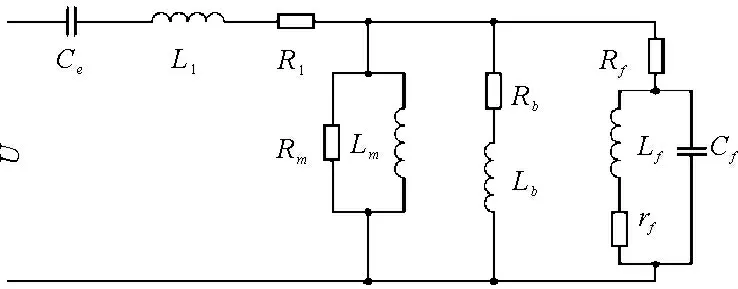
图1 CVT 等效电路图

文献［10］推导出CVT 的暂态误差为：

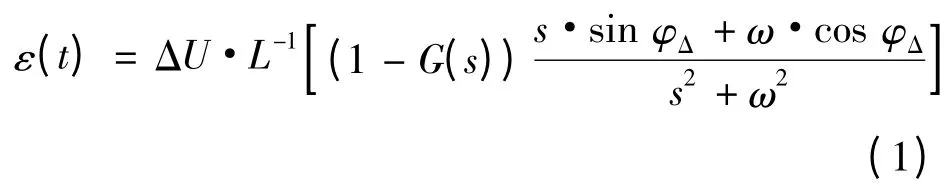
由式(1)可知，暂态误差受短路电压角度和电压变化量ΔU影响。短路电压角度不同时的CVT 暂态特性如图2 所示，在短路电压相角为0°时，CVT 暂态的持续时间最长，对系统的影响最大，因此以下分析都基于短路相角为0°时保护发生故障的情况。

图2 初始故障相角对CVT 暂态的影响

2 距离保护算法

2.1 传统傅氏算法

线路保护装置目前一般使用全波、半波傅氏算法作为采样算法，利用傅氏算法可以求出基波的幅值和相角，进而求出所需其他电气量，构成不同原理的保护［11］，傅氏算法本身具有滤波作用，可以消除非周期分量和高次谐波分量对保护装置采样的影响。

(1)全波傅氏算法：

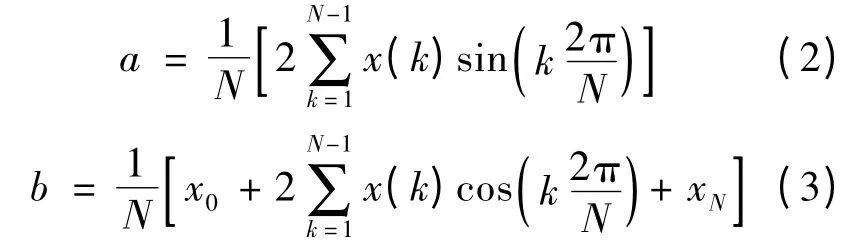
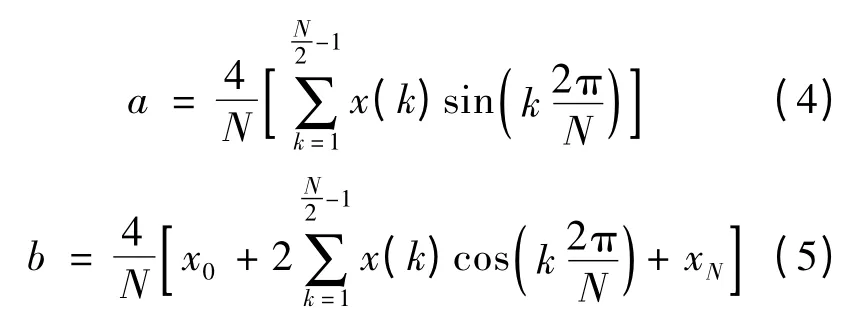
(2)半波傅氏算法：式中：N为基波信号一周期的采样点数;x(k)为第k次的采样值。

2.2 改进半波傅氏算法

半波傅氏算法采样时间短，可以加速保护动作，一般用于切除出口故障和对反应速度要求较高的情况，CVT 暂态引起的超越，主要出现在正反方向出口故障，此时要求保护装置快速识别故障，使用半波傅氏算法效果优于全波，可缩短保护动作时间，但半波傅氏算法滤波能力相对较弱，CVT 暂态过程含有衰减直流分量，使得半波傅氏算法可能无法正确反映故障电压变化。文献［12-13］提出了一种改进半波傅氏算法，使用半个周期外加两个采样点的数据窗长，通过解方程组，求出衰减直流分量的值，从而消除衰减直流分量。图3 是分别采用半波、改进半波和全波傅氏算法时CVT 的暂态电压幅值。

使用改进半波傅氏算法，可以减少CVT 暂态中衰减直流分量对傅氏算法的影响，其暂态峰值和传统半波傅氏算法基本同时出现，但是峰值电压幅值远小于半波傅氏算法，也稍小于全波傅氏算法，总体效果优于传统全波傅氏和半波傅氏算法，并可得出以下结论：

(1)CVT 暂态时采用半波傅氏算法，测量电压幅值会发生短时畸变，峰值电压达到幅值的20%，持续时间为34 ms，与一次侧实际电压相差较大，保护有可能因此发生误动。

(2)采用全波傅氏算法时，暂态持续时间较长，达到49 ms，峰值约为幅值的10%，反应速度慢于半波和改进半波算法。

(3)采用改进半波傅氏算法可以减少暂态持续时间，且电压超越峰值最小，同时其峰值出现时间早于全波傅氏算法17 ms，这在保护中是非常重要的，可利用该特性消除保护误动，且利于保护快速动作。

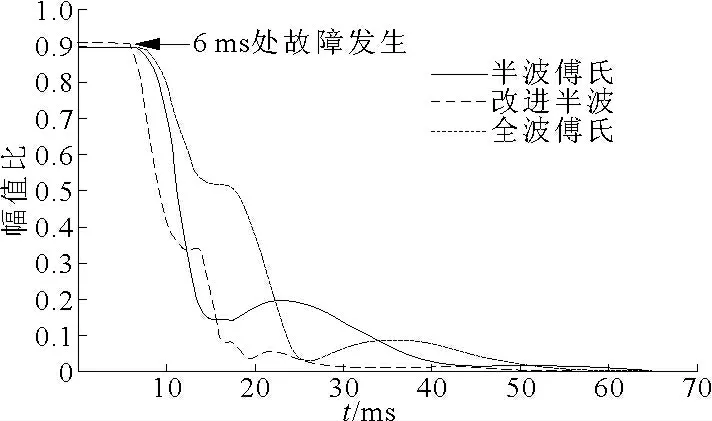
图3 不同傅氏算法下的CVT 暂态电压幅值

3 CVT 暂态引起距离保护超越的原因

3.1 主要距离保护方法

目前我国保护装置主要采用以下两种距离保护方法，第一种为采用比相式欧姆继电器配合低压距离继电器，通过工作电压Uop和极化电压Up比相作动作方程。

接地距离继电器的工作电压为：

相间距离继电器的工作电压为：

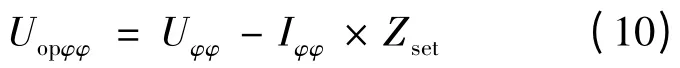
式中：U为继电器测量电压;I为测量电流;Zset为整定阻抗;φ =a，b，c;φφ =ab，bc，ca。使用正序电压U1作为极化电压。当发生区外和反方向非三相故障时，Uop与U同向，区内故障为反向，以防止保护误动;但当发生反方向出口三相故障时，三相电压降为0，使得U1接近于0，保护会失去方向性而发生误动，因此配合使用低压距离继电器，当U1幅值低于启动门槛电压10%UN(UN为额定电压)则进入启动范围，使用两个周波前的记忆电压替代极化电压Up，从而保证距离保护不会误动。

第二种方法是采用多边形特性阻抗元件和小矩形动作区构成复合动作区。其中整定电阻Rset可以使保护兼顾耐受过渡电阻和躲负荷的能力［14］，调整多边形顶边的下倾角度α 可提高躲避区外故障的能力，反方向整定阻抗Zset2的设定可调整其在反方向动作区的特性。为防止出口故障时距离保护因失去方向性误动，使用小矩形动作区作复合判据，当测量阻抗Zm落入动作区域，启动记忆电压判别方向，使距离保护不会误动。

3.2 建模与仿真

仿真使用220 kV 输电线路模型，线路全长100 km，利用EMTDC/PSCAD 进行仿真，主要参数为R=0.035 7 Ω/km，XL=0.507 4 Ω/km，R0=0.303 1 Ω/km，XL0=1.367 0 Ω/km ，XC1=4.50 ×10-6S/km，XC0=2.32 ×10-6S/km。系统阻抗参数为Z0=j14.917 Ω，Z1=j20.254 Ω。仿真数据在Matlab 中进行分析计算，仿真系统模型如图4所示，其中MN侧相角差为0°，距离保护的整定值Zset=0.8Zl，故障类型为0.2 s 时M侧反方向出口和正方向出口分别发生三相短路故障。为了便于仿真，假设测量电流值为准确值，若保护进入动作区大于等于5 ms，则保护启动，分别采用带极化电压的比相式欧姆继电器配合低压距离继电器，四边形阻抗继电器配合小矩形低压保护区的不同保护方案。

图4 仿真系统模型

3.3 仿真结果分析

图5 和图6 为保护出口处发生三相故障时，采用比相式欧姆继电器的保护动作特性图，图7 为采用多边形特性的阻抗轨迹图。由图5 ～图7 可知CVT 暂态引起距离保护超越的主要原因如下：

(1)在反向出口三相短路故障时，采用半波傅氏算法，正序电压U1在故障后10 ms 落入低压距离继电器动作范围10%UN，此时保护不动作。在13 ～23 ms 时，U1幅值超越低压距离继电器保护范围，同时动作角落入动作区，此时保护发生误动。采用全波傅氏算法，22 ～26.5 ms 时，保护也会发生暂态超越，虽然小于保护启动时间设定值5 ms，但是在极端条件下也可能会发生误动。采用多边形特性半波傅氏算法时，保护超越小矩形动作区10 ms，此时阻抗轨迹落入多边形动作区，保护出现误动。采用全波傅氏算法时也会发生持续7 ms 的超越，保护也会出现误动。

图5 半波傅氏算法出口故障时保护动作特性图

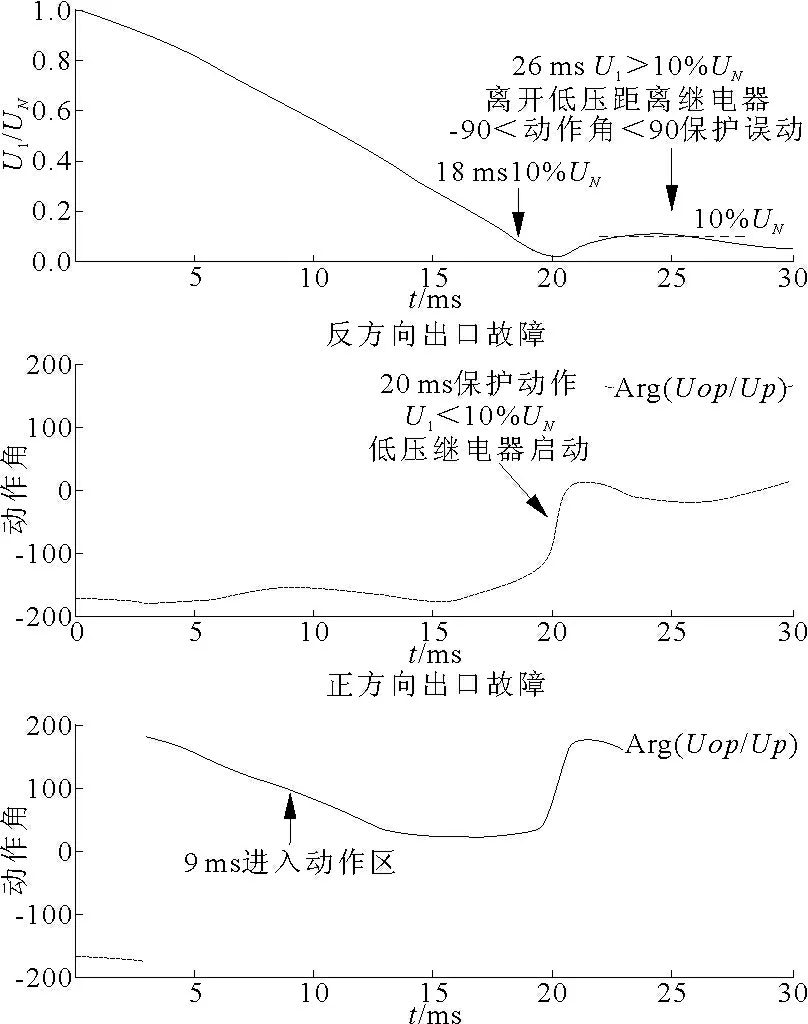
图6 全波傅氏算法出口故障时保护动作特性图

图7 多边形阻抗特性图

(2)正向出口三相短路故障时，在比相欧姆继电器Zk=0 的理想条件下，正序电压U1波形与反方向出口故障时相同。由图5 ～图7 可知，采用半波傅氏算法时，故障后7 ～11 ms 保护进入动作区域，但持续时间小于5 ms，没有达到动作条件，保护不动作;10 ～13 ms 时，U1＜10%UN，时间为3 ms，保护不动作;此后离开门槛值10%UN范围，直到故障后23 ms，重新进入门槛范围，保护才会动作。在此情况下，受CVT 暂态影响，保护动作较慢，使用全波傅氏算法时，故障后9 ms进入动作区，保护可靠动作。使用多边形特性，采用两种算法的阻抗轨迹在故障后7 ms 先进入动作区域，14 ms 后进入小矩形动作区，保护可靠动作。

3.4 防止距离保护超越的方法

受CVT 暂态影响，反向出口故障时，两种保护方法都出现了暂态超越。正向出口故障，半波傅氏算法动作较慢，使用比相欧姆继电器时故障后20 ms 才能动作，严重影响了保护的速动性，而全波傅氏算法基本不会发生超越，动作特性可靠。保护不误动主要依靠低压距离继电器和小矩形动作区，超越主要由电压中的衰减直流分量引起，因此提出以下方法解决暂态超越问题：

(1)提高低压距离继电器启动门槛电压至20%UN或扩大小矩形动作区范围来减少CVT 暂态引起的保护超越。

(2)采用改进半波傅氏算法，消除采样中的衰减直流分量，使保护可靠动作。

3.5 效果分析

图8和图9分别为采用改进半波傅氏算法出口故障时保护动作特性和阻抗特性图。由图8可知，在反方向故障发生后6 ms 保护进入低压距离继电器动作区，由于消除了衰减直流分量，暂态时正序电压幅值低于10%UN，不存在误动可能，保护快速可靠动作。正方向故障后5.25 ms 保护进入动作区，保护可靠动作，同时动作明显快于传统算法;使用多边形特性，正反方向出口故障都不会引起保护的超越，动作特性可靠。

提高门槛电压和扩大小矩形动作区，可以缩小暂态超越的范围，可作为辅助手段配合半波傅氏算法或其他算法使用，使得保护在反方向可靠动作。表1 为采用不同保护方案的动作特性，采用改进傅氏算法配合提高门槛值或扩大小矩形动作区范围的方案时保护动作时间最短且动作特性可靠。

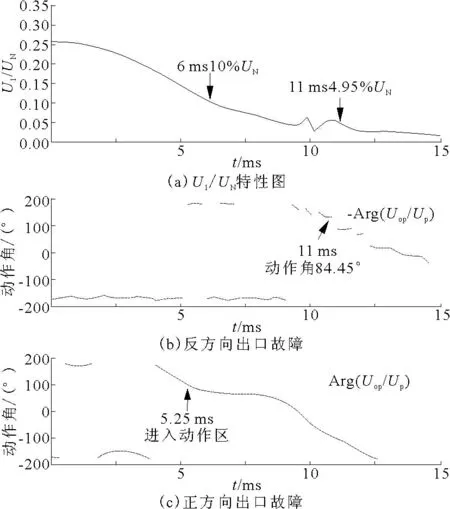
图8 采用改进半波傅氏算法出口故障时保护动作特性图

图9 改进半波傅氏算法多边形阻抗特性图

表1 不同保护方案的动作特性

4 结论

笔者采用PSCAD/EMTDC 建立了220 kV 输电线路模型和CVT 等效模型，分析了输电线路发生故障时CVT 暂态对距离保护的影响，结果表明：

(1)CVT 暂态可以引起两种常用距离保护方案发生超越，其主要原因是反方向故障时，测量数据暂时超越设定门槛值，保护逻辑误判，引起距离保护误动，同时保护算法数据窗长度的不同使得测量精度和灵敏度不能兼顾，可能使保护延迟动作甚至误动。

(2)笔者采用改进半波傅氏算法配合提高低压距离继电器门槛值和扩大小矩形动作区的复合方法，可以消除CVT 暂态引起的保护超越，动作时间短，反应速度快，兼顾可靠性和速动性，保护效果明显提高。

［1］电机工程师手册编写委员会. 电机工程师手册［M］.北京：机械工业出版社，1997：43 -52.

［2］熊小伏，周家启，周永忠，等.电容式电压互感器暂态误差的数字校正方法［J］. 中国电机工程学报，2005(12)：154 -158.

［3］穆淑云.电容式电压互感器暂态性能的仿真计算(续)［J］.电力电容器，2001(2)：1 -8.

［4］HOU D Q，ROBERTS J. Capacitive voltage transformer：transient overreach concerns and solutions for distance relaying［C］∥Canadian Conference on Electrical and Computer Engineering.［S.l.］：［s.n.］，1996：119-125.

［5］施静辉，索南加乐，许庆强，等.电容式电压互感器暂态特性对距离保护影响的研究［J］.西安交通大学学报，2003，37(4)：415 -419.

［6］MARTI J R，LINARES L R，DOMMEL H W. Current trans-formers and coupling -capacitor voltage transformers in realtime simulation［J］. IEEE Transaction on Power Delivery，1997，12(1)：164 -168.

［7］VILLA A，ROMERO Z. Failure analysis of CVT from substations Eltablazo and Cuatricentenario up 400 kV［C］∥Proc 2005 International Conference on Power Systems Transients. Montreal：［s.n.］，2005：143-152.

［8］郁惟镛，吴小建. 电容式电压互感器暂态响应的数字仿真研究［J］.继电器，1998(2)：27 -32.

［9］王黎明，方斌.500 kV 电容式电压互感器暂态特性仿真［J］.高电压技术，2012(9)：2389 -2396.

［10］梅德冬，王文雄，何奔腾，等.电容式电压互感器暂态噪声的研究［J］.继电器，2003(6)：19 -22.

［11］杨奇逊，黄少锋.微型机继电保护基础［M］.北京：中国电力出版社，2013：56 -98.

［12］丁书文，张承学，龚庆武，等. 半波傅氏算法的改进：一种新的微机保护交流采样快速算法［J］. 电力系统自动化，1999(5)：18 -20.

［13］周大敏.一种消除非周期分量对非递推傅氏算法影响的精确方法［J］.继电器，1998(4)：9 -13.

［14］张保会，尹项根.电力系统继电保护［M］.北京：中国电力出版社，2009：76 -107.