基于ICPSO 算法的异步电动机参数辨识与控制
李慧媛,苏义鑫,洪 敏,龙 飞
(1.武汉理工大学 自动化学院,湖北 武汉430070;2. 中国船舶重工集团公司 第七一二研究所,湖北 武汉430064)
矢量控制技术的不断发展和成熟,使得交流电力拖动系统逐步在高性能电力拖动领域占据主导地位。随着人们对控制性能的要求不断提升,异步电动机参数时变性和矢量控制系统对电机参数变化敏感性的问题日益凸显。
对此,国内外专家学者提出了多种异步电动机参数辨识方法。然而,传统的空载与堵转实验辨识法[1],通过施加特定激励辨识法[2],根据电机结构参数辨识[3]等离线辨识方法无法消除电机参数时变带来的影响。最小二乘法[4]、卡尔曼滤波法辨识[5]及模型参考自适应法[6]等经典在线辨识方法因忽略电机的非线性而导致辨识精度不高。自第七届国际自动控制联合会召开以来,诸如神经网络算法[7]、遗传算法[8]和粒子群算法[9]等现代参数辨识算法逐步应用于异步电动机参数辨识中,但这些算法计算量大,且在实时性、收敛性方面难以满足矢量控制系统的要求。
随着研究不断深入,学者们发现单一优化算法难以应对复杂的多参数、非线性动态系统参数辨识问题,于是将目光转向混合优化算法。张益针对粒子群算法容易早熟的问题,提出协同粒子群算法[10];LU 等对免疫粒子群混合算法进行研究[11];刘朝华等首次将人工免疫系统、协同进化思想及粒子群的邻域优势相结合,提出了一种免疫协同粒子群进化模型,并成功应用于永磁同步电机的在线参数辨识[12]。基于这一思想,笔者提出一种免疫协同粒子群优化算法(immune co-evolutionary particle swarm optimization algorithm,ICPSO),应用于异步电动机参数辨识,设计了基于ICPSO 算法的异步电动机矢量控制系统。
1 免疫协同粒子群算法
粒子群算法在解决非线性、不可微、多模态优化问题时具有明显优势,但在计算后期容易失去粒子多样性,出现早熟和进化停滞现象。文献[12]中首次提出了免疫协同粒子群算法,运用协同进化算法的并行计算框架和多个种群间相互作用、共同进化的机制,提升收敛速度,推进粒子群整体的不断演变;同时,利用人工免疫算法的全局搜索优势和超变异能力,提升粒子多样性和大范围搜索能力。算法将整个粒子群体分为优势种群P0与若干普通种群(P1,P2,…,Pn),系统模型如图1 所示。
该算法中,普通种群内部采用混合免疫网络粒子群算法,通过精英粒子保留、免疫网络,以及柯西变异等混合策略共同产生新个体,算法复杂性高,难以适用于异步电动机参数辨识,笔者将其简化,采用标准粒子群算法,利用邻域信息产生新个体。同时,该算法每隔数代运用一次迁移算子,将优势种群的个体返回各普通种群。为提高信息交互针对性,笔者定义进化种群加速度Acc如式(1)所示,以表征普通种群的收敛性变化,进化中每一代都从优势种群中引入若干优良个体,代替收敛性减弱趋势最明显的普通种群中适应度较差的个体。

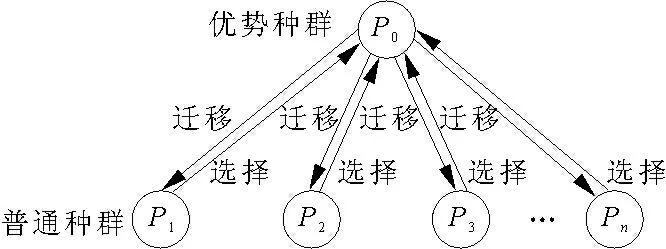
图1 免疫协同粒子群算法的系统模型
式中:Fbesti(k)为第i个普通种群第k代的历史最优适应度;ε 为平滑系数。
所设计的ICPSO 算法进化模式如图2 所示。
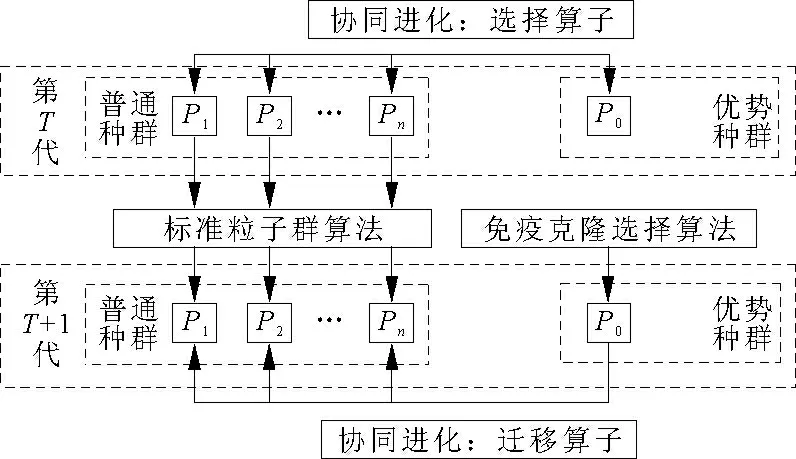
图2 免疫协同粒子群算法的进化模式
算法流程如下:
(1)算法参数初始化,种群初始化。
(2)普通种群内的标准粒子群算法。
(3)协同进化的选择算子,从每一个普通种群中选择一个适应度最高的个体和一个随机个体,构成优势种群。
(4)优势种群内的免疫克隆选择算法。
(5)协同进化的迁移算子,从优势种群中引入若干优良个体,代替收敛性减弱趋势最明显的普通种群中适应度较差的个体。
(6)若符合算法结束条件,则输出结果,算法结束;否则返回到步骤(2)。
2 异步电动机矢量控制系统
2.1 基于ICPSO 算法的异步电动机参数辨识
基于ICPSO 算法的异步电动机参数辨识基本思路是比较异步电动机的输出和可调模型的输出,将两者间差距的函数作为适应性评价标准,运用ICPSO 算法迭代计算,求得满足适应性评价标准的辨识模型参数,基本结构如图3 所示。

图3 基于ICPSO 算法的异步电动机参数辨识结构图
异步电动机在两相静止αβ 坐标系下的状态方程为:
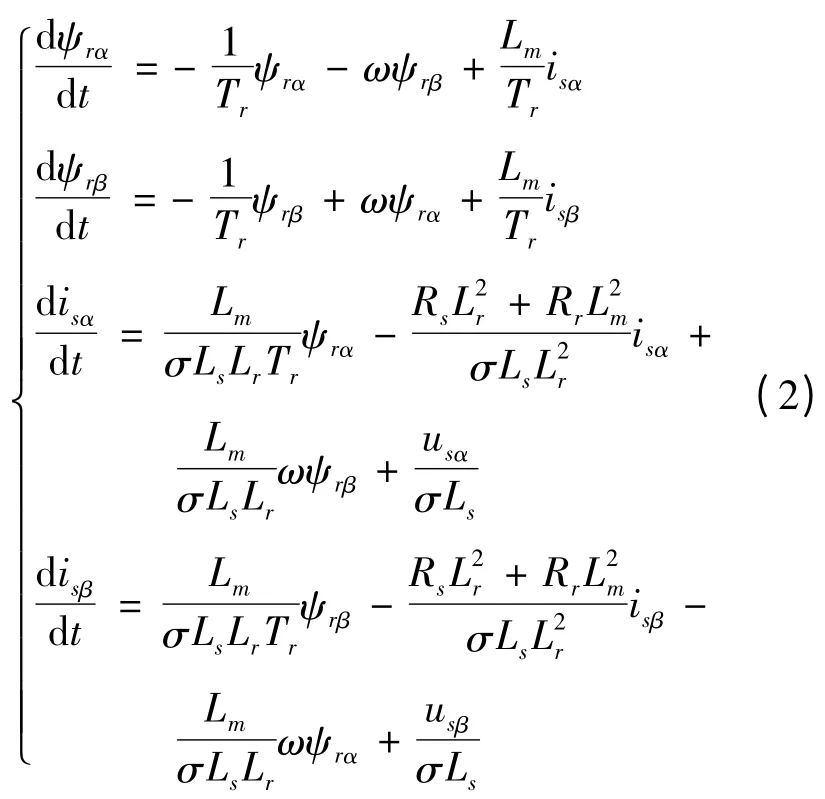
式中:usα,usβ,isα,isβ,ψrα,ψrβ分别为定子电压、定子电流、转子磁链在α、β 坐标轴上的分量;Rs,Rr分别为定子、转子电阻;Ls,Lr,Lm分别为定子、转子自感和互感;转子时间常数Tr =ω 为转子角速度。
确定待辨识的参数为:

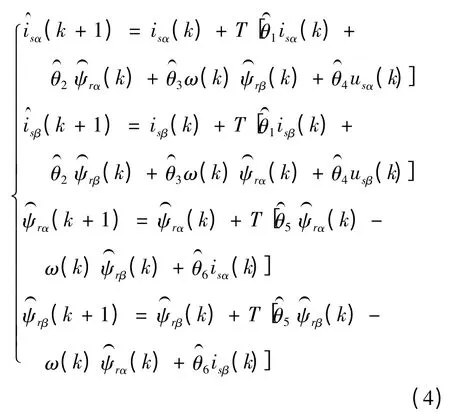

基于ICPSO 算法的异步电动机参数辨识流程如下:
(1)采集实际电机的定子电流值isα(k)、isβ(k),定子电压值usα(k)、usβ(k),以及电机转速ω(k)5 个数据N组。
(3)对每个粒子,计算可调电机模型在各采样时刻的电流估计值
(4)采用ICPSO 算法进行寻优,直至达到迭代次数或寻优结果达到误差许可范围内。
2.2 基于ICPSO 算法的异步电动机矢量控制
在矢量控制系统中,磁链观测器、解耦控制器,以及电流、磁链、转速调节器的参数设定均需运用电机参数,而由于电机参数的时变性,常出现磁链观测不准、控制器参数不合适而影响系统性能。因此,笔者利用ICPSO 算法辨识结果,周期性地对磁链观测器、解耦控制器和PI 调节器进行参数修正。由此,可构建矢量控制系统,如图4 所示。
图4 中ACMR、ACTR、AΨR、ASR 分别是定子电流励磁分量调节器、定子电流转矩分量调节器、转子磁链调节器和转速调节器。
3 仿真实验分析
在Matlab/Simulink 平台上,构建基于ICPSO参数辨识算法的异步电动机矢量控制系统,其中异步电动机模型参数如表1 所示。
设置ICPSO 参数辨识算法参数如表2 所示。
在Simulink 仿真过程中,每运行0.1 s,输出一次pause 指令暂停Simulink 中的模型运行,并依据此前异步电动机模型产生的N组定子电流值isα(k)、isβ(k),定子电压值usα(k)、usβ(k),电机转速ω(k)值,执行一次ICPSO 参数辨识算法,将辨识结果(Rs,Rr,Ls,Lr,Lm,Tr,σ)输出,再通过输出一次continue 指令,启动Simulink 中系统模型的运行,实现在线辨识过程的仿真。
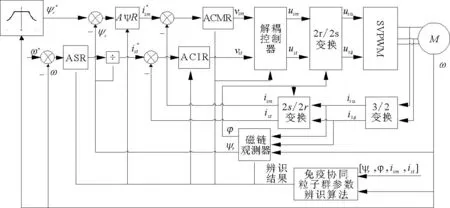
图4 基于ICPSO 参数辨识算法的异步电动机矢量控制系统结构图

表1 异步电动机模型参数

表2 ICPSO 算法主要参数
为了检验ICPSO 参数辨识算法对缓慢变化的电机参数的辨识能力,以转子参数为例,将转子电阻Rr和转子电感Lr的实际值按式(6)和式(7)变化时,参数在线辨识结果能快速响应,跟踪给定值,辨识结果如图5 所示。设转子磁链的给定值为1.2 Wb,电机给定转速为140 rad/s,电动机空载启动,到2 s 时突增负载达20 N·m。观察电机转子磁链曲线、电机转速曲线、电磁转矩曲线分别如图6 ~图8 所示。

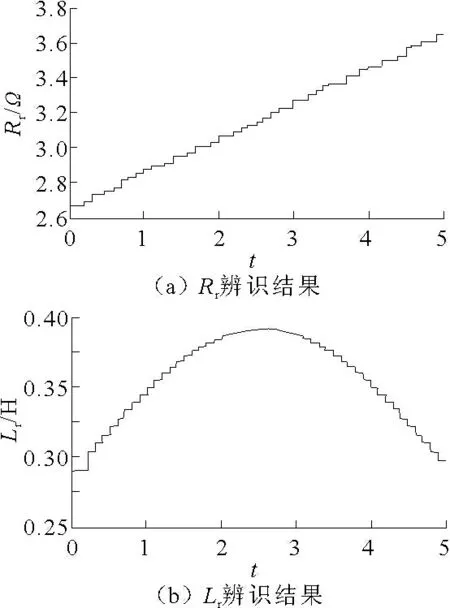
图5 电机参数辨识结果
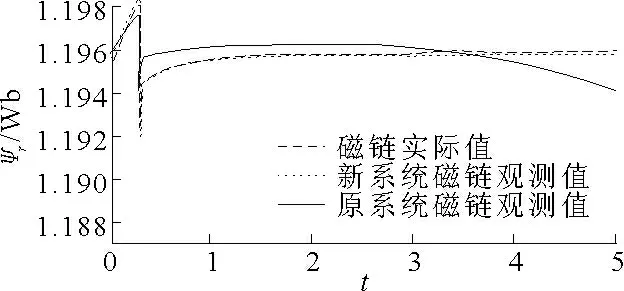
图6 转子磁链局部放大对比曲线

图7 电机转速局部放大对比曲线
由图6 可见,所设计的矢量控制系统在运行时,能迅速建立转子磁链,且基本保持恒定,达到转子磁链与电磁转矩独立控制的要求,较传统系统具有更高的磁链观测精度。由图7 可见,所设计的矢量控制系统在启动时速度响应快,转速跟踪性能良好,且在转速输出的精度上具有更好的表现。由图8 可见,经空载启动和突增负载测试,所设计的矢量控制系统的电磁转矩具有优良的静、动态特性,较传统系统能够抑制电机参数变化对电磁转矩的影响。

图8 电磁转矩曲线
4 结论
笔者将免疫克隆选择算法、协同进化算法和粒子群算法三者相结合,提出了一种免疫协同粒子群优化算法,并将其用于异步电动机参数在线辨识,实时调整解耦控制器、磁链观测器和PI 调节器参数,实现参数自适应,在此基础上设计了基于ICPSO 算法的异步电动机矢量控制系统。经仿真实验验证,ICPSO 参数辨识算法对于异步电动机参数辨识具有有效性;所设计的系统与传统的异步电动机矢量控制系统相比,能够降低电机参数变化的影响,提升磁链观测准确性及转速跟踪性、电磁转矩稳定性,提高控制系统性能。
[1]罗慧,刘军锋,万淑芸. 感应电机参数的离线辨识[J]. 电气传动,2006(8):16 -21.
[2]小林贵彦,金原义彦,李东钰. 感应电机离线参数辨识方法[J]. 电力电子,2009(3):9 -15.
[3]SAKTHIVEL V P,BHUVANESWARI R,SUBRAMANIAN S. Multi -objective parameter estimation of induction motor using particle swarm optimization[J].Engineering Applications of Artificial Intelligence,2010,23(3):302 -312.
[4]MAURIZIO C,MARCELLO P,GIANSALVO C,et al.A new experimental application of least-squares techniques for the estimation of the induction motor parameters[J]. IEEE Transactions on Industry Applications,2003,39(5):1247 -1256.
[5]张猛,肖曦,李永东. 基于扩展卡尔曼滤波器的永磁同步电机转速和磁链观测器[J]. 中国电机工程学报,2007,36(1):36 -40.
[6]陈振锋,钟彦儒,李洁. 嵌入式永磁同步电机自适应在线参数辨识[J]. 电机与控制学报,2010(4):9-13.
[7]RAJ M B,ALEXANDER G P,HAMID A T. Neural speed filtering for sensorless induction motor drives[J].Control Engineering Practice,2004,12(6):687-706.
[8]HUANG K S,KENT W,WU Q H,et al. Parameter identification of an induction machine using genetic algorithms[C]∥Proceedings of the 1999 IEEE International Symposium on Computer Aided Control System Design.[S.l.]:[s.n.],1999:510 -515.
[9]HUYNH D C,DUNNIGAN M W. Parameter estimation of an induction machine using advanced particle swarm optimisation algorithms[J]. IET Electric Power Applications,2010,4(9):748 -760.
[10]张益. 基于协同粒子群算法的PMSM 在线参数辨识[D].武汉:华中科技大学图书馆,2012.
[11]LU H,JI Z C,GONG C L. Study on immune PSO hybrid optimization algorithm[C]∥Chinese Conference on Pattern Recognition. 2009 (CCPR 2009).[S.l.]:[s.n.],2009:1 -4.
[12]刘朝华,章兢,李小花,等.免疫协同微粒群进化算法的永磁同步电机多参数辨识模型方法[J]. 自动化学报,2012,38(10):1698 -1708.

