二阶TGV 结合小波变换模的图像去噪算法

张文静，吴传生，刘 欣

(武汉理工大学 理学院，湖北 武汉430070)

图像去噪是图像处理领域中的一个经典问题，也是图像处理的底层技术之一。图像去噪的目的是根据观察到的降质图像恢复原始真实图像。在实际去噪过程中，一般图像中的噪声是不能够完全去除的，因此很难获得原始不含噪声的图像，而是得到原始不含噪图像的估计图像，也是某种意义下的最优逼近。

图像去噪方法很多，按照处理域的不同，图像去噪方法主要分为两大类：空间域去噪和变换域去噪。空间域方法有均值滤波、中值滤波、非局部平均滤波等;变换域去噪方法有基于傅里叶变换的降噪法和基于小波变换的去噪方法等。基于偏微分方程(partial differential equation，PDE)的图像去噪方法是空间域去噪的一种重要方法。偏微分方程的应用主要分为两类：一种是基于方程的模型，另一种是基于变分法的思想。

在利用变分法去除图像噪声的方法中，经典的模型为RUDIN 等提出的TV 模型［1］。TV 模型克服了许多传统方法的不足，在去除噪声的同时能够较好地保持图像的边缘，且TV 模型具有成熟的解的适定性质及数值解法理论，因此引起了众多学者的广泛关注。但是TV 模型仅能有效地逼近分片常数函数，在去噪时容易造成图像平滑区域的阶梯效应。目前，许多学者针对该问题提出了大量的改进模型，如四阶偏微分方程模型、二阶与四阶偏微分方程相结合的模型、LOT 模型及TV-Stokes 模型等。

2009 年，BREDIES 等提出了总广义变分(total generalized variation，TGV)［2-3］的数学概念。不同于TV，TGV 能够有效逼近任意阶的多项式函数，并且还具有旋转不变性、凸性和下半连续等优良性质。许多理论分析和实验结果都表明，TGV 作为正则项在进行建模时能够较好地防止阶梯效应的产生。

笔者提出了用二阶TGV 正则项代替TV 正则项的图像去噪模型，该模型在去噪的同时能够避免阶梯效应的产生。同时，笔者研究了小波变换的模在边缘检测时的优良性质，引入以小波变换模为参数的边缘检测函数，使新模型能够对图像边缘和细节信息进行更好的保护。

1 TV 与TGV

根据噪声性质的不同，有不同的图像模型。笔者主要考虑加性噪声的情况，因此，图像去噪的数学模型为：

式中：f为观察到的带噪图像;u为原始清晰图像;n为加性噪声。

图像去噪是一个不适定［4］的线性逆问题，不具备解的存在性、唯一性和稳定性的条件。不适定问题一般可通过正则化模型求解。经典的去噪模型为TV 模型，表达形式为：

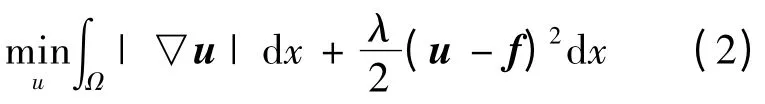
其中：第一项为TV 正则项;第二项为数据保真项;λ≥0 为正则参数;Ω 为一有界区域。

用TV 模型去噪时，会使图像光滑区域产生阶梯效应。BREDIES 等提出了TGV 的数学概念。

设Ω⊂Rd是一个开区域，k≥1 且α0，…，αk-1＞0，则对任意的u∈(Ω)，k阶TGV 定义为：

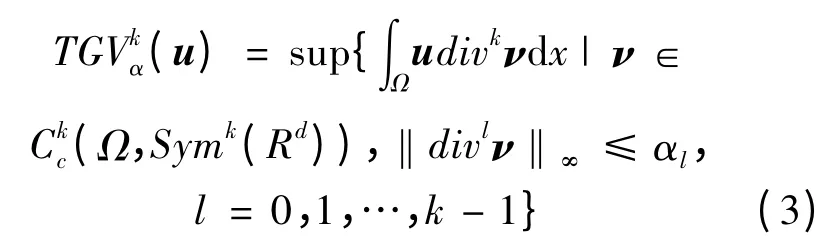
其中，Symk(Rd)为k阶对称张量。

当k=1 且α ＞0 时，有：

因此，TGV 可以看成是TV 的推广。

利用Lengendre-Fenchel 对偶［5］，式(3)可以转换为：

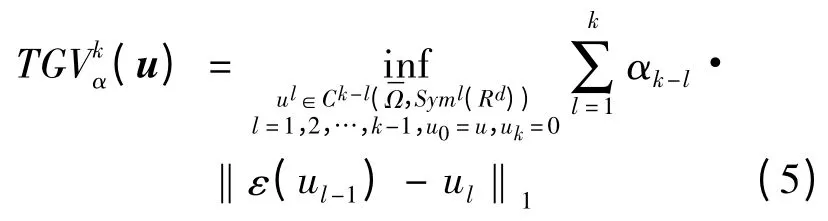
其中，ε(ul-1)为对称梯度算子。

根据式(4)，二阶TGV 可转化为：

其中，BD(Ω)为有界扭曲的向量场空间，满足∀ω∈BD(Ω)，弱对称的导数ε(ω)ω+▽ωT)是一个矩阵值的Radon 度量。

用TGV 正则项代替TV 正则项，得到的图像去噪模型为：

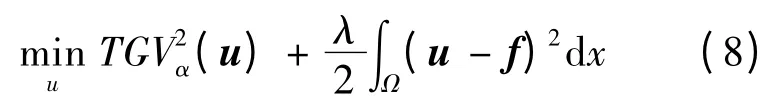
2 小波变换模

图像的边缘通常位于图像灰度变化最大的地方，即图像灰度的突变点。小波变换［6］是图像边缘分析的一种重要方法，其将图像信号在不同尺度下进行分解，信号的突变点(包括噪声点、边缘等)可由小波变换的过零点或极值点以及在不同尺度分量的变化来表示。图像在不同尺度上小波变换的模极大值［7］集合包含了图像中最重要的信息。图像的信号和噪声在不同尺度下的小波变换模特性也不同。对图像进行若干次小波变换，随着尺度的增大，信号和噪声所对应的模极大值会分别增大和减小。因此可利用该性质区别噪声和信号。

设θ(x，y)为二维平滑函数，满足以下条件：

对于任意图像信号f(x，y)∈L2(R2)，(f*θa)(x，y)表示f(x，y)经θa(x，y)平滑后的图像，a为平滑的尺度。

由θa(x，y)定义的两个二维小波为：

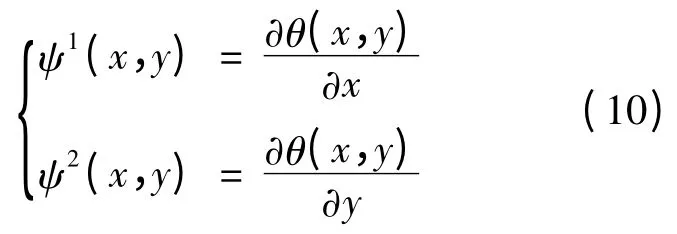
f(x，y)在尺度a上的小波变换的两个分量为：

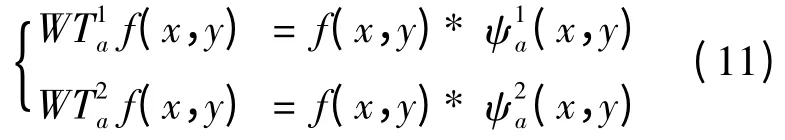
其矢量形式为：

当a为二进制小波变换时，a为2j(j∈Z)。

梯度矢量的模和梯度方向的表达式为：

若梯度模在(x，y)处为极大值，则意味着(f*θa)(x，y)在此处具有最大的方向导数，也就表明f(x，y)在(x，y)处发生突变，且方向为梯度方向，则可以认为(x，y)为图像f(x，y)的边缘点。

3 新模型

通常认为图像上变化剧烈的点为图像的边缘点，由上述分析可知，梯度模为局部极大值的点可认为是图像灰度突变点，即图像的边缘点。为保持图像边缘与细节，笔者考虑把小波变换模作为参数引入到TGV 正则化模型中，得到的新模型为：

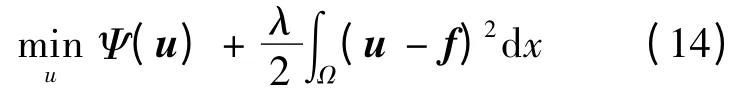
其中：

由上述模型可知，在给定对比因子K的情况下，当|Ma f(x，y)|较大时，即对应为图像的边缘处，边缘检测函数g(Ma f(x，y))的值很小，意味着扩散较小，从而图像的边缘得到了保留。反之，当|Ma f(x，y)|较小时，则对应图像的平坦区域，此时g(Ma f(x，y))的值接近于1，意味着扩散较强，从而能够很好地去除平坦区域的噪声。因此，新模型在去除噪声的同时较好地保持了图像边缘。

利用Legendre -Fenchel 变换［8］，得到模型的对偶形式为：

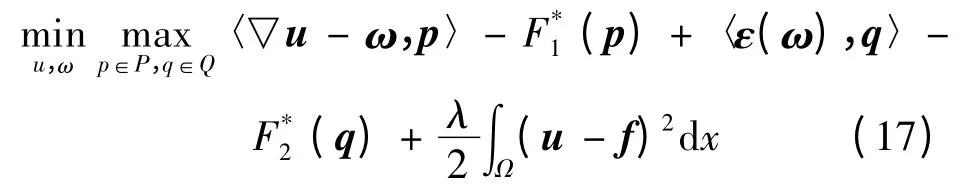
其中：

用原始-对偶算法［9］求解式(17)的迭代公式为：

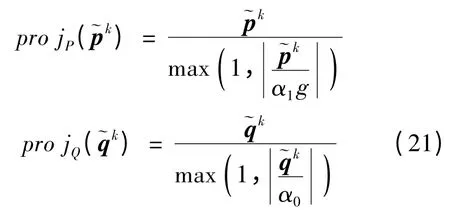
divh为对称梯度算子ε 的复共轭，divh= -ε*，divh(q)

上述模型的数值解法步骤为：

(1)初始化。u0，¯u0=f，ω0，¯ω0=0，p0，q0=0，δ，τ，λ ＞0，k=0;

(3)若uk+1和ωk+1收敛，则终止迭代过程。否则令k=k+1，继续步骤(2)。

4 数值实验

为了克服单纯凭主观视觉判断图像质量的局限性，笔者采用了一些客观算法评价标准［`10］。

设图像的分辨率为M×N，均方误差(mean square error，MSE)为：

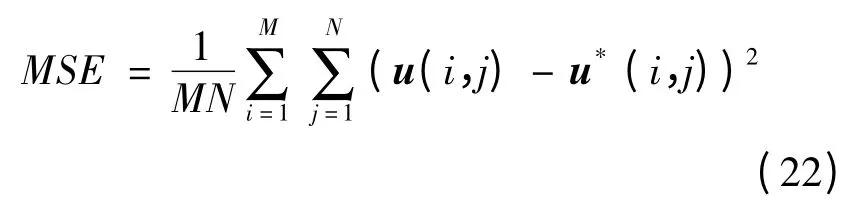
均方误差的值越小，表明去噪后的估计图像与原始图像的近似度越高，去噪效果越好。

峰值信噪比(peak signal to noise ratio，PSNR)为：

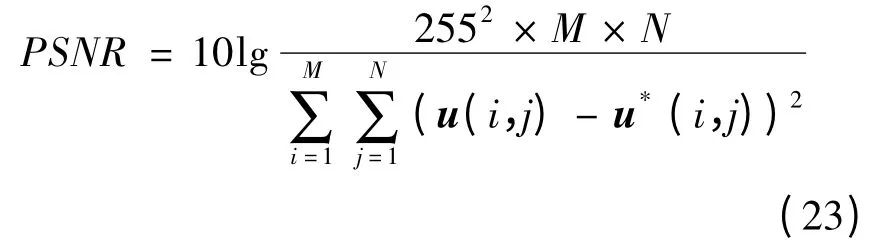
峰值信噪比越大，表示去噪效果越好。

笔者采用Lena 图像作为测试图，TV 模型与新模型的PSNR及MSE结果比较如表1 所示，图1 为实验的结果。

表1 TV 模型与新模型的PSNR 及MSE 结果比较

由实验结果可知，用TV 模型进行去噪后的图像中含有大量的阶梯效应，看起来并不光滑，而新模型去噪后的图像中不存在这种现象，且新模型较好地保持了图像边缘。对上述两种方法峰值信噪比和均方误差的结果进行比较可知，新模型优于TV 模型。

图1 Lena 图实验结果

5 结论

笔者提出了用二阶TGV 正则项代替TV 正则项的图像去噪模型，并在该模型中引入了以小波变换模为参数的边缘检测函数。实验结果和质量评价参数的计算结果表明，该模型能够有效缓解阶梯效应，并能保持良好的边缘。

［1］RUDIN L，OSHER S，FATEMI E.Nonlinear total variation based noise removal algorithms［J］. Physical D，1992(60)：259 -268.

［2］BREDIES K，KUNISCH K，POCK T.Total generalized variation［J］. SIAM Journal on Imaging Sciences，2010，3(3)：492 -526.

［3］BREDIES K，VALKONEN T.Inverse problems with second-order total generalized variation constraints［C］∥Proceedings of Samp TA.［S.l.］：［s.n.］，2011：201-213.

［4］刘继军.不适定问题的正则化方法及应用［M］. 北京：科学出版社，2005：76 -134.

［5］CHAMBOLLE A.An algorithm for total variation minimization and applications［J］.Journal of Mathematical Imaging and Vision，2004，20(1 -2)：89 -97.

［6］孙延奎. 小波变换与图像、图形处理技术［M］. 北京：清华大学出版社，2012：54 -87.

［7］王相海，张洪为，王爽.一种小波变换模极大值的扩散模型［J］.中国图像图形学报，2011，16(6)：1080-1085.

［8］许建楼.交替方向法和TGV 正则在图像处理中的应用研究［D］.西安：西安电子科技大学图书馆，2013.

［9］CHAMBOLLE A，POCK T. A first-order primal-dual algotithm for convex problems with applications to imaging［J］. Journal Mathematical Imaging Vision，2011，40(1)：120 -145.

［10］陈忠.基于贝叶斯理论的图像复原算法研究［D］.武汉：武汉理工大学图书馆，2012.