基于层次分析法的个人购车决策问题
袁朴玉


摘 要:介绍层次分析法的基本原理及应用的基本步骤,并且成功地运用层次分析法解决一个多目标决策问题,证明层次分析法的可行性与实用性。
关键词:层次分析法;多目标决策;个人购车
中图分类号:F224.9 文献标志码:A 文章编号:1673-291X(2015)12-0067-04
引言
层次分析法(The analytic hierarchy process)简称A H P,在20世纪70年代中期由美国运筹学家托马斯·塞蒂(T.L.Saaty)正式提出,它是定性与定量相结合的、系统化、层次化的分析方法。由于它在处理复杂决策问题上的应用性和有效性,很快在世界范围得到重视,它的应用已遍及经济计划和管理、能源政策与分配、行为科学、军事指标、运输、农业、教育与人才、医疗和环境等领域。
一、层次分析法的基本原理
AHP是处理有限个方案的多目标决策问题时常用的方法之一。它是以层次架构来组织决策元素,进而融入专家或实际参与决策者的意见,帮助决策者作出评估判断的思维方法。它的基本思想是把复杂问题分解为若干层次,即把决策问题按总目标、评价标准、具体措施的顺序分解为不同层次结构,最后在低层次通过两两比较得出各因素相对上一层的权重并逐层进行,最后利用加权求和方法综合排序以求出各方案对总目标的权重,权重最大者为最优方案。
二、层次分析法的基本步骤
第一步,建立层次结构模型。在深入分析实际问题的基础上,以图的方式来表示这一问题的总目标,使用标准(或准则)和决策选项,建立层次模型。最高层为目标层,表示解决问题的目的,通常有1个因素;中间层为准则层,表示要实现预定目标所涉及的中间环节;最低层为决策层,表示解决问题的措施或方案。
第二步,构造成对比较矩阵。从层次结构模型第二层开始,对于从属于(或影响)上一层每个因素的同一层诸因素用成对比较法和1~9比较尺度构成成对比较矩阵,用于表示针对上一层某因素而言,本层与之有关的各因素之间的相对重要性。而这里所用的信息基础主要是人们对每一层各因素的相对重要性给出的人工判断。
第三步,层次单排序与一致性检验。根据成对比较矩阵计算对于上一层某因素而言,本层与之有关的因素的重要性次序的权值,即层次单排序。它是本层次所有因素相对上一层而言的重要性进行排序的基础,层次单排序可归结为计算成对比较矩阵的特征值和特征向量。由于成对比较的数量比较多,很难做到完全一致。事实上,任何成对比较矩阵都允许存在一定程度上的不一致。为了解决一致性问题,AHP提供了用一致性指标CR来测量决策者做成对比较的一致性。若CR>0.10,则表明成对比较存在不一致;若CR≤0.10,则表明成对比较的一致性设计较合理,可以继续A H P的以下步骤。
第四步,层次总排序。利用同一层次中所有层次单排序的结果计算针对上一层而言本层所有因素重要性的权值,即层次总排序。由于总排序过程是从最高层到最低层逐层进行的,而最高层为总目标,所有层次总排序也是计算某一层次各因素相对于最高层的相对重要性的排序权值。
三、实例研究——用A H P方法解决个人购车问题
决策者在对几部车的样式和配件初步分析后,选择了三种车型:速腾1.6L领先型,雪铁龙1.6L时尚型,朗动1.6L领先型,下页表1总结了决策者搜集的关于这些车的信息,并且认为选车的决策与下列标准有关:(1)价格;(2)油耗;(3)舒适性;(4)样式。
(一)建立层次结构模型
(二)构造成对比较矩阵
A H P具有的灵活性能够反映每个决策者的独特偏好,考虑的标准随着决策者变动。为了衡量各个标准之间的相对重要性,A H P采用分值1~9来测量。在4个标准构成的成对比较矩阵中,用1、3、5、7、9分别对应“一般重要”、“较重要”、“很重要”、“非常重要”、“极重要”,而居中的评价比如重要的程度在“非常重要与很重要之间”则对应6分。在每个标准下三种车型构成的成对比较矩阵中,用1、3、5、7、9分别对应“一般喜爱”、“较喜爱”、“很喜爱”、“非常喜爱”、“极喜爱”,用于表示对某种车的偏爱程度。
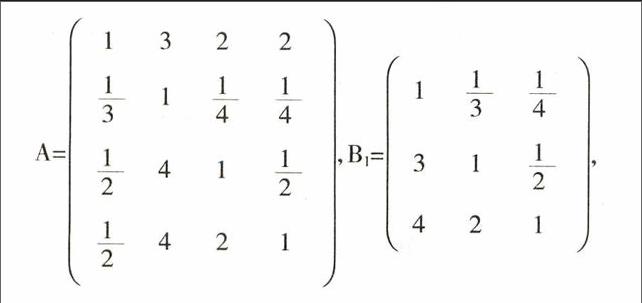
4个标准构成的成对比较矩阵记作A,在价格标准下三种车型构成的成对比较矩阵记作B1,在油耗标准下三种车型构成的成对比较矩阵记作B2,在舒适性标准下三种车型构成的成对比较矩阵记作B3,在样式标准下三种车型构成的成对比较矩阵记作B4。则:
A=,B1=,
B2=,B3=,
B4=
在矩阵中A,第一行第二列的“3”,表示价格与油耗相比,价格更重要一点。同理,在矩阵中B3,第一行第三列的“8”,表示在舒适性标准下决策者对速腾比对朗动的偏爱程度在强烈与极强烈之间。
(三)层次单排序与一致性检验
1.各标准的优先排序与一致性检验
各标准优先排序的计算步骤:先计算每列值的总和;接着矩阵的每一项都除以它所在列的总和;最后求每行的平均值即为每个标准的优先级。
各标准的一致性指标的计算步骤:先将成对比较矩阵中第一列的每一项都乘以第一项标准的优先级,第二列的每一项都乘以第二项标准的优先级,以此类推,完成成对比较矩阵的竖列;然后计算每行的总和,得到一向量“加权值”;接下来,将得到的加权值对应除以每个标准的优先级,得到4个数值;再计算上步得到的数值的平均值,记为λmax;接着计算一致性指数CI,CI;最后计算一致性指标CR,CR=,其中RI是任意一个成对比较矩阵的一致性指标,其值取决于该比较的项目个数,当n=3时,RI=0.58;当n=4时,RI=0.90。
如前所述,4个标准构成的成对比较矩阵的一致性程度达到要求,可以得出结论:这个成对比较的一致性是可以接受的。
2.各标准下三种车型的优先排序与一致性检验
由上述相关计算的详细步骤列表表示其相应结果。表4表示各标准下三种车型的优先排序,表5 表示对成对比较矩阵所做的一致性检验的结果。
由表4可以看出,按价格标准朗动(0.557)是最佳选择;按油耗标准朗动(0.639)也是最佳选择;按舒适性标准速腾(0.593)是最佳选择;按样式标准雪铁龙(0.656)是最佳选择。
由表5得出,这些成对比较的一致性都达到要求,所以结论是可以接受的。
(四)层次总排序
层次总排序的计算过程为将每部车的优先级乘以对应标准的优先级,累计总和即可。
速腾的层次总排序:
0.398×0.123+0.085×0.087+0.218×0.593+0.299×0.265=0.265
雪铁龙的层次总排序0.398×0.320+0.085×0.274+0.218×0.341+0.299×0.656=0.421
朗动的层次总排序:
0.398×0.557+0.085×0.639+0.218×0.065+0.299×0.080=0.314
排列上述优先级,可得决策选项的A H P排名:(1)雪铁龙,(2)朗动,(3)速腾。以上结果为决策者提供了依据,也帮助决策者更好地理解在决策过程中的利益权衡,同时也更清晰地理解为什么A H P推荐雪铁龙的原因。
结语
层次分析法作为一种有用的决策工具,具有明显的优点,如实用性、简洁性和系统性。正如许多正在发展的理论和方法一样,层次分析法在应用上也具有一定的局限性。首先,层次分析法得出的结果是粗略地安排次序,不适用于有较高定量要求的决策问题;其次,其结论是建立在成对比较矩阵是一致性矩阵的基础上的。而在实际应用中由于各方面原因往往得不到具有一致性的成对比较矩阵,而需要对其进行一致性检验,并进行修改,因此成对比较矩阵的建立过程比较复杂,并且存在较大的主观性。故应用时应注意:(1)分解简化问题时把握住主要因素,不漏不多;(2)注意相比较元素之间的强度关系,相差太悬殊的要素不能在同一层次比较。

