子空间格代数上的局部Lie导子

王 婷，徐国东，常彦妮

（南阳师范学院数学与统计学院，河南 南阳 473061）

子空间格代数上的局部Lie导子

王 婷＊，徐国东，常彦妮

（南阳师范学院数学与统计学院，河南 南阳 473061）

研究子空间格代数Alg 上的局部Lie导子，其中 是Banach空间X上子空间格且（0）＋＝∧｛M∈ ：M⊈（0）｝≠（0）.利用子空间格代数Alg 上Lie导子的已有结构，证明了如果δ：Alg →B（X）是局部Lie导子，则存在两线性映射T：X＊→X＊，S：）＋＋→X＊＊，使得对任意x∈（0）＋，f∈X＊有，其中（）＋是（0）＋在X＊＊中的典型映射像.

Lie导子；局部Lie导子；幂等算子

局部导子的概念最早由 Kadison［1］和 Larson等［2］分别独立引入.Kadison［1］496证明了从von Neumann代数到它的任意对偶双边模关于范数连续的局部导子必为导子，而Larson等［2］189得到了Banach空间X上全体有界线性算子B（X）代数上的局部导子是导子.除了探讨与结合积有关的导子［3］外，研究与Lie积有关的Lie导子也是一个热点，而刻画某些代数上Lie导子的结构是Lie导子的经典问题.近年来，这类问题主要在 J－子空间格代数［4］、von Neumann代数［5］、三角代数［6－7］及B（X）代数［8］上进行探讨.受局部导子的启发，Chen等［9］引入了局部Lie导子的概念，刻画了B（X）代数上局部Lie导子的结构；随后，又研究了套代数上局部Lie导子的结构［10］.目前，有关局部Lie导子刻画的研究还不多，本文主要借助已有算子代数上Lie导子的结构，进一步探讨一类特殊子空间格代数上局部Lie导子的性质.

1 预备知识

设X是数域F上的Banach空间，这里F是实数域或复数域，X＊表示X的（拓扑）对偶空间，B（X）表示X上全体有界线性算子，I表示X上的恒等算子.对任意A，B∈B（X），称［A，B］ABBA为B（X）中的交换子［11］.X上的子空间格 是X的一个包含零空间（0）和X的闭子空间链，且该闭子空间链对任意交和任意闭封闭.设 是子空间格，定义

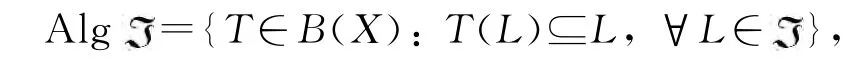
其中∨表示子空间的闭线性扩张，∧表示闭子空间的交.

定义1［4］53设δ为代数 到其自身的线性映射，若∀A，B∈ ，有δ（AB）＝δ（A）B＋Aδ（B），则称δ为导子；若∀A，B∈ ，有δ［A，B］＝［δ（A），B］＋［A，δ（B）］，则称δ为Lie导子.

定义2［1］494设δ为代数 到其自身的线性映射，若∀A∈ ，存在导子δA使得δ（A）＝δA（A），则称δ为局部导子.

定义3［9］110设δ是从代数 到其自身的线性映射，若∀A∈ ，存在Lie导子δA使得δ（A）＝δA（A），则称δ为局部Lie导子.

引理1［12］设X是维数大于2的Banach空间， 是X上的子空间格且（0）＋≠（0）.若δ：Alg →B（X）是Lie导子，则存在算子T∈B（X＊）和可将交换子映为零的线性映射τ：Alg →FI，使得∀A∈Alg ，有δ（A）＊＝［A＊，T］＋τ（A）.

引理2［11］329设X是Banach空间，A，B∈B（X），λ∈F.若［A，B］＝λI，则λ＝0.

引理3［12］262设X是Banach空间，M，N分别是X，X＊的非零子空间，φ：M×N→B（X）是一个双线性映射.如果对任意x∈M，f∈N，有φ（x，f）ker（f）⊆Fx，则存在两个线性映射T：M→X，S：N→X＊，使得φ（x，f）＝Tx⊗f＋x⊗Sf.

2 主要结果

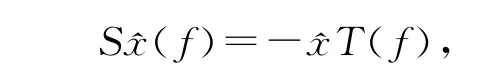
证明 设x→是从X到X＊＊的典型映射.对任意x∈X，可确定X＊中的一个典型映射φx，使得φx（x）＝1，于是X＊＝Fφx⊕ker（）.由δ：Alg →B（X）是局部Lie导子，得到对任意A∈Alg ，存在Lie导子δA：Alg →B（X），使得δ（A）＝δA（A）.再由引理1知存在算子TA∈B（X＊）和可将交换子映为零的线性映射τA：Alg →FI，使得δ（A）＊＝［A＊，T A］＋τA（A）.设x∈（0）＋，f∈X＊，令A＝x⊗f，则

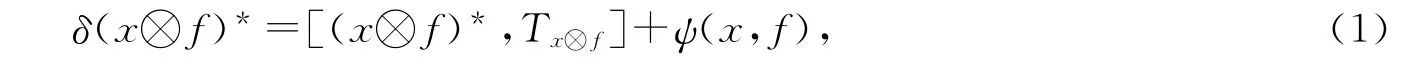
式中ψ（x，f）＝τx⊗f（x⊗f）.

下证ψ（x，f）是双线性的.首先证明ψ是齐次的.设x∈（0）＋，f∈X＊，λ∈F，则由（1）式得

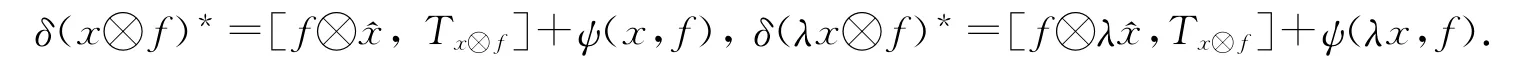
比较两式并注意到δ（λx⊗f）＊＝λδ（x⊗f）＊，于是ψ（λx，f）－λψ（x，f）＝［λf⊗，T x⊗f－Tλx⊗f］.因ψ（λx，f）－λψ（x，f）∈FI，故由引理2有ψ（λx，f）－λψ（x，f）＝0，这说明ψ关于第一个变量是齐次的.类似可证ψ关于第二个变量也是齐次的.

其次证明ψ（x，f）关于两个变量是可加的.为此，断言对任意x∈（0）＋，f∈X＊，若（f）＝0，则有ψ（x，f）＝0.事实上，取g∈X＊使得（g）＝1，则f⊗＝［f⊗，g⊗］，即f⊗是交换子，从而ψ（x，f）＝τx⊗f（x⊗f）＝0.设x1，x2∈（0）＋，f∈X＊，若，则ψ（x1＋x2，f）＝ψ（x1，f）＝ψ（x2，f）＝0，于是ψ（x1＋x2，f）＝ψ（x1，f）＋ψ（x2，f）；若，则取g∈且与f线性无关.由（1）式可知，存在λ，λ1λ2∈F使得δ（x1⊗f）＊g＝ψ（x1，f）g＋λ1f，δ（x2⊗f）＊g＝ψ（x2，f）g＋λ2f，δ（（x1＋x2）⊗f）＊g＝ψ（x1＋x2，f）g＋λf.比较这些等式并注意到δ（（x1＋x2）⊗f）＝δ（x1⊗f）＋δ（x2⊗f），得

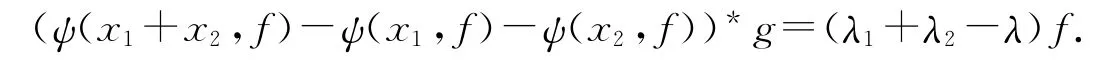
因g与f线性无关，ψ（x1＋x2，f）－ψ（x1，f）－ψ（x2，f）＝0，故ψ关于第一个变量是可加的.

为证ψ关于第二个变量是可加的，设x∈（0）＋，f1，f2∈X＊.若f1，f2∈ker（），则

于是ψ（x，f1＋f2）＝ψ（x，f1）＋ψ（x，f2）；若f1，f2不全在ker（）中，则span｛f1，f2｝∩ker（）至多是一维的；从而，取g∈ker（）使得g∉span｛f1，f2｝.再由（1）式可知，存在μ，μ1μ2∈F使得δ（x⊗f1）＊g＝ψ（x，f1）g＋μ1f1，δ（x⊗f2）＊g＝ψ（x，f2）g＋μ2f2，δ（x⊗（f1＋f2））＊g＝ψ（x，f1＋f2）g＋μ（f1＋f2）.比较这些等式并注意到δ（x⊗（f1＋f2））＝δ（x⊗f1）＋δ（x⊗f2），得

因g∉span｛f1，f2｝，ψ（x1＋x2，f）－ψ（x1，f）－ψ（x2，f）＝0，故ψ关于第二个变量是可加的.

［1］KADISON R V.Local derivations［J］.J Algebra，1990，130（2）：494－509.

［2］LARSON D R，SOUROUR A R.Local derivations and local automorphisms of B（X）［M］／／Operator theory：operator algebras and applications，Part 2（Durham，NH）.Providence，RI：Amer Math Soc，1990：187－194.

［3］李俊，陈琳.一类CSL代数上的完全有界上同调群 ［J］.扬州大学学报（自然科学版），2015，18（3）：16－19.

［4］QI Xiaofei.Characterization of（generalized）Lie derivations on J－subspace lattice algebras by local action［J］.Aequationes Math，2014，87（1／2）：53－69.

［5］BAI Zhaofang，DU Shuanping.The structure of nonlinear Lie derivation on von Neumann algebras［J］.Linear Algebra Appl，2012，436（7）：2701－2708.

［6］BENKOVI D，EREMITA D.Multiplicative Lien－derivations of triangular rings［J］.Linear Algebra Appl，2012，436（11）：4223－4240.

［7］JI Peisheng，QI Weiqing.Characterizations of Lie derivations of triangular algebras［J］.Linear Algebra Appl，2011，435（5）：1137－1146.

［8］LU Fangyan，JING Wu.Characterizations of Lie derivations ofB（X）［J］.Linear Algebra Appl，2010，432（1）：89－99.

［9］CHEN Lin，LU Fangyan，WANG Ting.Local and 2－local Lie derivations of operator algebras on Banach spaces［J］.Int Equat Oper Theory，2013，77（1）：109－121.

［10］CHEN Lin，LU Fangyan.Local Lie derivations of nest algebras［J］.Linear Algebra Appl，2015，475：62－72.

［11］HALMOS P R.A Hilbert space problem book［M］.2nd ed.New York－Berlin：Springer－Verlag，1982：320－331.

［12］LU Fangyan，LIU Benhong.Lie derivations of reflexive algebras［J］.Int Equat Oper Theory，2009，64（2）：261－271.

Local Lie derivations on subspace lattice algebras

WANG Ting＊，XU Guodong，CHANG Yanni

（Sch of Math ＆Stat，Nanyang Norm Univ，Nanyang 473061，China）

Lie derivation；local Lie derivation；idempotent operator

O 177.2

A

1007－824X（2015）04－0041－03

2014－05－31.＊ 联系人，E－mail：tingwang526＠126.com.

国家自然科学基金资助项目（41306207）；国家自然科学基金数学天元基金资助项目（11426140）.

王婷，徐国东，常彦妮.子空间格代数上的局部Lie导子 ［J］.扬州大学学报（自然科学版），2015，18（4）：41－43.

（责任编辑 青 禾）