基于精英保留策略遗传算法的 配电网无功优化

刘 健 李京航 柏小丽

（1.西华大学，成都 610039；2.国网泸州供电公司 四川 泸州 646000）

随着我国经济的迅速发展，用电量逐年增加，客户对电能质量的要求也越来越高[1]。配电网作为电网与用户的直接媒介，其运行质量的好坏直接关系到用户的电能质量的优劣。但在配电网中存在大量的网损，导致节点电压沿馈线下降，致使配电网线路中后段电压幅值低于规定值。另一方面，配电网中存在的感性负荷从系统吸收无功功率，线路上出现大量无功潮流，导致网损增加与电压下降。从电路知识可知，无功功率决定了电压幅值。因此，若要提高电压幅值，满足用电客户对无功和电压需求，需对配电网进行无功补偿。

并联电容器作为一种高效的容性无功补偿方式，以其投资小，运行维护方便，补偿效率高而得到了广泛的应用[2]。无功补偿采取就地平衡原则，电力公司据此原则在配电网负荷中心或电压较低、无功不足的节点安装无功补偿装置，能直接改善补偿点的电压水平，降低有功损耗，但这种未经优化计算的无功补偿通常不能使全网损耗降到最低水平。

配电网无功优化是一个典型的多变量多约束的混合非线性规划问题[3]，这类问题的求解主要有非线性数学方法和现代智能优化算法。现代智能优化算法以其不需要函数的连续性，可导性以及寻优能力强在无功优化问题上得到了广泛的研究和应用[4-6]。简单遗传算法（GA）作为典型的智能优化算法，具有寻优能力强，处理离散变量能力等特性，适合于处理配电网无功优化问题。但随着电力系统规模的扩大，采用GA 计算不仅收敛速度慢，且容易陷入局部最优。

本文在充分考虑配电网运行特性的基础上，考虑到传统GA 存在的问题，对GA 进行改进，采用整数编码精英保留遗传算法（ESGA）对配电网进行无功优化补偿[7]。通过对IEEE33 节点配电系统进行仿真计算，结果表明，所采用的方法能有效降低网损，提高电压水平。

1 无功优化数学模型

配电网无功优化问题通常从经济性和安全性两方考虑建立目标函数。本文以有功网损最小为目标，兼顾系统电压质量，将节点电压偏差作为惩罚函数，建立网损与电压偏差之和最小的目标函数。

式中，有功网损通过潮流计算可得，其计算公式：

NB表示所有的支路，λ为电压越界惩罚因子，N为配电网节点数，Vimax,Vimin为节点电压幅值及其上下限。

无功优化需满足的等式约束为潮流方程：

Pi，Q i为节点i的注入有功和无功功率，V i，Vj，Gij，Bij，δij分别为节点i，j电压，节点i、j之间的电导，电纳，相角差。

满足不等式约束包括控制变量约束与状态变量约束。

控制变量约束：

状态变量约束：

QCimax，QCimin为补偿容电容器QCi的上下限值。

无功优化即是在满足式（4）至式（6）约束的前提下求最小的F值。

2 精英保留遗传算法的基本原理和无功优化步骤

GA 是由霍兰德（Holland）于1975年在他的著作“Adaptation in Natural and Articial Systems”中首次提出来的，是一种借鉴生物界自然选择和遗传机制的高度并行、随机、自适应的搜索方法。鉴于GA在处理离散变量寻优搜索中的优势，GA 在无功优化问题上得到广泛的应用。GA 的基本原理为：通过随机方式产生若干个所求解问题的初始解，即染色体，形成初始种群；通过适应度函数对每个个体进行评价，淘汰适应度值低的个体，选择高适应度的个体参加遗传操作，经过遗传操作后的个体集合形成下一代新的种群，对这个新种群进行下一轮进化。但在进化过程中，当前群体中适应度好的个体可能被破坏。

2.1 编码方式

传统遗传算法的编码方式主要是二进制编码和实数编码。采用二进制编码操作直观，适合处理最优化问题决策变量为离散型的情况。但在连续型问题中易引起精度矛盾和效率矛盾，如果变量的数值比较大，编码会比较长，从而影响计算速度。而采用实数编码，不仅计算速度和精度得到提高，特别是在搜索空间较大时更为明显[8]。本文所选用的是十进制编码，即将电容器的组数用整数编码表示，初始种群的每个个体都是在并联电容器实际的可调范围内随机产生。

2.2 适应度函数

遗传算法在寻优过程中利用适应度值进行搜索，因此适应度函数的选取直接影响到遗传算法能否找到最优解。本文求的目标函数是求最小值，将其转换成求最大值，取目标函数的倒数。

2.3 精英保留策略

遗传算法寻优的过程是种群进化的过程，个体的优劣程度用适应度值表示，适应度值越大，表示个体越优。本文中，定义每一代种群中适应度值最大的个体为精英个体。传统遗传算法的在遗传操作中进行随机选择，交叉，变异操作，并没有将精英个体进行保留。这就有可能导致最优个体的丢失或者找到最优个体的时间延长。本文采用精英保留策略，在遗传操作进行前，将当前种群中的精英个体保留，不参与遗传操作，然后进行选择，交叉，变异产生新一代种群。

在本文中，选择操作采用的方法是随机产生与种群个体数目n等个数的（0，1）之间的小数，将其存储在矩阵中，然后比较每个元素与交叉率的大小关系，找出所有比交叉率小的元素所对应的位置，从当前种群中对应位置提取出个体，组成父代种群。然后在此种群中随机两两选择个体作为父本，交叉产生子代种群。因为本文采用十进制编码，基因个数仅为3，因此只需要进行单点交叉。具体做法是随机产生［1，3］的整数，对每一组父代进行一次交叉点的生成，进行交叉工作。直到进行n/2 次，产生出n个子代，得到新的种群为止。然后对交叉产生的子代进行变异。具体做法是随机产生n个小数组成一个n行1 列的矩阵，再找出小于交叉率的位置对应的个体，对这些个体进行变异操作。变异时随机产生［1，3］的整数，即找到变异点，对变异点的基因赋予新的值，即在其规定的范围内重新随机产生与原基因值不等的基因，对所有选出来的个体完成变异后就产生了新一代的种群。再对新一代个体进行适应度评价，找出其中精英个体与适应度最差的个体。如果保留的精英个体适应度低于子代精英个体，则表示种群已经进化，否则，将子代适应度值最大的个体去替换之前保留的精英个体，同时，之前的精英个体用以替换子代最差个体[9]。

2.4 基于ESGA 的无功优化步骤

1）读入原始网络参数并初始化。

2）计算初始潮流。计算优化前配电网络的潮流，网损，节点电压。

3）产生初始种群。在编码规定的范围之内随机产生包含n个体初始种群X。

4）解码并映射到初始网络进行参数修正。将个体中的编码值解码成为电容值，并以此修正网络参数。

5）精英个体保留。在计算潮流的基础上进行个体适应度评价，并将适应度最好的精英个体保留。

6）遗传操作产生新一代种群。对父代个体进行选择，交叉，变异，产生子代种群并计算其适应度值。

7）若子代种群中的最优个体适应度值比保留的父代好，证明种群已进化，用保留的精英个体替换子代最差个体，同时将精英个体替换为子代最佳个体。

8）若遗传代数大于最大进化代数，终止迭代，结束循环，输出精英个体及对应的优化结果；否则，返回5）。

3 算例结果与分析

在Windows7 计算机上采用Matlab 语言编程对IEEE33 节点配电系统进行了无功优化计算。该系统为辐射状网络，含33 个节点，32 条支路，总负荷3715+j*2300 kVA，基准电压为12.66kV，基准功率100MVA。接线图如图1所示。

图1 IEEE33 节点配电系统接线图

参数设置：最大进化次数100 次，种群数目为30，交叉概率0.8，变异概率0.15，电压允许偏差为系统额定电压的±7%[10]，电压越界惩罚系数取1000，补偿点选择12，23，29 节点[11]。采用前推回代潮流算法，收敛精度为10-5。优化结果见表1，优化前后网损见表2，电压幅值对比如图2所示。

表1 IEEE33 节点配电系统无功优化结果

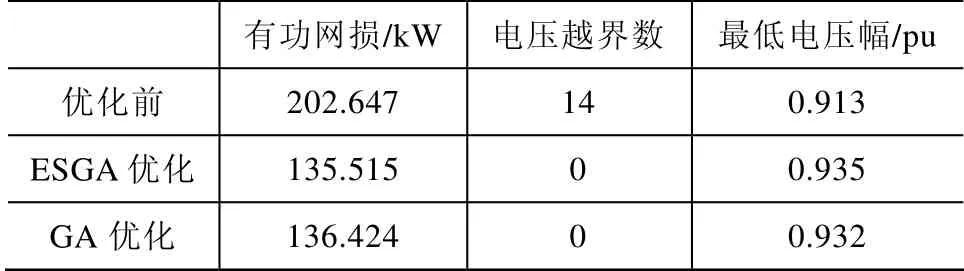
表2 IEEE33 节点系统无功补偿前后比较

从优化结果可看出，通过对该系统3 个节点共补偿2000kVA 的补偿电容，从表2可以看出，ESGA的优化效果好于 GA 优化效果。系统网损从202.647kW 降至135.515kW，降幅为33%。算例中给定的总负荷为该系统的负荷容量，即可视为最大的负荷水平下的负荷。因此，如果以参考电价 0.5 元/kW·h 计算，该系统在进行无功优化配置后，一年最多能节约294038 元。优化后的电压合格率为100%。系统最低电压由0.913pu 提高为0.935pu。仿真结果表明，通过优化补偿，可大幅度降低网损，提高电压水平。

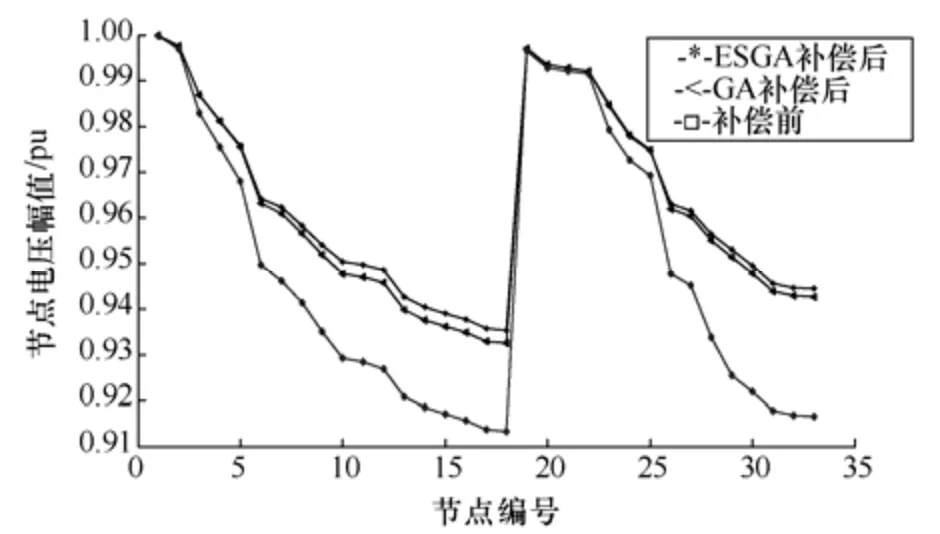
图2 优化前后电压幅值对比

4 结论

本文结合无功优化模型的特点，考虑经济性和电能质量建立了无功优化数学模型。用精英保留策略对传统遗传算法进行改进对所建模型求解。充分考虑并联电容器分组投切的实际情况，按电容器组可调范围进行整数编码求解，减少了算法的随机性，增强了全局寻优能力。算例结果分析表明，采用该方法不仅能有效降低网损，还能提高系统电压质量，可为实际系统的无功优化配置提供一定参考，具有一定的实用价值。

[1] 焦明明,杨仁刚,牛焕娜.配电网高低压综合电压/ 无功优化方法[J].电力系统保护与控制,2010,38(24): 137-141,177.

[2] 王凌谊,候世英,吕厚余,等.电力系统无功优化与无功补偿[J].电气应用,2006,25(10): 96-99.

[3] 赵昆,耿光飞.基于改进遗传算法的配电网无功优化[J].电力系统保护与控制,2011,39(5): 57-62,68.

[4] 刘科研,盛万兴,李运华.基于改进遗传模拟退火算法的无功优化[J].电网技术,2007,31(3): 13-18.

[5] 刘科研,盛万兴,李运华.基于改进免疫遗传算法的无功优化[J].电网技术,2007,31(13): 11-16.

[6] 姚李孝,肖靓,王磊,等.基于改进遗传算法的配电网无功优化[J].电网与清洁能源,2009,25(4): 24-28.

[7] De Jong K A.An analysis of the behavior of a class of genetic adaptive systems[D].University of Michigan.

[8] 双喜、蔡虎、吕佳丽.应用于无功优化的遗传算法的编码问题[J].全国高校电自专业第十四届学术年会论文集,1998.

[9] 张华,郝建奇.基于改进遗传算法的配电网无功优化[J].电气技术,2012,13(6): 28-31,68.

[10] 方向晖.中低压配电网规划与设计基础[M].北京: 中国水利水电出版社,2004.

[11] Haque M H.Capacitor placement in radial distribution systems for loss reduction[J].IEEE Proc.-gener.DIstrib,1999,146(5): 501-505.