基于观测器的不确定非线性系统L1自适应控制
齐晓慧,甄红涛,董海瑞
(军械工程学院无人机工程系,河北石家庄050003)
基于观测器的不确定非线性系统L1自适应控制
齐晓慧,甄红涛,董海瑞
(军械工程学院无人机工程系,河北石家庄050003)
针对一类严格块反馈型不确定非线性系统,采用反步设计方法提出了一种新的基于滑模状态观测器的L1自适应控制方案。由于系统状态不完全可测,首先设计滑模观测器对系统状态进行估计,并分析观测器的收敛性,在此基础上,通过反步法得到系统的理想控制律。为了消除反步控制中的“项数膨胀”,引入非线性跟踪微分器来提取理想控制律的微分信号。为提高系统响应的瞬态性能,消除控制输入的高频振荡,引入L1自适应控制对控制律进行改进,通过理论推导证明了闭环系统的稳定性。最后通过数值仿真算例验证了所设计控制方案具有快速的收敛性、良好的跟踪性等期望性能。
非线性系统;滑模观测器;L1自适应控制;反步控制
0 引 言
在现代控制领域中,随着被控对象越来越复杂,多输入多输出(multiple input multiple output,MIMO)不确定非线性系统的控制问题得到了广泛关注[1-3]。文献[4]针对一类含有未知控制增益矩阵和输入非线性的系统设计了一种变结构自适应控制方案,保证了闭环系统的全局一致有界。文献[5]针对一类含有非线性不确定性的MIMO系统设计了一种L1自适应控制方案,保证了系统的瞬态响应和控制输入的有界性。严格块反馈动态系统是一类常见的非线性系统,现实中很多被控对象都可以转化成此种形式,已有许多学者对此类系统的控制进行了研究[6-8]。文献[9]针对有翼导弹的飞行控制问题,设计了一种带有自适应参数近似的块控反步飞行控制器。文献[10]针对一类含有输入约束的不确定非线性系统设计了一种自适应反步控制方案。文献[11]针对一类含有广义不确定性的MIMO系统设计了一种块控反步控制方案。
前面所讨论的各种非线性设计方法都没有考虑系统具有不可测状态的情况,但是在很多实际问题中,往往不能测得全部状态变量,或由于经济或技术原因有一些状态变量不能测量[12-13]。在此情况下要想使上述非线性设计方法仍能发挥作用,需要设计状态观测器来根据测得的输出量估计出各状态变量[14-15]。非线性系统状态观测器的设计相对线性系统要复杂得多,目前还没有形成比较通用的设计方法,常用的方法有:类Lyapunov方法、高增益观测器、扩张观测器、自适应观测器和滑模观测器等[16-18]。滑模观测器对系统的形式没有特殊的要求,其鲁棒性只要求建模误差有界,所以一经提出就在工程实际中被广泛应用[19-20]。本文针对一类严格块反馈不确定非线性系统,基于反步法设计了L1自适应控制器,同时对系统不可观测状态设计了非线性滑模状态观测器。最后通过仿真算例验证了本文所设计控制方案的有效性。
1 问题描述
考虑如下严格块反馈型不确定非线性系统


本文的控制目标为设计控制器使得在存在不确定性σ(t)的情况下,系统(1)的输出y能够良好跟踪参考输入由于仅有输出状态x1可测,为了全状态反馈控制的需要,首先设计滑模状态观测器对未知状态进行估计。
式中,xi∈Rm(i=1,2,…,n)为状态变量,x1可测,初始状态‖x-n(0)‖≤ρ0<∞;y∈Rm为系统输出;u∈Rm为控制输入;fi∈Rm为非线性函数;gi∈Rm×m为控制增益矩阵;σ∈Rm为未知时变干扰。
首先给出以下假设:
假设1 系统不确定性σ(t)有界,且存在有界常数dσ>0,使得

假设2 非线性函数fi的偏导数分段连续且有界,且存在有界常数df>0,使得
2 观测器设计及收敛性分析
2.1 观测器设计
对系统(1),设计如下滑模观测器:

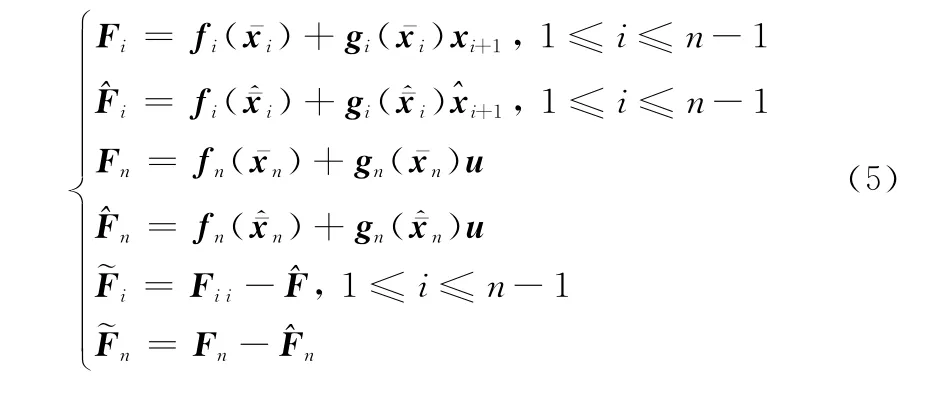
则式(1)减去式(4)可得估计误差动态为



则
定义滑模函数为
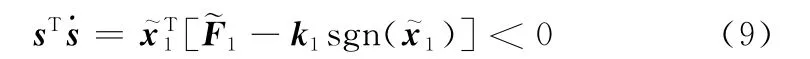
下面介绍k2,…,kn的选取方法。
式(6)是一个具有不连续项的微分方程,根据Philippov等效理论[19],其右侧可等效为滑模面两侧的两个系统的凸组合:

式中,0≤λ≤1;1≤i≤n-1;1≤j≤m。当系统进入滑模面之后,从而
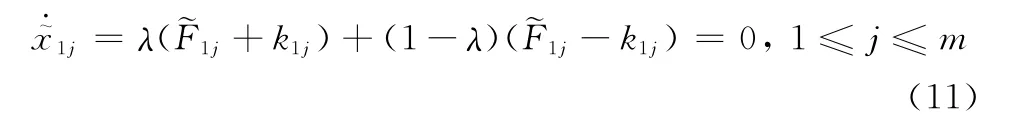
求解式(11)得

将式(12)代入式(10)得滑动面上的误差动态方程为

下面将根据式(13)来确定ki(2≤i≤n),使得观测误差渐近收敛,且具有一定的动态品质。根据文献[20]的思想,采用Jacobian线性化的方法。将误差系统(13)在观测器的工作点^xi,2≤i≤n附近线性展开得

式中

注1 该方法适用于工作状态变化范围不大的非线性系统,对于在较大范围内运行的非线性系统,可以采用分段线性化的方法得到切换增益,从而获得观测误差在全局范围内的一致性[19]。
2.2 收敛性分析
由于AHi为Hurwitz矩阵,因此存在正定矩阵P=PT满足Lyapunov方程其中Q=QT为任意正定矩阵。
定义Lyapunov函数
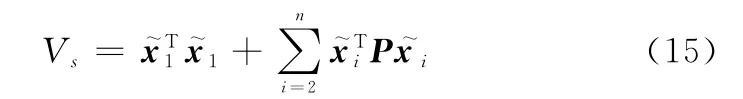
沿着系统轨线(14)对Vs求导得

将式(14)代入式(16)得

根据假设1及不等式λmin(Q)‖x‖2≤xTQx,其中λmin(Q)为Q的最小特征值,式(17)可转化为

3 L1自适应反步控制器设计及稳定性证明
控制目标为根据滑模观测器(4)得到的状态估计信息,设计L1自适应反步控制器,实现系统输出y对参考信号的跟踪,并满足一定的性能指标。为此先给出以下假设。
假设3 系统(1)的控制增益矩阵gi的逆矩阵存在且有界,即存在有界常数dg>0,使得

3.1 控制器设计
控制器设计采用反步技术方案,具体设计步骤如下。


式中,L1=>0。

选取Lyapunov函数

V1沿着系统轨线(22)的时间导数为
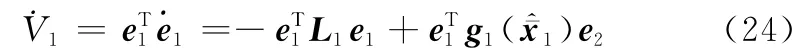
下一步将使e2=0,则˙V1<0。
步骤2 选择虚拟控制^x3的理想控制量为

式中,L2=>0。
定义跟踪误差e3=-,考虑状态观测器(4)的第2个子系统得

选取Lyapunov函数

V2沿着系统轨线(26)的时间导数为

下一步将使e3=0,则


选取Lyapunov函数

Vi沿着系统轨线(30)的时间导数为
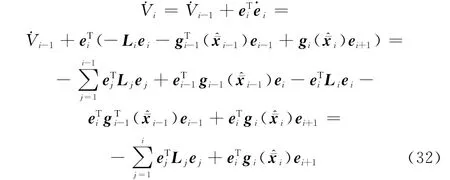
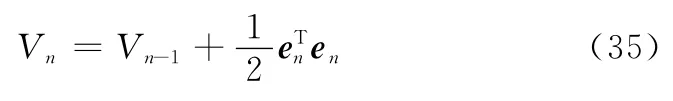
Vn沿着系统轨线(34)的时间导数为
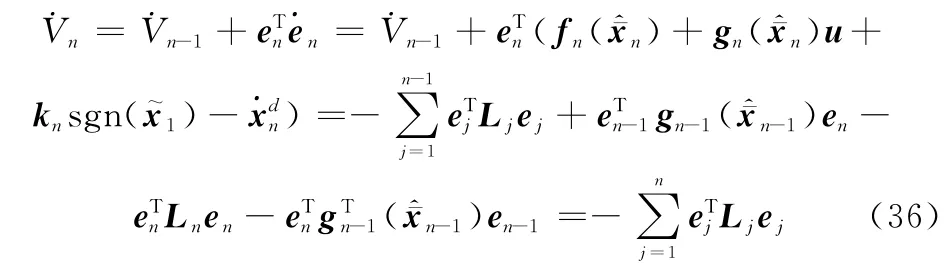
下一步将使ei+1=0,则
步骤n 选择理想控制量为

考虑状态观测器(4)的第n个子系统得

式中,Ln=LTn>0。
选取Lyapunov函数
由式(36)可知,控制量取(33)时,可实现系统(4)的渐近稳定,并实现系统输出对参考信号xd1的渐近跟踪。
然而,由式(29)和式(25)可知,虚拟控制信号xdi中含有符号函数sgn(·),不易求得其导数,而且对虚拟信号的求导会导致“项数膨胀”,从而造成计算载荷过大。为了消除这些问题,引入非线性跟踪微分器来提取微分信号。

式中,r>0为设计参数;x(t)为输入信号;z1为输入信号的跟踪值;z2为提取的微分信号。文献[21]已经证明该跟踪微分器能够快速跟踪输入信号与微分信号。
引入非线性跟踪微分器后,虚拟控制律xdi和理想控制律ud可重新表示为

考虑状态观测器(4)的第n个子系统,引入非匹配不确定项ε(t)补偿滑模观测器的逼近误差和非线性跟踪微分器的跟踪误差:

式中,不确定项ε(t)是一致有界的,存在已知紧凸集Δ使得ε(t)∈Δ,而且存在有界常数dε>0,使得

本步的控制目标为设计工程上易实现的L1自适应控制u保证系统(39)的输出跟踪,且具有良好的瞬态性能。
为了得到自适应律,首先定义状态预测器:

定义自适应律为


式中,f为光滑凸函数

式中,θmax为向量θ的范数最大值;εθ>0为投影容错界。
设计L1自适应控制律为


的Laplace变换;C(s)为稳定严真传递函数矩阵,其直流增益C(0)=I,C(s)的选择必须满足以下L1范数条件[23]:

式中,G(s)=(sI-Ag)-1(I-C(s)),L=max{dσ,df}。
3.2 稳定性证明

定义预测误差,由式(37)和式(41)得预测误差动态


选取Lyapunov函数

V对时间求导得
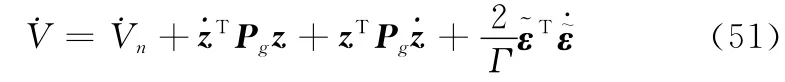
将式(36),式(48)和式(49)代入式(51)得

投影算子Proj(·)保证ε(t)∈Δ,因此下式成立


即

由式(52)和式(54)得

因此

此外,根据式(38)有

ε∈Δ
将式(57)、式(58)代入式(52)得

假设存在有界常数de使得‖ei(0)‖2≤de<∞,且z(0)=0,则

即系统内所有信号均有界,因此系统是稳定的。且由
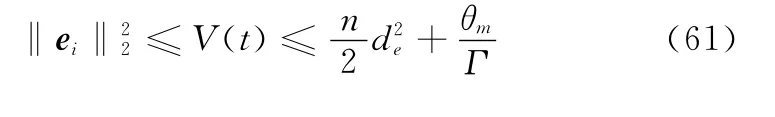
得系统对指令信号xd1的跟踪误差e1收敛于零的一个邻域:

且由式(62)可以看出,通过调整参数的值可以调节收敛域的大小。
4 数值仿真
为了验证本文所提出控制算法的有效性和实用性,本节采用文献[24]给出的四旋翼直升机姿态运动模型作为实例进行数值仿真。定义分别表征姿态角和角速度,四旋翼直升机姿态运动模型满足如下状态方程:

根据文献中的模型参数,式中

不确定项σ(t)表征模型参数不确定性(如转动惯量)和外部干扰(如阵风等)。
控制目标为在四旋翼角速度不可测的情况下,设计基于状态观测器的L1自适应控制器,使得四旋翼的姿态能够跟踪参考输入:
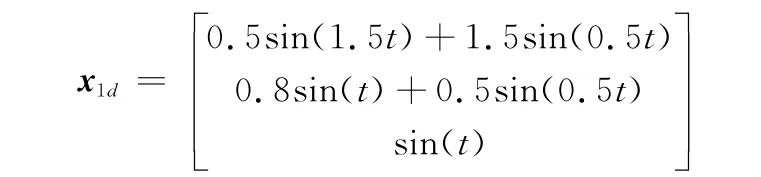
开始时间设为t=1,初始状态x01=[000]T。
所设计的鲁棒观测器和L1自适应控制器参数设置如下:

仿真结果如图1~图6所示。图1和图2分别为状态x1和x2的实际值和观测值。由图1和图2可知,本文设计的鲁棒状态观测器可以有效估计出系统的状态量,收敛速度较快,观测误差较小,状态x1的观测效果比x2的观测效果好。图3为系统输出跟踪效果,图4为跟踪误差。由图3可见,在系统具有不确定性的情况下,输出仍能很好地跟踪参考输入。由图4可知,跟踪误差保持在±0.1的范围内。图5为控制输入u,其时间导数如图6所示。由图5和图6可知,系统控制输入量较小且比较光滑,这是由于控制通道加入了低通滤波器的缘故,这降低了对系统执行器件的要求,更有利于工程实现。
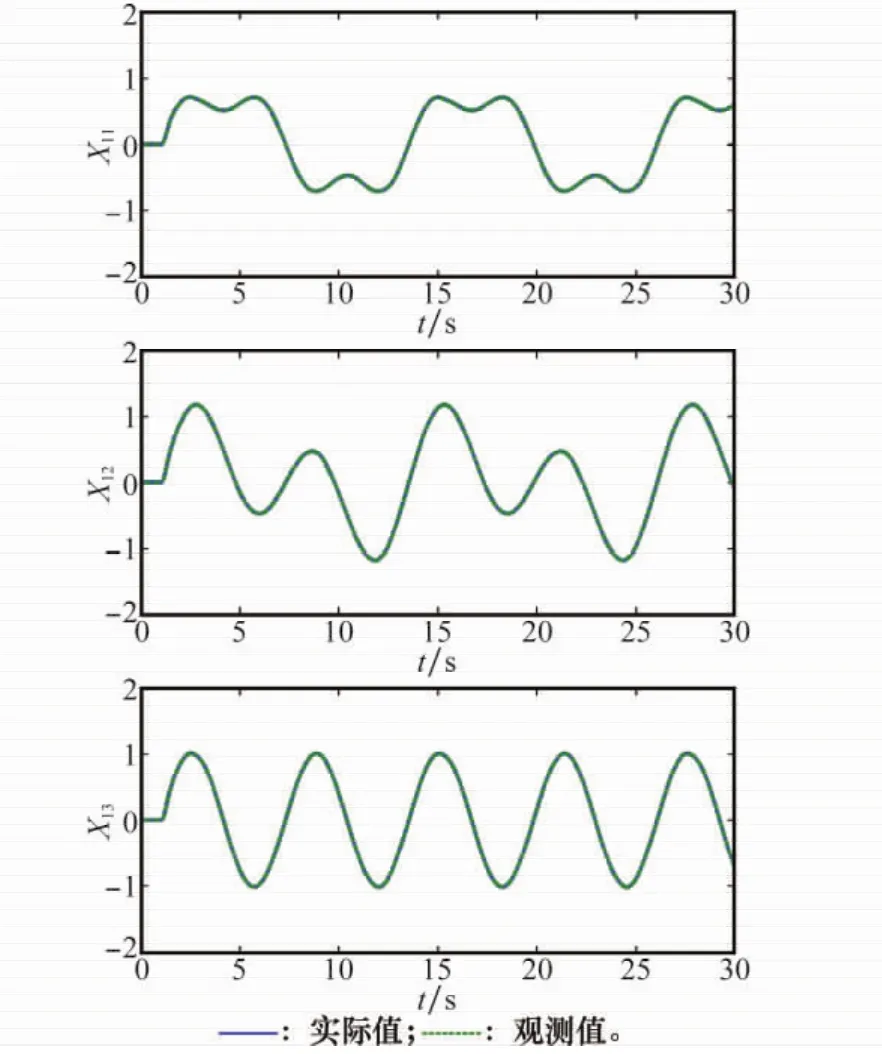
图1 x1实际值与观测值

图2 x2实际值与观测值

图3 系统输出值与参考输入值

图4 输出跟踪误差

图5 控制输入u

图6 控制输入u的时间导数
5 结 论
本文基于滑模状态观测器和L1自适应控制理论,针对一类状态不完全可测的严格块反馈型不确定非线性系统,用反步设计方法设计了一种新的控制方案。针对含有非匹配不确定性的原系统,设计了滑模鲁棒观测器对不可测状态进行了估计,并在理论上证明了该观测器的全局收敛性。引入了一个二阶非线性跟踪微分器来提取虚拟控制律的微分信号,消除了“项数膨胀”问题,减小了计算量。为了提高系统响应的瞬态性能和控制输入的平滑性,在反步控制的基础上引入了L1自适应控制,并对闭环系统的稳定性进行了证明。通过在四旋翼直升机姿态运动模型上的数值仿真,验证了该控制方案的有效性和良好性能。
[1]Tong S C,Li Y M.Adaptive fuzzy output feedback control of MIMO nonlinear systems with unknown dead-zone inputs[J].IEEE Trans.on Fuzzy Systems,2013,21(1):134-146.
[2]Chen C H,Lin C M,Chen T Y.Intelligent adaptive control for MIMO uncertain nonlinear systems[J].Expert Systems with Applications,2008,35(3):865-877.
[3]Zhang X,Lin Y.Adaptive output feedback tracking for a class of nonlinear systems[J].Automatica,2012,48(9):2372-2376.
[4]Chen M,Ge S S,How B V.Robust adaptive neural network control for a class of uncertain MIMO nonlinear systems with input nonlinearities[J].IEEE Trans.on Neural Networks,2010,21(5):796-812.
[5]Cao C,Hovakimyan N.L1adaptive controller for multi-input multi-output systems in the presence of unmatched disturbances[C]∥Proc.of the American Control Conference,2008:4105-4110.
[6]Zhang C J,Qi X G.Adaptive control of general nonlinear systems in strict feedback form[J].Control Theory &Applications,2006,23(4):621-626.(张承进,亓学广.一般严格反馈型非线性系统的自适应控制[J].控制理论与应用,2006,23(4):621-626.)
[7]Shi H L.A novel scheme for the design of backstepping control for a class of nonlinear systems[J].Applied Mathematical Modelling,2011,35(4):1893-1903.
[8]Chen M,Jiang C S,Wu Q X,et al.Adaptive output feedback control based on observer for a class of uncertain nonlinear systems[J].Systems Engineering and Electronics,2004,26(9):1250-1253.(陈谋,姜长生,吴庆宪,等.基于观测器的一类不确定非线性系统自适应输出反馈控制[J].系统工程与电子技术,2004,26(9):1250-1253.)
[9]Cao L J,Zhang S X,Liu Y N,et al.Flight controller design using adaptive parameter approximation block backstepping[J].Acta Aeronautica et Astronautica Sinica,2011,32(12):2259-2267.(曹立佳,张胜修,刘毅男,等.带有自适应参数近似的块控反步飞行控制器设计[J].航空学报,2011,32(12):2259-2267.)
[10]Chen M,Ge S S,Ren B.Adaptive tracking control of uncertain MIMO nonlinear systems with input constraints[J].Automatica,2011,47(3):452-465.
[11]Chang Y T.Block backstepping control of MIMO systems[J].IEEE Trans.on Automatic Control,2011,56(5):1191-1197.[12]Thienel J,Sanner R M.A coupled nonlinear spacecraft attitude controller and observer with an unknown constant gyro bias and gyro noise[J].IEEE Trans.on Automatic Control,2003,48(11):2011-2015.
[13]Besnard L,Shtessel Y B,Landrum B.Control of a quadrotor vehicle using sliding mode disturbance observer[C]∥Proc.of the AIAA Guidance,Navigation and Control Conference,2007:58-77.
[14]Zong Q,Tian B.Quasi-continuous high-order sliding mode controller and observer design for vehicle[C]∥Proc.of the 17th AIAA International Space Planes and Hyper-sonic Systems and Technologies Conference,2011:1-9.
[15]Doostdar P,Keighobadi J.Design and implementation of SMO for a nonlinear MIMO AHRS[J].Mechanical Systems and Signal Processing,2012,32(10):94-115.
[16]Zhao L L,Li P,Li X L.Adaptive observer design for a class of nonlinear systems[J].Control Theory &Applications,2012,29(1):11-18.(赵黎丽,李平,李修亮.一类非线性系统的自适应观测器设计[J].控制理论与应用,2012,29(1):11-18.)
[17]Ekramiana M,Sheikholeslamb F,Hosseinnia S.Adaptive state observer for Lipschitz nonlinear systems[J].Systems &Control Letters,2013,62(4):319-323.
[18]Dong Y,Mei S.State observers for a class of multi-output nonlinear dynamic systems[J].Nonlinear Analysis,2011,74(14):4738-4745.
[19]Liu Q,Yu D R,Wang Z Q.Sliding-mode observer design for ahypersonic vehicle[J].Acta Aeronautica et Astronautica Sinica,2004,25(6):588-592.(刘强,于达仁,王仲奇.高超声速飞行器的滑模观测器设计[J].航空学报,2004,25(6):588-592.)
[20]Chen J,Zhou S L,Song Z Q.Nonlinear modelling and openloop dynamatics characteristics for one hypersonic aircraft[J].Journal of Beijing University of Aeronautics and Astronautics,2011,37(7):827-832.(陈洁,周绍磊,宋召青.高超声速飞行器迎角观测器及控制器设计[J].北京航空航天大学学报,2011,37(7):827-832.)
[21]Han J Q.Active disturbance rejection control technique-the technique estimating and compensating the uncertainties[M].Beijing:National Defense Industry Press,2008.(韩京清.自抗扰控制技术—估计补偿不确定因素的控制技术[M].北京:国防工业出版社,2008.)
[22]Pomet J B,Praly L.Adaptive nonlinear regulation:estimation from the Lyapunov equation[J].IEEE Trans.on Automatic Control,1992,37(6):729-740.
[23]Xargay E,Hovakimyan N,Cao C.L1adaptive controller for multi-input multi-output systems in the presence of nonlinear unmatched uncertainties[C]∥Proc.of the American Control Conference,2010:874-879.
[24]Guiherme V,Manuel G,Francisco R.An integral predictive/nonlinear H∞control structure for a quadrotor helicopter[J].Automatica,2010,46(1):29-39.
L1adaptive control for a class of uncertain nonlinear systems based on observer
QI Xiao-hui,ZHEN Hong-tao,DONG Hai-rui
(Department of UAV Engineering,Ordnance Engineering College,Shijiazhuang 050003,China)
A novel L1adaptive control strategy based on a sliding mode observer using a back-stepping design method for a class of uncertain nonlinear systems in a strict block feedback form is presented.Due to the incompletely observable system states,a sliding mode observer is designed to estimate system states,and the convergence is analyzed.Moreover,the ideal control law is derived through the back-stepping method.In order to overcome the“terms explosion”problem,a nonlinear tracking differentiator is used to extract differential signals of virtual control.In order to improve the transient performance of system response and eliminate the highfrequency chatter of the control input,the L1adaptive control is introduced to improve the control laws and the stability of the system is proved.Finally,a numerical simulation is given to demonstrate expected performance of the proposed control scheme.
nonlinear system;sliding mode observer;L1adaptive control;backstepping control
TP 273
A
10.3969/j.issn.1001-506X.2015.08.23
齐晓慧(1962-),女,教授,博士研究生导师,主要研究方向为自适应控制理论、无人飞行器导航与控制。
E-mail:zuoluo_009@163.com
甄红涛(1986-),男,博士研究生,主要研究方向为非线性系统自适应控制。
E-mail:zhenhot@163.com
董海瑞(1977-),男,讲师,主要研究方向为无人飞行器导航与控制。
E-mail:824718646@qq.com
1001-506X201508-1866-08
网址:www.sys-ele.com
2014-05-05;
2014-09-20;网络优先出版日期:2015-01-06。
网络优先出版地址:http://www.cnki.net/kcms/detail/11.2422.TN.20150106.1157.001.html
军队预先研究基金资助课题

