层析合成孔径雷达成像航迹分布优化方法

毕 辉，蒋成龙，王万影，张冰尘，洪 文

（1.中国科学院电子学研究所微波成像技术重点实验室，北京100190；2.中国科学院大学，北京100190）

层析合成孔径雷达成像航迹分布优化方法

毕 辉1，2，蒋成龙1，2，王万影1，2，张冰尘1，洪 文1

（1.中国科学院电子学研究所微波成像技术重点实验室，北京100190；2.中国科学院大学，北京100190）

层析合成孔径雷达成像（tomography synthetic aperture radar，TomoSAR）将合成孔径原理用于高程向，通过不同入射角的多幅二维合成孔径雷达图像对高程向反射功率进行重建，从而实现三维成像。TomoSAR中，航迹分布是影响高程向重建的重要因素。针对高程向分布稀疏的情形，压缩感知方法被用于TomoSAR。基于压缩感知的TomoSAR中高程向重建质量取决于观测矩阵的性质，而航迹分布与观测矩阵的重构性能紧密相关。利用一种基于相关系数的观测矩阵优化准则，对航迹分布进行参数优化，从而在航迹数目一定的情况下，实现高程向的优化重建。仿真和实验结果验证了该方法的有效性。

层析合成孔径雷达成像；压缩感知；相关系数；航迹优化；观测矩阵

0 引 言

层析合成孔径雷达成像（tomography synthetic aperture radar，TomoSAR）将合成孔径原理用于高程向［1］，利用同一场景的多幅二维SAR图像（不同的入射角）在高程向上进行孔径合成以获取高程向分辨率，从而实现三维成像。Tomo SAR成像中，高程向分辨率与高程向孔径大小密切相关，而有限的航迹数目约束了高程向孔径大小，使得高程向分辨率低于方位向和距离向。2000年，借助于德国宇航局（DLR）E-SAR机载系统的森林数据［2］，Reigber等利用谱估计方法获得了观测区域2～3m的高程向分辨率［1］。2005年，Fornaro利用欧洲资源卫星（Enrope resource satellite，ERS）19条航迹的C波段数据实现了对意大利那不勒斯海湾的7.9m高程向分辨率成像［3］。

针对高程向分布稀疏的情况，压缩感知［4－6］方法被用于Tomo SAR成像，从而实现了高程向的超分辨。根据压缩感知理论，在特定的条件下，稀疏信号可以以远低于香农－奈奎斯特采样定理所需要的样本数目实现准确重建。因此，压缩感知是一个可以有效减少航迹数目同时获取高程向准确重建的方法。然而为了保证高程向的重建精度仍需较多的航迹数目。2009年，文献［7］进行了基于压缩感知的Tomo SAR成像仿真。2010年，借助于德国宇航局TerraSAR-X超高分辨率星载数据，文献［8］阐述了压缩感知用于Tomo SAR成像中的超分辨能力。

压缩感知重建中，观测矩阵需要满足一定的约束条件。其中，限制等距条件（restricted isometry property，RIP）［6］、零空间性质（null space property，NSP）［6］、限制正交条件（restricted orthogonality property，ROP）［9］、精确重建条件（exact reconstruction criteria，ERC）［11］和相关性条件（coherence）［6，9－10］等常用来对观测矩阵进行评判，然而RIP、NSP、ROP、ERC评判准则都难于计算，相比而言，相关性条件计算简单且可以对观测矩阵进行有效的评估。文献［12－13］证明了信号压缩感知重建的质量与观测矩阵的相关系数密切相关，因而可用对观测矩阵的相关系数的约束来实现信号的优化重建。目前，最大相关系数和t%平均相关系数准则已被用于评价聚束SAR的在不同采样策略下的稀疏重建质量［11，14］；文献［15］利用平均相关系数实现了多发多收压缩感知雷达采样策略的优化。

基于压缩感知的Tomo SAR成像中，观测矩阵与航迹分布密切相关。目前还未有利用相关性条件进行Tomo SAR成像中航迹分布优化方面的研究。本文针对基于压缩感知的Tomo SAR成像中航迹分布问题，利用一种观测矩阵的相关系数最优化准则，对航迹分布进行优化，从而保证在航迹数目一定的情况下，获取能够对高程向进行优化重建的航迹分布。

1 Tomo SAR成像模型

Tomo SAR成像中每个航迹获取的回波数据都可以由经典二维成像算法重建为一幅二维SAR图像，利用多航迹获取的多幅经过误差校正和配准之后的二维SAR图像，可以实现高程向的分辨。

如图1所示，Tomo SAR成像中，在第m条航迹高度bm处，一个方位－距离分辨单元（x0，r0）处的第m个观测值ym（x0，r0）可以表示为沿着高程向的反射函数的叠加

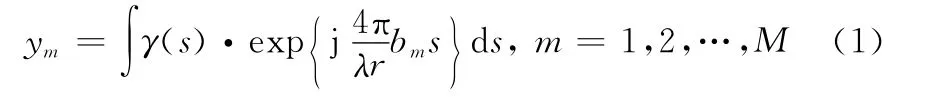
式中，s表示在一个方位－距离分辨单元上的高程向距离；γ（·）是沿着高程向s的反射函数；λ为发射脉冲的波长；r表示平台到s处目标的瞬时距离。

将高程向s在其范围Δs内离散化为L个均匀分布的点sl（l＝1，2，…，L），则第m个航迹处观测数据为

式中，列向量y、γ与n分别表示方位－距离分辨单元（x0，r0）处的观测数据、高程向的反射函数以及观测噪声；观测矩阵Φ中第m行l列上的元素为

针对高程向稀疏分布场景，根据成像模型（3），本文对高程向反射函数进行压缩感知重建

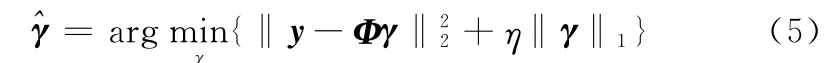
式中，η是根据噪声水平约束的正则化参数；＾γ为重建的高程向反射函数。

图1 层析SAR成像几何

2 基于相关系数的Tomo SAR成像航迹分布的优化

观测矩阵Φ的第l与l′列之间的相关系数定义如下：

式中，ul表示单位阵的第l列。

2.1 基于相关系数的优化准则

最近提出了一种基于相关系数的观测矩阵的优化准则

式中，dp表示观测矩阵相关系数的支撑集半径

其中

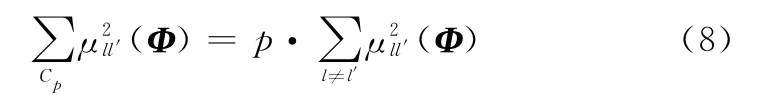
集合Cp中的元素构成了观测矩阵相关系数中能量最大p（0＜p＜1）的部分。0＜βp＜1表示相关系数支撑半径的上界。

上述优化准则中，约束条件表征了压缩感知重建时观测矩阵相关系数区域的半径，约束了压缩感知重建时允许出现的误差范围。支撑半径和平均相关系数越小，则压缩感知重建的效果越好。当观测矩阵是正交阵时，∀l≠l′有μll′（Φ）＝0且dp（Φ）＝0。

2.2 基于相关系数的Tomo SAR成像航迹优化准则

根据式（6）中相关系数的定义，式（4）中层析SAR成像的观测矩阵第l与l′列之间的相关系数可以表示为

将式（9）代入式（7），可以得到层析SAR成像的航迹优化准则

遍历所有满足条件的航迹分布策略，求得满足式（10）中的优化准则的航迹分布。该航迹分布即为在基于相关系数的观测矩阵约束条件下，层析SAR成像中高程向进行压缩感知重建的优化航迹分布。

3 仿真实验结果与分析

本节将通过仿真和实验验证所提出的基于相关系数的层析SAR成像航迹优化准则，并通过分析仿真和实验结果说明上述方法的有效性。

3.1 仿真

仿真中认为所有航迹距观测的方位－距离分辨单元的水平距离相同，竖直距离不同。仿真参数设计为：参考航迹斜距（高度最低的航迹）为4 000m，参考航迹入射角为60°，观测的方位－距离分辨单元的高程向高度为100m，发射脉冲波长为0.86m。高程场景模拟森林区域的树冠和地面的两层分布（两个散射中心）。其中高程向上的地面和树冠两个散射中心分别在20m和70m处，散射强度比为1∶2。

利用相对均方误差（relative mean square error，RMSE）和虚警率（false alarm rate，FAR）作为评价高程向重建误差的标准。RMSE的定义为

FAR的定义为

选取航迹数目为9，信噪比为20dB，进行1 000次蒙特卡罗仿真。每次仿真中，利用本文所提出的航迹优化方法得到的优化航迹分布，通过采集到的观测数据，对高程向进行压缩感知重建，记录观测矩阵的相关系数值、重建的相对均方误差及虚警率。

表1给出了1 000次蒙特卡罗仿真中，观测矩阵相关系数、重建的相对均方误差及虚警率的分布情况。由表1可以看出，重建的相对均方误差及虚警率的分布正比于观测矩阵相关系数，这说明观测矩阵相关系数可以准确表征重建的相对均方误差及虚警率变化，观测矩阵相关系数越大，重建的相对均方误差及虚警率越大。图2分别给出了重建的相对均方误差及虚警率与观测矩阵相关系数的分布关系。由图2可以看出，相关系数较小时，重建的相对均方误差及虚警率随观测矩阵相关系数线性变化。当相关系数过大时（本文中约大于0.22），观测矩阵列与列之间的相关性较高，使得观测矩阵的压缩感知重构性能降低，导致相对均方误差及虚警率增大。这也说明了观测矩阵的相关系数越小，高程向的压缩感知重建效果越好。

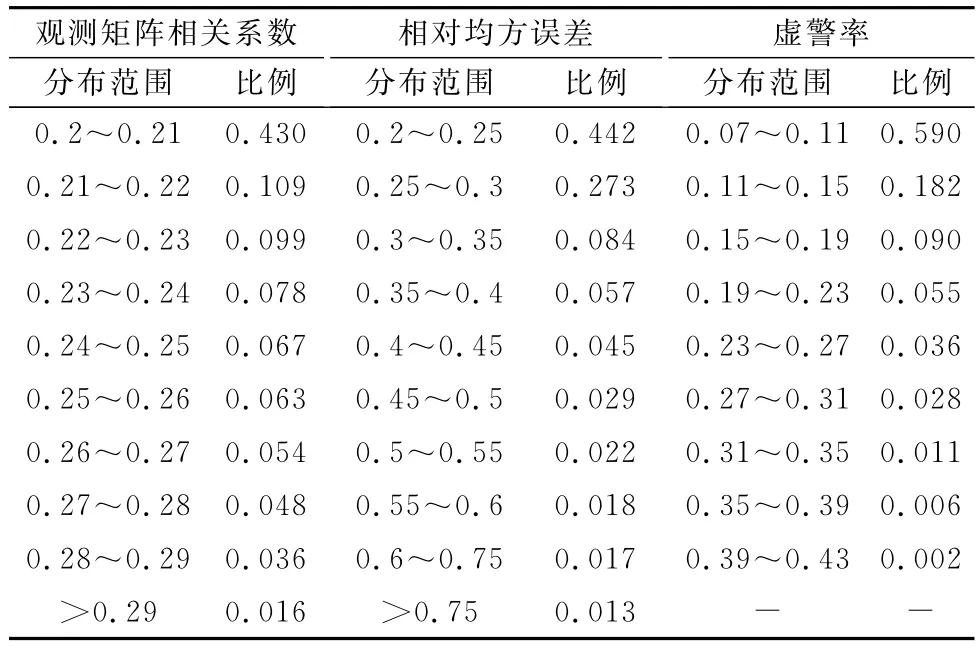
表1 观测矩阵相关系数、相对均方误差、虚警率分布

图2 误差分析

图3给出了航迹数目为9时，利用本文中优化方法计算的航迹分布与随机航迹分布、均匀航迹分布及优化的均匀航迹分布对高程向进行压缩感知重建的结果。需要说明的是，优化的均匀航迹分布同样是通过本文中的优化方法计算得到，只是其表征所有均匀航迹分布（所有相邻航迹之间的距离相同，但距离值可以变化）中最优的。由图3（a）可以看出，除均匀航迹分布之外，另3种分布均能实现对高程向的重建，获取两个散射中心的位置。由图3（b）和图3（c）可知，利用本文中航迹优化方法优化的航迹分布相比于优化的均匀航迹以及随机航迹分布，其重建结果更接近于模拟的高程向分布。

图3 不同航迹分布对高程向进行压缩感知重建的结果

由上述分析可知，较其他航迹分布策略，本文中航迹分布优化方法获取的航迹分布可以实现高程向优化重建，这也反映了本文中所提出的航迹优化方法的有效性。

图4给出了观测矩阵相关系数及高程向重建的相对均方误差随航迹数目的变化曲线。由图4可以看出，航迹数目不同的情况下，相比于其他3种航迹分布，本文所述的优化方法得到的航迹分布构建的观测矩阵相关系数小于另3种航迹分布，且压缩感知重建结果具有较小的相对均方误差。

3.2 实验

为进一步说明该方法的有效性，本文利用由德国宇航局的E-SAR传感器于2007年获取的瑞典南部森林区域的P波段10条航迹BioSAR数据进行实验验证［16］。该数据重建的二维SAR图像的方位向分辨率为4.0m，距离向分辨率为2.1m。在所有数据中，选取其中的8条进行高程向重建，本节比较了所提出的航迹优化方法选取的航迹分布策略与其他航迹分布策略的高程向成像结果。图5（a）给出了全部10条航迹数据对高程向进行重建的结果，图5（b）表示航迹数目为8时，优化的航迹分布的高程向重建结果，图5（c）和图5（d）则给出了从10条航迹中随机选取8条航迹后的高程向重建结果。由图5可知，8条航迹下的优化航迹分布的高程向重建结果接近于10条航迹的结果，可以准确重建地面和树冠两层区域，而图5（c）和图5（d）中的重建结果中均出现了无法区分地面和树冠两层散射中心的现象（如图中矩形框内的区域所示）。图5（b）、图5（c）和图5（d）中不同航迹分布策略的观测矩阵的相关系数的大小也准确反映了高程向的重建结果，相关系数越小，高程向重建效果越好。这也说明了本文中基于相关系数的航迹优化准则的有效性。

图4 不同航迹分布对高程向的重建指标比较

4 结 论

本文研究了观测矩阵相关系数对于基于压缩感知的Tomo SAR成像高程向重建性能的影响，通过基于相关系数的航迹优化准则实现了对压缩感知Tomo SAR成像中航迹分布的优化，并通过仿真和实验验证了所提出的Tomo SAR成像航迹优化准则的有效性。文章的主要贡献为：针对Tomo SAR成像模型，给出了基于相关系数的Tomo SAR成像的航迹分布优化准则；在航迹数目一定的情况下，通过该优化准则能够获取对高程向进行压缩感知重建的最优航迹分布。

利用本文中的优化准则，可以分析实际数据中航迹分布的有效性。未来可以作为Tomo SAR成像飞行实验航迹设计的一个参考，以减少不必要的飞行航迹，降低飞行成本。

图5 不同航迹分布策略下森林区域压缩感知重建结果

［1］Reigber A，Moreira A.First demonstration of airborne SAR tomography using multibaseline L-band data［J］.IEEE Trans.on Geoscience and Remote Sensing，2000，38（5）：2142－2152.

［2］Horn R.The DLR airborne SAR project E-SAR［C］∥Proc.of the International Geoscience and Remote Sensing Symposium，1996：1624－1628.

［3］Fornaro G，Lombardini F，Serafino F.Three-dimensional multipass SAR focusing：Experiments with long-term spaceborne data［J］.IEEE Trans.on Geoscience and Remote Sensing，2005，43（4）：702－714.

［4］Donoho D.Compressed sensing［J］.IEEE Trans.on Information Theory，2006，52（4）：1289－1306.

［5］Candes E J，Tao T.Near-optimal signal recovery from random projections：Universal encoding strategies［J］.IEEE Trans.on Information Theory，2006，52（12）：5406－5425.

［6］Candes E，Romberg J，Tao T.Stable signal recovery from incomplete and inaccurate measurements［J］.Communications on Pure and Applied Mathematics，2006，59（8）：1207－1223.

［7］Budillon A，Evangelista A，Schirinzi G.SAR tomography from sparse samples［C］∥Proc.of the IEEE International Geoscience and Remote Sensing Symposium，2009：865－868.

［8］Zhu X，Bamler R.Very high resolution spaceborne SAR tomography in urban environment［J］.IEEE Trans.on Geoscience and Remote Sensing，2010，48（12）：4296－4308.

［9］Candes E，Tao T.Decoding by linear programming［J］.IEEE Trans.on Information Theory，2005，51（12）：4203－4215.

［10］Tropp J.Greed is good：algorithmic results for sparse approximation［J］.IEEE Trans.on Information Theory，2004，50（10）：2231－2242.

［11］Patel V M，Easley G R，Healy D M，et al.Compressed synthetic aperture radar［J］.IEEE Journal of Selected Topics in Signal Processing，2010，4（2）：244－254.

［12］Candes E，Romberg J.Sparsity and incoherence in compressive sampling［J］.Inverse Problems，2007，23（3）：969－985.

［13］Donoho D，Huo X.Uncertainty principles and ideal atomic decomposition［J］.IEEE Trans.on Information Theory，2001，47（7）：2845－2862.

［14］Stojanovic I，Çetin M，Karl W C.Compressed sensing of monostatic and multistatic SAR［J］.IEEE Geoscience and Remote Sensing Letters，2013，10（6）：1444－1448.

［15］Yu Y，Petropulu A P，Poor H V.Measurement matrix design for compressive sensing-based MIMO radar［J］.IEEE Trans.on Signal Processing，2011，59（11）：5338－5352.

［16］Hajnsek，I，Scheiber R，Ulander L，et al.BioSAR 2007tech-nical assistance for the development of airborne SAR and geophysical measurements during the BioSAR 2007experiment：Final report without synthesis［R］.European Space Agency，2008.

Track distribution optimization for tomographic synthetic aperture radar imaging

BI Hui1，2，JIANG Cheng-long1，2，WANG Wan-ying1，2，ZHANG Bing-chen1，HONG Wen1
（1.Science and Technology on Microwave Imaging Laboratory，Institute of Electronics，Chinese Academy of Sciences，Beijing 100190，China；2.University of Chinese Academy of Sciences，Beijing 100190，China）

Tomography synthetic aperture radar（TomoSAR）extends the synthetic aperture principle into elevation.It uses measured repeat-pass synthetic aperture radar data to reconstruct the backscattered power along elevation，and achieves a three-dimensional（3-D）image.In TomoSAR，track distribution affects the quality of elevation reconstruction.Compressive sensing（CS）is used to the elevation reconstruction for the sparse elevation distribution.The imaging quality of TomoSAR based on CS depends on the recovery property of the measurement matrix，which is affected by the track distribution.An optimal criterion based on coherent coefficient is used to optimize the distribution of flight tracks，and achieve the optimal reconstruction of elevation when the amount of tracks is fixed.Simulated and experimental results validate the effectiveness of the optimized method.

Tomography synthetic aperture radar（TomoSAR）；compressive sensing（CS）；coherent coefficient；track optimization；measurement matrix

TN 958

A

10.3969／j.issn.1001-506X.2015.08.11

毕 辉（1991－），男，博士研究生，主要研究方向为稀疏微波成像、层析合成孔径雷达成像。

E-mail：bihui1991＠163.com

蒋成龙（1987－），男，博士研究生，主要研究方向为合成孔径雷达成像、稀疏微波成像。

E-mail：jiangcl＠mail.ustc.edu.cn

王万影（1989－），女，硕士研究生，主要研究方向为层析合成孔径雷达成像。

E-mail：wangwanying0913＠126.com

张冰尘（1973－），男，研究员，博士，主要研究方向为雷达信号处理、新体制雷达。

E-mail：bczhang＠mail.ie.ac.cn

洪 文（1968－），女，研究员，博士，主要研究方向为三维微波成像的新概念、新方法。

E-mail：whong＠mai.ie.ac.cn

1001－506X201508－1787－06

网址：www.sys－ele.com

2014－08－27；

2014－12－30；网络优先出版日期：2015－03－30。

网络优先出版地址：http：／／www.cnki.net／kcms／detail／11.2422.TN.20150330.0832.002.html

国家重点基础研究发展计划（973计划）（2010CB731900）资助课题