基于传感器网络的在线决策融合目标检测方法
闫永胜,王海燕,董海涛,姜 喆
(西北工业大学航海学院,陕西西安710072)
基于传感器网络的在线决策融合目标检测方法
闫永胜,王海燕,董海涛,姜 喆
(西北工业大学航海学院,陕西西安710072)
针对传感器网络(sensor network,SN)目标融合检测应用中融合中心无法精确地获得局部传感器节点检测性能参数的问题,建立了基于SN的目标融合检测系统,提出了一种非理想信道条件下在线决策融合的目标检测方法。该方法依据解调后数据构建了节点未知虚警概率、检测概率以及节点与融合中心信道平均传输错误概率等未知参数求解模型,并采用非线性最小二乘方法在线地估计出这些未知参数。进而通过选择性能优的节点参与融合,最大化融合检测系统检测概率。仿真结果表明:这种在线决策融合方法能够准确地估计出传感器节点的概率参数以及信道的平均传输错误率;相比于已知先验的最优似然比融合规则,在线决策融合规则检测性能相当。
传感器网络;目标检测;在线决策融合;非线性最小二乘
0 引 言
随着无线通信、嵌入式技术以及微机电系统的发展,使得无线传感器网络(wireless sensor networks,WSNs)技术的大规模应用成为可能[1-2]。WSN是由分布在监测区域内的大量传感器节点通过无线通信方式形成自组织网络,常用于民用生活领域[3-6],如空气监测,森林火灾监测,海啸预警等,也用于军事领域[7-8],如目标检测、目标参数估计、战场态势评估等。基于WSN的目标检测系统具有快速布放、抗毁性强等优点,该技术有着广阔的应用前景,本文重点研究基于WSN目标检测决策融合方法,以期通过数据融合方式提高目标检测性能。
与WSN目标检测相关的早期研究主要是分布式检测,国内外学者进行了诸多尝试,并取得了一定进展,主要集中于最优决策规则求解以及门限确定两方面[9]。对于并行拓扑的分布式检测,文献[10]总结了在传感器节点间观测独立假设下,融合中心最优融合规则、传感器节点最优决策规则均是似然比检测(likelihood ratio test,LRT)。随着WSN技术的发展,将分布式检测应用于WSN存在着新的挑战:WSN中局部传感器节点与融合中心之间有限带宽资源,传输信道的衰落与干扰引入的信息不可靠传输,以及传感器节点有限的能量资源等。因此,需要寻求适合于WSN的目标决策融合检测方法,使其在一定限制条件下更加有效地检测到目标。文献[11-12]以传感器节点与融合中心之间的衰落信道为出发点,构建了融合中心最优的LRT融合规则。文献[13-14]以WSN目标检测系统消耗能量为出发点,采用多目标优化算法同时优化系统能量消耗与系统检测性能,提出了更加切合实际的最优决策融合规则。这些最优的LRT融合规则取决于参与融合传感器节点的检测性能(检测概率和虚警概率)和传输信道的实时增益或信道统计特性,但是在实际应用中,这些参数是未知的,即使节点的检测概率、虚警概率可以通过在线实验确定,但是传输这些结果到融合中心需要额外地消耗节点有限的能量资源、有限的信道资源,且在求取平均比特错误率时,需要通过发送训练序列得到其估计,进一步增加了节点的资源消耗。基于此,文献[15]提出了一种在线迭代方法估计出传感器节点的检测概率、虚警概率等,进而采用最优LRT规则进行融合,在Bayes准则下得到了较小的错误概率。但是,该在线迭代方法假设传感器节点与融合中心之间信道是理想的,仅仅适合于可靠通信条件下的分布式检测,对于WSN背景下目标决策融合检测,信道特性会影响决策融合的目标检测性能[16]。
本文在传感器网络(sensor network,SN)目标检测系统非理想传输信道的基础上,提出了一种在线迭代的决策融合目标检测方法,该方法首先依据融合中心解调数据得到各个传感器节点无条件概率的序贯估计值,其次,通过迭代在线地估计出每个传感器节点的检测概率,虚警概率,以及平均传输错误概率,再次,依据最优的LRT融合规则选择合适的传感器节点参与融合,最后,融合得到最终判决输出。
1 无线传感器网络目标检测模型
考虑如图1所示的WSN目标检测系统,由N个传感器节点和1个融合中心组成,N个节点周期性地采集环境信息,并依据局部判决规则ui=γi(xi),∀:i=1,2,…,N输出局部判决结果ui,节点将局部判决结果以一定的调制方式经非理想传输信道传输到融合中心,融合中心将得到的信号解调得到yi,依据融合规则u0=γ0(yi)输出最终判决u0∈{0,1},0表示没有目标,1表示目标出现。

图1 目标检测系统示意图
1.1 局部判决层
假设第i个传感器节点在k时刻接收到的数据为
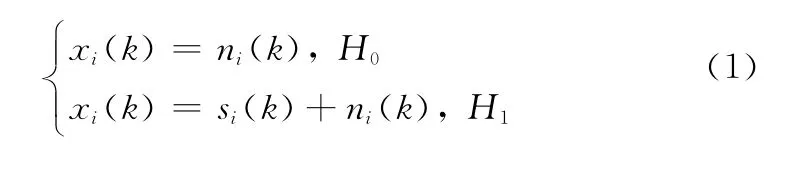
式中,si(k)是k时刻采集到的信号;ni(k)是均值为0方差为σ2
ki的高斯白噪声,即ni(k)~N(0,)。考虑到实际的检测系统,每个传感器节点每次采集M个点xi(k)=[(k),(k),…,(k)],进行局部判决。为了减少传感器节点向融合中心传输的数据量,我们假设节点进行1bit量化,即ui∈{0,1}。假设目标辐射噪声信号为一随机过程且si(k)~N(0,),似然比检测是能量检测器[17],则第i个传感器节点、第k次检测的虚警概率和检测概率分别为
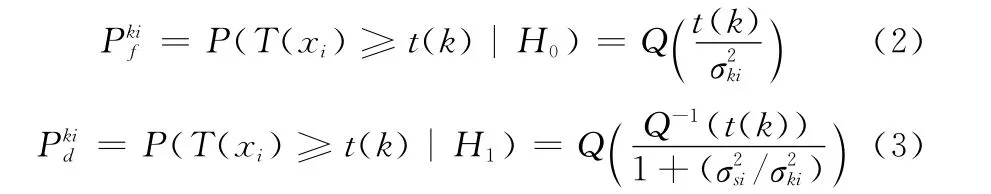
式中,Q(·)是标准正态分布的累积分布函数。假设目标各向同性地向外辐射能量,传感器节点接收到信号能量为

式中,di是第i个节点距目标的距离,表示为

由式(2)~式(5)可以看出,传感器节点的检测概率是目标位置、奈曼-皮尔逊(Neyman-Pearson)准则下给定的虚警概率以及环境噪声方差的函数。
1.2 信道传输层

式中,Pe是传输信道的平均比特错误率,不同通信信道条件下Pe具有不同形式,表1给出了二进制相移键控(binary phase shift keying,BPSK)、二进制频移键控(binary frequency shift keying,2FSK)调制时不同通信信道下的平均比特错误率[19]。

表1 不同通信信道条件下的平均比特错误率
表1中,γb是高斯信道的传输信噪比是瑞利衰落信道的平均传输信噪比。

由式(7)可知,对于1bit传输的目标融合及检测系统而言,非理想信道的平均传输错误概率等于平均比特错误率。
1.3 最优融合层
当传感器间观测条件独立时,最优对数LRT可以表示为

式中,T为融合中心的融合门限。由式(8)可知,融合中心需要获取每个传感器节点检测概率和虚警概率,即使当传感器节点采用Neyman-Pearson准则时,已知,仍需要检测概率的先验知识,而传输这些参数到融合中心需要额外地消耗节点有限的能量,需要占用通信信道有限的带宽资源。文献[18]在非理想信道条件下,构建了一种融合规则——等增益合并(equal gain combining,EGC)融合规则:

该融合规则不需要传感器节点的检测性能参数,所有节点赋予相同的权值,都为1。可以证明,当目标距WSN等效中心距离远大于WSN内传感器节点之间距离时,EGC的检测性能等效于最优LRT融合规则的检测性能[20]。
2 在线决策融合方法
2.1 非理想信道下的参数估计
实际目标融合检测系统中,H1/H0的先验分布以及局部传感器节点的检测性能未知,融合中心仅获得了局部传感器节点传输到融合中心的带噪解调决策值(i=1,2,…,N;l=1,2,…,L),其中,L是每个节点做出的决策值数目。本文提出的在线决策融合目标检测方法在传感器节点与融合中心之间非理想传输信道的假设下,依据融合中心解调后的局部传感器节点决策值在线地估计出未知参数,因此相应的融合规则称作在线融合规则。
对于二元假设检验问题,具有N个传感器节点的目标检测系统共有K=2N个决策组合,每组决策组合出现的概率为

式中,k1,…,kN∈{0,1};P(H1)≜π1表示假设检验中H1的先验概率;P(H0)=1-P(H1)≜π0表示H0的先验概率。式(10)可以进一步表示为


决策组合概率Pk(k=1,2,…,K=2N)可以通过时间平均来逼近,即

式中,L(y1=k1,…,yN=kN)是组合(y1=k1,…,yN=kN)在所有L次决策组合中出现的次数。一般地,时间平均值存在着估计误差ek,有


式中,对于N个传感器节点目标检测系统而言,共有K=2N个等式,由于,因此有K-1个独立等式,θ中未知参数个数为2 N+2。依据式(15)可以获得未知参数θ的非线性最小二乘(nonlinear least square,NLS)估计,即

式中,P=f(θ)是未知参数θ的函数。
非理想信道条件下未知参数θ的估计问题转化为求解式(16),即获得NLS估计。需要注意的是,未知参数约束为

因此,可以通过求解如下带约束的NLS问题得到未知参数的估计
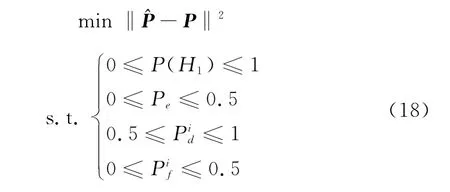
带约束的NLS问题式(18),可以通过遗传算法、模拟退火算法、禁忌搜索法等智能优化算法求解。本文采用Matlab中的lsqnonlin函数,求解方法是Trust-Region-Reflective优化算法(具体参考文献[21])。
2.2 在线决策融合
为了获得式(13)的时间平均,需要存储大量的节点决策值以及等待一定的时间,这对于实时目标检测系统而言是不切实际的。一种可行方法是采用序贯求解的方式,每次计算窗内^Pk,随着局部传感器节点序贯地传输局部判决数据到融合中心,融合中心实时地在线跟踪局部传感器节点检测性能以及非理想信道的平均比特错误率的变化。
融合中心接收到每个节点的解调数据后,设置窗长度为L,滑动长度为T,依据式(13)得到的组合概率,写成递归形式,有

2.3 运算复杂度
本文提出的在线决策融合中,带约束的非线性最小二乘多参数估计方法的时间消耗主要集中在两个方面:①时间平均需要较多次的局部传感器节点决策值;②求解非线性最小二乘问题。对于①,较少的传感器节点决策值会大大影响估计精度,这一结论可以由后续的仿真得出,因此,本文提出了在决策融合初期,融合中心采用次优的计数融合统计量来做出有无目标的判断。当融合中心得到较多来自节点的决策值(大于2 000)后,采用本文提出的迭代方法在线地估计传感器节点的检测概率等参数。对于②,运算复杂度为O(nm2)[22],n表示最小二乘问题中求和函数个数,m表示问题的规模,即未知数的个数,在本应用中,n=2N,m=2 N+2,因此,运算复杂度为O(2N(2 N+2)2)。由此可以看出,求解非线性最小二乘问题的运算量随着传感器节点数的增加而呈指数增长,这是由于方程的个数2N随节点数增长而指数增长。
2.4 节点选择
当融合中心获得每个传感器节点检测概率,虚警概率以及信道平均比特错误率后,选取一定数目的传感器节点参与融合判决,以达到一定准则下最优检测性能目的。N个传感器节点选取p个参与融合共有种选择,当传感器节点数目较少时,可以依据最优的LRT融合规则对比每种配置下的检测性能,从而选择Neyman-Pearson准则下检测概率最大的配置。
图2给出了N=4和N=3情况下接收机特性曲线(receiver operating characteristic,ROC)。4个节点检测概率分别为Pd=[0.80,0.85,0.90,0.60]T,虚警概率分别为Pf=[0.02,0.02,0.02,0.02]T,信道的平均比特错误率为Pe=0.12。图中3个传感器节点是指剔除第4个节点(P=0.6,P=0.02)后的检测性能。由图2可以看出,非理想信道条件下,一个质量较差的传感器节点(P=0.6,P=0.02)会引起系统检测性能下降,因此,通过选择合适的传感器节点参与融合,一方面能够通过剔除性能较差节点达到提高系统检测性能的目的,另一方面,可以通过反馈的方式控制该节点停止工作,以节约整个基于SN目标检测系统的能量。

图2 不同传感器节点数目情况下ROC曲线
3 几种特殊情况
3.1 理想信道Pe=0
针对传统的分布式目标检测应用而言,假设传感器节点与融合中心之间信道是理想的,即Pe=0,配置有N个传感器节点的目标融合检测系统未知数个数为2 N+1,方程个数为2N-1,为了求解方程的精确解或近似解,需满足2N-1≥2 N+1,即N≥3。当N=3时,即SN目标检测系统配置有3个传感器节点,未知参数个数为7,方程个数也为7,可以获得未知参数的精确解,在这种情况下,文献[15]给出了详细的论述,在此不再赘述。需要指出的是,相比于文献[15]提出的理想信道情况下在线迭代方法,本文将信道的衰落、噪声干扰考虑到在线迭代决策融合目标检测中,利用每个方程包含相同的平均比特错误率这一特征,从而能够有效地估计出这一参数。
3.2 Neyman-Pearson准则下在线决策融合
Neyman-Pearson准则下,假设传感器节点虚警概率相同,即=(i≠j)。当整个SN目标检测系统采用Neyman-Pearson准则时,假设传感器节点的虚警概率相同且已知。在这种情形下,配置有N个传感器节点的目标融合检测系统未知个数为N个节点的检测概率,H1的出现先验概率为π1,以及非理想信道的Pe,共有N+2个未知数,方程个数为2N-1。当2N-1≥N+2,即N≥3时,仍可获取未知参数θ=[P(H1),Pe,,…,]T的NLS解。
3 仿真结果
为了验证本文提出的非理想信道条件下,基于传感器网络的在线决策融合目标检测方法的收敛性,考虑了一个融合中心和N个传感器节点组成的目标决策融合探测系统,传感器节点与融合中心之间通信信道是有误码的。在仿真实验中,假设局部传感器节点和目标都是二进制源,即输出为0-1组合,其中1的个数服从假设的概率分布。由4个节点和1个融合中心组成的融合系统,并假设概率:

在这些概率假设下,通过蒙特卡罗仿真产生大量的目标、节点0-1输出。在这种蒙特卡罗模拟下,采用本文提出的在线决策融合方法,在线地估计出各个未知参数,进而在融合中心进行决策融合。
图3~图5分别给出了4个传感器节点的检测概率估计,虚警概率估计以及非理想信道平均比特错误概率估计,每次估计进行了100次的平均,以减小NLS估计误差。在运算复杂度方面,仿真实验中我们也给出了特定CPU下单次最小二乘估计方法的运行时间。在Intel Corei5-4200U的CPU,1.6GHz主频下,经过10次平均,单次运行时间约为90.5ms。

图3 传感器节点检测概率的估计

图4 传感器节点虚警概率的估计

图5 平均比特错误率概率的估计
由图3~图5看出,随着迭代次数的增加,局部传感器节点检测概率,虚警概率以及信道平均比特错误概率趋于稳定,经过约为5 000次的迭代收敛到真实概率值。
图6给出了融合中心在虚警概率为PF=0.01时,Neyman-Pearson准则下,检测概率的迭代曲线,并对比了EGC融合统计量在已知检测概率,虚警概率,平均比特错误率情况下的检测性能。由图可以看出,理想信道条件下(Pe=0),LRT的检测性能最优,EGC检测性能略有下降;非理想信道条件下,LRT性能优于EGC性能;同时,在迭代稳定后,已知局部传感器节点先验信息的检测统计量(LRT,EGC)优于通过估计得到的相应检测统计量,即通过迭代估计后,统计量LRT,EGC检测性能略有下降。

图6 最优LRT融合规则,EGC的检测概率随迭代变化曲线
图7描述了LRT,EGC在先验信息已知以及迭代估计条件下ROC曲线,检测性能对比结果与图5相同,相比于已知先验的LRT,EGC统计量,迭代估计的LRT,EGC统计量检测性能稍有下降,再一次说明了本文所提出的基于WSN在线目标检测方法的有效性。

图7 ROC曲线
此外,给出了5个传感器节点和1个融合中心组成融合系统在线估计情况,5个传感器节点虚警概率假设为Pf=[0.1,0.1,0.1,0.05,0.06]T,检测概率为Pd=[0.90,0.88,0.82,0.75,0.90]T,先验概率P(H1)=0.7,非理想信道传输错误概率Pe=0.1。在这样的概率假设下,通过蒙特卡罗仿真产生目标、传感器节点的二进制输出,利用本文构建的模型及求解方法在线地估计出未知的参数。当局部传感器节点决策数为5 000时,经过100次的平均估计,得到如下估计可以看出,经过最小二乘参数估计方法可以得到较好的平均错误概率、H1先验概率以及检测概率估计,但是虚警概率估计效果不佳,这是由于较小的概率需要较多的决策数才能达到相应的概率。当节点决策数增大的8 000时,同样经过100次平均后得到如下估计结果,可以看出,虚警概率概率估计效果优于节点决策数为5 000时情况。
4 结 论
本文研究了基于SN的决策融合目标检测方法,在融合过程中,融合中心在确定最优似然比融合统计量时,需要获取参与融合的每个传感器节点的检测概率、虚警概率以及局部传感器节点与融合中心之间非理想信道的平均比特错误率。但是每个传感器节点传输这些结果到融合中心需要额外地消耗有限的传感器能量资源、有限的信道资源,且在求取平均比特错误率时,需要通过发送训练序列得到其估计,进一步增加了节点资源消耗。因此,本文提出了一种适用于SN在线决策融合的目标检测方法,该方法在融合之前,通过时间平均获取无条件概率,并在线估计出每个传感器节点的检测概率,虚警概率,以及传输信道的平均比特错误率。之后,选取高质量的传感器节点,采用最优的LRT融合统计量进行融合,进而得到最终的判决输出。相比于已知先验的最优似然比检测融合规则,本文提出的基于SN在线决策融合的目标检测方法检测性能相当。
[1]Liu Y,He Y,Li M,et al.Does wireless sensor network scale?A measurement study on GreenOrbs[J].IEEE Trans.on Parallel and Distributed Systems,2013,24(10):1983-1993.
[2]Wang Y,Fu W,Agrawal D P.Gaussian versus uniform distribution for intrusion detection in wireless sensor networks[J].IEEE Trans.on Parallel and Distributed Systems,2013,24(2):342-355.
[3]Yu T C,Lin C C,Chen C C,et al.Wireless sensor networks for indoor air quality monitoring[J].Medical Engineering &Physics,2013,35(2):231-235.
[4]Rezaee A A,Yaghmaee M H,Rahmani A M,et al.HOCA:healthcare aware optimized congestion avoidance and control protocol for wireless sensor networks[J].Journal of Network and Computer Applications,2014,37(1):216-228.
[5]Chen D,Liu Z,Wang L,et al.Natural disaster monitoring with wireless sensor networks:a case study of data-intensive applications upon low-cost scalable systems[J].Mobile Networks and Applications,2013,18(5):651-663.
[6]Gupta M,Shum L V,Bodanese E,et al.Design and evaluation of an adaptive sampling strategy for a wireless air pollution sensor network[C]∥Proc.of the Local Computer Networks(LCN),2011:1003-1010.
[7]Yun M,Bragg D,Arora A,et al.Battle event detection using sensor networks and distributed query processing[C]∥Proc.of the Computer Communications Workshops,2011:750-755.
[8]Wang X,Fu M,Zhang H.Target tracking in wireless sensor networks based on the combination of KF and MLE using distance measurements[J].IEEE Trans.on Mobile Computing,2012,11(4):567-576.
[9]Yan Y S,Wang H Y,Shen X H,et al.Target detection withmulti-sensor networks:a survey[J].Systems Engineering and Electronics,2015,37(3):473-484.(闫永胜,王海燕,申晓红,等.多传感器网络目标检测方法综述[J].系统工程与电子技术,2015,37(3):473-484.)
[10]Ahmadi H R,Vosoughi A,Distributed detection with adaptive topology and nonideal communication channels[J].IEEE Trans.on Signal Processing,2011,59(6):2857-2874.
[11]Chen B,Jiang R,Kasetkasem T,et al.Channel aware decision fusion in wireless sensor networks[J].IEEE Trans.on Signal Processing,2004,52(12):3454-3458.
[12]Niu R,Chen B,Varshney P K.Fusion of decisions transmitted over Rayleigh fading channels in wireless sensor networks[J].IEEE Trans.on Signal Processing,2006,54(3):1018-1027.
[13]Masazade E,Rajagopalan R,Varshney P K,et al.A multiobjective optimization approach to obtain decision thresholds for distributed detection in wireless sensor networks[J].IEEE Trans.on Systems,Man,and Cybernetics,Part B:Cybernetics,2010,40(2):444-457.
[14]Keshtkarjahromi Y,Ansari R,Khokhar A.Energy efficient decentralized detection based on bit-optimal multi-hop transmission in one-dimensional wireless sensor networks[C]∥Proc.of the Wireless Days(WD),2013:1-8.
[15]Mirjalily G,Luo Z Q,Davidson T N,et al.Blind adaptive decision fusion for distributed detection[J].IEEE Trans.on Aerospace and Electronic Systems,2003,39(1):34-52.
[16]Ahmadi H R,Vosoughi A.Impact of wireless channel uncertainty upon distributed detection systems[J].IEEE Trans.on Wireless Communications,2013,12(6):2566-2577.
[17]Kay S M.Fundamentals of statistical signal processing,Volume 2:detection theory[M].Prentice Hall PTR,1998:165-169
[18]Chen B,Jiang R,Kasetkasem T,et al.Channel aware decision fusion in wireless sensor networks[J].IEEE Trans.on Signal Processing,2004,52(12):3454-3458,
[19]Proakis J G,Salehi M.Digital communications[M].5th Ed.New York:McGraw-Hill High Education,2008:160-220.
[20]Yan Y Y,Wang H H,Shen X H,System modeling and performance analysis for remote target detection of small-scale sensor networks[J].Journal of Electronics &Information Technology,2014,36(7):1625-1630.(闫永胜,王海燕,申晓红.小规模传感器网络远程目标探测系统的建模与性能分析[J].电子与信息学报,2014,36(7):1625-1630.)
[21]Coleman T F,Li Y.An interior trust region approach for nonlinear minimization subject to bounds[J].SIAM Journal on optimization,1996,6(2):418-445.
[22]Shearer J M,Wolfe M A.ALGLIB,a simple symbol-manipulation package[J].Communications of the ACM,1985,28(8):820-825.
Online decision fusion method for target detection based on sensor networks
YAN Yong-sheng,WANG Hai-yan,DONG Hai-tao,JIANG Zhe
(School of Marine Science and Technology,Northwestern Polytechnical University,Xi’an 710072,China)
To solve the problem that the fusion center in a sensor network(SN)cannot completely obtain the local detection performance indices,a target detection model based on the SN is established.An online decision fusion method for target detection with the non-ideal channel between local sensors and the fusion center is proposed.This method constructs the model of solving unknown parameters including local false alarm probabilities,local detection probablities and the average bit error probability of the non-ideal transmission channels.The nonlinear least square method is employed to estimate the unknown parameters.In order to maximize the system detection performance,the sensors with high detection performance are chosen to participate in the fusion.The simulation results show that the estimations tend to be with the true local probability values and the average bit error probability.Compared with the optimal likelihood ratio(LR)based fusion rule,the proposed online decision fusion method exhibits only slight performance degradation.
sensor network;target detection;online decision fusion;nonlinear least square
TN 911.72
A
10.3969/j.issn.1001-506X.2015.08.05
闫永胜(1986-),男,博士研究生,主要研究方向为多传感器网络目标检测与定位。
E-mail:ysyan@mail.nwpu.edu.cn
王海燕(1965-),男,教授,博士研究生导师,博士,主要研究方向为现代信号检测与现代信息处理、水声信息感知、水下电子对抗与智能电子系统、水声通信与组网、目标识别与定位跟踪。
E-mail:hywang@nwpu.edu.cn
董海涛(1988-),男,博士研究生,主要研究方向为传感器网络目标跟踪与数据融合。
E-mail:hai3water@126.com
姜 喆(1984-),男,讲师,博士,主要研究方向为水声通信与信道估计。
E-mail:jzh1723@nwpu.edu.cn
1001-506X201508-1741-07
网址:www.sys-ele.com
2014-11-24;
2015-03-17;网络优先出版日期:2015-04-07。
网络优先出版地址:http://www.cnki.net/kcms/detail/11.2422.TN.20150407.1321.003.html
国家自然科学基金(61401364);教育部博士点基金(20136102120013)资助课题

