考虑面内外摆角对电动绳系离轨过程的参数影响分析
翟 光,苏 飞,张景瑞,张 尧
(北京理工大学宇航学院,北京100081)
考虑面内外摆角对电动绳系离轨过程的参数影响分析
翟 光,苏 飞,张景瑞,张 尧
(北京理工大学宇航学院,北京100081)
利用电动绳系实现空间碎片自主离轨有广阔的应用前景。受洛伦兹力矩和重力梯度力矩作用,绳系姿态将在当地垂线附近振荡。首先采用拉格朗日法建立电动绳系面内外姿态动力学模型;随后结合国际地磁场模型,给出洛伦兹力和洛伦兹力矩的计算方法;最后结合姿态动力学模型和高斯摄动方程,建立了电动绳系离轨数值仿真模型,在考虑无摆角、仅有面内摆角、有面内外摆角的条件下,对电动绳系离轨过程进行仿真对比。仿真结果说明,电动绳系姿态振荡对离轨有明显影响,只有考虑绳系姿态,才能精确预测轨道参数的变化。
电动绳系;姿态振荡;离轨控制;轨道参数;动力学建模
0 引 言
空间碎片对在轨航天器的安全产生严重威胁。利用电动绳系使废弃卫星离轨的概念由美国NASA约翰逊太空中心的Joseph P.L首先提出,随后许多国家对电动绳系技术进行了试验和验证[1-4]。电动绳系系统动力学与控制问题一直是该领域内的一个研究重点。文献[5-6]研究了电动绳系轨道机动过程的动力学稳定性问题,在结构优化的基础上提出了解耦控制策略;文献[7-8]基于珠点模型建立了电动绳系系统的动力学和运动学模型;文献[9]在绳系系统动力学模型中引入弹性形变,研究了绳系形变对系统面内运动稳定性的影响;针对电动绳系机动过程振动抑制和时间优化问题,文献[10-13]提出通过调节绳系电流大小和方向实现电动绳系位置保持,同时抑制绳系的振动和完成电动绳系最优轨道转移;文献[14-15]提出两种反馈控制方法来抑制展开阶段与构型保持阶段的振动,并采用有限元方法分析了系统的横向振动规律;当前电动绳系非线性动力学特性及系统离轨速率也是较多学者关注的问题,文献[16-19]基于高斯摄动方程建立了电动绳系纳星系统的轨道摄动模型,通过解耦方式分析了绳系姿态稳定性,并采用分段最优控制策略,缩短了系统的离轨时间;文献[20]建立了电动绳系离轨时间的理论计算模型,并结合第十一代国际地磁场模型进行了仿真验证。
在目前已有文献中,多数学者不考虑绳系姿态对系统离轨速率的影响,直接假设电动绳系稳定在当地垂线方向,以此开展相关建模与分析研究。事实上在不施加控制时,电动绳系在洛伦兹力和重力梯度力作用下与当地垂线方向有面内外夹角且动态变化,因此很多离轨过程的运动特性分析具有一定局限性。本文基于上述研究,建立了电动绳系轨道摄动模型和姿态动力学模型,分析了电动绳系姿态运动特性,在考虑面内外姿态条件下得到更为精确的离轨模型,通过研究轨道参数的变化,说明了考虑面内外姿态的必要性。
1 电动绳系姿态动力学模型
电动绳系系统如图1所示,为简化问题,做如下假设:绳系末端质量均为质点,且与绳系连接点位于末端质量的质心,系统质心与轨道坐标系原点重合,地球重力场为理想中心力场;同时忽略其他轨道摄动因素对系统运动的影响。
建模参考坐标系如图1所示,OXYZ为地心惯性坐标系;OoXoYoZo为轨道坐标系,其原点位于系统质心,Zo轴为地心指向系统质心方向,Xo轴指向系统速度方向,Yo轴由右手螺旋法则确定;ObXbYbZb为本体系,原点Ob固连于系统的质心,Zb轴为系统质心指向大质量块质心方向,Xb轴方向由下式确定:Yb轴则由右手螺旋法则确定。本文主要研究绳系与轨道面位置关系,所以图1中未标出Yo和Yb轴。

面内外摆角α、β定义如图1所示,面内摆角α为绳系在轨道面投影与Zo轴的夹角,面外摆角β则为此投影与绳系的夹角。

图1 电动绳系系统示意图
1.1 系统的动能
本部分采用拉格朗日定理推导系统的动力学模型。如图2所示,任取电动绳系微元dm,由质心定义,系统满足:
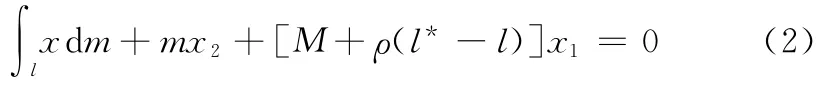
式(2)对于y、z亦成立。式中M和m表示末端大小两质量块质量;ρ为电动绳系的线密度;l*、l为电动绳系总长度和展开长度;x1和x2分别为大质量块和小质量块在轨道坐标系内的x坐标。

图2 电动绳系系统本体坐标系与轨道坐标系
假设L为末端质量指向卫星的矢量(即为绳系矢量),同理由质心定义可得系统质心到末端小质量块和大质量块的矢量L1、L2(其标量l1、l2表示质心到末端质量的绳长)分别为

电动绳系释放过程中,整个系统的动能由3部分组成,系统质心沿轨道运动产生的动能T1;系统绕质心转动产生的动能T2;绳系长度变化产生的动能T3。系统质心绕轨道运动的动能T1表示为



式中,f表示真近点角。同理可得T2和T3的表达式,这里直接给出表达式:
1.2 系统的势能
电动绳系系统任意质量微元dm在重力场中的势能可描述为
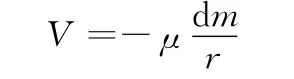
式中,μ为地心引力常数;r为微元到地心距离。
下面分两部分计算系统的势能,其中末端质量的势能为
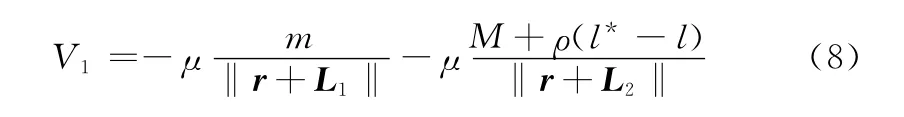
根据两质点在轨道坐标系中的位置关系,对式(8)分母部分进行泰勒展开,并忽略高阶项O(1/r3),则有

式中,i=1,2。将上式代入到式(8)中,由此可以得到末端质量的势能函数

采用同样的方法可以得到电动绳系的势能函数:

考虑绳系在释放过程中发生的弹性变形,引入电动绳系的应变系数ξ,C为电动绳系的弹性模量,A为横截面积,则系统的弹性应变势能可以表示为

根据式(9)~式(11),系统总势能函数可由V=V1+V2+V3计算得到。
1.3 系统的拉格朗日函数
根据拉格朗日定理,系统的拉格朗日函数可表示为

将系统的动能函数和势能函数代入上式可得系统的拉格朗日函数具有以下的形式:

由于模型考虑了连接电动绳系的质量,因此系统的拉格朗日函数和动力学方程变得十分复杂。在实际的工程当中,由于电动绳系质量远小于系统其他部分质量,所以忽略拉格朗日方程中绳系动能和势能;此外,忽略绳系的形变,此时拉格朗日函数中的弹性势能项可略去不计。
根据拉格朗日定理,按式(12)对拉格朗日函数中的广义坐标求导

式中,qj和Qj分别表示广义坐标和广义外力,则可导出系统的姿态动力学方程

定义归一化广义外力

式中,τ(t)和γ(t)分别表示面内摆角和面外摆角方向的外力矩,其为洛伦兹力矩和重力梯度力矩合成。为了提高仿真精度,并便于判断电动绳系系统面内外振动的稳定性,采用无量纲分析,引入无量纲变量:
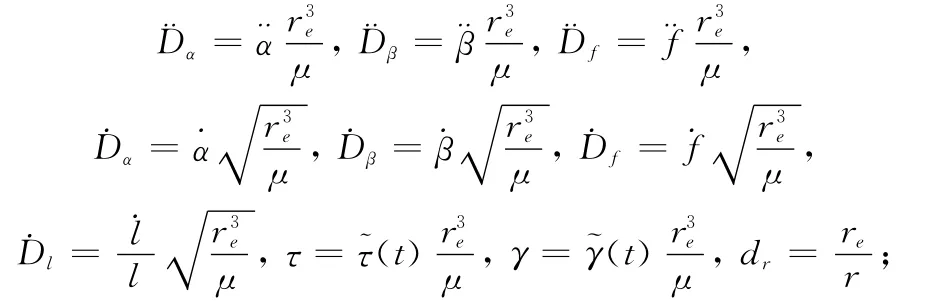
此时方程(14)转换为
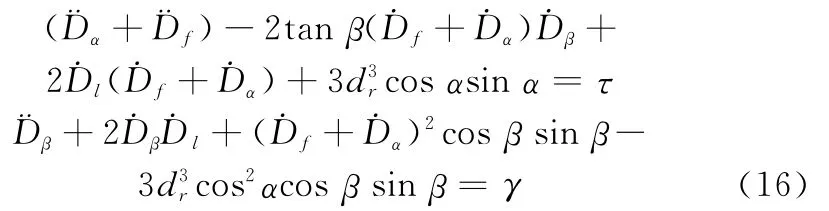
姿态动力学方程(14)是在连接电动绳系刚性假设的情况下推导建立的,而系统的刚性假设只有在连接电动绳系处于张紧状态的时候才能够成立,若电动绳系处于松弛状态时,末端质量之间的动力学耦合关系不再成立,即方程(14)能够描述系统动力学特性的前提条件是连接电动绳系处于张紧状态。
2 摄动力和摄动力矩
2.1 地磁场模型
国际参考地磁场是描述地球主磁场空间结构和时间变化的通用模型。在近地表自由源地区,磁场强度B是一个标量势W的梯度,即

并且该标量势W满足Laplace方程:Δ
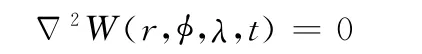
在球坐标系中,Laplace方程的通解为

式中,re为地球参考球赤道半径;r、λ、φ分别为卫星的地心距、经度和地心纬度;、为磁场球谐函数的系数(高斯系数);(sinφ)为n次m阶Schmidt准归一化缔合勒让德函数。
地磁场在地心地固坐标系中可以表示为

式中,eLx、eLy、eLz为东-北-天坐标系三轴单位矢量,此时每个轴上的磁场强度为

本文研究考虑绳系姿态和不考虑姿态的电动绳系离轨特性,建模时应限制磁场模型精度带来的误差,所以取N=10阶地磁场模型,此模型基本考虑了地球主磁场。
2.2 仅有面内摆角的摄动力和力矩
假设绳系的平衡位置落后于当地垂直位置的角度为α,由轨道系x轴、y轴、z轴单位向量eox、eoy、eoz表示绳系长度矢量为

当电动绳系穿过地磁场并切割磁感线,会产生变化的电场E。此时,绳系上的电压、电流表示为

式中,R为绳系电阻,电动绳系系统相对地磁场的速度矢量vr与地球的自转关系为

式中,v、ωe分别为电动绳系系统在轨道系中的速度矢量和地球的自旋角速度矢量,电流在地磁场中的运动感应产生作用于绳系的洛伦兹力为
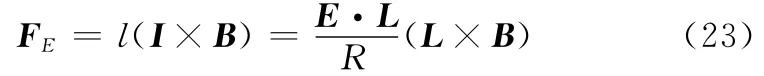
所以作用在绳系上的电动力力矩为
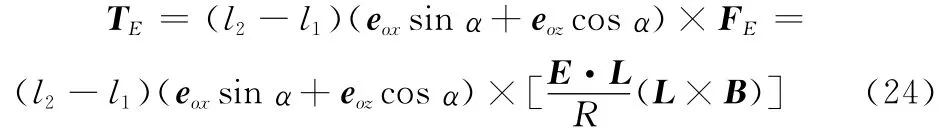
绳系质量mt、末端质量M和m也可以产生梯度力及力矩,假设绳系的横截面积大小一致。则由绳系质量和末端质量和卫星质量产生的梯度力FGt、FGm、FGM分别为

由重力梯度产生的梯度力矩为

2.3 有面内外摆角的摄动力和力矩
电动绳系的面内摆角和面外摆角分别为α和β,则绳系长度矢量在轨道系中可以表示为

电动绳系与当地垂直方向的夹角为

此时绳系上的电压和电流及在地磁场中的运动感应产生的洛伦兹力如式(21)和式(23)。
用虚功原理求解式(15)中的摄动力矩τ(t)、γ(t),把位移微分dL的虚位移用面内外虚摆角δα、δβ[16]表示为

由式(29)得洛伦兹力矩表示为
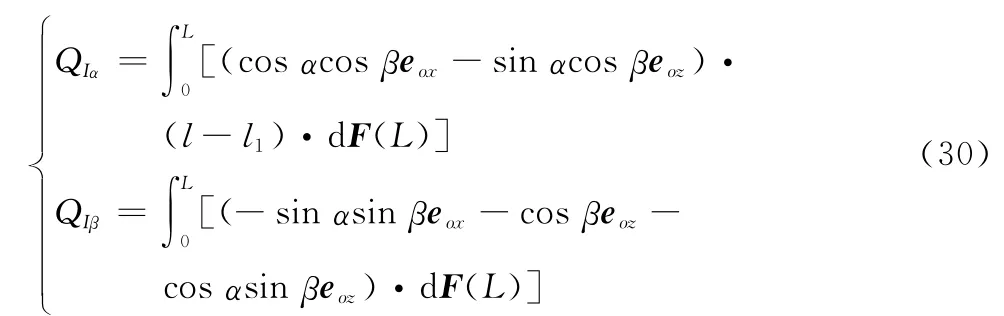
其中,dF(L)=B×ILdL,所以洛伦兹力矩为
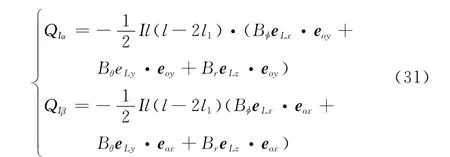
由于M≫m,直接假设系统质心位于大质量块质心处,得洛伦兹力矩为
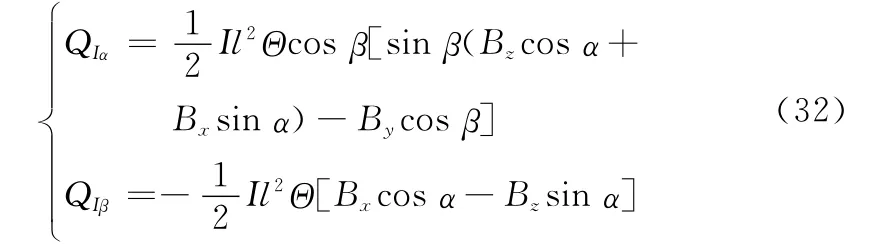
式(32)中

式中,Bx、By、Bz分别为地磁场在轨道系三轴上的分量,代入式(15)即可得到广义力矩。此时重力梯度力矩可按下式计算:
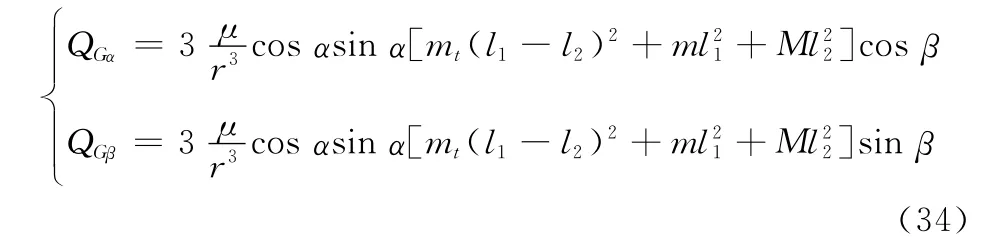
同理可假设电动绳系系统重心位于大质量块处,得到简化的重力梯度力矩。
2.4 轨道运动方程
电动绳系系统在洛伦兹力作用下,轨道发生改变。这里以轨道要素为状态变量描述系统的轨道摄动,建立电动绳系离轨系统高斯轨道摄动方程:

式中,a是轨道半长轴;h是轨道角动量;e是轨道偏心率;u=ω+f;p是轨道半通径;i是轨道倾角;Ω是轨道升交点赤经;ω是近地点幅角;fr、fv、fh分别为航天器位置矢量方向、运动方向和垂直轨道面方向的摄动加速度。
3 考虑绳系姿态的离轨仿真验证
根据上述理论建模与分析的结果,建立电动绳系离轨过程的数值仿真模型,整个仿真模型综合考虑了系统的姿态动力学、轨道摄动、地磁场模型3个部分,研究了电动绳系姿态的变化对系统的各个参数的影响,验证电动绳系的离轨效果。需要说明的是,本仿真模型当中暂未考虑地球形状摄动、大气阻力摄动等因素。电动绳系的参数和绳系轨道初始参数如表1和表2所示。

表1 绳系仿真参数

表2 初始轨道参数
图3是考虑绳系姿态时系统离轨过程地磁场随时间的变化,由于轨道半长轴不断减小,系统位置不断降低,地磁场幅值也不断增大。从图3可以看出其幅值有增大的趋势,这与地磁场的实际情况相符。

图3 EDT所处地磁场矢量变化
为了说明在分析电动绳系离轨过程时,考虑绳系面内外姿态振荡的必要性,本部分分别在考虑和不考虑绳系系统姿态变化的情况下进行了仿真及对比分析,其中绳系姿态变化分为两种情况进行仿真,一种是仅考虑面内的姿态运动,另一种是综合考虑面内外的姿态运动。图4是40h内电动绳系轨道半长轴变化情况,因为是近圆轨道,所以可以用半长轴变化来评价离轨效果。仿真结果说明,在不考虑绳系姿态的情况下,其半长轴减小得最快,同时考虑面内和面外姿态变化时半长轴减小也要比只考虑面内姿态变化时快。若分析长期(2~5个月)降轨,不考虑面内摆角时分析结果误差将更大。所以为了保证离轨模型的准确性,分析电动绳系姿态运动是必要的。

图4 EDT 40h内轨道半长轴变化
图5和图6分别是电动绳系面内角摆角变化曲线和面内姿态运动的相平面图,由图5可看到面内摆角在-0.2rad附近不规则的振荡,由图6进一步可知面内摆角是逐渐收敛的,因此面内姿态运动具有稳定性;图7和图8分别是电动绳系面外摆角变化曲线和面外姿态运动的相平面图,从图可得面外角虽然在0rad附近不规则振荡,面外姿态相轨迹不收敛,但其振荡的幅值是有界的,同时面外姿态会使绳系产生沿轨道半径方向的力,近地点幅角也会随之变化,如图9所示。从图10和图11可知,由于面外角的存在,使洛伦兹力沿轨道面垂线方向的力减小,这使得轨道倾角的变化相对缓慢。
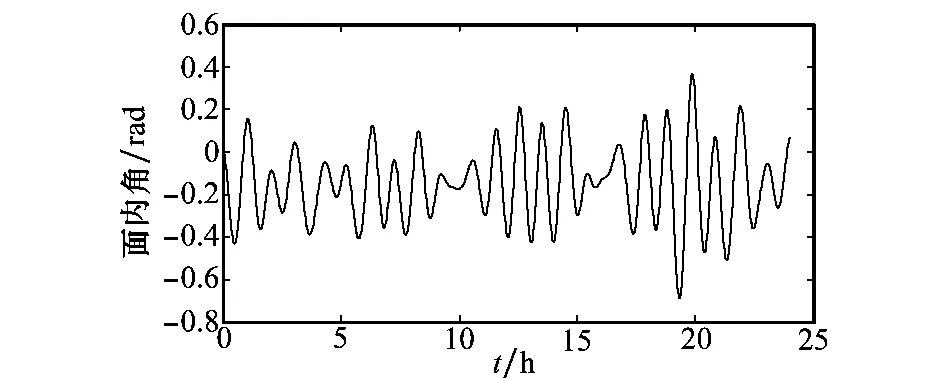
图5 EDT面内姿态角变化
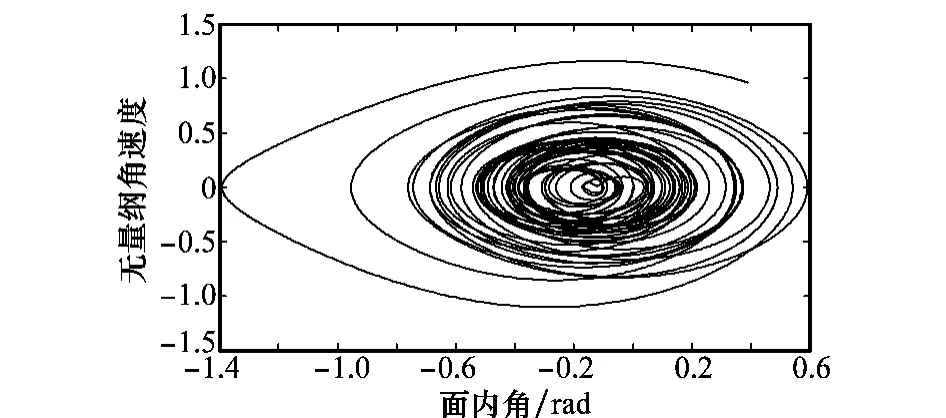
图6 EDT面内姿态相平面
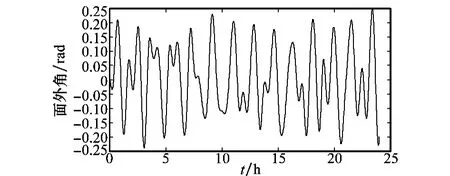
图7 EDT面外姿态角变化

图8 EDT面外姿态相平面

图9 EDT 48h内近地点幅角变化

图10 EDT 24h内轨道倾角变化

图11 EDT 48h点线方向洛伦兹力变化
图12是不同条件下电动绳系离轨过程产生电流的对比,由于面内角和面外角都在稳定在附近振荡,但其上电流幅值变化不大,绳系由此产生的洛伦兹力虽有变化,但仍能实现离轨,由图13可知在综合考虑面内外姿态变化的情况下,洛伦兹力在航天器运动方向的分量最大。

图12 EDT 24h电流变化
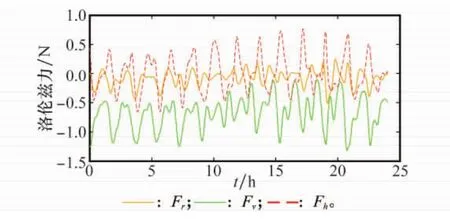
图13 EDT 24h洛伦兹力变化
4 结 论
本文在考虑重力梯度力矩和安培力矩作用条件下,综合分析了电动绳系面内外姿态运动的特性,在此基础上,进一步建立了洛伦兹力作用下的轨道摄动模型,并在考虑电动绳系系统姿态运动的条件下,对系统的离轨过程进行了对比分析。理论建模及数值仿真结果说明,电动绳系系统在轨期间同时存在着面内外姿态振荡,相对于无姿态振荡的情况,其产生的洛伦兹力大小和方向都会发生变化,进而对电动绳系系统的离轨速度产生明显的影响。此外,电动绳系的姿态运动会导致洛伦兹力在轨道平面法向洛伦兹力分量的减小,进而导致离轨过程中轨道倾角变化速度也发生变化。综合上述,电动绳系的姿态运动对系统离轨过程当中的轨道参数变化存在重要影响。因此,为了提高对电动绳系系统离轨过程的预测精度,考虑电动绳系系统的姿态运动是合理且必要的。
[1]Klinkrad H,Beltrami P,Hauptmann S.The ESA space debris mitigation handbook 2002[J].Advances in Space Research,2004,34(5):1251-1259.
[2]National research council.NASA space technology roadmaps and priorities:restoring NASA’s Technological edge and paving the way for a new Era in space[R].Washington D C:National Academies Press,2012:129-130.
[3]Ishige Y,Kawamoto S,Kibe S.Study on electrodynamic tether system for space debris removal[J].Acta Astronautic,2004,55(11):917-929.
[4]Covello F.Application of electrical propulsion for an active debris removal system:a system engineering approach.[J].Advances in Space Research,2012,50(7):918-931.
[5]Mankala K K,Agrawal S K.Equilibrium-to-equilibrium maneuvers of flexible electrodynamic tether in equatorial orbit[J].Journal of Spacecraft and Rockets,2006,43(3):651-658.
[6]Zhang J,Wang F,Li H Y,et al.Reserch on dynamics and control of electrodynamic tether under aerodynamic drag[J].Journal of Astronautics,2014,35(3):291-297.(张健,王峰,李化义,等.气动阻力作用下电动力绳系动力学与控制研究[J].宇航学报,2014,35(3):291-297.)
[7]No T S,Jr C J E.Dynamics and control of a tethered flight vehicle[J].Journal of Guidance,Control,and Dynamics,1995,18(1):66-72.
[8]Banerjee A K.Dynamics of tethered payloads with deployment rate control[J].Journal of Guidance,Control,and Dynamics,1990,13(4):759-762.
[9]Liu L D,Bainum P M.Effect of tether flexibility on the tethered shuttle subsatellite stability and control[J].Journal of Guidance,Control,and Dynamics,1989,12(6):866-873.
[10]Corsi J,Less L.Stability and control of electrodynamic tether for De-orbiting applications[J].Acta Astronautic,2001,48(5):491-501.
[11]Williams P.Optimal orbit transfer with electrodynamic tether[J].Journal of Guidance,Control,and Dynamics,2005,28(2):369-372.
[12]Larsen M B,Blanke M.Passivity-based control of a rigid electrodynamic tether[J].Journal of guidance,Control,and Dynamics,2011,34(1):118-127.
[13]Steven G T,Hakan S.Orbital maneuvering with electrodynamic tethers[J].Journal of Guidance,Control,and Dynamics,2003,26(5):805-810.
[14]Hoyt R.Stabilization of electrodynamic tethers[C]∥Proc.of the AIP Conference,2002:570-577.
[15]Xu D F,Kong X R,Hu C W.Modeling study of transvers vibration in electro dynamic tether[J].Journal of Astronautics,2009,30(2):453-457.(徐大富,孔宪仁,胡长伟,电动力缆绳的横向振动建模研究[J].宇航学报,2009,30(2):453-457.)
[16]Zhong R,Zhu Z H.Dynamics of nanosatellite deorbit by bare electrodynamic tether in low earth orbit[J].Journal of Spacecraft and Rockets,2013,50(3):691-700.
[17]Zhong R,Zhu Z H.Optimal control of nanosatellite fast deorbit using electrodynamic tether[J].Journal of Guidance,Control,and Dynamics,2014,37(4):1182-1194.
[18]Zhong R,Zhu Z H.Long term dynamics and optimal control of nano-satellite deorbit using a short electrodynamic tether[J].Acta Astronautic,2013,52(8):1530-1544.
[19]Sun G H,Zhu Z H.Fractional order tension control for stable and fast tethered satellite retrieval[J].Acta Astronautic,2014,104(1):304-312.
[20]Bombardelli C,Zanutto D,Lorenzini E.Deorbiting performance of tethers in inclined orbit[J].Journal of Guidance,Control,and Dynamics,2013,36(5):1550-1555.
E-mial:gzhai@bit.edu.cn
苏 飞(1990-),男,硕士研究生,主要研究方向为绳系卫星编队动力学与控制。
E-mial:sufeisophy@163.com
张景瑞(1974-),女,教授,主要研究方向为航天器姿态动力学与控制技术。
E-mial:zhangjingrui@bit.edu.cn
张 尧(1985-),男,讲师,主要研究方向为航天器振动抑制控制技术。
E-mial:zhangyao@bit.edu.cn
Analysis of libration impact on the deorbit mission of space electro-dynamic tether
ZHAI Guang,SU Fei,ZHANG Jing-rui,ZHANG Yao
(School of Aerospace and Engineering,Beijing Institute of Technology,Beijing 100081,China)
Using the electro-dynamic tether system for space debris deorbit has a broad application prospect.Under the torque generated by Lorentz force and gravity gradient,the electro-dynamic tether librates along the local vertical.Base on Lagrange principles,the attitude dynamic associated with in and out-of-plan libration is established at first.The international earth’s magnetic model,the Lorentz force and torque are calculated.Finally,by combining the attitude dynamics model and Gauss perturbation equation,the numerical model for electro-dynamic tether deorbit is established,and both the libration and non-libration deorbit mission are simulated,respectively.Simulation results show that the in and out-of-plan libration exist and have an obvious effect on the deorbit system.Only considering the attitude of the electro-dynamic tether system,orbital elements change can be convinced.
electro-dynamic tether system;attitude tracking;deorbit control;orbital elements;dynamics model
TP 24
A
10.3969/j.issn.1001-506X.2015.08.19
翟 光(1979-),男,副教授,主要研究方向为航天器制导、导航与控制技术。
1001-506X201508-1837-07
网址:www.sys-ele.com
2014-07-07;
2014-10-28;网络优先出版日期:2015-01-06。
网络优先出版地址:http://www.cnki.net/kcms/detail/11.2422.TN.20150106.1218.007.html
国家自然科学基金(11102018);国家高技术研究发展计划(863计划)(2013AA7042018)资助课题

