复杂条件下天空图像的增强

聂恺，何秋生

(太原科技大学电子信息工程学院，太原 030024）

复杂条件下天空图像的增强

聂恺，何秋生

(太原科技大学电子信息工程学院，太原 030024）

设计了一种在复杂天气条件下对天空图像的增强方法。针对图像噪声对增强效果的影响，我们利用热核方法对图像进行降噪处理。为了利用热核方法对图像降噪，我们使用无向加权图来表示文中的像素点阵图，由热方程捕获加权图的各向异性扩散，以此保留图像的最大结构信息;我们通过自适应子块局部方差法对平滑过的图像进行增强，结果表明，这种方法可以有效的增强图像效果，对后续的分割等操作提供有利的条件。

齿形轴类件;冷体积成形;塑性成形;成形装备

当对天空中目标进行跟踪，尤其是以太阳为目标时，在对以天空为背景的图像不断采样的过程中，由于大气结构存在规律性弱，难以预测，扰动强烈的因素，给获得的图像造成了诸多影响。其中噪声的增加与图像信息的退化等问题会对图像分割，特征提取，图像识别等后续处理带来很多的困难。进几年来，随着计算机技术的增强，研究人员对相关问题进行了更深入的研究［1-7］。

为了在增强图像的同时排除噪声的影响，常对图像先采用低通滤波处理，最常用的是高斯滤波，这种方法能够有效的消除图像中的噪声问题，但不可避免的会对图像细节造成影响。Perona与Malik在文献［8］中提出了P-M方法来滤除噪声平滑图像，保留图像的边缘信息。Catte等人在文献［9］中对P-M方法提出一种改进方案，之后又出现了基于偏微分方程扩散的多值图像平滑［10］。随着多学科的融合，发现图像的扩散过程可以通过热方程来获得，文献［10］中利用热方程的解——热核，有效的辨识出了图像的边缘信息，在平滑过程中对边缘进行了保护。近期也有一些文章对热核方法做了相应的研究与应用［11-14］。

对于图像的增强，常用全局直方图均衡化算法，其计算简单，但难以反映局部变化。文献［15］中采用的同态滤波算法可以有效的处理光照不均造成的暗影问题，不过计算量较大。文献［16］中采用了局部直方图算法，有效对局部图像进行了增强。文献［17］利用了局部对比度增强的方法，它使得局部的图像细节得到了有效的增强，但无法优化图像的动态范围。文献［18］采用了局部方差法来增强图像，其算法简单，对图像细节进行了有效的保留与增强。

我们针对复杂多变的气候条件，如变化的云层，雾霾，扬沙等，对以太阳为目标的天空图像造成的照度不均，细节退化，噪点增加等问题，利用热核算法平滑图像，同时保持图像结构完整，随后针对图像细节的退化问题，结合局部方差法，对图像的进行增强，给后续的图像处理提供有利条件。

1 图像平滑

1.1 P-M方法

对于一张存在噪声的图像G(x)∶Ω⊂R2→R，图像的整体扩散方程如下:

其中▽为梯度算子，div为散度算子，D为描述在各个方向上扩散比率的扩散率，如果图像的扩散过程是各向同性的，那么D则是一个常数，且对所有方向上的▽u有D=1，因此上述方程将变为:

其中△为拉普拉斯算子。

假设D=g(‖▽u‖)，可以得到各向异性扩散方程:

可以看出图像的梯度幅值有效的控制了扩散系数D.对于g(‖▽u‖)Perona和Malik给出了两种比较经典的选择:

其中k是梯度阈值，式(4)对高对比度图像更为有利，而式(5)更适合处理低对比度图像。可以看出，这种方法比高斯模糊更有利，它可以有效保护边界的锐度与位置。不过阈值k的选取存在一定的难度，不能良好的区分边缘点与噪声点。

1.2 热核平滑

为了能够获得图像的热信息，我们使用无自循环的无向加权图G=(V，E)来表示灰阶图像和彩色图像，其中V={1，…，N}(N=m×n为图像所有像素的个数)为图像的点集合，E⊆V×V表示图像的边缘集合。如果在对应位置的一对像素满足在像素点阵上的连通性要求，那么我们就可以认为这条边缘eij∈E存在，边缘eij的权重用w(i，j)来表示，边缘的权重用来体现热流动通过图像时对它的限制。如果边缘权重w(i，j)的值比较大，那么就意味着热量可以轻松的从点vi流动到点vj，相反，如果w(i，j)的值比较小，那么热量要从点vi流动到点vj就要相对困难，而当权重为零时则表明热量无法沿着边缘流动。

边缘权重的选择会直接影响到在消除噪声的过程中对不连续性的保留程度，文献［19］中采用的权重设定具有较快的计算速度，但对噪声的鲁棒性较差。一个比较有效的方法是利用这个点及其周围的点的灰度来计算，为此，需要将每个像素都用一个包含其周围点的窗口来表示，这个方形窗口的大小为n，使用Pi表示像素i的窗口，窗口Pi的灰度级用向量来表示，因此，两个点i，j之间的相似度可以通过两个窗口与之间的高斯加权欧几里德距离来表示:

这里引入高斯滤波起是为了增强距离对噪声的稳定性。通过式(9)我们可以得到的边缘权重为:

其中X(i)为点i的位置，r为控制图像上两点间局域连通性的距离阈值，υ为对比度系数，其取值范围υ∈［0，1］.

为了对图像能够使用热核方法，就要在图像G中建立加权邻接矩阵W，使得其中元素W(i，j)= w(i，j)，构建度矩阵j)，使用度矩阵与加权邻接矩阵，我们可以计算出拉普拉斯矩阵L=T-W，其形式如下所示:

这个拉普拉斯矩阵的谱分解可以写为L= ΦΛΦT的形式。

与拉普拉斯矩阵L相关的图像热方程的矩阵形式为:

其中t为时间，是控制热扩散率的比例系数，Ht为热核矩阵，L是规范化的图像拉普拉斯矩阵。其解可以利用指数化拉普拉斯矩阵和时间t获得:

由于拉普拉斯矩阵L可以表示为L=ΦΛΦT，那么式(11)变为:

其中热核Ht为对称矩阵。将图像G的点i，j代入可以得到:

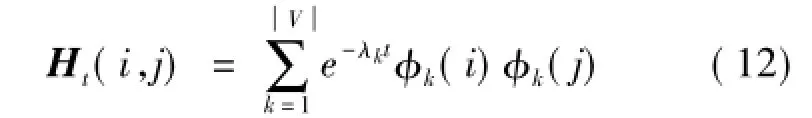
当t趋于0时，存在Ht⋍I-Lt，既热核由图像的局部连通结构决定，由于拉普拉斯矩阵L由图像的局部结构获得，所以可以认为在较短的时间内，热核的值由拉普拉斯矩阵L决定。当t比较大时，存其中λ2为最小非零特征值，φ2为相关特征向量，因此可以看出在大时间条件下，热核的值由图像的全局结构支配。

为了使用扩散过程来平滑图像，需要使得在每个节点间插入的热能等同于相对应点的灰度，随着时间的发展，最初插入到节点之间的热能会通过图像的边缘扩散，而边缘的权重则相当于热导率。热扩散进程由式(12)所示的微分方程决定，初始条件中的热能由对应的点的灰度决定，图像中每个点的灰度转换的列向量C→满足方程:

可以得到在t时刻，平滑图像中j点的灰度为:

对于彩色图像(RGB)，只需要分别处理颜色三条不同的通道即可。

2 图像增强

在对之前平滑处理后的图像进行增强处理，可以很大程度上的还原图像、增强效果，同时避免噪声带来的负面影响。

2.1 直方图均衡化算法

利用直方图均衡化算法来提高图像的对比度是一种常见的方法，其主要分为全局直方图均衡与局部直方图均衡。全局直方图均衡算法计算简单，但存在影响图像基本特征，增强过度，噪声加剧等问题。

直方图修正的目的是为了使得修改后的直方图趋向均匀分布，同时还能够保持原有直方图的特征。当输入图像G的直方图为hi时，存在一个均匀直方图u，使修正后的直方图h接近u，方程如下:

其中λ(λ∈［0，+∞］)为控制对比度增强等级的系数。

在传统直方图均衡化算法中，会对每个灰度级对应的像素个数进行统计，容易受到噪声的影响，因此通过设定阈值r，让每个像素g(x，y)与其前移两列的像素g(x，y-2)做比较，当时对该像素的灰度进行统计，通过对阈值r的设定，一定程度上排除了噪声对直方图均衡化的干扰。

为了扩大图像的动态范围，需要构建如下映射:

其中k*=1/(1+λ)，参数b，w根据图像的最大最小亮度设定，参数α根据图像的对比度设定。但如何有效设定各项参数的以及解决灰度级损失还存在改进的空间。

2.2 局部方差增强法

由于图像细节往往是高频信息，所以通过计算图像局部方差的变化，可以有效分析出图像的细节信息。局部方差增强法的主要原理就是把图像的对比度增强因子定义为以局部方差为变量的函数，然后把对比度增强运算应用到图像的局部区域，从而扩展局部图像的灰度范围，然后遍历整个图像［17］。

首先要对需要定义窗口大小，如果窗口选取的尺寸较小，则其内部可统计到的灰度数有限，对比度拉伸过大，影响效果;若窗口的尺寸较大，虽然可统计到较多的灰度数，但计算量庞大，对比度拉伸过低，增强图像的清晰度作用出现降低。窗口的大小可以通过比较全局图像的标准差:与窗口内局部图像的标准差:来得到。其中窗口的初始大小为w×h，图像的灰度级范围为［0，L-1］，p(fi)为灰度级fi的概率，Eg为全局图像的均值，El为窗口内图像的均值。如果σl＜kσg(k为小于1的常数)，则认为窗口内所包含的灰度数不足，将窗口的长度分别延长一个步长w+a，h+b，重新计算出扩大窗口后的局部标准差σ'l和kσg进行比较;如果＜kσg则继续增大窗口一个步长，直到出现σl＞kσg，如果扩展超出图像的边界则保持超出前的大小。

根据窗口区域内像素的原灰度范围［P，Q］，通过增强因子ε，得到拉伸后的新的灰度范围［P'，Q'］且设定值域在0～255之间，其中ε=D/，D为常数，可以根据不同图像的方差大小来变化。则:

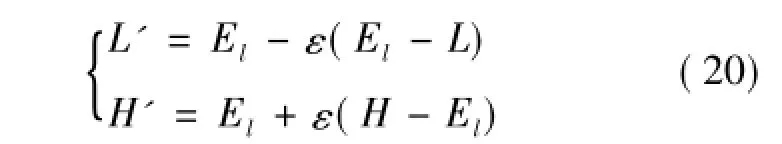
对窗口区域内的中心像素点(i，j)进行等比例灰度变化，使其变化后局部亮度保持基本不变，令g(i，j)为增强后的窗口中心点像素值灰度:

让窗口逐像素位置移动，完成整幅图像的增强。

3 试验结果与分析

在进行平滑处理时，我们将窗口大小定义为5 ×5通过式(7)计算边缘权重，虽然更大的窗口大小可以提供更好的效果，不过也会耗费更多的计算时间。平滑处理效果与三个自由变量相关，分别为式(6)中的σ，式(7)中的k，以及扩散终止时间ts.其中σ的大小由噪声的方差决定，一般选取为零均值噪声标准差大小的一半;k的大小影响热扩散速率，通常设定在0.05-0.15之间;ts的取值由图像需要达到的平滑效果决定，一般取值小于10.在进行图像增强处理时，增强效果受到两个常量的影响。我们将k值定为0.6，较大的k可以提供更好的效果，不过也会加大计算量;D值的大小一般由图像的方差大小来决定，根据图像的方差大小来变化。

图1(a)为一幅典型的天空图像，并受到噪声干扰。分别使用高斯滤波，P-M方法与本文方法进行比较。图1(b)为经过高斯滤波平滑后的图像，图1 (c)为经过高斯滤波处理后100%大小的局部图像，可以看出噪声被有效的消除，但目标的轮廓被明显的模糊了。图1(d)使用了P-M方法进行噪声处理，图1(e)为图1(d)局部100%大小图像，可见边缘被良好保留，但出现了明显的色块问题，平滑效果并不理想。图1(f)是本文算法的平滑效果，其中t=3，k=0.15，σ=0.7，图1(g)为其100%大小的局部图像，可以看出，图像的噪声得到了消除，很好的保持了图像的平滑性，且边缘信息丢失较少，边界明显。图1(h)为t=5，k=0.15，σ=0.7时的效果，可以看出噪声进一步得到消除，不过图像的边缘受到了一定影响，图1(i)为图1(h)的局部100%大小图像。

图1 图像降噪结果比较Fig.1 Illustration of the effectiveness of different noise-decreasing methods

图2 图像增强结果比较Fig.2 Illustration of the effectiveness of different enhancement methods

图2显示的是在利用平滑处理的图像增强结果。图2(a)显示为经过局部直方图均衡化处理的效果，可以看出虽然图像的对比度得到了提升，细节相应加强，但灰度级的损失比较明显，太阳的轮廓被错误拉伸。图2(b)采用了本文所示方法，其中k=0.6，D=0.3，可以看出云层边界相对明显，太阳轮廓得到改善，局部细节有所加强，且图像保持了原有的平滑效果。图2(c)中k=0.6，D=0.5，可以看出对比值更加明显，不过太阳轮廓有一定程度拉伸。

4 结束语

针对复杂条件的天空图像易出现的问题，提出了一种使用热核信息的算法，同时结合局部方差增强法，有效解决了平滑过程中边缘信息的保护问题以及图像增强引起的噪声增加，整体动态范围差的问题，完善了对天空图像采样的预处理，为后续的图像分割，辨识等操作提供了有利的条件。

［1］CODRUTA O ANCUTI，COSMIN ANCUTI AND PHILLIPE BEKAERT.Enhancing by Saliency-guided Decolorization［C］∥IEEE Conference on Computer Vision and Pattern Recognition，2011:257-264.

［2］NARASIMHAN SQNAYAR S K.Contrast restoration of weather degraded images［J］.PAM1，2003，25(6):713-724.

［3］BOUGLEUX S，ELMOATAZ A，MELKEMI M.Local and nonlocal discrete regularization on weighted graphs for image and mesh processing［J］.International Journal of Computer Vision，2009，84(2):220-236.

［4］禹晶，李大鹏，廖庆敏.基于物理模型的快速单幅图像去雾方法［J］.自动化学报，2011，37(2):143-149.

［5］MING JUNG SEOW，VIJAYAN K ASARI.Ratio rule and homomorphic filter for enhancement of digital colour image［J］.Neurocomputing，2006，69(7):954-958

［6］PIZARRO L，MRÁZEK P，DIDAS S，et al.Generalised Nonlocal Image Smoothing［J］.International Journal of Computer Vision，2010，90(1):62-87.

［7］GIBBS R G.New Kalman filter and smoother consistency tests［J］.Automatica，2013，49(10):3141-3144.

［8］PERONA P，MALIK J.Scale-space and edge detection using anisotropic diffusion［J］.IEEE Trans Pattern Anal Mach Intell，1990，12(7):629-639.

［9］CATTÉ F，LIONS P，MOREL J，et al.Image selective smoothing and edge detection by nonlinear diffusion［J］.SIAM J Numer Anal，1992(29):182-193.

［10］XIAO B，WILSON R C，HANCOCK E R.Characterising graphs using the heat kernel［C］∥Proceedings of BMVC，2005.

［11］CHEN Z，KIM P，SONG R.Global heat kernel estimate for relativistic stable processes in exterior open sets［J］.Journal of Functional Analysis，2012，263(2):448-475.

［12］DOBBS D，MELCHER T.Smoothness of heat kernel measures on infinite-dimensional Heisenberg-like groups［J］.Journal of Functional Analysis，2013，264(9):2206-2223.

［13］PATANÉ G，SPAGNUOLO M.Heat diffusion kernel and distance on surface meshes and point sets［J］.Computers＆Graphics，2013，37(6):676-686.

［14］MAO J.Eigenvalue inequalities for the p-Laplacian on a Riemannian manifold and estimates for the heat kernel［J］.Journal de Mathématiques Pures et Appliquées，2014，101(3):372-393.

［15］FABRIZIO RUSSO.An Image Enhancement Technique Combining Sharpening and Noise Reduction［J］.IEEE Transactions on Instrumentation and Measurement，2002，51(4):824-828.

［16］艺书，柳晓鸣，涂雅瑗，等.一种改进的雾天降质图像的清晰化算法［J］.大连海事大学学报，2007，33(3):55-58.

［17］喻欣，张勇，杜庆，等.基于直方图修正的局部对比度增强算法［J］.计算机与数字工程，2011(3):5-8.

［18］刘琬臻，付忠良.基于局部方差改进的超声图像各向异性扩散去噪算法［J］.计算机应用，2013(9):2599-2602.

［19］LI X，HU W，WANG H，et al.Robust object tracking using a spatial pyramid heat kernel structural information representation［J］.Neurocomputing，2010，73(16-18):3179-3190.

Complex Sky Image Enhancement

NIE Kai，HE Qiu-sheng
(School of Electronics Information and Engineering，Taiyuan University of Science and Technology，Taiyuan 030024，China)

A method for enhancing sky image in complex weather condition was presented.In order to eliminate the impact of noise in the processing of enhancement，heat kernel method was used to smooth the image.the image pixel lattice using a weighted undirected graph was presented.The heat equation could capture the anisotropic diffusion across this weighted graph-structure，so it could keep the structural information about the image.Then the local variance method was used，which sub-block could be adaptive to enhance the smoothed image.The results show that the method can effectively enhance the image quality，which made a favorable condition for the next steps of processing sussequent segmentation，etc..

image smoothing，image enhancement，heat equation，heat kernel，anisotropic diffusion，complex sky condition

TP14

A

10.3969/j.issn.1673-2057.2015.03.012

1673-2057(2015)03-0217-06

2014-11-05

山西省高校科技创新项目(20120024);山西省自然科学基金项目(2013011035-2)

聂恺(1987-)，男，硕士，主要研究方向为控制理论与控制工程。