基于迭代学习控制的整流器谐波抑制研究

刘慧娟，于少娟，王成宝，杨琛，马亚运

(1.太原科技大学电子信息工程学院，太原030024;2.国网岢岚县供电公司，山西岢岚 036300）

基于迭代学习控制的整流器谐波抑制研究

刘慧娟1，于少娟1，王成宝1，杨琛1，马亚运2

(1.太原科技大学电子信息工程学院，太原030024;2.国网岢岚县供电公司，山西岢岚 036300）

针对传统整流所带来的电网侧功率因数低和电流波形畸变严重等问题，提出了将迭代学习控制算法应用于整流器中，并设计了迭代学习控制器。通过对PWM整流器的建模与分析，可知开关器件的等效电阻和频率等参数的不确定会使得控制系统的稳态性能变差。仿真结果表明，将迭代学习控制应用于PWM整流器波形控制中，可以有效改善整流器的稳态性能和降低交流侧输入电流谐波畸变率。

PWM整流器;迭代学习控制;复合控制

近年来，电力电子技术发展迅速，将其应用于变流设备所引起的电网谐波污染问题也愈来愈严重。随着全控型器件的出现和发展，将PWM控制技术应用到整流器中，不仅可以提高电网侧功率因数，还可以使能量双向传输。本文首先介绍了单相电压型PWM整流器(Voltage Source Single-phase Rectifier)的工作原理，简称VSSR。然后建立了两种不同的数学模型。一种是在静止坐标系下的数学模型，另一种是在d-q坐标系下的数学模型。研究表明在d-q坐标系下更有利于系统控制器的设计。

本文首先设计了在SPWM调制下的双闭环PI控制系统，但是传统的PI控制不能很好的平衡快速、平稳，精度和稳定性之间的矛盾。由于PWM整流器是一种非线性，强耦合的系统，而迭代学习控制对一些难以建模，强耦合，非线性系统有很好的控制效果，能够实现高精度轨迹跟踪。文献［1］中黄辉将重复控制应用于VSSR中，成功完成了期望轨迹的高精度跟踪。由于重复控制是迭代学习控制的一种特殊情形，它表现在期望轨迹是否具有周期性。为此本文提出了在双闭环PI控制中加入迭代学习控制，构成一种新的控制策略。通过仿真表明，新的复合控制策略能降低交流侧电流谐波畸变率，有效的改善系统的稳态性能。

1 单相PWM整流器数学模型

图中S1～S4是IGBT的开关函数，L是交流侧滤波电感，C是滤波电容，R是综合等效电阻。

图1 VSSR的拓扑结构图Fig.1 Topology structure of VSSR

在正常工作的时候，不考虑H桥交流侧电压UAB和iL中的谐波分量，系统可以简化成图2所示的交流电路，US是电网电压，UR是电阻两端电压，UL电感两端电压，UAB是H桥交流侧电压，iL是流过电感的电流。图2可以用UAB和iL表达为:

式中，US、L、R是固定不变的量，因此调节系统电流的大小和相位就转化成调节UAB的大小和相位［2］。

图2 VSSR的交流电路图Fig.2 AC circuit chart of VSSR

在PWM占空比相同的情况下，双极性调制的VSSR直流电压脉动峰峰值大于单极性调制［3-7］。所以，本文选择单极性调制方式。

1.1 静止坐标系下数学模型

引入开关函数，将A与B之间的线电压用上下桥臂的开关函数来描述，可以得到电感电流和UAB之间的关系。

运用KVL定理得到:

运用KCL定理得到:

结合式(2)、式(3)，可以得到VSSR数学模型的表达式是:

定义整流器的开关函数为S=S1-.由式(4)可以看出，还需要对开关函数进行进一步分析研究。

1.2 d-q坐标系下数学模型

当稳定运行时VSSR的开关函数表达式是S= S1-S3.仅仅考虑它的基波分量，可以得到us、iL、S各分量的分解表达式如下所示:

w为电源电压的频率，ud、uq、id、iq、Sd、Sq是在d-q坐标系下相应的分量。当VSSR处于稳定运行状态时，这些分量都是直流量，将式(5)带入式(4)中得到如下表达式:

通过控制Sd、Sq即可控制id、iq，从而控制iL.

2 单相PWM整流器双闭环PI控制器设计

选用PI双闭环控制策略，本文将迭代学习控制算法加入电压外环。

将迭代学习控制加入双闭环系统，以得到较好的跟踪效果，同时降低交流侧电流谐波畸变率。

由图3可知，分别通过电压调节器和锁相环得到电流值，二者相乘后得到电流瞬时给定值。

2.1 电流内环控制器设计

图3 VSSR双闭环控制图Fig.3 Double closed-loop control chart of VSSR

忽略直流侧电容电压的微小变化，假定其保持恒值不变，由图3可以得到电流内环模型如图4所示。

图4 VSSR电流内环模型图Fig.4 Current inner model of VSSR

图5 VSSR电流内环简化模型图Fig.5 Current simplified model of inner ring of VSSR

2.2 电压外环控制器设计

电压外环模型如图6所示:

图6 电压外环结构图Fig.6 Structure of voltage outer model

Gi(s)是电流内环等效传递函数，把Gi(s)等效成一惯性环节，一般情况下不考虑它的惯性时间常数，认为它是一放大率为1的比例环节，即Gi(s)= 1.将整流桥的传递函数Gidc等效成一个比例环节，即Gidc(s)=1.

通过计算得出iDC可以表示为:

对参数进行整定得到:

3 加入迭代学习算法后控制器设计

3.1 迭代学习控制

迭代学习控制算法适用于非线性，强耦合的不确定性系统，是利用反复不断的迭代修正，达到需要的期望要求［8-9］。

开环迭代时如下所示:

通过对式(10)和(11)的对比研究可以发现开环迭代学习和闭环迭代学习的主要不同表现在误差的修正项上。前者用到的是上一次的误差修正项，而后者用到的是本次的误差修正项。开闭环除了用前一次的控制和跟踪误差外，还用到了本次的跟踪误差，三者经过综合以后，作为本次的输入。闭环学习控制能够很好地抑制系统内部的非线性和不确定性，消除系统所受到的干扰。因此，它得到了广泛的应用［10］。本文采用P型闭环迭代学习控制构成一种复合控制，图7为其结构示意图:

图7 由P型学习律构成的结构图Fig.7 Constituted Structure of P-type learning law

图中G是控制系统的传递函数，Yd(t)是期望轨迹，uk(t)是第k次输入，Yk(t)是第k次输出量，ek(t)为系统输出误差，其中k为迭代学习的次数。

3.2 引入遗忘因子的迭代学习控制算法

在明确了选用闭环P型迭代学习算法后，我们将遗忘因子引入其中，这样做可以对控制器进行滤波，最终达到削弱系统模型的不确定性对系统敛散性影响的效果［11-12］。

此时P型学习算法的一般形式为:

其中β=［0，1］为遗忘因子，Γp(t)为学习增益。

从式(12)可以得出，在引入了遗忘因子β后，当迭代次数逐渐增加时，控制作用就会变得越强［3］。选取式(12)给定的闭环P型迭代学习律，给定任意的初始控制及状态，所得的序列{xk(t)}k≥0，{Yk(t)}k≥0，{uk(t)}k≥0一致收敛到期望值的充分条件为:

式中，ρ(·)表示谱半径［3］。

用MATALB对双闭环系统求解，最终得到D(t)=0，即系统一直收敛。由此可以看出，系统的收敛性与Γp(t)的取值无关。采用反复试凑寻求最优的方法，最终选取Γp(t)为1.6.

4 仿真分析

为了检验加入迭代学习控制算法后，新的复合控制策略是否优于传统的PI控制，搭建了Matlab仿真模型并进行仿真。系统仿真参数为:UDC为500 V，有效值为220 V，电源频率为50 Hz，L=5.5 mH，C=1 500 μF，R=30 Ω，fs为10 kHz;电压外环:Kp= 2.3，Ki=15，电流内环Kp=1，Ki=0.1.

图8表示的是PI控制时的波形，图9表示的是加入迭代学习控制算法后的复合控制波形图。分析以上图形可以得出，无论采用哪一种控制策略，VSSR基本保持单位功率因数运行。

由图8，图9的对比可知，当系统采用双闭环PI控制时，交流输入电流在0.06 s时达到稳定状态，且它的谐波畸变率8.13%.而复合控制时，交流侧电流调节时间变短，在0.045 s达到稳定状态，谐波畸变率3.58%.由此可知，当加入迭代学习控制算法后，复合控制的效果明显优于PI控制。

图8 PI控制时仿真波形Fig.8 Simulation waveforms of PI control

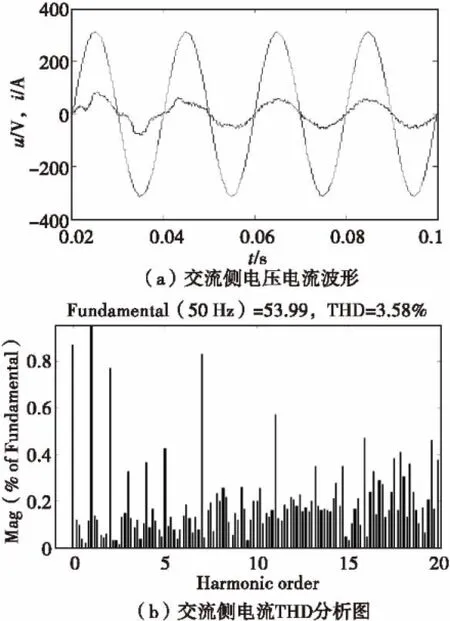
图9 复合控制仿真波形Fig.9 Simulation waveforms of multiple control

5 结论

分析了VSSR的工作原理，构建了它的数学模型，提出了系统的一种复合控制器设计方案。针对传统PI控制存在的快速性与平稳性，精确性与稳定性之间的矛盾，加入了迭代学习控制。仿真结果验证了新的复合控制策略明显优于传统的PI控制。

［1］黄辉.单相PWM整流器控制策略研究［D］.武汉:华中科技大学，2012.

［2］张崇巍，张兴.PWM整流器及其控制［M］.北京:机械工业出版社，2003.

［3］韩刚，蔡旭，王晗，等.基于LCL滤波的PWM整流器稳定性控制的研究［J］.电力电子技术，2011，45(6):79-81.

［4］KESSAL A，LAZHAR R，GAUBERT JP，et al.Analysis and design of an Isolated Single-phase Power Factor Corrector with a Fast Regulation［J］.Electric Power Systems Research，2011，81(9):1825-1831.

［5］WU ZHENXING，ZOU YUNPING.A Performance Improvement Technique for Single-phase PWM Rectifier［C］∥Power Electronics and Motion Control Conference，China，Wahan，2009:1638-1642.

［6］张晓华，郭源博，佟雷.三相PWM整流器的dSPACE实时仿真与控制器参数整定［J］.电工技术学报，2013，28(2): 221-223.

［7］贺博.单相PWM整流器的研究［D］.武汉:华中科技大学，2012.

［8］于少娟，齐向东，吴聚华.迭代学习控制理论及应用［M］.北京:机械工业出版社，2005.

［9］晏静文，侯忠生.学习增强型PI控制系统的收敛性分析［J］.控制理论与应用，2010，27(6):761-768.

［10］黄嘉鹏，杨华云，贺强.基于d，q坐标系单相三电平PWM整流器研究［J］.电力电子技术，2013，47(6):23-24.

［11］兖文宇，于少娟，郭志坚.SPWM逆变器复合控制策略研究［J］.太原科技大学学报，2013，34(6):411-412.

［12］宋可荐.单相三电平PWM整流器控制策略研究［D］.北京:北京交通大学，2012.

Rectifier Harmonic Suppression Based on Iterative Learning Control

LIU Hui-juan1，YU Shao-juan1，WANG Chen-bao1，YANG Chen1，MA Ya-yun2
(1.School of Electronic Information Engineering，Taiyuan University of Science and Technology，Taiyuan 030024，China;2.State Grid Kelan Power Supply Company，Shanxi Kelan 036300，China)

As the low power factor，serious current distortion and other issues to the grid side brought by traditional rectifier，the iterative learning control algorithm was put forward to be applied to PWM Rectifier，and the iterative learning controller was designed.Through the modeling and analysis of PWM rectifier，we can find that the uncertainty of equivalent resistance，frequency and other parameters of switching device will make the steady-state performance of control system poor.From the simulation results，we can find that the application of iterative learning control to PWM rectifier waveform control can improve the static behavior and reduce the input current harmonic distortion of AC side of rectifier effectively.

PWM rectifier，iterative learning control，compound control

TM461

A

10.3969/j.issn.1673-2057.2015.03.006

1673-2057(2015)03-0189-05

2014-11-17

太原科技大学校博科技研究启动资金(20122033);山西省高校教改项目(J2011130，J2013064);同洲电子科技创新基金(TZ201323);省UIT项目(2014287)

刘慧娟(1988-)，女，硕士研究生，主要研究方向为现代控制理论在电气传动中的应用;通讯作者:于少娟，教授，E-mail:yushao71@yeah.net