花键冷敲成形本构关系研究

卢泓昱，刘志奇，，宋建丽，李永堂

(1.太原科技大学机械工程学院，太原 030024；2.金属材料成形理论与技术山西省重点实验室，太原 030024）

花键冷敲成形本构关系研究

卢泓昱1，刘志奇1，2，宋建丽2，李永堂2

(1.太原科技大学机械工程学院，太原 030024；2.金属材料成形理论与技术山西省重点实验室，太原 030024）

花键冷敲成形归结于材料的动态塑性变形过程，为了研究该过程材料动态响应特性，对三种常用冲击载荷下材料本构模型进行理论解析，并根据花键冷敲成形工艺参数对JC本构模型进行修正改进;通过三种本构模型在不同应变率和温度条件下的应力情况，使用流动应力预测值和实验值之差来评估模型误差值。最终结合成形过程物理机制、工艺参数和误差对比，结果表明:在大范围应变率和温度条件下，各本构模型均有其在一定范围内的适用性和精度，但对于花键成形应变率和温度范围内，PTW模型的误差率最小，能够较好预测金属流动应力。

花键;冷敲;本构

花键高速冷敲成形技术是一种制造高精度高性能零件的先进技术，其成形过程是滚打轮绕主轴高速旋转断续敲打工件，同时工件分度旋转最终经过多道次塑性变形形成齿形。该过程中，滚打轮在极短的时间内将能量传递给工件，工件材料受滚打轮轮廓强力挤压迫使材料向齿顶流动，因此工件局部发生大变形并伴随着能量的转化，这种短暂的接触引起材料局部高应变率，高温，高压等物理特性。考虑到冲击载荷下金属材料的物理特性与准静态下有很大差异，因此采用理论解析与试验方法研究本构关系对揭示花键冷敲成形过程材料流动规律有极为重要意义。

现已有许多学者提出若干冲击载荷下金属塑性变形本构关系，但各从不同角度分析;Johnson和Cook提出的JC模型主要是考虑到应变率硬化效应和温度软化效应，对大量实验数据进行拟合的纯经验公式，由于其参数容易获得，因而广泛应用于高率变形的数值模拟。Steinberg-Guinan是一个半经验模型，只考虑到高应变率情况下应变率饱和效应，该模型主要考虑到高压情况下压力和温度在剪切模量中相互耦合对屈服应力影响。后来一些学者对其增加了热激活一项，该项考虑到应变率和温度效应。修正后的Steinberg-Lund增加了其适用范围。PTW模型是Preston，Tonks和Wallace在考虑到强势震荡下，非线性位错拖曳效应占主要作用而提出的本构模型。虽然许多学者已经对不同变形率范围进行试验与理论相结合研究，但系统的从微观机制到宏观理论尚未完成，因此在实际工程应用中必须要选择符合客观物理过程的本构模型，并进行适当修正以期达到数值模拟精度。

1 本构模型

近年来不少学者对金属材料动态力学特性进行了研究，但关于完整的材料塑性物理理论还很缺乏，需要对实验数据分析又得借助理论进行推敲才能得到理想的本构模型。因此，为了研究花键冷敲成形过程中金属流动规律，我们有必要对几个重要的本构关系进行理论分析。

1.1 JC模型

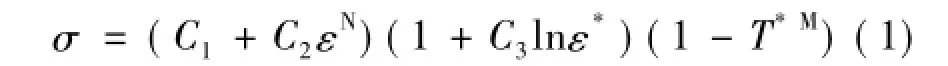
JC强度模型提出于1983年，它可以表示如下:其中σ表示等效屈服强度，ε是等效塑性应变，ε*是无量纲等效塑性应变率。ci，N和M分别是经验系数和经验指数。约化温度:

其中Tr为参考温度(一般取为室温)，而Tm为常态下材料的融化温度。

由于工艺要求的不同，花键冷敲成形过程工件变形速率在102～104s-1之间不等，而在这个过程中材料变形机制会发生变化。许多延性金属在应变率大于103s-1时，表现出现屈服应力巨幅增长现象。该现象归因于位错滑移机制向位错拖曳转变。由于JC模型不能描述这一高应变率敏感性，Rule［1］等人对该模型前两项进行了修正，即:

式中(C5-ln˙ε*)-1这项提高了应变率的敏感性，其中C5是临界应变率水平自然对数，当应变率达到这一临界水平，该项趋于无穷大;但是可以看到应变率敏感性长期增长的贡献归因于1/C5这一项。修改后的JC模型解决了应变率在103s-1时屈服应力巨幅增长这一现象。鉴于JC本构模型是根据三个影响流动应力的物理参数乘积关系拟合出来的，我们可以在其基础上进行修正以满足我们的工程应用。

在实际花键冷敲制造中，滚打轮绕主轴高速旋转，由于极高的转速和瞬间的工间接触，这会产生极高的压强，因此我们可以将其考虑为影响材料屈服应力因素之一，这样我们可以引入压力强化因子f(P)，即可得:

式中:f(P)为压力强化函数，根据压力变化情况，我们可以设定强化函数:

如f(P)=1+αP+βP2;α、β为压力硬化参数。

考虑到花键冷敲过程往往会有大量循环流动的冷却液与润滑剂，工件敲击一次产生的热会被冷却液立即带走，所以温度软化效应没有那么明显，因此主要影响材料屈服应力主要因素是应变程度、应变率和压力强化;对于参数m的选取应该适当增大，于是在改进的模型基础上我们可以根据实验数据通过Matlab软件计算出模型中的各个参数。

1.2 SL模型

金属材料在冲击载荷下伴有高温、高压和高应变率等众多物理因素，实验表明，高应变率下材料的剪切模量是温度和压力的函数。而在准静态情况下一般把剪切变形应力应变看做线性关系，即剪切模量为常数。JC模型对此也是一样的做法。而在Steinberg模型中考虑到温度和压力在剪切模量中的相互耦合，因此在SG模型中剪切力与剪切应变是非线性关系。Steinberg-Guinan-Lund［2］是根据热激活和拖曳所主导的位错动力学，考虑到各向同性应变硬化，热软化，应变率依赖性和压力依赖性对屈服强度所提出的。并且在该模型中，剪切模量与温度和压力是相关联的。在SL模型中屈服强度定义为:

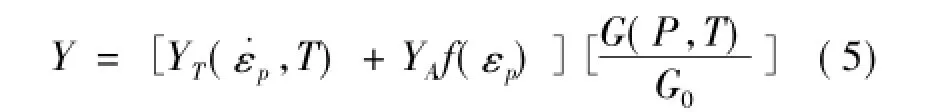
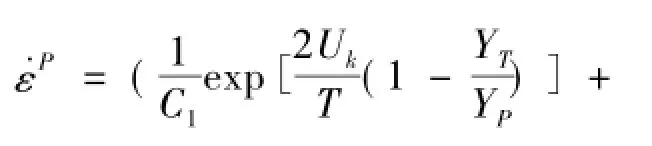
SL模型可用于应变率范围在104s-1～106s-1内的金属塑性变形，该模型联系微观机制和宏观性能，较好的描述了位错运动机制这一转变，即热激活机制向声子拖曳机制转变。

1.3 PTW模型

PTW［3-4］本构模型是Preston，Tonks和Wallace考虑到热激活位错动力学和非线性位错拖曳效应提出的;位错热激活机制对变形的应变率弱势震荡显著影响最高速率为105s-1，在爆炸驱动变形或在高速冲击下有时比105s-1高的多，而且塑性本构模型仅基于热激活机制可能导致显著错误。为了准确描述应变率高达1012s-1下的材料行为，Preston等人在考虑强势震荡机制下的非线性位错拖曳效应提出了一种塑性本构模型;该模型如下:

其中材料常数s0和s∞分别是在零温和非常高的温度的值。κ和γ是无量纲的材料常数。T的换算定义为=T/Tm，其中T是温度，Tm是熔化温度。参数定义为:

PTW模型是迄今为止最全面的本构模型，它可以描述跨越15个量级的金属塑性变形，这源于其建立在正确的物理概念上［5］。即该本构模型分为三个区域;即低率区(热激发的位错滑动)，该区域应变率范围为10-4～104s-1之间，在该区域内对于给定的应变率和温度，无量纲应力总在屈服应力和饱和应力之间。超高速冲击区域(应变率在109～1012s-1之间)，该区域是强冲击波下的本构行为，可采用Wallace理论确定。第三部分为低应变率到高应变率的过渡(105～109s-1).Preston等人用该模型精确预测了铜在应变率103s-1处的流动应力和之后的增长［6-12］。

2 三种流动应力模型误差评估

我们讨论了三种常用的本构模型，但具体选用哪种模型能够得到良好预测结果是需要我们做出误差评价的，为此我们使用流动应力预测值与实验值之差来度量各种应力模型。计算误差公式为:

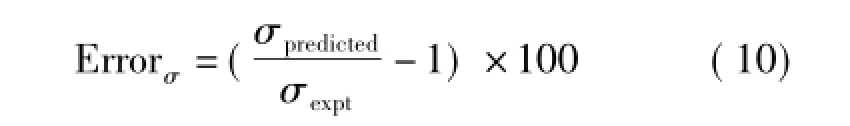
关于一维应力实验下的预测应力与真实应力详细讨论可在一些地方查找到。本文中我们用统计形式总结了预测应力与真实应力之差，表1和表2中的统计信息都是只有真实应变大于0.1获取的，我们可以通过概括表格里多个信息只考虑单一度量进一步简化我们的评估，表3即为根据一个简化的误差度量比较，我们称这一指标为平均最大绝对值(MA)，最大绝对值(MA)被定义为绝对平均误差与标准偏差之和。

花键冷敲成形过程接触区域温度较高，可达到800 K［13］，应变率在102～104s-1之间;由表一看出JC模型和PTW模型在较大温度和应变率范围内均具有较好的精度，误差较小，而SL在低应变率区误差较大，最大误差达到440%.在低温高应变率区，SL相比表现出较好精度，最大误差-12%，而PTW模型最大误差大-29%.JC模型与PTW模型在温度102K～103K，应变率102～104s-1范围内均具有较好的精度，但是相比而言，PTW误差更小即-5%.表二可以看出在应变率较高时，SL表现出优秀的精度，而JC模型误差较大;此时PTW模型和SL模型误差较小。从表三我们可以看出对所有测试最小平均MA是PTW模型即17%，而最大平均MA为SL模型即64%，在大范围应变率和温度范围内PTW模型表现的最好，SL模型最差。如果我们只考虑拉力测试，我们看到JC模型最差，平均MA为25%;对于压缩测试，PTW模型精度最好，只有10%误差，而SL误差为126%.对于高应变率测试与低应变率测试预测结果最好的PTW.花键冷敲成形过程中，滚打轮与工件接触瞬间，滚打轮挤压齿根材料向齿顶流动，因此工件材料主要受滚打轮挤压而发生塑性变形，由以上表格数据看出在花键成形工艺参数条件下，PTW无论在哪项评估中都体现出优越的结果。

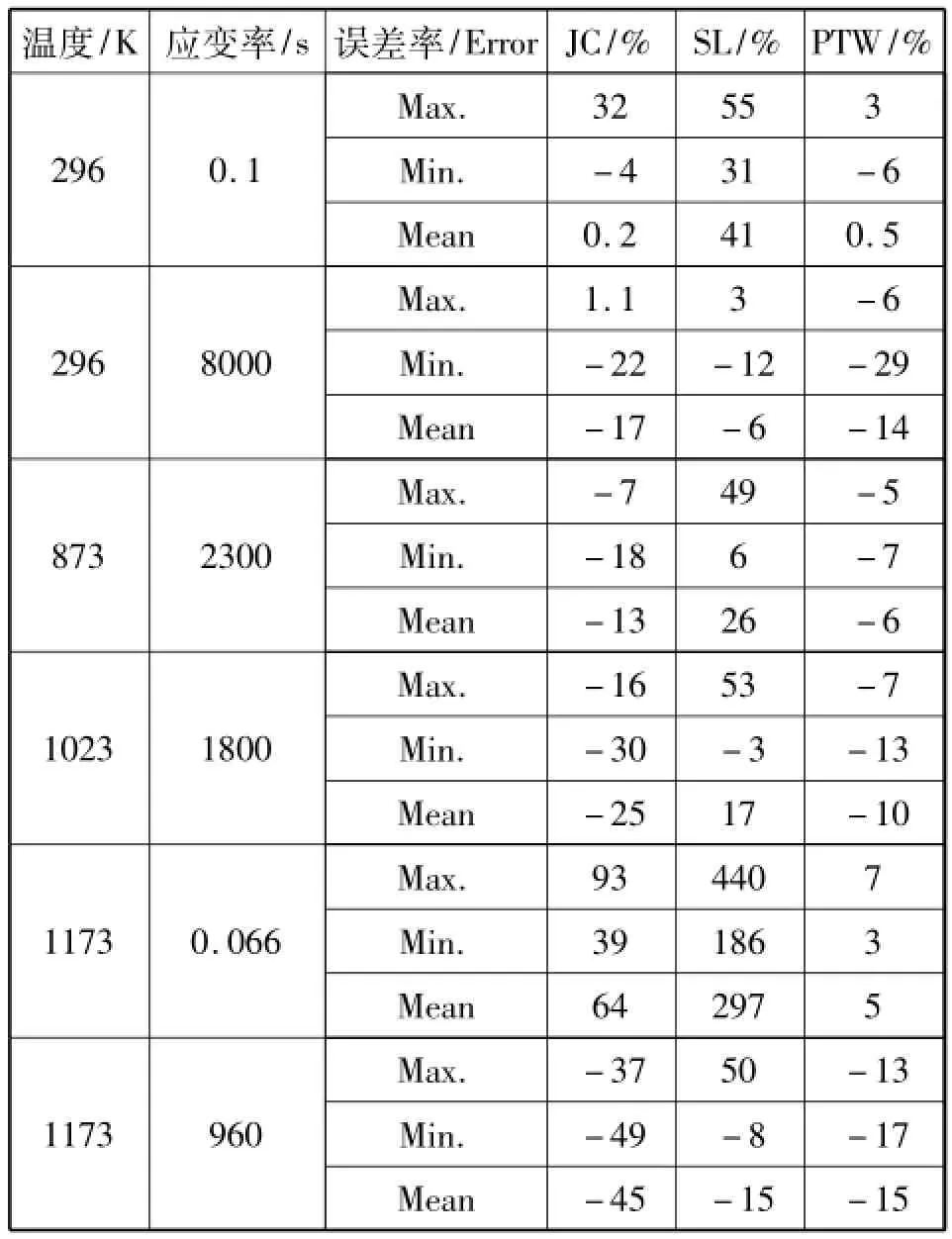
表1 三种本构模型在不同应变率和温度下的预测流动应力误差比较Tab.1 Three constitutive models to predict flow stress error under different strain rate and temperature

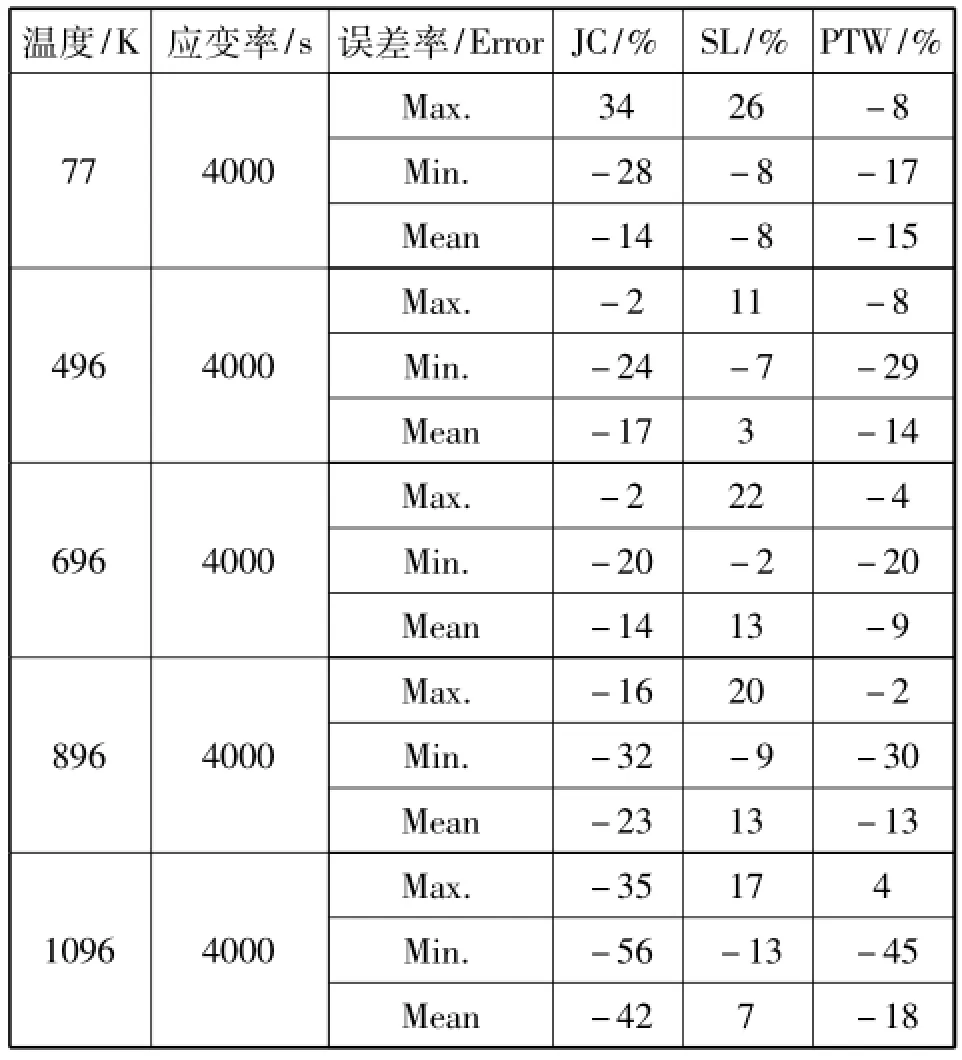
表2 三种不同本构模型在不同温度同一应变率下的预测流动应力误差比较Tab.2 The comparison of three different constitutive models to predict flow stress errors at different temperature and the same strain rate

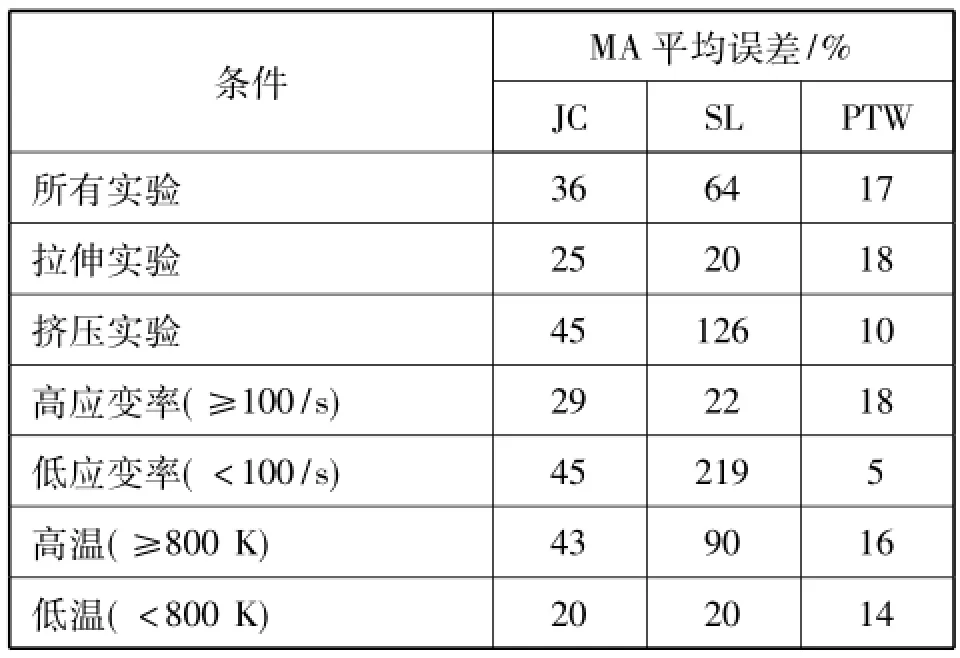
表3 三种本构模型在不同条件下的预测流动应力平均最大绝对误差(MA)比较Tab.3 The comparison of average maximum absolute error of three constitutive models to prediction flow stress(MA) under different conditions

3 结论

(1)现有模型的比较分析是对冲击载荷下金属塑性变形机制的深入理解，这对塑性变形数值模拟时合理选取本构模型提供重要理论依据。本文的工作比较三个知名且应用较广的强载荷下本构模型预测能力，并对其进行修正选用。JC模型适用于范围为104s-1应变率以内，而SL模型将范围扩展到10-4～105s-1以上，该模型具有一定的物理学基础。PTW模型引入了饱和应力，综合考虑了高温、高压、高应变率的影响，并且该本构模型还包含了一个与密度、温度相关的剪切模量的模型，具有空前的适用范围。

(2)一般情况下，应变速率低于104s-1是热激活位错运动起主要作用。在更高应变率109～1012s-1，流动应力是由生子拖曳所支配，这是移动声子位错所需压力，并没有太大的硬化与此过程相关。花键冷敲成形过程中随着主轴转速的不同，成形应变率在102～104s-1之间变化，温度能够达到800 K，变形机制主要是热激活位错运动;我们根据数理统计结果对三种本构模型进行评估，结果是在此区间PTW本构模型误差最小，各项指标最为优越。

(3)Abaqus/Explicit为显式分析求解器，适用于模拟短暂、瞬时的动态事件，求解冲击和其他高度不连续问题，拥有广泛的单元类型和材料模型，以及支持应力/位移分析、瞬态温度/位移分析和复杂非线性耦合物理场分析。ABAQUS为用户提供了强大又灵活的用户子程序接口(User Subroutine)，允许用户在找不到合适模型情况下自定义符合自己问题的本构模型。这样我们可以将利用用户子程序端口对选用适合自己的本构模型进行编程调用，以期得到良好的模拟结果。

［1］RULE W K，JONES S E.A revised form for Johnson-Cook strength model［J］.Int J Impact Eng，1998，21(8):609-624.

［2］STEINBERG D J，LUND C M.A constitutive model for strain rates from 10-4to 106s-1［J］.J Appl Phys，1989，65(4): 1528-1533.

［3］STEINBERG D J，SHARP R.Interpretation of shock wave data for beryllium and uranium with an elastic-viscoplastic constitutive model［J］.J Appl Phys，1981，52:5072-5083.

［4］KIM J B，SHIN H.Comparison of plasticity models for tantalum and a modification of the PTW model for wide ranges of strain，strain rate，and temperature［J］.International Journal of Impact Engineering，2009，36(5):746-753.

［5］刘旭红，黄西成，陈裕泽，等.强动载荷下金属材料塑性变形本构模型评述［J］.力学进展，2007(3):361-374.

［6］侯日立.高温高压环境下金属材料的本构关系研究［D］.武汉理工大学，2010.

［7］李茂生，陈栋泉.高温高压下材料的本构模型［J］.高压物理学报，2001(1):24-31.

［8］彭建祥.Johnson-Cook本构模型和Steinberg本构模型的比较研究［D］.中国工程物理研究院，2006.

［9］JOHNSON G R，COOK W H.A constitutive model and data for metals subjected to large strains，high strain rates and high temperatures［C］∥Proceedings of the 7th International Symposium on Ballistics，1983，21:541-547.

［10］KOCKS U F.Realistic constitutive relations for metal plasticity［J］.Materials Science and Engineering，2001，317(1-2): 181-187.

［11］SAMANTARAY D.A comparative study on Johnson Cook，modified Zerilli-Armstrong and Arrhenius-type constitutive models to predict elevated temperature flow behaviour in modified 9Cr-1Mo steel［J］.Computational Materials Science，2009，47(2): 568-576.

［12］PRESTON D L，TONKS D L，WALLACE D C.Model of plastic deformation for extreme loading conditions［J］.J Appl Phys，2003，93(1):211-220.

［13］张丰收，姚海波，崔凤奎，等.40Cr调质钢高速冷滚打热力耦合数值模拟［J］.机械工程材料，2014(8):101-107.

Study of Constitutive Relation in Cold rRolling Spline

LU Hong-yu1，LIU Zhi-qi1，2，SONG Jian-li2，LI Yong-tang2
(1.School of Mechanical and Electronic Engineering，Taiyuan University of Science and Technology，Taiyuan 030024，China;2.Shanxi Key Laboratory of Metallic Materials Forming Theory and Technology，Taiyuan 030024，China)

The process of spline cold rolling attributes to the dynamic plastic deformation of materials.In order to study the dynamic response characteristics of material，three constitutive model under impact load were analyzed，and the JC constitutive model was amended based on the parameters of spline cold rolling.The error value was evaluated by using the difference of the predicted flow stress and experimental values of material under different strainrate and temperature conditions.Ultimately，by combining the physical mechanisms，parameters of forming and error contrast，the results show that each constitutive model has its applicability and accuracy within a certain range in the large range of strain rate and temperature conditions，however，the PTW model has the minimum error in the range of strain rate and temperature of spline cold rolling，and the flow stress is predicted to be better.

spline，cold rolling，constitutive

TH16，TG393

A

10.3969/j.issn.1673-2057.2015.03.005

1673-2057(2015)03-0184-06

2015-01-20

国家自然基金资助项目(51275331);高等学校博士学科点专项科研基金(20131415110001);山西省自然科学基金(2013011022-1)

卢泓昱(1989-)，男，硕士研究生，主要研究方向为先进制造技术。