并联式串级时滞过程的二自由度Smith预估控制

马文廷，张井岗，赵志诚，秦娜娜

(太原科技大学电子信息工程学院，太原 030024)

并联式串级时滞过程的二自由度Smith预估控制

马文廷，张井岗，赵志诚，秦娜娜

(太原科技大学电子信息工程学院，太原 030024)

针对时滞过程提出一种改进的并联式串级控制结构，副回路采用改进的内反馈控制结构;能够有效的去除副控制器对主回路的影响，从而简化了主控制器的设计。主回路采用改进二自由度Smith预估控制，使主回路的跟踪特性和干扰抑制特性实现解耦;通过对控制器进行设计，能有效地抑制被控过程参数变化和干扰对系统性能的影响，同时保证系统具有良好的鲁棒性。这种新型并联式串级控制方法克服了常规并联式串级控制系统的不足，而且控制算法简单，便于实际系统应用。理论分析和仿真结果表明了这种方法的有效性。

并联式串级控制;内反馈控制结构;Smith预估控制;二自由度控制

串级控制系统能很快抑制进入副回路的扰动，提高控制品质.同时，它能屏蔽副对象(包括控制阀)的非线性.但传统的串级控制系统中也存在不足，例如，主、副回路的振荡、整定参数多、对大的纯滞后对象控制效果不好等.因此，我们研究了并行串级控制系统，系统的结构虽然和串级控制系统类似，但是它们的构筑思想和串级控制系统有很大差别，这对提高系统的控制品质有很大帮助。串联式串级控制系统主要关注主回路的输出特性，而并联式串级控制系统除了抑制扰动对系统的影响外，还考虑了副回路的输出，主要用于某些精馏塔和化学反应器的控制系统。近年来，各国的研究人员对其进行了研究，文献[1]讨论了主、副控制器可调参数在不同的取值域内，控制器的设计形式。研究不够深入。文献[2]副回路采用传统的内模控制，主回路采用时滞补偿的方法，虽然能有效的解决时滞问题，但其控制结构属于一自由度控制，不能实现设定值跟随特性和干扰抑制特性同时达到理想的控制效果。文献[3]提出了一种改进的并联串级控制结构，主回路采用了Smith预估控制，控制器的设计采用了幅频裕度的整定方法，运算量大，效果也不是很好。文献[4]采用分析的方法设计主、副PID控制器，控制结构采用传统的内模控制。控制方法简单，但副控制器包含在主回路中，因而主控制器设计时必须考虑副控制器的影响，造成主回路的等效过程阶次升高，不易于主控制器的设计。

针对上述研究中出现的问题做了进一步的改善，提出并联式串级二自由度Smith预估控制，副回路采用内反馈控制结构，能够有效的解决副控制器对主回路的影响，主回路采用二自由度Smith预估控制结构，实现了设定值跟随特性和干扰抑制特性的解耦，使主回路和副回路的两种特性可以独立的调整。

1 并联式串级二自由度Smith预估控制结构

并联式串级控制系统方块图如图1所示，是一个单输入，双输出系统，系统具有主、副环，但是副变量不作为主对象的输入，主、副对象是“并联的”。

其中，副回路采用内反馈控制结构，r2、d2和y2分别为副回路设定值输入、干扰信号、输出信号;C2为副控制器;Gp2为副过程，Gp2m是副过程模型;GL2为副回路干扰通道模型。主回路采用二自由度Smith预估控制结构，r1、d1、y1分别为主回路设定值输入、干扰信号、输出信号; C1为主回路设定值跟随控制器;Q为主回路干扰抑制控制器;Gp1为主过程;Gm为主过程模型，Gm0是Gm中不含时滞部分;GL1为主回路干扰通道模型。

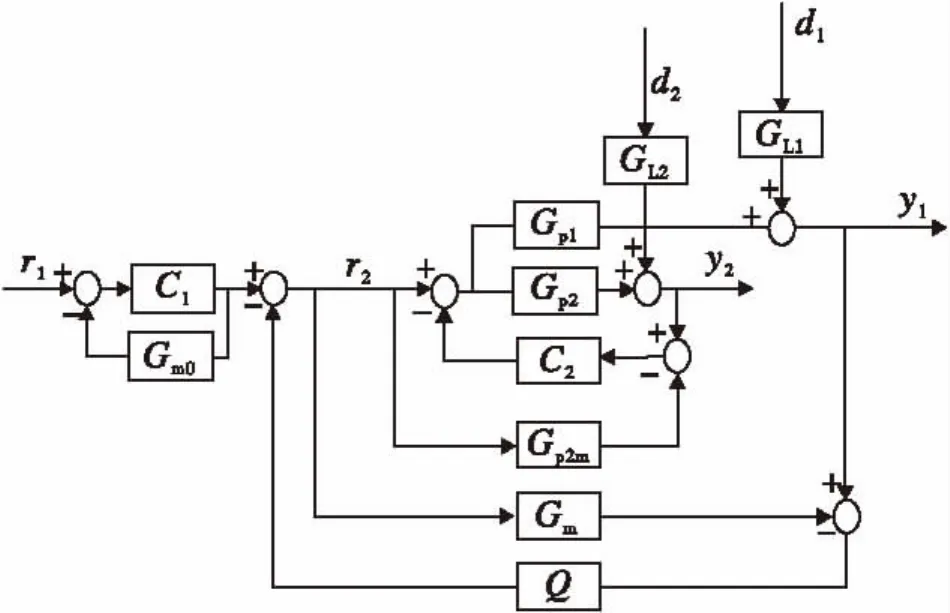
图1 并联式串级二自由度Smith预估控制结构图Fig.1 Parallel cascade 2-DOF smith predictor control structure

由图1可知，副回路的设定值跟随特性和干扰抑制特性分别为:

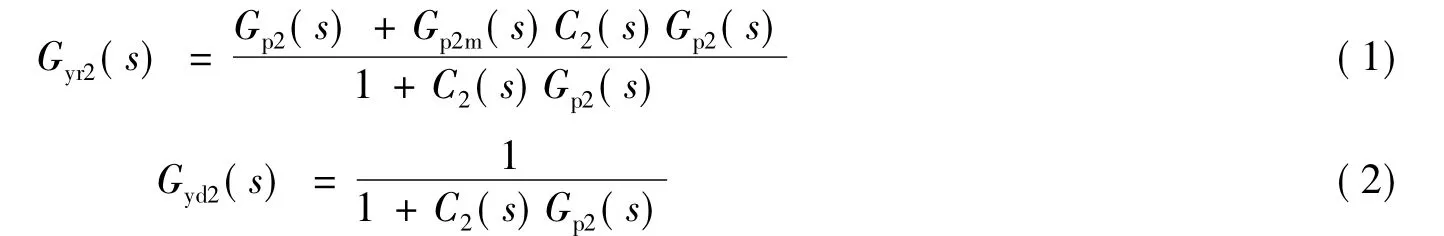
当模型精确时，即Gp2(s)=Gp2m(s)，则有:

主回路的设定值跟随特性和干扰抑制特性分别为:

由式(7)、式(8)可以看出系统的干扰抑制特性Gyd1(s)只与Q(s)有关，而与C1(s)无关;设定值跟随特性Gyr1(s)只与C1(s)有关，而与Q(s)无关。在这种情况下，Gyr1(s)与Gyd1(s)实现解耦。

设定值跟随特性Gyr1(s)和干扰抑制特性Gyd1(s)的解耦，使得设定值跟随控制器C1(s)和干扰抑制控制器Q(s)可以独立设计，以使系统同时获得良好的设定值跟随特性和干扰抑制特性，不需要在两种特性之间进行折中选择。而且，通过设计Q(s)，可以使并行串级控制系统具有良好的鲁棒性。

2 控制器设计

2.1 副控制器设计

由副回路的控制结构可知，副控制器C2(s)可依据内模控制方法设计，根据内模控制原理得[5-7]:

式中，Gm20为被控过程模型Gp2m(s)中的最小相位部分，f2(s)为低通滤波器，选择f2(s)的目的是保证C2(s)有理和使系统具有一定的鲁棒性。

考虑Gp2m(s)为一阶(一阶加时滞)的形式，因此f2(s)选用以下形式:

式中，λ2为滤波时间常数，则副控制器C2(s)为:

上式中只有一个待整定参数λ2，λ2的整定可参照文献[8]给出的最大灵敏度和参数之间的关系进行整定，一般λ2的取值范围为0.486τ2～4.146τ2.为了比较的公平性，λ2取值和对比文献中λ'2取相同的值。

2.2 主回路控制器设计

2.2.1 主回路设定值跟随控制器设计

从式(7)可以看出，系统设定值跟随特性表达式的分母中已不再包含时滞环节，针对主回路Gp1(s)，利用Dahlin控制算法的思想[9-11]，取设定值跟随期望特性如下:

式中，ε为时间常数。

将式(12)代入式(7)，对主回路GP1(s)可求得设定值控制器C1(s)为:

显然，式(13)为PI控制器形式，其中，KP1、TI1分别为比例增益、积分时间常数，其表达式如下:

式中，ε可以根据系统响应特性的要求来进行整定，减小ε可使系统的响应速度加快，增大ε可使系统的响应速度将变慢。

2.2.2 主回路干扰抑制控制器设计

为了使系统获得良好的抗干扰性和鲁棒性，主回路干扰抑制控制器Q(s)采用内模控制方法进行设计，即:

式中，Gm0为主过程Gp1(s)中的最小相位部分，f1(s)同样为低通滤波器。由于主过程Gp1(s)和主回路干扰通道模型GL1(s)相同且为一阶加时滞形式，因此设计f1(s)为:

式中，λ1是滤波器时间常数，ɑ为待定系数。

为了改进干扰抑制特性，根据式(8)确定α使(1-GmQ)的零点对消GL1(s)中的极点，即:

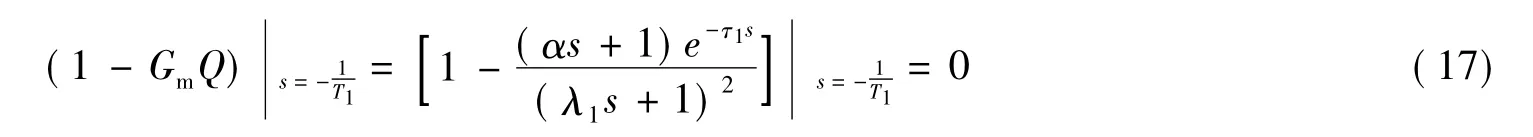
由式(17)可得:

则设计干扰抑制控制器为:

可知，当λ1减小时，系统的干扰抑制特性的响应速度变快，但鲁棒性变差;当λ1增大时，系统的鲁棒性增强，但干扰抑制特性的响应速度变慢。因此，干扰抑制控制器Q(s)的可调参数λ1的选取要权衡系统的鲁棒性和干扰抑制特性的响应速度。本文中，为了比较的公平性，λ1取值和对比文献中λ'1取相同的值。

3 仿真研究

为了验证本文方法的优越性，将本文方法与文献[4]的方法进行比较，选择超调量δ%和IAE作为系统性能的指标。IAE指标的定义如下:

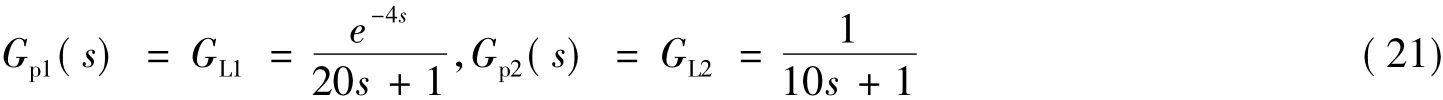
例1:选择文献[4]中的被控过程:

设控制系统的设定值输入为单位阶跃信号r1=1，在t=180时加入扰动d1=-0.5.在标称情况下得到系统的主、副回路输出响应曲线如图2、图4所示;当主回路控制对象Gp1(s)的时滞增大20%时主、副回路的输出响应曲线如图3、图5所示;控制系统的性能指标如表1所示。

图2 例1标称系统的主回路输出响应Fig.2 The primary loop output response of nominal system for example 1

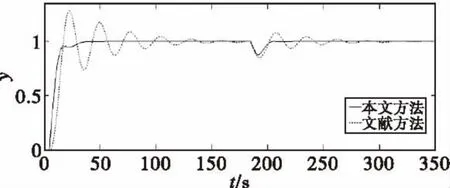
图3 例1摄动系统的主回路输出响应Fig.3 The primary loop output response of the perturbed system for example 1

图4 例1标称系统的副回路输出响应Fig.4 The deputy loop output response of nominal system for example 1

图5 例1摄动系统的副回路输出响应Fig.5 The deputy loop output response of the perturbed system for example 1

从图2-图5和表1中可以看出，在标称情况下本文主、副回路的设定值跟随性能和干扰抑制特性均优于文献[4]的方法;在模型Gp1(s)的时滞增大10%时本文主、副回路的设定值跟随性能和干扰抑制特性以及鲁棒性也同样优于文献[4]的方法。

4 结论

针对时滞过程的并联式串级控制系统，副回路采用了内反馈控制结构，有效的解决了副控制器对主回路的影响，以便于主控制器的设计。主回路采用了二自由度Smith预估控制，实现了设定值跟踪性和干扰抑制特性的解耦，使主、副回路的两种特性可分别有两个可调参数调整。仿真研究结果表明:该方法简便有效，可以使系统同时具有良好的动态响应性能和鲁棒性。

表1 超调量δ%和IAE性能指标Tab.1 Overshoot δ%and IAE performance index

[1]汪晓弘.并行串级控制系统及其性能分析[J].青海师范大学学报:自然科学版，2006(3):33-36.

[2]A SESHAGIRI RAO S，SEETHALADEVI S，UMA M.Chidambaram.Enhancing the performance of parallel cascade control using Smith predictor[J].ISA Transactions，2009，48:220-227.

[3]DOLA GOBINDA PADHAN，SOMANATH MAJHI.An improved parallel cascade control structure for processes with time delay[J].Journal of Process Control，2012，22:884-898.

[4]YONGHO LEE，MIKHAIL SKLIAR，MOONYONG LEE.Analytical method of PID controller design for parallel cascade control[J].Journal of Process Control，2006，16:809-818.

[5]曹新军，李华.基于鲁棒降阶模型的内模控制研究[J].电气传动自动化，2009，31(3):8-11.

[6]汤伟，施颂椒，王孟效.大时滞过程双自由度自整定内模控制[J].上海交通大学学报，2003，37(4):493-499.

[7]白继洲，张井岗.球杆系统的内模PID控制[J].太原科技大学，2013，34(3):166-170.

[8]赵志诚，刘志远，张井岗.一种积分时滞过程的内模PID鲁棒整定方法[J].华中科技大学学报:自然科学版，2011，39 (12):72-75.

[9]刘开培，饶玲娜.纯滞后系统的鲁棒性自调整Dahlin-Smith控制[J].仪器仪表学报，2002，23(3):376-377.

[10]DANIEL PETERSSON，JOHAN LÖFBERG.Model reduction using a frequency-limited H2-cost[J].Systems＆Control Letters，2014，67:32-39.

[11]SEBORG D E，EDGAR T F，埃德加，等.过程的动态特性与控制[M].北京:电子工业出版社，2006.

A New Parallel Cascade Two-Degree-of-Freedom Smith Predictor Control Structure for Processes with Time Delay

MA Wen-ting，ZHANG Jing-gang，ZHAO Zhi-cheng，QIN Na-na
(School of Electronics and Information Engineering，Taiyuan University of Science and Technology，Taiyuan 030024，China)

An improved parallel cascade control structure was proposed for the Delay Process.The deputy loop used the improved internal feedback control structure;it can effectively remove the influence of deputy controller for the main loop，thereby simplifying the design of the main controller.The main loop used the new type of 2-DOF smith predictor control structure，which can make the setpoint tracking performance and the anti-interference performance decoupling.Through the design of the controller that can effectively suppress the influence of process parameters change and disturbance on system performance，this new type of 2-DOF Smith predictor control method overcomes the disadvantages of conventional cascade control system and control algorithm is simple.It is also convenient to be used in actual system.Theoretical analysis and simulation results have shown the validity of the proposed control method.

parallel cascade control，internal feedback control structure，smith predictor control，two degree of freedom control

TP13

A

10.3969/j.issn.1673-2057.2015.04.007

1673-2057(2015)04-0273-05

2014-12-18

山西省自然科学基金项目(2011011011-2);山西省回国留学人员科研资助项目(2013-092);受校研究生科技创新项目支持

马文廷(1988-)，男，硕士研究生，主要研究方向为先进控制及应用的研究。