无圈竞赛图的内(外)生成树与路的计数
郭廷花,杨爱民
(1.山西金融职业学院基础部,太原 030008;2.山西大学数学科学院,太原 030006)
无圈竞赛图的内(外)生成树与路的计数
郭廷花1,杨爱民2
(1.山西金融职业学院基础部,太原 030008;2.山西大学数学科学院,太原 030006)
主要研究了无圈竞赛图中的外向生成树和指定点对的路问题,得到了图中全部外向生成树的计数公式τ+(Tn)=(n-1)!,在此基础上,得出图中全部内向生成树的计数公式τ-(Tn)=(n-1)!;两点之间全部路的计数公式σ(Tn)=2n-2,在此基础上,得出n阶无圈图全部路数为2j-i-1.
无圈竞赛图;外向生成树;路;计数
在本文的讨论中,无向图的概念和术语可参见[1],有向图的概念和术语可参见[2]。设G(V,E)为一无向简单图,其中V为顶点集为边集。若称其为 n阶空图,若,即G中每两点恰有一条边,称之为n阶完全图,记为Kn.对一个给定顶点数的图G,以上两种情况是含边数最少和最多的两种极端情况,亦即任意一个n阶图皆为Kn的子图。
在图的基本理论研究中,往往讨论一个n阶图中某种特定结构的子图的存在性问题,以及在存在的情况下的计数问题,进而如若图为赋权图,还要研究其优化问题。比如生成树问题,Hamilton圈问题,匹配问题等。对以上问题的研究,尤以生成树的结果最为完整。对于生成树的存在性,我们熟知有以下结果:
定理1 每个连通图都包含生成树。
对一个给定的简单图G,若用τ(G)记其全部的生成树棵数,则有以下的迭代公式:
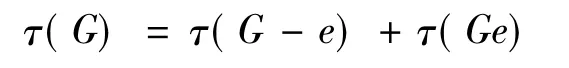
其中G-e是从G中删去边e得到的图,Ge是指对边e进行收缩。特别地,当G=Kn时,Clayey于1889年证明了如下公式[3]:

对于一般的图G,设D为其任一定向图,M为其关联矩阵,K为从 M中删去任意一行得到的矩阵,则:

这就是著名的矩阵—树定理[4]。
对于有向图D中的生成树(外向和内向)的存在性,文献中已有涉及,但其外向(或内向)生成树的个数,所见文献还未涉及。本文主要讨论一类特殊的有向图—无圈竞赛图中的外向(内向)生成树及D中指定两顶点之间全部路的计数问题。
1 预备知识
主要研究一类特殊的有向图—无圈竞赛图。一个有向图D由非空有限集V(D)和A(D)构成,V(D)和A(D)为有向图D的顶点集和弧集。一个有向图简记为D=(V,A).设(u,v)∈A(D)为D的一条弧,称顶点u为弧(u,v)的尾,v为弧(u,v)的头,并称顶点u支配顶点v,简记为uv,称D中顶点u,v是相邻的。如果D中存在弧uv或vu.

定义1 设D为有向图,D中的一条路是一个由顶点vi和弧ɑj交错排列而点不重的序列P= v1ɑ1v2ɑ2…vk-1ɑk-1vk,i=1,2,…,k-1,P中弧ɑi的尾是vi,头是vi+1.当v1=vk时,P称为圈,记为C.
路(圈)中所含的弧数称为路(圈)的长度。起点为x,终点为y的路称为x到y的路,简记为(x,y)路。
在无向图中,连通的无圈图称为树。设T为一棵树,对T的每一条边赋以方向后得到的图称之为定向树。在有向图的讨论中,我们更关心的是两类特殊的定向树—外向生成树和内向生成树。即设T是有向图D的一棵生成定向树,且T仅含一个入(出)度为零的顶点s,我们称之为外向(内向)生成树,并称s为T的根,用记号和分别表示有向图D中以顶点s为根的外向生成树和内向生成树。
任意给定一个有向图D,D中并不是总存在着外(内)向生成树。例如一条长度大于2的有向路,颠倒其任意一条弧得到的有向图,它既不存在外向生成树,亦不存在内向生成树,什么样的有向图D包含外向生成树或内向生成树呢?下面我们引入有向图强分解的概念,并利用此概念给出有向图D存在外(内)分支的一个充要条件。
D的一个强分支是一个最大的导出强连通有向子图。若D1,D2,…,Dt是D的全部强分支,显然有V(D)=V(D1)∪V(D2)∪…∪V(Dt),且V(Di)∩V(Dj)=φ(i≠j).我们把D1∪D2∪…∪Dt叫做D的强分解。有向图D的强分支有向图SC(D)是由收缩D的强分支并删去在这个过程中所产生的平行弧而得到的图,亦即如果D1,D2,…,Dt是D的强分支,则有 V(SC(D)) = {v1,v2,…,vt}和这意味着SC(D)中无有向圈存在,它的顶点可以排列为v1,v2,…,vt,使得当j>i时,vj到vi无弧,称为SC(D)的无圈序。对应SC(D)中零入度(零出度)的顶点的强分支称为D的初始(终止)强分支,其余的强分支称为中间强分支。
定理2 连通的有向图D包含一棵外向(内向)生成树当且仅当D有一个初始(终止)强分支。
定理3[5]每一个无圈有向图有一个出度为零的顶点和一个入度为零的顶点。特别的,每一个无圈有向竞赛图恰有一个出度为零的顶点和一个入度为零的顶点。
2 主要结果
设D为一个n阶无圈竞赛图。由于D不含圈,故每个顶点为一个强分支,它的强连通分支有向图即为本身。设其唯一的无圈序为v1,v2,…,vn,则显然下图为5阶无圈竞赛图及无圈序:

图1 5阶无圈竞赛图Fig.1 5-order acyclic tournament
定理4 设Tn为n阶无圈竞赛图,τ+(Tn)为其以v1为根的全部外向生成树,则τ+(Tn)=(n-1)!.
证明:设v1,v2,…,vn为其唯一的无圈序,v1为其唯一入度为零的顶点,由定理2知Tn存在外向生成树,由定理3知其根为v1.下面我们通过对n做归纳来证明上述定理。
当n=2时唯一的外向生成树即为本身Tn,当n= 3时,容易验证恰有两棵外向生成树。
设k=n-1时结论成立,即τ+(Tn-1)=(n-2)!.
讨论k=n时的情况。令D=Tn-vn,由以上假设.由于vn的入邻集,而Tn-1的任一外向生成树添加vn的任一外向弧均构成了Tn的一棵生成树,且这样得到的外向生成树是两两不同的,故τ+( Tn)=τ+( Tn-1) (n-1) = (n-1)!.
注:(n-1)!不是Tn的非同构生成树的棵树,而是Tn中不同的生成树的棵树;例T4中不同的生成树为6棵,而不同构的生成树仅有4棵。
把无圈竞赛图的每一条弧颠倒后所得之图与原图同构,仅是序号颠倒了,与上面证明完全相仿,因而得以下结论:
定理5 设Tn为n阶无圈竞赛图,τ-(Tn)为其以vn为根的全部内向生成树,则τ-(Tn)=(n-1)!.
定理6 设Tn为n阶无圈竞赛图,v1,v2,…,vn为其唯一无圈序,用σ(Tn)记其从v1到vn的全部不同的路的数目,则σ(Tn)=2n-2.
证明:对Tn的唯一无圈序v1,v2,…,vn,称v1为起点,vn为终点,其余为中间顶点。对任意的中间顶点vi1< vi2< … < vik,其中vi1,vi2,…,vik是{2,3,…,n-1}的一个k个元素的组合。由Tn的结构知v1vi1,vi2,…,vikvn是Tn中一条由v1到vn的长为k+1的路,故从v1到vn的长为k+1的路的条数为Ckn-2,于是从v1到vn的全部不同路数为:
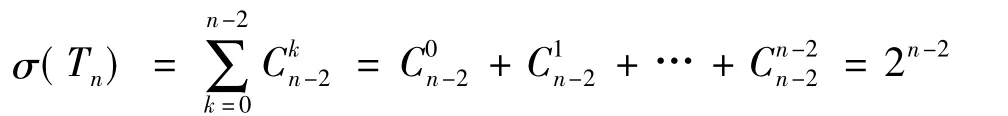
推论1 设Tn为n阶无圈图,v1,v2,…,vn为其唯一无圈序,则vi到vj(i<j)的全部路数为2j-i-1.
证明:由于Tn中由点vi,vi+1,…,vj的导出子图Tn<vi,vi+1,…,vj>为一j-i+1阶无圈竞赛图,据定理6立得。
注:定理6,推论1中的路数是指不同的路数,而非不同构的路数。例T4中从v1到v4不同的路数24-2=4条,而不同构的路数为3条。
[1]BONDY J.A,Murty USR.Graph Theory with Application[M].New York:Amercian Elserier,1979.
[2]BANG-JENSEN J,GUTIN G.Digraphs Theory:Algorithms and Applications[M].London:Springer Verlag,2001.
[3]CAYLEY A.A theorem on tree[J].Quart.J.Math,1889(23):276-378.
[4]KIRCHHOFF G.Uber die Auflosung der Gleichungen,auf welche man bei Untersuchung der linearen Verteilung Strome grfurht wird[J].Ann.Phys.chem,1847(72):497-508.
[5]LUO YONG-PING,YANG AI-MIN.A Lower Bound of the Number of Hamilton Path for Tournament[J].华北工学院学报,2004(6):438-440.
The Count of In-branching(out-branching)and Path on Acyclic Tournaments
GUO Ting-hua1,YANG Ai-ming2
(1.Basic Department,Shanxi Professional College of Finance,Taiyuan 030008,China; 2.School of Mathematical Sciences,Shanxi University,Taiyuan 030006,China)
Out-branchings and paths in the acyclic tournaments are discussed.Two count formulas of all out-branchings and all paths from initial vertex to terminal vertex in a acyclic tournament were got as τ+(Tn)=(n-1)!and σ(Tn)=2n-2,two count formulas of all in-branchings and all paths of order acyclic graph were got on the above basis as σ(Tn)=2n-2and 2j-i-1.
acyclic tournament,out-branching,path,count
0517.5
A
10.3969/j.issn.1673-2057.2015.04.018
1673-2057(2015)04-0323-03
2015-04-08
郭廷花(1979-),女,讲师,硕士研究生,主要研究方向为图论理论及算法的研究。

