基于Newmark－β法的换热管振动反问题的求解方法

徐 波，吴远峰，苏文献，许 伍

（上海理工大学 能源与动力工程学院，上海 200093）

换热器是化工、石油、动力、食品、航天以及其他工业部门的通用工艺设备，在国民经济和工业生产领域中起着至关重要的作用［1］.它的机械结构性能以及传热性能的好坏将直接影响产品质量、实际生产中能源的综合利用率，以及整个系统运行的经济性、安全性和可靠性.在各种形式的换热器中，管壳式换热器由于结构简单、用材范围广、清洗方便、适应性好、生产成本低、运行安全可靠、流量大、耐高压高温等特点在产量和应用范围等方面处于主导地位.在世界各国工程师的共同努力下，换热器的诸多领域虽然取得了可喜的进步，但仍有一些问题至今未能解决，特别是机理复杂的流体诱导振动问题，成了制约换热器进一步发展的关键因素.

目前诸多学者在预防换热器管束振动正问题方面做了大量的试验和研究，取得了很多进展，提出了不少理论见解和试验判据.很多方法都可以有效避免管束的共振，但是由于流动的复杂性以及振动因素的不确定性，仍然不能从根本上解决流体诱导换热器的管束振动.几十年来，许多学者对振动反问题产生了极大的兴趣，也提出了一些巧妙的反问题求解方法［2－4］，BUSBY等［5］提出了对受正弦和随机激励的间隙支撑单自由度系统冲击力的估算方法，在时域范围内成功识别出了激励的位置；WU等［6］使用时域分析技术研究了若干个同时作用的激励的分离识别问题，采用了所谓的反卷积谱分析法，该方法对处理非分散现象是非常有用的，但是不能用于处理离散的弯曲波［7］.

求解这些反问题的主要困难是问题本身的病态和求解过程的数值病态，这也就导致了反问题求解方法对测量信号的噪声扰动特别敏感.采用正则化技术——奇异值分解和优化技术，该病态问题能得到部分的解决.由于求解精度问题，本文将采用WHITON［8］和DOYLE［9］提出的一些通用方法，在时域内，采用Newmark－β法直接识别换热管所受的载荷，完成载荷的识别.

1 Newmark－β法

1959年，NEWMARK提出了一种计算振动动力响应方法的假设，该假设可以看成是线性加速度方法的推广.Newmark－β法一般用于求解正问题，即根据加载的力求解结构的位移、速度和加速度.由于其良好的收敛性，计算结果精度很高，适用性很广.Newmark－β法所采用的方程为：

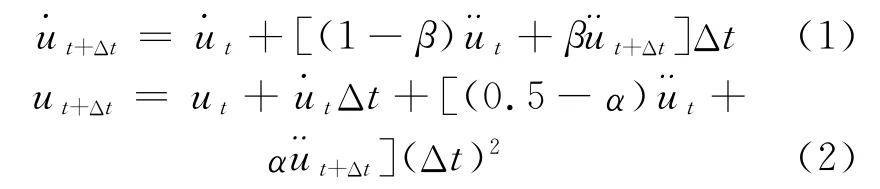
计算步骤可以简单归纳为两个步骤.

步骤一 初始计算

①计算结构的刚度矩阵K、质量矩阵M和阻尼矩阵C.

②根据初始条件u0和，计算.

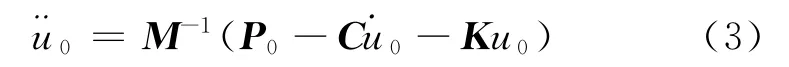
③选取合适的时间步长Δt和参数α和β，计算积分常数.

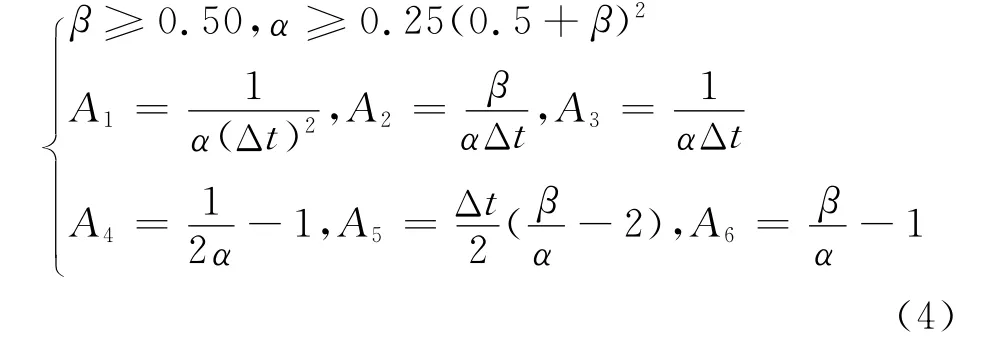
④计算有效刚度矩阵K′.

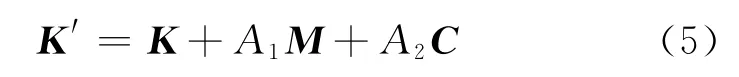
步骤二 对于每一时间步长

① 计算t＋Δt时刻的有效载荷向量P′.

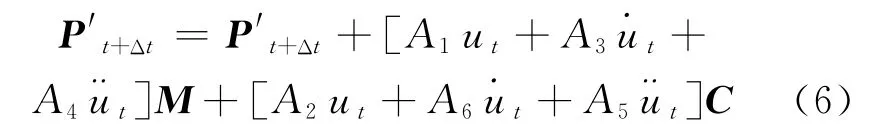
式中：Pt＋Δt为t＋Δt时刻的载荷向量.

②求解t＋Δt时刻的位移.

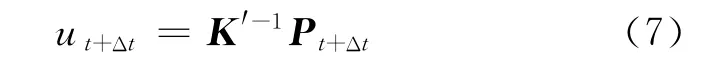
③计算t＋Δt时刻的加速度和速度.

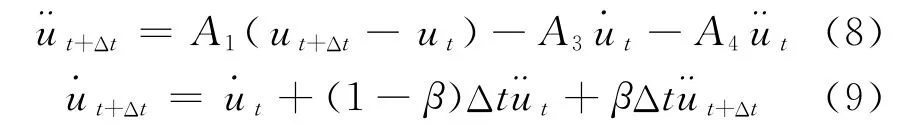
2 Newmark－β反分析法原理

Newmark－β法是在线性加速度的基础上发展起来的一种计算结构动响应的数值算法，该算法具有很好的数值稳定性和计算精度.由于广泛的适用性，在一定条件下可以保证算法的无条件稳定性，这些条件可以反向利用在逆问题上的求解.

基于时间推进法，可以知道与时刻t相关的量是已知的，求t＋Δt时刻的量，因此可以令t时刻的有效载荷向量对式（7）做如下变形：

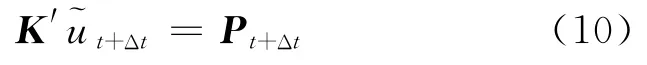
式中：为t＋Δt时刻的测点位移.

在每一个微小的时间步内，对于线弹性系统，根据叠加原理，可得

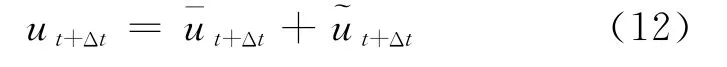
在t＋Δt时刻，由式（11）可知，P′t为t时刻的节点有效载荷向量，为已知量.求解方程式（11）可以得到t＋Δt时刻位移分量

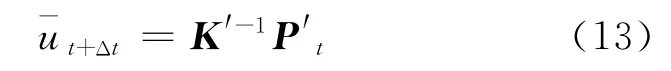
设在t＋Δt时刻，节点i上作用的单位节点载荷为，则有

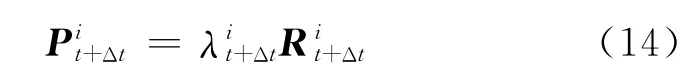
因此，求解第i节点上施加的载荷的问题就转化为求解载荷系数的问题.式（10）可以改写为

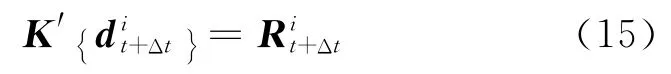
求解上式，可以分别得到单独在节点i处施加单位载荷时体系的位移向量，再根据式（14），则方程式（10）的解必定满足以下关系：

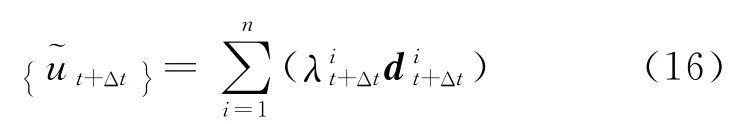
设有m个测点，在已知测出t＋Δt时刻的位移（或速度和加速度）值（k＝1，2，…，m），根据Newmark－β法，有

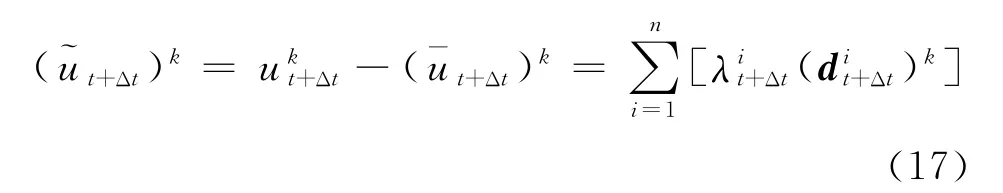
式（17）实际上是具有n个未知数（i＝1，2，…，n），m个测点位移（k＝1，2，…，m），可以形成m个方程组成的线性方程组

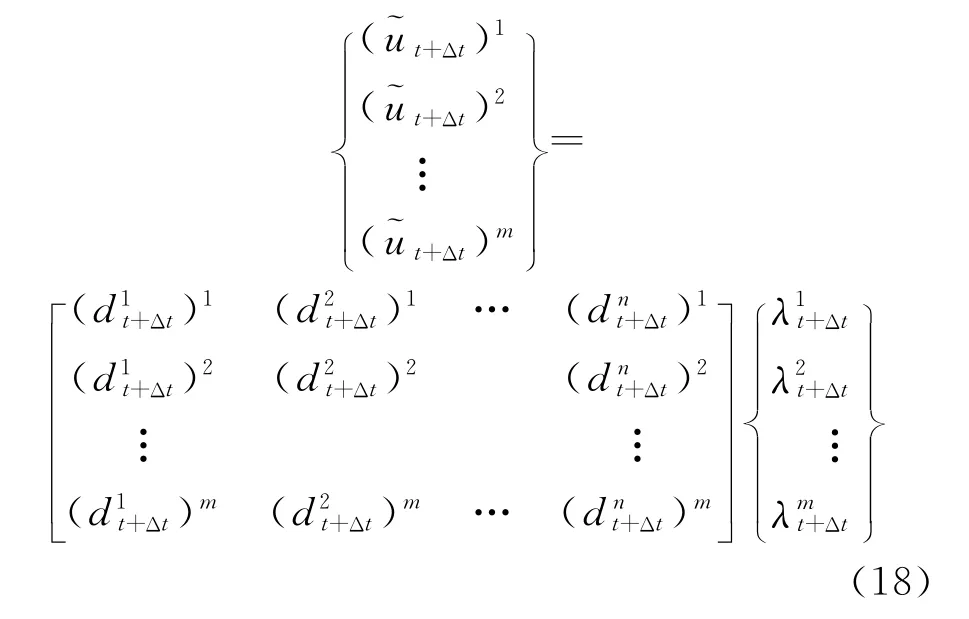
令

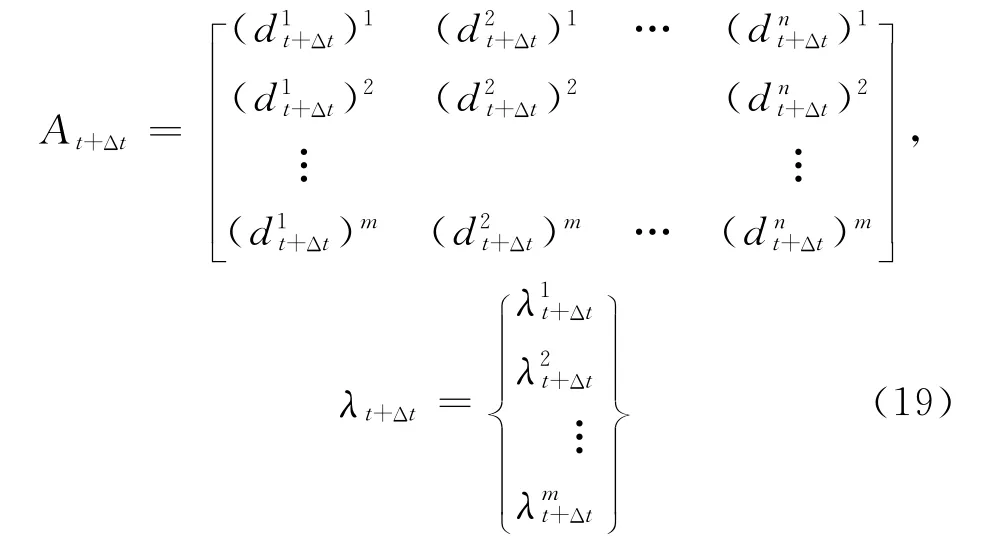
则，方程组可以改写成

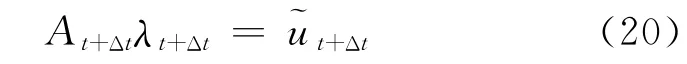
当m＝n时，解式（17）就可以求得（i＝1，2，…，n），代入式（14）可以得到，即t＋Δt时刻的振动载荷.若求出每一时刻的振动载荷，则可以得到振动载荷的时程.

当m＜n时，测点数小于要求解的未知数，故不能识别出振动载荷；当m＞n时，测点数大于要求解的未知数，可以采用最小二乘法得到高精度的结果，以消除误差.

2.1 算例分析

利用Newmark－β反分析法原理，在 MATLAB编程，验证理论推导过程的正确性.

已知：梁的长度L＝10 000mm，弹性模量E＝197GPa，截面面积S＝1 000mm3，截面惯性矩I＝108mm4，在梁的某位置处施加简谐载荷F＝1 000sin（t）.取：时间步长Δt＝0.1s，参数α＝1／4，β＝1／2，作用时间t＝10.0s，空间步长ΔL＝500 mm，采用基于Newmark－β法的 MATLAB程序，不考虑阻尼影响，可以得到各个节点的位移、速度和加速度时间历程曲线.由于加速度的精度更高，因此显示加速度时间历程曲线，如图1所示.

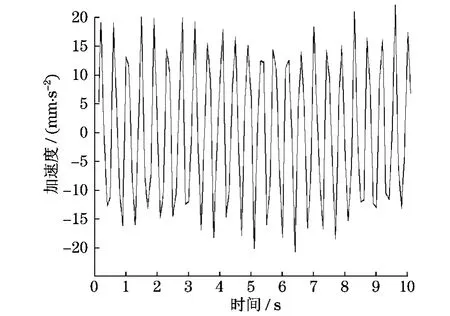
图1 各节点的加速度随时间的变化曲线Fig.1 Acceleration curve of each node with time

根据其中的任意一个加速度历程曲线，按照Newmark－β反分析法，可以得到载荷的识别曲线，如图2所示.

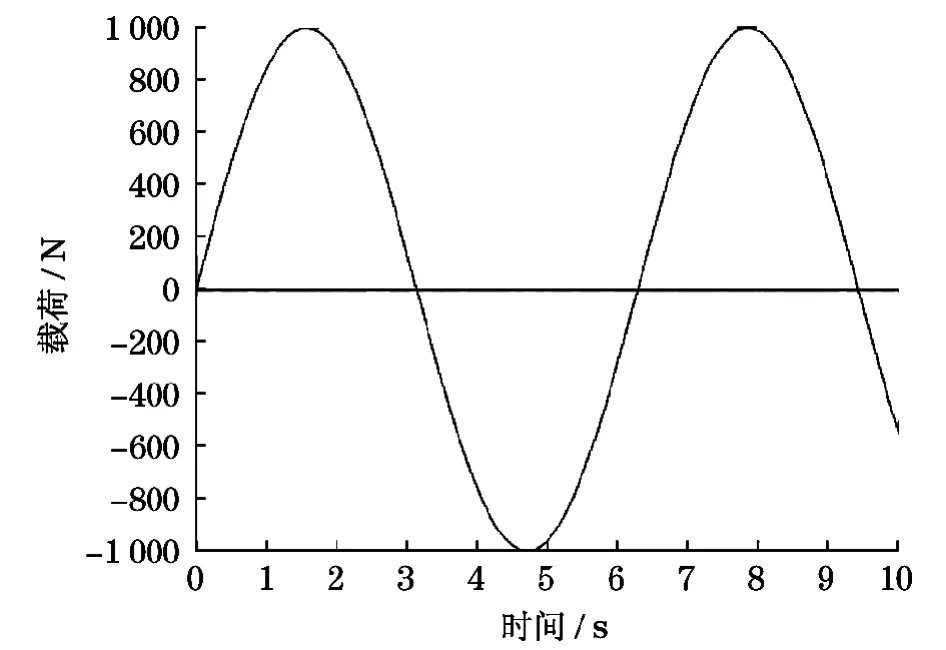
图2 加载点的识别载荷随时间的变化曲线Fig.2 Identification load curve of loading node ith time

从图2可以看出，在不考虑阻尼和环境噪声的影响下，识别载荷和加载载荷基本上是一致的.以上只对一个加载载荷进行了计算，同样地对于在多个节点上施加不同的载荷时程，也可以按照此方法完成振动载荷的识别.需要指出的是，在实际工程中，位移、速度和加速度的时间历程曲线是需要进行测量获得的，并作为已知条件进行使用，同时选择合的步长和参数，采用最小二乘法排除可能的误差，这样得到的识别载荷才有一定的精度和可信度.

3 结语

本文根据换热管在激励载荷作用下的响应，提出了应用Newmark逆分析法求解在已知该振动响应下系统所受的激励.在激励载荷识别时，提出了基于时域范围内的识别方法，初步探索了一种较为简单的管壳式换热器管束振动反演问题的计算方法，即激励载荷识别技术，为今后全面分析整体结构的振动正反问题做铺垫.

［1］郑津洋，董其伍，桑芝富.过程设备设计［M］.北京：化学工业出版社，2010.ZHENG Jingyang，DONG Qiwu，SANG Zhifu.Process equipment design［M］.Beijing：Chemical Industry Press，2010.

［2］PRESS W H，TEUKOLSKY A A，VETTERLING W T，et al.Numerical recipes：theartof scientific computing［M］.Cambridge：Cambridge University Press，1992.

［3］GROETCH C W.Inverse problems in the mathematical sciences［M］.Wiesbaden：Vieweg and Sohn，1993.

［4］HANSEN P C.Regularization tools［J］.Numer Algorithms，1994（6）：1－35.

［5］BUSBY H R，TRUJILLO D M.Solution of an inverse dynamics problem using an eigenvalue reduction technique［J］.Computers ＆ Structures，1987，25：109－117.

［6］WU E，YEH J C.Identification of impact forces at multiple locations on laminated plates［J］.Journal of American Institute of Aeronautics and Astronautics，1994，32：2433－2439.

［7］KIM J T，LYON R H.Cepstral analysis as a toll for robust processing，deverberation and detection of transients［J］.Mechanical Systems and Signal Process，1992（6）：1－15.

［8］JORDAN R W，WHISTON G S.Remote impact analysis by use of propagated acceleration signals：comparison between theory and experiments［J］.Journal of Sound and Vibration，1984，97：53－65.

［9］DOYLE J.Wave propagation in structures：an FFT－based spectral analysis methodology［M］.New York：Springer Verlag，1989.