分阶式双圆弧齿轮的动态建模与特性分析

宋雪萍，王际帆，刘元伟，李朝峰，闻邦椿

（1.大连交通大学 机械工程学院，辽宁，大连 116028；2.东北大学 机械工程与自动化学院，辽宁，沈阳 110819）

随着现代齿轮传动技术的发展，对齿轮的动态性能的要求越来越高，对齿轮传动的强度、振动和噪声的要求更加严格.渐开线齿轮轮齿抗弯强度高，但接触强度、耐疲劳强度等方面都不如圆弧齿轮.双圆弧齿轮是一种性能优良的动力传动齿轮，具有承载能力高、接触强度高、跑合性能好、加工方便、无根切现象等优点.由于圆弧齿轮容易形成油膜，齿面相对滑动小，耐疲劳强度高，所以特别适合于高速旋转［1－3］.在化工、石油等领域，以及高速传动如齿轮泵、汽轮机、鼓风机等设备上也广泛应用.齿轮泵是目前应用双圆弧齿轮的主要对象，圆弧齿轮是齿轮泵的最佳齿形，我们通过对泵瞬间排量的积分计算发现，圆弧齿轮泵的瞬间排量是一个定值，它不随转角发生变化，而渐开线齿形齿轮泵的瞬间排量与齿轮转角成平方关系，呈抛物线规律变化，所以渐开线齿轮泵做到大排量有点困难，会出现流量脉动大、噪声大、振动大等问题.将齿轮泵的齿形改造成双圆弧齿形之后，可降低流量脉动，降低噪音，实现高压.文献［4，5］对双圆弧采用传统的建模方法建立了齿轮齿形，并对齿轮进行了齿根应力的分析.本文以PTC公司的三维CAD／CAM参数化设计系统Pro／E软件为工具，结合双圆弧齿轮的结构特点，对分阶式双圆弧齿轮进行了精确的三维建模，并且运用有限元理论对双圆弧齿轮进行结构特性分析，为动力学分析研究打下基础.

1 双圆弧齿轮的模型的建立

分阶式双圆弧齿轮用圆弧连接凸、凹工作齿面，所以过渡面呈台阶形，这种齿形啮合时，非工作齿面之间形成一个较大的空隙，避免了非工作齿面发生接触的缺点.这是分阶式圆弧齿轮的一个优点.另一个优点是增大了凹齿齿根厚度，从而提高了弯曲强度［6］.由于圆弧齿轮圆柱齿形是法平面内工作齿廓为圆弧的基本齿条经过包络运动所形成的，因此为了保证传动的连续性，圆弧齿轮传动必须是斜齿圆柱齿轮.这是一种平行轴圆柱齿轮传动，具有轴向共轭、点接触的传动特点，其端面重合度为零.所以所给的齿廓基本上都是齿条在法平面内的齿廓［7］.

1.1 设置齿轮参数

由于双圆弧齿轮是一个空间螺旋体，若采用传统的建模技术很难实现齿轮的曲面造型，而由齿轮的端面形状沿螺旋线拉伸成空间螺旋面的方法进行建模是可行的，但是由于齿形是由四段圆弧组成，所以建模过程非常复杂.建模过程如下：

（1）首先设置齿轮的基本参数：齿数z、模数m、压力角α1、螺旋角β、齿宽b等.

（2）建立齿轮的基本尺寸的关系

分度圆直径d：d＝mz／cosβ

齿顶圆直径da：da＝d＋2ha.

齿根圆直径df：df＝d－2hf

式中：ha＝h＊am，hf＝h＊fm，h＊a＝1，h＊f＝1.25

（3）建立双圆弧齿轮的齿面方程式

圆弧上各点坐标值可由圆心位置（X，L）、圆弧半径ρ和齿形角α确定.建立圆弧齿轮齿面的普遍方程：

式中：β为螺旋角，右旋为正，左旋为负；r为节圆半径；φ为齿轮转角；x，y，z为齿轮齿廊上某点的坐标值；β′为基本齿廊所在截面与齿条端面的夹角.

令β′＝0，得端面圆弧齿轮齿面方程：

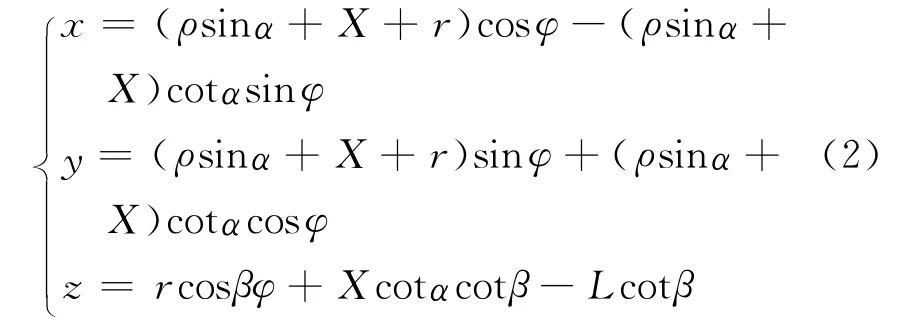
根据齿面方程（2）建立圆弧齿轮的主要接触表面圆弧模型.齿形由4段圆弧组成：凸齿工作圆弧、过渡圆弧、凹齿工作圆弧和齿根圆弧，如图1所示.

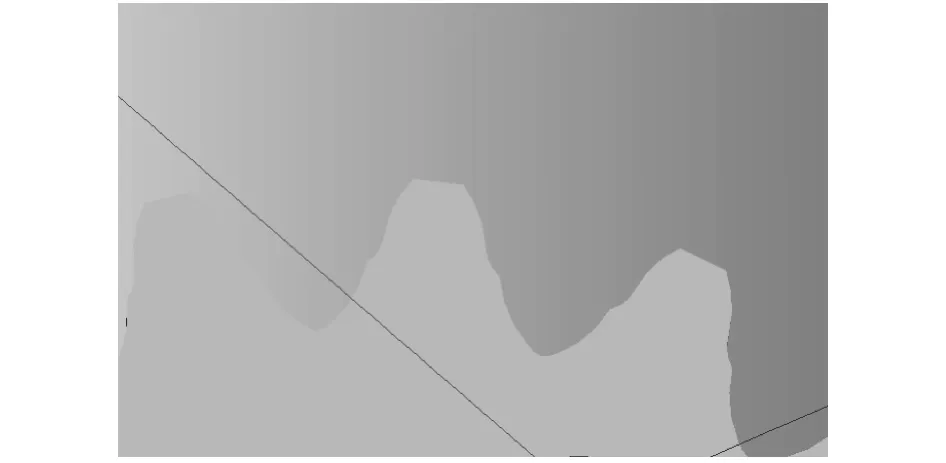
图1 齿形图Fig.1 Profile diagram

（4）建立螺旋线方程

双圆弧齿轮的轮齿在基圆柱表面呈螺旋分布，螺旋线方程为

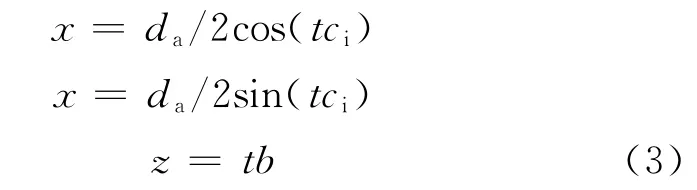
式中：ci＝2ci0180／πda，ci0＝btanβ；t为时间，0＜t＜1.

2 齿轮有限元模型的分析

对齿轮进行模态分析的目的就是要求出齿轮的各阶固有频率及其对应的振型，因此只需对模型的自由度进行约束.将约束施加在齿轮的内孔圆柱面上，设定模态提取阶数为15阶.频率依次为：0.0000，0.0000，0.0000，0.132 32×10－5，0.175 37×10－5，0.207 28 × 10－5，8.946 8，8.958 7，13.096，13.182，16.450，19.685，19.698，24.605，24.770Hz.结果分析如下：

因为篇幅有限，文中仅列出了其中部分的振型图.从图2中可以看出，前6阶是刚体运动.7，8阶为对折振，主要表现为轴向规则波浪振型，端面上为规则多边形振型，总体表现为结构扭曲型的对折振.9，10阶表现为轴向基本无振动，各端面上表现为相对扭转振动.11阶表现为收缩成伞状振型.12，13阶表现为齿轮沿径向伸缩，端面出现多边形振型，轴向基本无振动.14，15阶表现为圆周振动，轴向基本无振动，端面上为圆周方向的振动.

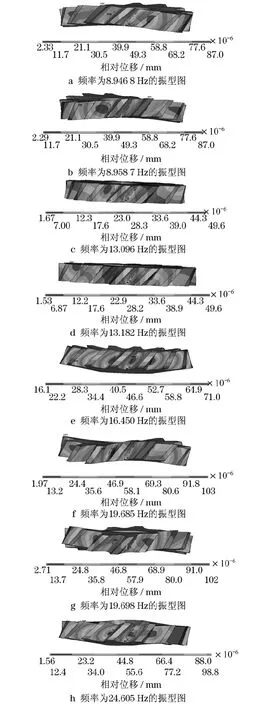
图2 部分频率振型图Fig.2 Partial frequency vibration diagram

3 齿轮啮合特性分析

由于双圆弧齿轮的齿廓是凹凸啮合，有较大的综合曲率半径，因此有很高的接触强度.由于是一种点啮合传动，所以必须在满负荷工作前经过跑合磨损，使理论上的点接触变形为局部的面接触.由于制造和装配误差以及齿面的不平度各处不一致等因素，在传动过程中齿面受到不均匀的载荷作用而引起接触齿面不均匀的磨损.在双圆弧齿轮的跑合过程中，随着齿面的逐渐磨损，凸齿圆弧半径逐渐增大，凹齿圆弧半径逐渐减小，两齿面逐渐贴合，形成较好的接触区.随着载荷的增加，轮齿的弹性变形增大，齿面接触区的形状也随着改变.如图3所示.

图3 双圆弧齿轮的接触跑合过程Fig.3 Process of double circular arc gear contact

圆弧齿轮啮合的重要条件是必须保证重合度大于1.重合度公式为

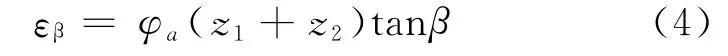
式中：εβ为重合度；z1，z2分别为大小齿轮的齿数，φa为齿宽系数.

根据式（4），得出εβ＝1.520 93，满足啮合条件.

双圆弧齿轮在运转中，总的接触齿数在不断变化，而接触点对数也在不断变化，因此双圆弧齿轮的载荷分配比渐开线齿轮复杂得多.多点啮合系数是确定双圆弧齿轮接触强度的重要依据，而多齿对啮合系数又是弯曲强度计算的重要依据，所以考察双圆弧齿轮的载荷分配必须首先考察它的多点啮合特性.

同一个齿上两个接触点间的轴向距离qTa为

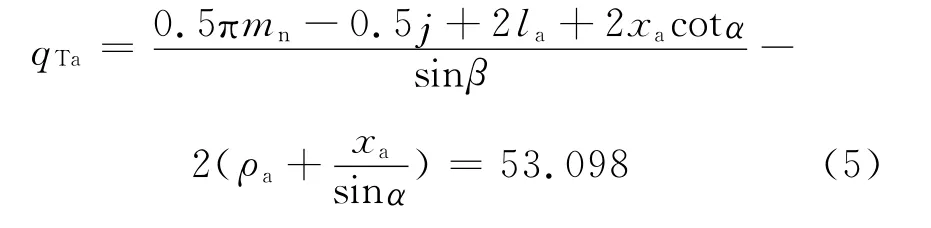
式中：mn为齿轮法向模数；la为凸齿齿轮廊x方向的圆心偏移量；xa为凸齿齿轮廊y方向的圆心偏移量；ρa为凸齿齿廊圆弧齿轮的传动侧隙.

剩余齿宽Δb为

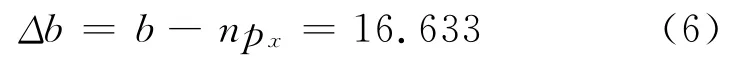
式中：px为轴向齿距.

因为px－qTa＜Δb＜qTa，由此计算出圆弧齿轮啮合过程中的接触点数系数和啮合齿对系数的百分比，如表1所示.

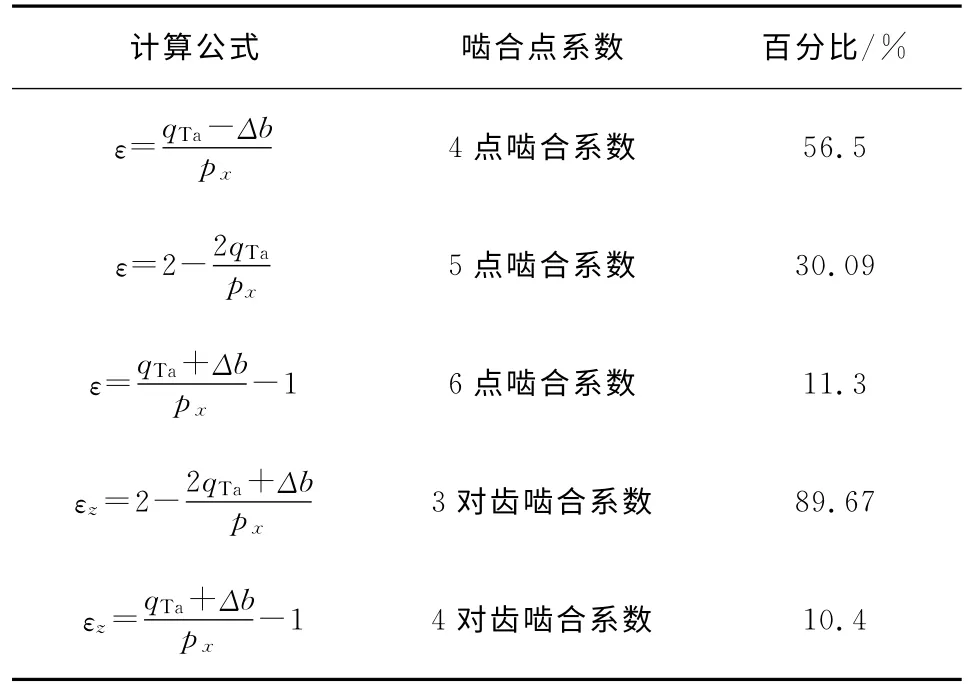
表1 齿轮啮合过程接触点数和啮合对数的百分比Tab.1 Gear meshing contact points and the meshing pairs percentage

由表1分析可知，整个齿轮副在一个转角的啮合范围内，有56.5%的时间为4点接触，30.09%的时间为5点接触，11.3%的时间为6点接触，89.67%的时间为3对齿啮合，10.4%的时间为4对齿啮合，与图3中的有限元分析过程基本一致.为了计算分析方便，取模型的一部分进行接触分析，如图4，5所示，分析其啮合过程的接触应力.

图4 啮合齿轮Fig.4 Meshing gear

从图5可以看出，两对齿啮合时的接触应力主要集中在凹齿的齿面上，为130.695MPa，比经验公式结果126.3MPa高了大约5MPa，结果非常接近.按照理论公式，这种齿宽参数的最大接触应力发生在4对齿啮合的范围内，但是由于啮合过程中接触轨迹间的载荷分配不均，造成了各个接触轨迹基本位于齿宽中部，只有两个接触点平均载荷最大，所以造成接触应力最大.

图5 齿轮啮合接触应力Fig.5 Contact stress of meshing gear

4 结语

通过上述研究可以得出如下结论：

（1）根据双圆弧齿轮的齿面方程导出端面的齿廓方程，结合双圆弧齿轮的特点，建立端面齿轮的齿形曲线，通过扫描混合建立了双圆弧齿轮的三维模型，这种方法为参数化建立非渐开线齿轮提供了理论基础.对齿轮进行了模态分析，从振型图上可以看出，齿轮除了存在轴向的波浪振型外，还存在端面的多边形振型和沿径向的伸缩振动，以及圆周振动.

（2）建立了双圆弧齿轮的接触模型，并且分析了齿轮在啮合过程中存在的3点接触、4点接触以及3对齿啮合和4对齿啮合的状态，得出了齿轮在外载荷的作用下的最大接触应力位置，并与理论值做了比较.研究表明，由于双圆弧齿轮在啮合过程中是点接触，并且是变化的，加上在啮合过程中载荷分配不均匀，造成某一时刻某一啮合点的接触应力最大.这种齿轮接触能真实模拟齿轮啮合情况，为齿轮的优化设计提供基础.

［1］屈文涛，沈允文，赵宁，等.双圆弧齿轮的静态和动态接触模型［J］.机械设计.2006，23（6）：27－29.QU Wentao，SHEN Yunwen，ZHAO Ning，et al.Static and dynamic contact model of double arced gear［J］.Journal of Machine Design，2006，23（6）：27－29.

［2］张秀亲，李瑞斌，张应顺.双圆弧齿轮齿根弯曲应力的研究［J］.机械科学与技术，2003，22（5）：764－766.ZHANG Xiuqin，LI Ruibin，ZHANG Yingshun.Research on the bending stress in tooth root of double circular－arc gear［J］.Mechanical Science and Technology，2003，22（5）：764－766.

［3］李强，何家宁，张伟.基于Pro／E和ANSYS的渐开线圆弧齿轮模态分析［J］.科学技术与工程，2011，11，（19）：4445－4448.LI Qiang，HE Jianing，ZHANG Wei.Involute－circular tooth gear model analysis based on Pro／E and ANSYS［J］.Science Technology and Engineering，2011，11（19）：4445－4448.

［4］黄利银，李金莲.双圆弧齿轮齿根曲率半径对齿根应力的影响［J］.机械设计与研究，2011，27（3）：56－59.HUANG Liyin，LI Jinlian.The Effect of the root stress by the root curvature radius of double－circular－arc gear［J］.Machine Design and Research，2011，27（3）：56－59.

［5］张拴玲，吴凤林，张东浩.准端面双圆弧齿轮的接触应力分析［J］.机械传动，2013，37（5）：79－81.ZHANG Shuanling，WU Fenglin，ZHANG Donghao.Analysis of contact stress for quasi－transverse double circular－arc gear［J］.Journal of Mechanical Transmission，2013，37（5）：79－81.

［6］邵家辉.圆弧齿轮［M］.北京：机械工业出版社，1994.SHAO Jiahui.Circular tooth gear［M］.Beijing：China Machine Press，1994.

［7］朱孝录.齿轮传动设计手册［M］.北京：化学工业出版社，2010.ZHU Xiaolu.Handbook of gear design［M］.Beijing：Chemical Industry Press，2010.