复式空心钢管混凝土柱抗爆性能及损伤研究

崔 莹，赵均海，张常光，孙珊珊，陈 兵

（1.西安石油大学机械工程学院，西安 710065；2.长安大学建筑工程学院，西安 710061；3.西北工业大学航空学院，西安 710072）

复式空心钢管混凝土柱抗爆性能及损伤研究

崔 莹1，3，赵均海2，张常光2，孙珊珊2，陈 兵1

（1.西安石油大学机械工程学院，西安 710065；2.长安大学建筑工程学院，西安 710061；3.西北工业大学航空学院，西安 710072）

通过爆炸试验，对复式空心钢管混凝土柱抗爆性能及损伤程度进行研究，并结合所得试验数据进行数值模拟，分析并建立柱的损伤评估准则。结果表明：在折合距离为0.14 m／kg1／3试验条件的爆炸荷载作用下，复式空心钢管混凝土柱迎爆面柱中发生了明显的塑性弯曲变形；柱迎爆面压力峰值柱中最高、柱底次之、柱顶最小，且爆炸冲击波对迎爆面柱中造成的破坏最为强烈、柱底次之、柱顶最小；柱端部节点强度与构件整体强度协调对提升复式空心钢管混凝土柱的抗爆性能尤为重要。最终建立了基于固端约束下复式空心钢管混凝土柱中挠度的超压－冲量（P－I）损伤准则及判定公式。

爆炸力学；复式空心钢管混凝土柱；爆炸试验；数值模拟；超压－冲量（P－I）曲线

由于全球范围内的爆炸事故和恐怖袭击频繁发生，常规建筑结构受到爆炸冲击作用的可能性不断增加。要使结构在爆炸冲击荷载作用下避免破坏，柱本身的抗爆性能起着非常重要的作用。复式空心钢管混凝土柱具有承载力高、塑性好、抗弯刚度大的特点，被广泛用做工程结构中的重要受力构件［1－4］。研究复式空心钢管混凝土柱的爆炸冲击破坏效应，进而建立其损伤评估方法具有重要的理论意义和工程应用价值。近年来，国内外学者对于爆炸冲击荷载作用下柱的动力响应开展了部分研究工作，主要采用数值模拟和试验分析的方法研究了流固相互作用下的有缺陷简支柱的动态弯曲特性［5－6］；柱端约束条件对框架柱在爆炸冲击波作用下的影响及框架柱抗爆分析简化计算［7］；钢筋混凝土柱和实心钢管混凝土柱在爆炸冲击荷载下的动力响应、抗爆性能、破坏形式及影响要素等［8－13］。但是对于本文所提及的复式空心钢管混凝土柱在爆炸荷载作用下动态响应的研究工作相对较少。本文以所开展的复式空心钢管混凝土柱爆炸试验结果为依据，对爆炸荷载下复式空心钢管混凝土柱的动态响应进行数值模拟，建立了固端约束下基于构件最大挠度的复式空心钢管混凝土柱损伤评估准则。

1 复式空心钢管混凝土柱爆炸试验

1.1 试件设计

复式空心钢管混凝土柱试件以文献［14］中所应用的钢管混凝土柱为原型进行设计。按照缩放比例1∶2及《无缝钢管尺寸、外形、重量及允许偏差》（GB／T17395－2008）中钢管规格的要求，外钢管采用国标外径为273 mm，壁厚为7 mm的无缝钢管，芯钢管选择为外径50 mm，壁厚为3 mm的普通直缝焊管。内填混凝土选择为C40的细石混凝土。柱脚参照《钢管混凝土结构设计与施工规程》（CECS28－2012）以及《多、高层民用建筑钢结构节点构造详图》（GJBT－543－01SG519）中端承式柱脚的构造进行设计，肋板与外钢管采用焊接连接，焊脚尺寸不小于10 mm。具体试件参数见表1所示。

1.2 试验准备

试件柱脚底板通过10.9级的M30高强螺栓与反力架完成固结。

试验所用的TNT药量为50 kg，爆心距为0.5m，爆心保持与柱迎爆面柱中等高，折合距离为0.14 m／kg1／3。现场示意图如图1所示。

表1 复式空心钢管混凝土柱试件设计参数表Tab.1 Design parameters of dup lex hollow CFST column

图1 试验现场示意图Fig.1 Schematic view of test site

1.3 试验结果分析

爆炸荷载作用下反力架整体完好，未发生断裂破坏，柱宏观变形如图2所示。

由图2（a）可以看出，在折合距离为0.14 m／kg1／3的爆炸荷载作用下，复式空心钢管混凝土柱迎爆面柱中发生了明显的塑性弯曲变形，经量测柱中挠度为195 mm。同时柱脚底板迎爆面右下角有轻微翘曲变形，这是因为右下角与地面固结的螺栓较其余螺栓连接紧密，螺栓提供的约束较好，导致柱向后移动趋势受阻，因而发生底板翘曲现象。

需要引起重视的是柱迎爆面柱底肋板上缘柱表面有一条细微未贯通裂缝存在，如图2（b）所示。分析出现此条细微裂缝的原因是由于柱中发生弯曲凹陷，而柱底节点因为有肋板的设计而强度高于构件，柱底迎爆面受到爆炸冲击波的剪切及拉伸作用所致。因此要使复式空心钢管混凝土柱的抗爆性能得到提升，柱端部节点强度如何与构件整体强度协调尤为重要。

图2 复式空心钢管混凝土柱宏观变形Fig.2 Macroscopic deformation of duplex hollow CFST column

2 复式空心钢管混凝土柱数值模拟

2.1 材料本构模型

数值模拟对象包括钢管混凝土柱、空气及炸药，均采用SOLID164单元模拟。单位制取为mm－ms－MPa。

（1）混凝土本构模型

选用LS-DYNA材料库中的111号*MAT＿JOHNSON＿HOLMGUIST＿CONCRETE材料模型［15］（简称HJ－C模型）来模拟混凝土材料在高应变率下的动力特性。

（2）钢材本构模型

选用LS-DYNA材料库中的3号*MAT＿PLASTIC＿KINEMATIC材料模型［16］来模拟钢管在高应变率下的动力特性。

（3）炸药和空气本构模型

采用LS-DYNA提供的*MAT＿HIGH＿EXPLOSIVE＿BURN高能炸药燃烧模型来模拟TNT炸药的爆轰。选择LS-DYNA提供的*MAT＿NULL材料模型对空气进行模拟。

2.2 材料状态方程

在LS-DYNA中，对炸药和空气等流体材料的处理，需要同时使用材料的本构模型和状态方程两种方式来描述材料的特性：采用本构模型来描述应力和应变的关系，即Δσij和Δεij的关系，采用状态方程来描述炸药和空气在爆炸发生后体积变形率与压力的关系，即ΔV／V和ΔP的关系。

（1）炸药的状态方程

采用*EOS＿JWL状态方程可以对爆炸过程中产生的压力做出与试验结果较为相近的预测。*EOS＿JWL状态方程的表达式为：

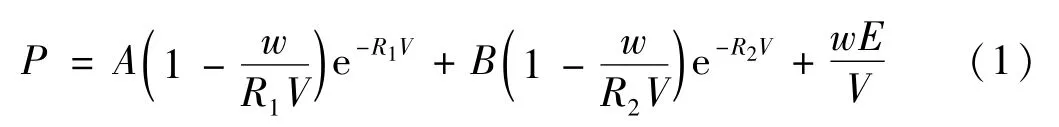
式中，P为爆轰产物的压力；V为爆轰产物的相对体积；E为爆轰产物单位体积初始内能；w、A、B、R1、R2为材料常数。

（2）空气的状态方程

采用线性多项式*EOS＿LINEAR＿POLYNOMIAL状态方程来模拟空气［16－18］。线性多项式*EOS＿LINEAR＿POLYNOMIAL状态方程为：

2.3 有限元模型

（1）几何模型及边界条件

为了真实模拟柱受爆炸冲击荷载后的动态响应，边界条件确定如下：钢管混凝土柱上下端为固端约束。空气区域按照文献［17］的建议及试验的具体要求确定如下：柱背爆面及两个侧面空气边界按照各超过柱边缘300 mm确定，上部边界按照柱顶预留200 mm确定，下部边界按照与地面相接处予以确定。同时模型在底部加设刚性反射面以模拟真实试验时冲击波在地面的反射，空气边界设定为透射边界［18］。建立的整体模型几何关系示意图如图3所示。

（2）有限元模型

空气和炸药考虑结点共用以及网格划分的尺寸效应［19－20］，单元大小确定为20 mm。共划分相应的SOLID164单元为534 050，计算时间设定为20 ms。所建立的有限元数值模型如图4所示。

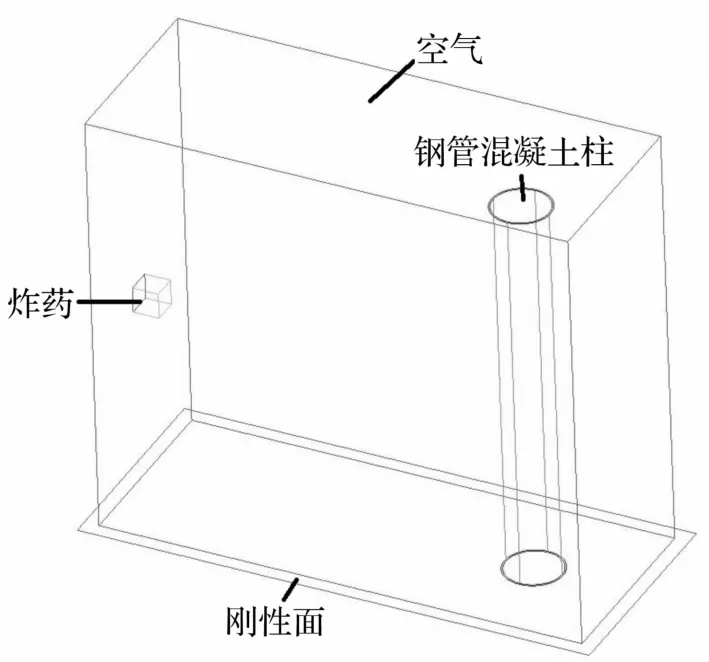
图3 几何模型示意图Fig.3 Sketch of geometric model

图4 复式空心钢管混凝土柱有限元模型Fig.4 Numericalmodel of duplex hollow CFST column

2.4 数值模拟结果

复式空心钢管混凝土柱的数值模拟结果如图5所示。

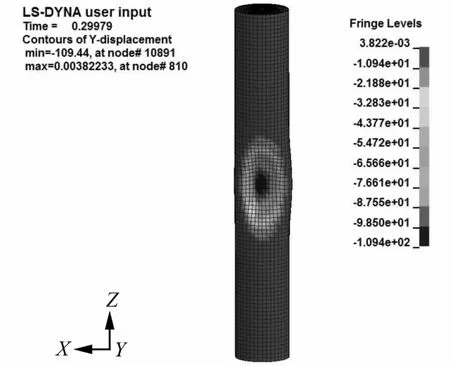
图5 复式空心钢管混凝土柱数值模拟结果（折合距离＝0.14 m／kg1／3）Fig.5 Result of numerical simulation model for duplex hollow CFST column （Scale distance＝0.14 m／kg1／3）

以试验所测得柱中的弯曲挠度来衡量数值模拟结果的准确性。经比较可以发现，数值模拟迎爆面柱中弯曲挠度为109.44mm，现场试验结果为195 mm，两者在同一数量级内，现场试验结果大于数值模拟结果，两者误差为43.9%。分析两者误差产生是由于数值模拟中柱的约束条件以及地面反射条件与现场试验均有较大差异，且空气域模拟有限。同时数值模拟是理想状态，而现场试验的条件复杂，加之爆炸试验采样率有限。文献［21］研究表明：当折合距离在0.1 m／kg1／3时，两者的误差会达到90%左右，且数值模拟结果均会小于实际爆炸试验结果。因此综合考虑上述各个方面因素，可以认为针对爆炸试验的数值模拟结果是合理的。

为了掌握柱在爆炸荷载下的动态响应情况，从数值模拟结果中提取柱迎爆面柱底、四分之一柱高、柱中、四分之三柱高和柱顶五个位置的柱位移时程曲线如图6所示。图中位移负值表明柱发生变形的方向与爆炸冲击波传播方向一致。

从图6中可以看出，柱迎爆面五个位置的变形均在6 ms左右达到稳定。其中，柱迎爆面变形由于约束和爆心位置两者的共同影响呈现柱中变形最大，两端变形最小的特征。从曲线的斜率来看，迎爆面五个位置变形均在2～4 ms的时间段范围内急剧增加，而后增加减缓趋于稳定。图6（a）中迎爆面柱底位移时程曲线在0.5ms左右的突变分析是由于刚性地面反射所致。将五个位置的最终塑性变形提取出来如表2所示。从表2中的数据可以看出，柱迎爆面的塑性变形量关于爆心近似成上下对称，同时柱底和柱顶均有少量的位移量，这与实际试验中实际构件的变形情况是一致的。

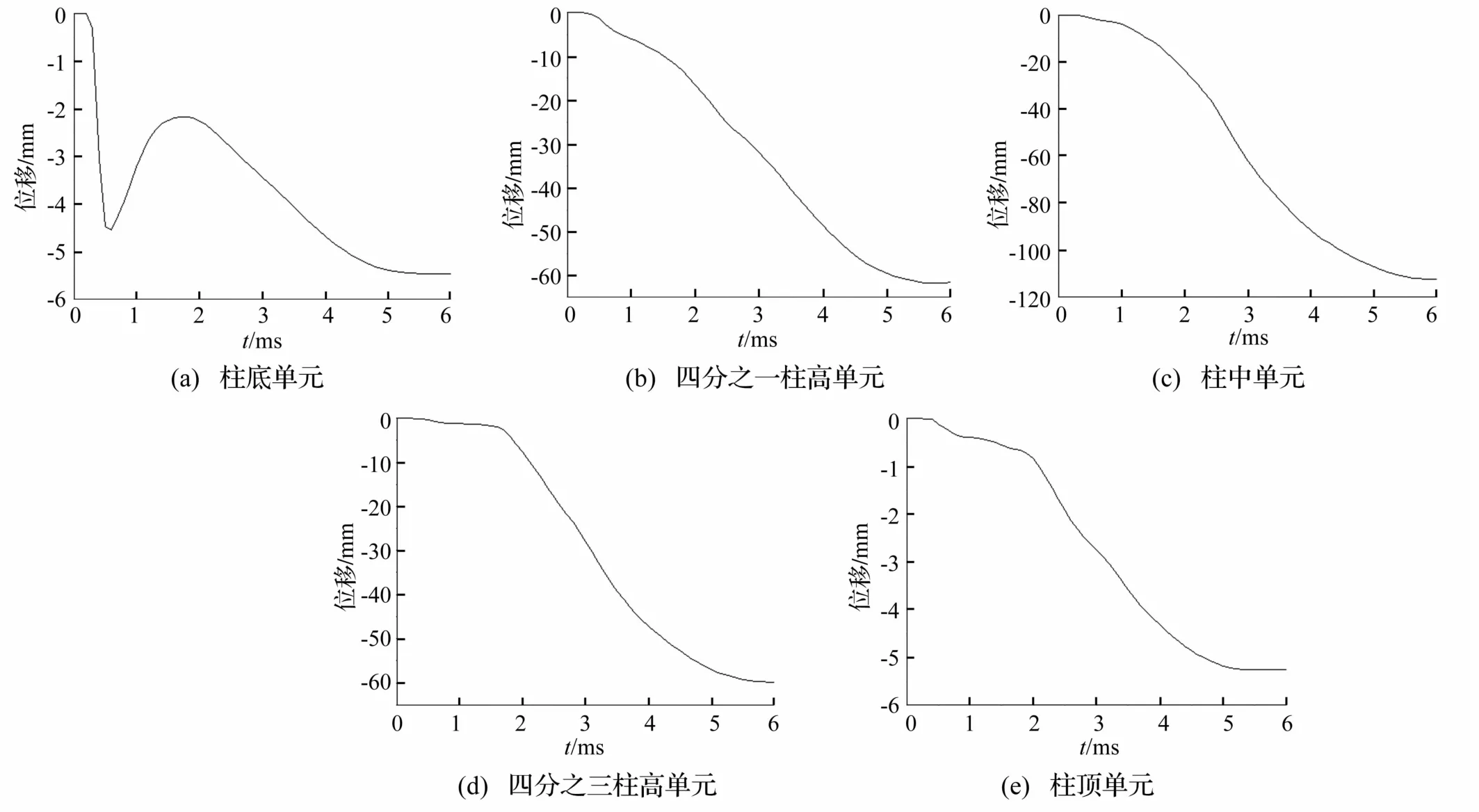
图6 柱迎爆面不同位置单元位移时程曲线Fig.6 Displacement-time curve of different position element on the column surface facing the explosive

表2 柱迎爆面不同位置最终变形量表Tab.2 Displacement value of different position element on the column surface facing the exp losive

在数值模拟结果中提取复式空心钢管混凝土柱迎爆面柱底、柱中和柱顶三个位置单元的压力时程曲线如图7所示。

从图7中可以看出，在50 kg药量，爆心距为0.5 m，折合距离为0.14 m／kg1／3的条件下，柱迎爆面柱底、柱中和柱顶的压力峰值分别为18.72 MPa，176.05 MPa 和4.17 MPa。柱中的压力峰值分别为柱底和柱顶的9.4倍和42.2倍。通过比对时间数据可以发现迎爆面上、中、下三个位置压力峰值产生的时间分别为0.3 ms，0.2 ms和0.3 ms，这说明爆炸冲击波到达迎爆面柱底、柱中和柱顶的时间几乎是同时的，而柱底的压力峰值大于柱顶的原因是因为在模型中添加了刚性面以模拟地面反射的缘故。

在迎爆面正压持续时间方面，柱顶、柱中和柱底三个位置的正压持时分别为2.5ms、2.2ms及1.3ms。因此综合考虑上述三个位置的压力峰值可以得出结论：爆炸冲击波对迎爆面柱中造成的破坏最为强烈、柱底次之、柱顶最小。

图7 柱迎爆面不同位置单元压力时程曲线Fig.7 Pressure-time curve of different position element on the column surface facing the explosive

3 复式空心钢管混凝土柱的损伤评估

3.1 损伤评估准则

目前针对柱构件损伤评估准则可以分为柱中最大位移、最大应力、最大应变以及柱竖向剩余承载力等［10］。确定损伤评估准则的主要原则是：与准则相关的复式空心钢管混凝土柱的整体特性应较容易通过试验或数值模拟方法得到，同时又便于针对实际工程开展。因此依据《石油化工控制室抗爆设计规范》（GB50779－2012）中5.6.3规定：在爆炸荷载作用下，柱构件支座处弹塑性转角允许值为2°。结合上述柱构件损伤评估准则要求，可以将控制柱构件支座转角等效为控制柱中塑性变形量，即柱中挠度不能超过柱计算高度的1／60。本文建立基于固端约束下复式空心钢管混凝土柱中挠度的超压－冲量损伤评估准则。复式空心钢管混凝土柱损伤评估准则可以简单表述为：柱中挠度小于柱计算高度的1／60，判定柱为安全；柱中挠度大于等于柱计算高度的1／60，判定柱为危险。柱中挠度示意图如图8所示。

3.2 复式空心钢管混凝土柱P－I曲线建立

以建立的爆炸荷载下复式空心钢管混凝土柱有限元模型为研究对象进行多次有限元数值模型的调整。每一次数值模拟后，均选择柱迎爆面几何中心的柱中单元，得到该单元的位移时程曲线。定义柱中挠度为f，柱计算高度为L，将进行了大量数值模拟试算后所得的压力和冲量数据点绘制在P－I平面内，从数据点中找出符合模型柱中挠度f＝L／60损伤等级分界点的超压冲量组合临界值，得到本文中复式空心钢管混凝土柱损伤等级分界线，即P－I曲线，如图9所示。

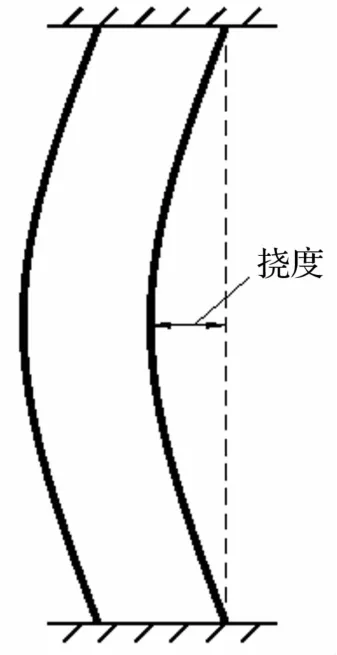
图8 柱中挠度示意图Fig.8 Schematic view of column deflection

图9中的P－I曲线的含义是：曲线将P－I空间划分为两个部分，若P、I组合的数据点落在该曲线的左下方，则表明复式空心钢管混凝土柱迎爆面柱中挠度没有超过L／60，变形仍在安全范围内，可以判定该柱为安全；若P、I组合的数据点落在该曲线的右上方，则表明复式空心钢管混凝土柱迎爆面柱中挠度超过L／60，变形在危险范围内，可以判定该柱为危险；若P、I组合的数据点落在该曲线上，则表明处于临界状态，基于安全考虑应判定该柱为危险。例如依据本文爆炸试验，进行数值模拟得到的柱中P＝176.05 MPa、I＝22.70 MPa·ms，该数据点落在P－I曲线的右上方，则可以判定该复式空心钢管混凝土柱危险。

3.3 P－I曲线拟合公式

为了使经过大量数值模拟后获得的复式空心钢管混凝土柱P－I曲线具有明确的数学含义，对图9中的P－I曲线进行数学表达式拟合。通过对图9中的数据进行分析可以发现，I和P近似成自然对数关系，因此经过反复尝试确定出P－I曲线可以用式（3）进行拟合表达。

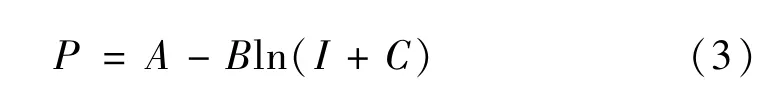
式中，P为爆炸冲击波峰值超压，I为爆炸冲击波正向阶段冲量，A、B、C为三个实常数，与复式空心钢管混凝土柱的损伤情况有关。

公式（3）拟合效果如图10所示。

由图10可以看出，采用本文推导拟合出的P－I曲线公式所绘曲线与数值模拟曲线基本吻合良好，因此，可以将公式（3）推广到一般情况，建立以迎爆面柱中挠度为指标的复式空心钢管混凝土柱损伤评估准则。例如以迎爆面柱中挠度为L／60＝30 mm作为判定指标，则公式（3）可以变换为式（4）：

此时A＝180.5；B＝92.08；C＝－0.5。

图9 复式空心钢管混凝土柱P－I曲线Fig.9 P－I curve of duplex hollow CFST column

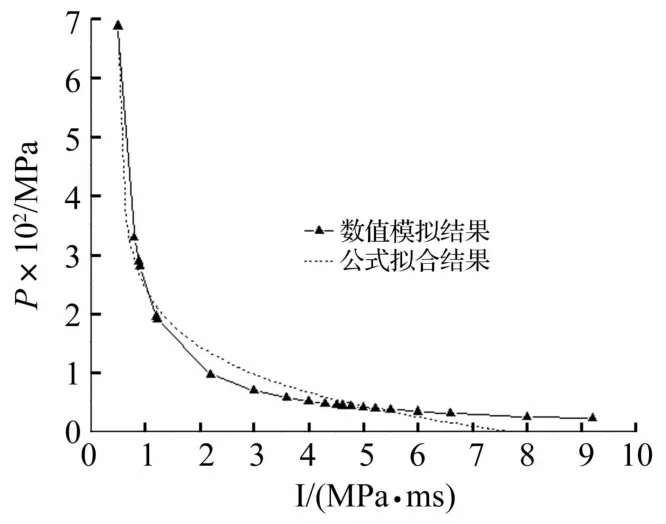
图10 公式拟合P－I曲线与数值模拟P－I曲线对比Fig.10 Comparison between fitting P－I curve by formula and P－I curve by numerical simulation

公式（4）适用于本文设计参数的、固端约束条件下复式空心钢管混凝土柱在爆炸荷载下的损伤评估。其他不同约束条件和设计参数的复式空心钢管混凝土柱可以依据文中所归纳的方法予以相应推导。

4 结 论

本文采用爆炸试验和数值模拟的方法研究爆炸荷载下复式空心钢管混凝土柱的抗爆性能及其损伤评估，主要结论如下：

（1）加强柱端部节点强度与构件整体强度协调可以提升复式空心钢管混凝土柱的抗爆性能。

（2）当爆心与柱中等高时，爆炸冲击波对迎爆面柱中造成的破坏最为强烈、柱底次之、柱顶最小。

（3）依据建立的复式空心钢管混凝土柱超压—冲量（P－I）损伤评估准则可以进行爆炸荷载下不同计算高度的、基于迎爆面柱中挠度固端约束复式空心钢管混凝土柱损伤评估。评价爆炸荷载下复式空心钢管混凝土柱的安全性能。

［1］蔡绍怀.现代钢管混凝土结构［M］.北京：人民交通出版社，2003.

［2］钟善桐.钢管混凝土结构［M］.3版.北京：清华大学出版社，2003.

［3］王志浩，成戎.复合方钢管混凝土短柱的轴压承载力［J］.清华大学学报：自然科学版，2005，45（12）：1596－1599.WANG Zhi-hao，CHENG Rong.Axial bearing capacity of composite-sectioned square concrete-filled steel tubes［J］.Journal ofTsinghua University：Science and Technology，2005，45（12）：1596－1599.

［4］黄宏，陶忠，韩林海.圆中空夹层钢管混凝土柱轴压工作机理研究［J］.工业建筑，2006，36（11）：11－14.

HUANG Hong，TAO Zhong，HAN Lin-hai.Mechanism of concrete-filled double-skin steel tubular columns subjected to axial compression［J］.Industrial Construction，2006，36 （11）：11－14.

［5］Hao H，Cheong H K，Cui S J.Numerical study of dynamic buckling of steel columns subjected to underground explosion ［J］.Engineering Materials，2002，233（1）：211－216.

［6］Cui SJ，Cheong H K，Hao H.Elastic-plastic dynamic response and buckling of steel columns under strong vertical ground motion［J］.Engineering Materials，236（1）：217－222.

［7］李国强，孙建运，王开强.爆炸冲击荷载作用下框架柱简化分析模型研究［J］.振动与冲击，2007，26（1）：8－11.LIGuo-qiang，SUN Jian-yun，WANG Kai-qiang.Research on a simplified frame column model to resist blast load［J］.Journal of Vibration and Shock，2007，26（1）：8－11.

［8］马云玲，谢冰，何大治，等.圆钢管混凝土爆炸响应的数值分析［J］.武汉理工大学学报，2010，32（14）：120－124.

MA Yun-ling，XIE Bing，HE Da-zhi，et al.Numerical analysis on blasting response of circular concrete-filled steel tubes［J］.Journal of Wuhan University of Technology，2010，32（14）：120－124.

［9］吴赛.爆炸荷载下复式钢管混凝土柱动力响应研究［D］.西安：长安大学，2012.

［10］师燕超.爆炸荷载作用下钢筋混凝土结构的动态响应行为与损伤破坏机理［D］.天津：天津大学，2009.

［11］孙建运.爆炸冲击荷载作用下钢骨混凝土柱性能研究［D］.上海：同济大学，2006.

［12］Fujikura S，Bruneau M.Experimental investigation of seismically resistant bridge piers under blast loading［J］.Journal of Bridge Engineering，2011，16（1）：63－71.

［13］Fujikura S，Bruneau M，Diego lopez-garcia.Experimental investigation of multihazard resistant bridge piers having concrete-filled steel tube under blast loading［J］.Journal of Bridge Engineering，2008，13（6）：586－594.

［14］程宝坪.深圳赛格广场钢管混凝土柱－钢结构施工特点［J］.施工技术，2000，29（6）：2－5.

CHENG Bao-ping.Constructional features of steel-pipe concrete column and steel structure of shenzhen saiger plaza ［J］.Construction Technology，2000，29（6）：2－5.

［15］Randers Pehrson G，Bannister K A.Airblast loading model for DYNA2D and DYNA3D［R］.Army Research Laboratory，Rept.ARL-TR－1310，1997.

［16］石少卿，康建功，汪敏，等.ANSYS／LS-DYNA在爆炸与冲击领域内的工程应用［M］.北京：中国建筑工业出版社，2011.

［17］白金泽.LS-DYNA3D理论基础与实例分析［M］.北京：科学出版社，2005.

［18］卢红琴，刘伟庆.空中爆炸冲击波的数值模拟研究［J］.武汉理工大学学报，2009，31（19）：105－108.

LU Hong-qin，LIU Wei-qing.Research on numerical simulation of blast wave in air［J］.Journal of Wuhan University of Technology，2009，31（19）：105－108.

［19］李顺波，东兆星，齐燕军，等.爆炸冲击波在不同介质中传播衰减规律及数值模拟［J］.振动与冲击，2009，28（7）：115－117.

LIShun-bo，DONG Zhao-xing，QIYan-jun，et al.Numerical simulation on decay spread of blasting shock wave in different media［J］.Journal of Vibration and Shock，2009，28（7）：115－117.

［20］Shi Yan-chao，Li Zhong-xian，Hao Hong.Mesh size effect in numerical simulation of blastwave propagation and interaction with structures［J］.Transactions of Tianjin University，2008，14（6）：396－402.

［21］杨鑫，石少卿，程鹏飞.空气中TNT爆炸冲击波超压峰值的预测及数值模拟［J］.爆破，2008，25（1）：15－18.

YANG Xin，SHI Shao-qing，CHEN Peng-fei.Forecast and simulation of peak overpressure of TNT explosion shock wave in the air［J］.Blasting，2008，25（1）：15－18.

Explosion-resistance behavior and damage assessment of a dup lex hollow CFST column subjected to blast loading

CUIYing1，3，ZHAO Jun-hai2，ZHANG Chang-guang2，SUN Shan-shan2，CHEN Bing1

（1.School of Mechanical Engineering，Xi'an Shiyou University，Xi'an 710065，China；2.School of Civil Engineering，Chang'an University，Xi'an 710061，China；3.School of Aeronautics，Northwestern Polytechnical University，Xi'an 710072，China）

Test analysis and numerical simulationmethod were integrated to evaluate dynamic response and damage of a duplex hollow CFST column subjected to blast loading.A pressure-impulse damage evaluation criterion for the duplex hollow CFST column was defined by analyzing the test data.The results showed that under the blast loading for the test condition of the converted distance of 0.14m／kg1／3，the plastic bending deformation occurs on the surface facing the explosion of the duplex hollow CFST column；the peak pressure in the middle of the column is the highest，the peak pressure at the bottom of the column is higher than that at the top of the column，the latter is the lowest；with the analysis of the duration of the positive pressure，the damage of themiddle of the column is themost serious；so，it is important to coordinate the ends'strength and the whole column's strength in order to enhance the explosion-resistance performance of the duplex hollow CFST column.Finally，a pressure-impulse damage criterion based on the deflection of the fixed-end duplex hollow CFST column was defined，and amathematical formula to generate pressure-impulse diagram（P-I curve）was also established.

explosion mechanics；duplex hollow CFST column；explosion test；numerical simulation；pressureimpulse diagram

TU398+.9

A

10.13465／j.cnki.jvs.2015.21.033

国家自然科学基金项目（41202191）；教育部博士点基金项目（20110205130001）；中国博士后科学基金面上项目（2012M520079、2013T60868）；陕西省自然科学基金项目（2011JM7002）；陕西省教育厅专项科研计划项目（15JK1501）

2014－12－31 修改稿收到日期：2015－03－19

崔莹男，博士后，讲师，1979年生