湍流风场与地震激励联合作用下的风力机结构动力学响应
杨 阳,李 春,2,缪维跑,叶 舟,2,吴 攀
(1.上海理工大学能源与动力工程学院,上海 200093;2.上海市动力工程多相流动与传热重点实验室,上海 200093;3.东方汽轮机有限公司,四川 德阳 618000)
湍流风场与地震激励联合作用下的风力机结构动力学响应
杨 阳1,李 春1,2,缪维跑1,叶 舟1,2,吴 攀3
(1.上海理工大学能源与动力工程学院,上海 200093;2.上海市动力工程多相流动与传热重点实验室,上海 200093;3.东方汽轮机有限公司,四川 德阳 618000)
湍流风场与地震激励是影响风力机安全最主要的客观因素。为分析风力机在湍流风场及地震激励工况下结构动力学响应,以NREL实测数据为湍流风场数据源,结合相干湍流及地震激励,分别研究了多组工况下风轮、塔架和地基的动力学响应。结果表明:湍流风场对叶片载荷、叶尖位移和塔尖载荷影响较大,而地震激励影响可忽略不计;地震激励对地基载荷、地基位移和塔尖位移影响较大,而湍流风场影响可忽略不计;湍流风场与地震激励对塔基载荷均有一定影响,但后者影响更大,二者对风轮推力和功率影响均较大,且处于相同量级;相干湍流与地震激励对塔基载荷和塔尖位移影响相当,可达稳态风的2倍~15倍。
风力机;湍流风场;地震激励;结构动力学
随着化石能源危机日益严重,风能因其资源广泛、利用技术成熟等特点逐渐受到各国重视,2013年世界新增装机容量达到3 546万kW,其中我国占比45.4%[1]。我国风能资源的整体特点是分布广、不稳定和能量密度相对较低[2],风能资源相对丰富的“三北”和沿海地区需要面对地貌复杂、气流强烈的空间不均匀性和时域风场非定常性等客观因素的巨大挑战,强风条件和时有发生的地震均易对风力机造成毁灭性的破坏。因此,对风力机在强风条件下和地震发生时的动力学特性研究已成为当前整机仿真亟需解决的重要课题[3-4]。
风载荷是风力机正常运行时受到的主要载荷,由于未考虑风的强不均匀性及叶片气动弹性响应,叶片在远未达到最大设计风速时就遭到台风破坏[5]。在气动载荷和结构设计中,没有考虑当地风切变等极端风况出现的频率较高的实际情况,仍然使用的是大梁帽设计,屈曲无法满足要求,从而使得风力机叶片遭到破坏[6]。高风速和风速突变等风况下的风力机柔性部件动力学响应研究值得重视。
目前仅考虑风载荷的研究较为多见,但湍流风与地震耦合作用对风力机结构动力学响应研究较少。早期对地震的研究将风轮和机舱简化为塔架顶部的一个质点[7-8],由于这种简化的“堆聚质量”模型无法获知叶片等结构的动力学响应,不能评估叶片所受地震力和塔架-叶片耦合振动效应[9]。地震研究逐渐发展了更高计算精度的模型[10-11],这些模型通过考虑气动力-地震力耦合计算风力机各部件载荷和减少模型简化的方式仿真计算风力机基本震动。
实验和数值计算结果均表明,尤其是对于现代大型风力机的动力学仿真模拟,地震载荷、气动载荷和运行载荷之间的耦合对风力机整机动力学特性影响十分重要[10,12-15]。因此,以NREL5MW陆上风力机[16]为计算样机,耦合地震载荷、气动载荷和运行传动载荷,建立风力机整机动力学仿真模型,以假设模态法计算风力机主要柔性部件的弹性响应。其中,气动载荷计算基于广义动态入流理论,根据模型样机建立相应的风场计算域,在基础流上添加相干结构表示湍动更强烈的拟序结构;地震载荷则参考EICentro地震加速度谱,以响应目标谱的方式转化为地震输入激励,结合DLL控制方法,对风力机模型进行结构动力学仿真,分析风力机各部件动态响应。
1 多体动力学模型及坐标系
1.1 动力学模型
李德源等[17]学者采用超级单元法离散柔性叶片,结合R-W多体动力学分析了叶片在脉冲载荷作用下的动力学响应及频谱,何玉林等[18]通过假设模态法结合Kane方法建模,仿真计算风力机整机结构动态响应。其中,基于Kane方法建模的多体动力学模型将风力机视为具有N个自由度的刚体和柔体结构系统。柔体结构有叶片、传动轴和塔架等,刚性体有地基、轮毂等。
对于风力机整机动力学来说,确定了每个刚体的偏速度和偏角速度,以及相应的广义主动力Fr和广义惯性力之后,其动力学方程[19-22]为:
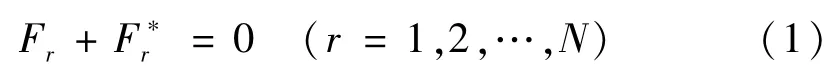
即每个广义速率对应的广义主动力和广义惯性力之和等于零。其中,广义主动力Fr由各部件的重力、气动力、弹性力和其它力组成:

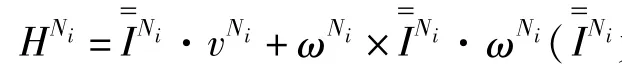
将方程(2)和(3)代入方程(1)中,可得风力机系统动力学方程:
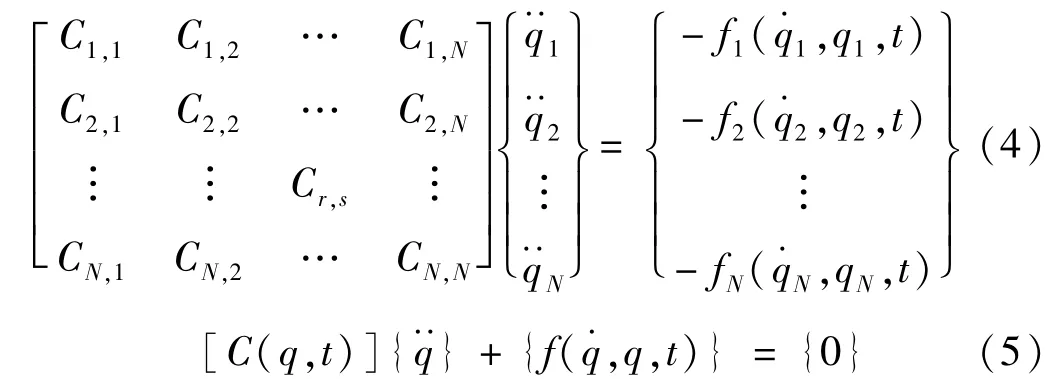
求解各参数时首先通过4阶Adams-Beshforth预测-校正方法确定低阶项的值,并以此构成方程的右边项,然后采用高斯消元法求解系统自由度的加速度。计算得到的加速度值用于修正预测值并以此提高计算精度。迭代数次后采用4阶Adams-Mounton预测-修正算法确定加速度值,并给出该时间步的最终解。由于该算法的非自发性,前4个时间步通过Runge-Kutta法求解。
1.2 风力机坐标系
为方便计算,在风力机上建立多个相对坐标系,分别为叶片坐标系{O,X,Y,Z}、轮毂坐标系{O′,X′,Y′,Z′}、塔架坐标系{O″,X″,Y″,Z″}和地基坐标系{O‴,X‴,Y‴,Z‴},各结构部件自由度示意如图1所示。
2 风模型及气动理论
2.1 风场模型建立

图1 风力机坐标示意图Fig.1 The coordinates of wind turbine
风场模型的选择对仿真结果准确性具有很大影响,为更真实的模拟时域高风速湍流风场及剧烈湍动风场等风况下风力机结构动力学特性,本文选用由NWTC(National Wind Technology Center)建立的NWTCUP谱模型,该模型基于NWTC/LIST项目,由实测40-Hz时间序列数据构成该湍流模型速度谱[2-3],该谱模型通过比例缩放丹麦Risø研究中心开发的SMOOTH模型,缩放系数由具体的风速仪数据确定。此外,在基础流上添加相干结构,以此增加湍流风场的相干湍动能[24],用于描述湍动更为剧烈的拟序结构,其湍流强度为Kelvin-Helmholtz波,相干结构为大涡模拟数值结果,通过一定的比例缩放构成新的风场,相干结构存在时间为总模拟时间的一半,其它时刻与基础湍流风相同,文献[25]有详细的算法介绍。同时,为更好表现湍流风场对风力机结构特性的影响,增加了一个稳态风场,即在模拟时间内风速恒定且没有风切边。以轮毂高度处风速18 m/s参考风速,分别建立了稳态风、湍流风和相干湍流风3种风场,设计风场覆盖区域为180 m×180 m,纵向覆盖了整个风轮和塔架如图2所示。轮毂处时域风速在X′方向分量大小如图3所示。
风剪切效应通过幂律风廓线形式描述,水平方向速度变化规律采用对数风廓线表示:

式中,u(z)为垂直方向速度分布;u(zhub)为轮毂处风速;z为计算节点高度;zhub为轮毂高度;u(y)为水平方向速度分布;u(yhub)为轮毂处风速;y为计算节点水平位置;z0为地表表面粗糙度,其值取0.021;ψ为垂直稳定度无量纲函数。
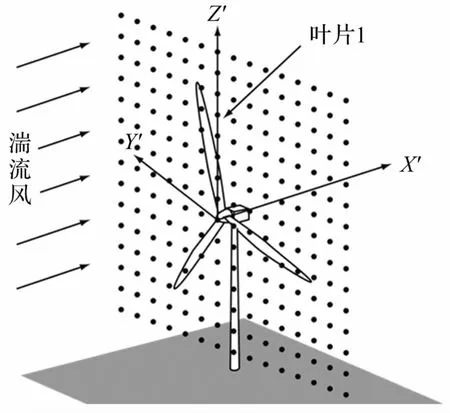
图2 风场计算域示意图Fig.2 Wind Field of Simulation
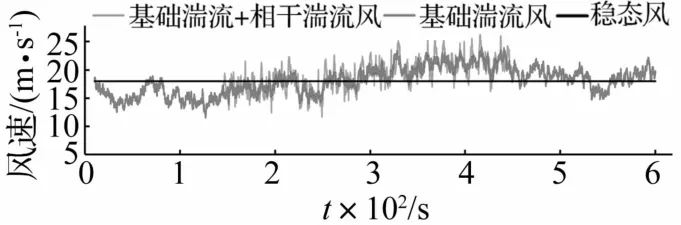
图3 湍流风场和稳态风轮毂高度处风速时域分布Fig.3 Velocities of turbulence wind with coherent structural and steady wind at hub height in time domain
2.2 动态入流理论
风轮气动计算的本质就是利用流体力学控制方程求解流场压力和速度分布规律,基于加速度势的动态入流理论利用分离变量的方法求解Laplace方程表达的压力分布,然后通过Euler方程求解速度分布,结合BEM(Blade Element Moment)理论模型求解风轮气动力。
Pitt-Peters动态入流理论模型通过3个参数描述风轮平面诱导速度变化规律,通过求解诱导速度来获知风轮平面压力分布。式(7)为风轮平面由于扰动引起的诱导速度非均匀分布的一阶Fourier级数表达式。
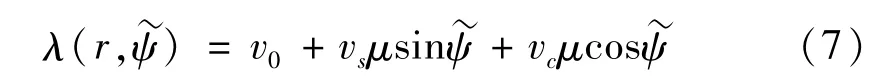
式中,v0、vs、vc分别为诱导速度的平均分布、水平分布和垂直分布;μ为当地半径比;为偏航角。
气动力变化和诱导速度关系为:
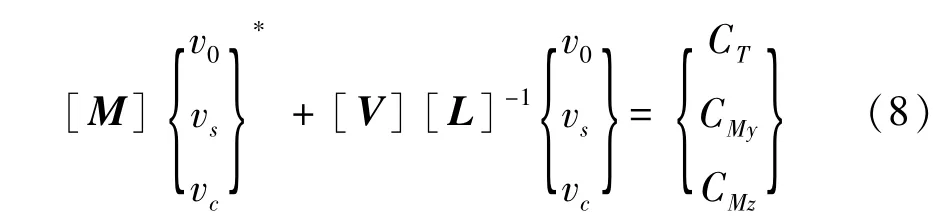
式中,[M]为风轮动态入流的质量矩阵,反映了入流动态特性;[V]为质量流量参数矩阵;[L]为入流增益矩阵;CT、CMy、CMz分别为风轮推力系数、偏航系数和俯仰系数。具体表达式如下:
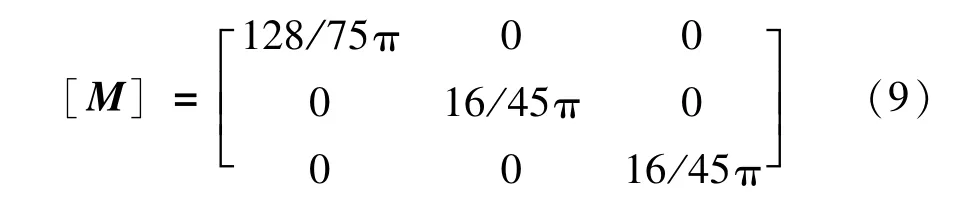
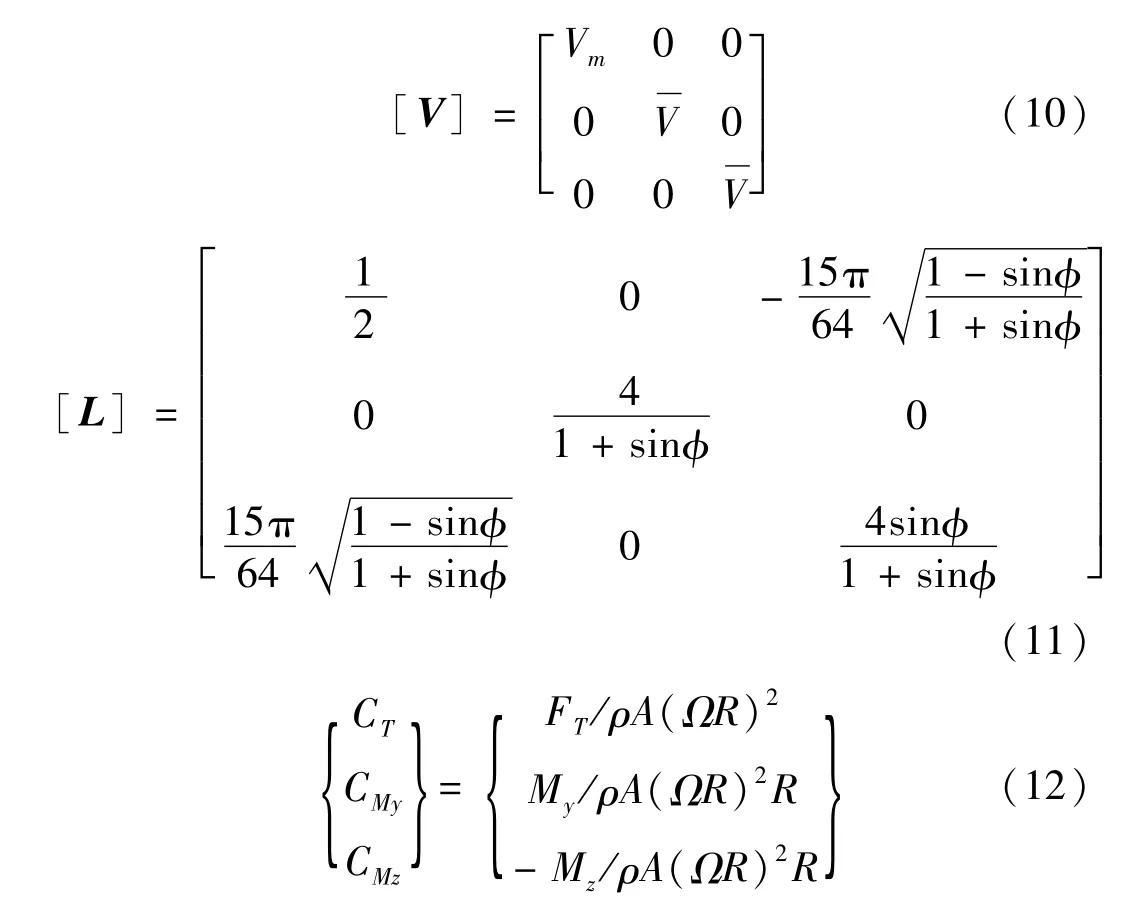
式中,Vm为附加质量流量参数为与时均入流相关的质量流量参数;φ为入流角;FT、My、Mz分别为风轮的推力、偏航力矩和俯仰力矩,其大小通过BEM理论计算得到;Ω、R分别为风轮转速和风轮半径。
通过求解微分方程(8)得到风轮平面诱导速度场,结合相应的翼型空气动力学特性,求解风轮气动力。
3 地震分析模型
地震模拟通常以风力机地基的加速度、速度或位移等运动学特性规律定义地震激励,将地震激励转化为等效的地基载荷并与其他载荷耦合共同作用于风力机。
输入地震激励为EICentro 6.9级地震加速度谱,地震时长约为50 s,在模拟时间第400 s加入,引入零线校正和响应目标谱以增加计算准确性[26-27]。地震加速谱如图4所示。
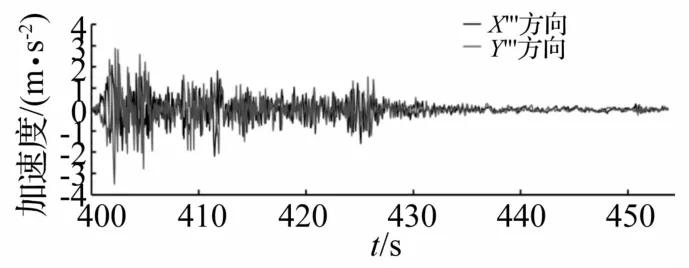
图4 地震加速度谱Fig.4 The acceleration spectrum of seismic
地震载荷计算方法是通过在风力机地基上假设一个阻尼振子,以此得到每一个时间步保持地基预定加速度所需要的地震力,振子刚度k通过式(13)计算:

式中,m为风力机模型总质量,包括地基质量;f为阻尼振子频率,其大小为风力机受激最高频率的10倍,本文取12.5。
假设阻尼振子的阻尼ζ较大[26],此处取ζ=65,同时保持较大的刚度,通过归一化的阻尼值计算阻尼系数c:

因此每一个时间步,地基运动所需的力FP为:

式中dp为地基目标位移,d为地基实际位移;Vp为地基目标速度,V为地基实际速度。
将方程(15)代入方程(2)中,将地震激励嵌入到风力机整机结构动力学方程中,于风载荷共同作用于风力机各结构部件,实现地震与风场耦合影响风力机整机结构特性。
模拟实例原型样机为NREL 5MW风力机,风力机主要参数如表1所示。
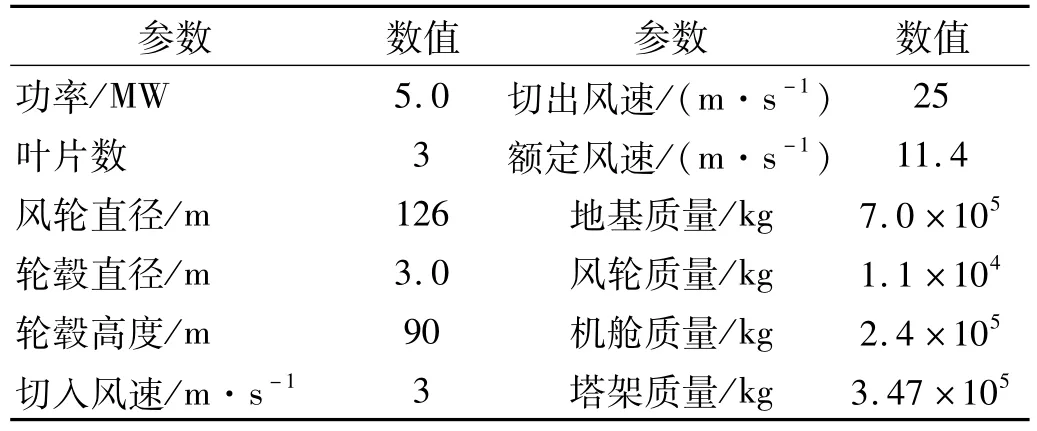
表1 NREL 5MW风力机主要参数Tab.1 The configuration of NREL 5MW w ind turbine
图5为带地震分析模块的整机动力学仿真结构图,其中风力机控制系统和整机载荷之间的耦合通过自编写DLL实现。仿真模拟时间T仿真总时间为600 s,计算时间步长dt为0.005 s。

图5 整机动力学分析系统Fig.5 The system of seismic analysismodel
4 结果与分析
4.1 基础湍流风与地震
风力机的柔性部件主要为叶片、塔架和低速传动轴,其中低速传动轴的刚度相对较大,且在风力机运行过程中位移较小,因此,柔性结构研究重点为叶片和塔架的动态特性。刚性结构主要有地基、轮毂和机舱等,轮毂和机舱受载相对较为稳定,而地基位于地面以下,地震发生时其载荷和位移均发生巨大变化,因此地基为主要研究对象。
首先对比湍流风和地震对风力机各结构部件的动力学响应作用大小,分析了稳态风、基础湍流风和稳态风在第400 s加入50 s地震激励这3种工况。因为未采用独立变桨技术,叶片位移和载荷特性以叶片1为例。图6为叶片1在此3种工况下的载荷和位移动态特性。
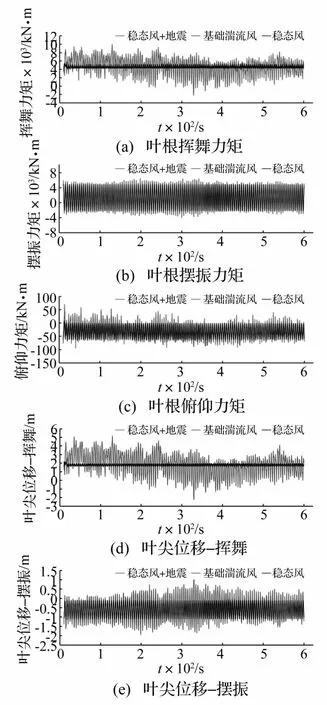
图6 叶片载荷和位移Fig.6 The loads and deflection of the blade
由图6可知,风力机叶片载荷主要受到风载荷影响,在来流风稳定工况下,叶片载荷和位移呈现周期性的变化,且波动较小。
来流风为速度波动较大的湍流风时,叶片三个方向的载荷和位移均呈现较大幅度的无规律波动,其中叶尖挥舞和叶根挥舞力矩变化最剧烈,挥舞力矩此时波动范围为-2.2×103kN·m~1.0×104kN·m,波动幅度达到稳态风的7倍,平均值相等;叶尖挥舞波动范围为-2.23~5.22m,波动幅度为稳态风的14倍,平均值相等。对摆振力矩和叶尖摆振的影响相对较小,俯仰力矩波动幅度值增大了1倍左右。
加入地震激励的稳态风工况与未加入地震激励工况相比,叶片位移和载荷区别不大,在地震激励作用阶段,叶片位移和载荷变化量级与风力机启动时波动相同。相比于湍流风,地震对叶片载荷和位移的影响可以忽略。
图7为3种工况下风轮推力及风轮功率的动态特性。
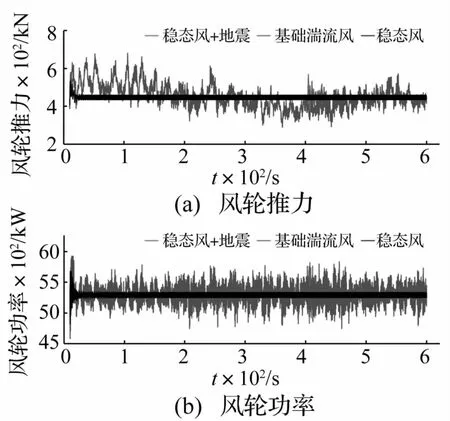
图7 风轮推力和风轮功率Fig.7 Thrust and power of the rotor
由图7可知,稳态风工况下,风力机启动时风轮推力和风轮功率出现幅度较大的波动,但逐渐趋于稳定。
湍流风工况下,风轮推力和风轮功率出现较大波动,其中风轮功率在稳态风时的平均值上下波动,波动幅度较大,最大值为5.93×103kW,最小值为4.58× 103kW。忽略开机启动不稳定工况,其波动范围为稳态风工况的7倍左右。风轮推力波动则相对无规律,波动范围幅度达到稳态风的8倍左右。
加入地震的稳态风工况下,风轮推力和风轮功率均出现幅度巨大的波动,波动规律与地震加速度谱变化规律类似,波动幅度量级与湍流风影响相当。需要注意的是地震激励对风轮推力和风轮功率的影响不可忽略。
图8为3种工况下塔尖载荷和位移的动态特性。
由图8可知,稳态风工况下,塔尖载荷和位移在风力机启动时有较大波动,并逐渐趋于稳定。
来流风为湍流风的工况下,塔尖载荷出现十分剧烈的波动,其中横摇力矩波动幅度相对较小,在-6.67 ×102kN·m~6.16×103kN·m范围内波动,跨度大小为稳态风时的2倍左右,偏航力矩和俯仰力矩的波动幅度值更大,均达到12倍左右。塔尖位移为稳态风时的2倍左右。
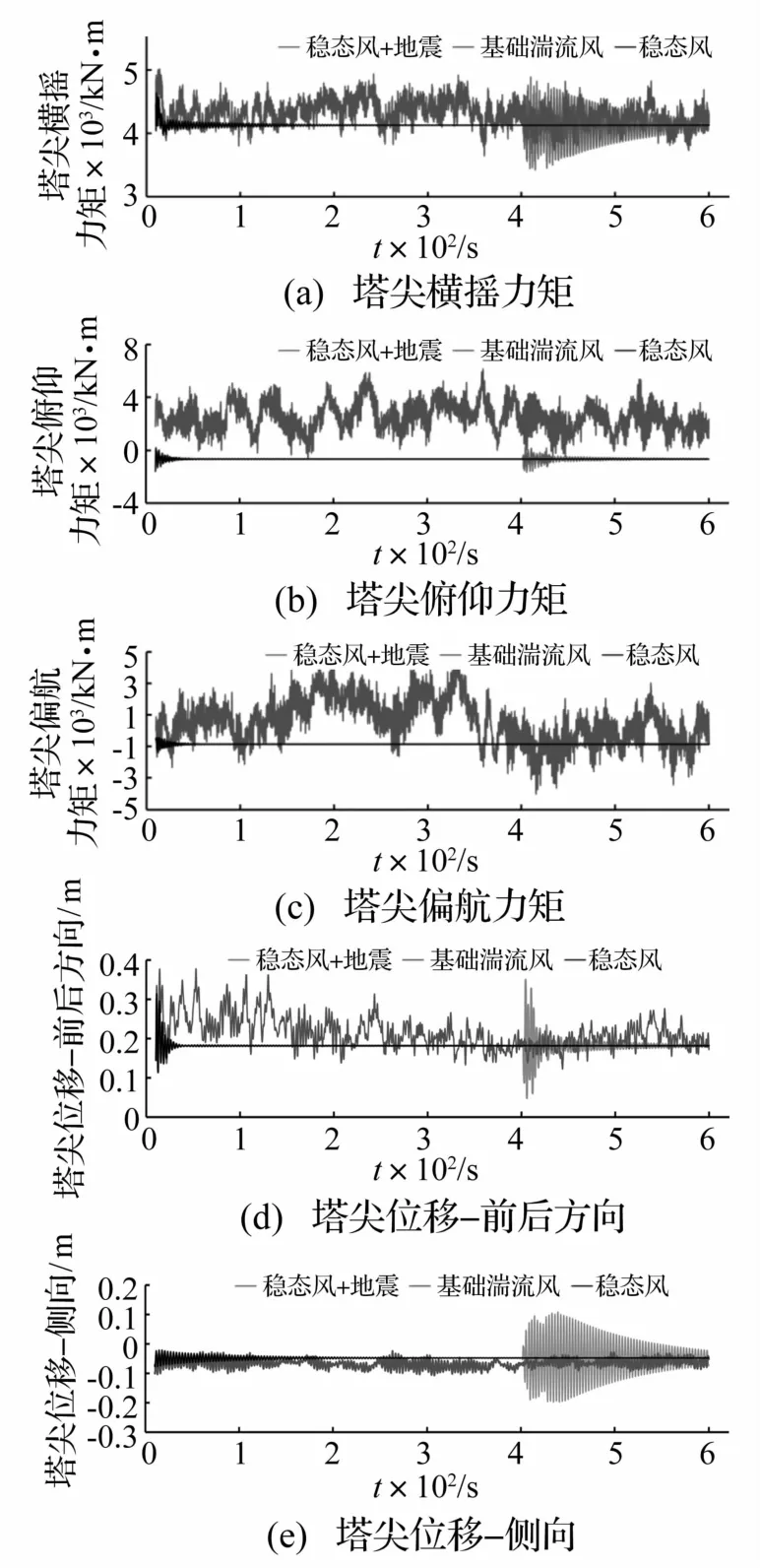
图8 塔尖载荷和位移Fig.8 The loads and deflection of the tower-tip
地震激励对塔尖载荷具有一定影响,其中对横摇力矩达到了湍流风的影响量级,对俯仰力矩和偏航力矩的影响相对较小。地震激励对塔尖位移影响巨大,其中前后方向达到湍流风的影响量级,侧向位移波动比湍流风影响更大,波动范围幅度为湍流风况的3倍左右。
塔尖载荷主要受风场影响,对地震激励敏感性相对较小。塔尖位移主要是前后方向受到风场影响,侧向位移对地震更敏感。
图9为3种工况下塔基载荷和地基位移动态特性。
由图9可知,湍流风载荷对塔基俯仰力矩影响较大,对地基的载荷相对较小。地震载荷对塔架和地基载荷影响巨大,对塔基的横摇力矩达到湍流风最大的6倍,是稳态风的20倍左右。地基载荷对地震激励敏感性较高,地震激励工况下,地基产生的最大剪力达到湍流风况下的30倍以上,地基位移主要受地震激励影响。这是因为质量较大的地基长期处于地面以下,风场对地基的作用力通过塔架传递,因此受到风场的影响有限,地基位移在湍流风和稳态风工况下均为10-5m量级,相比于地震激励的10-1m量级可忽略不计。

图9 塔基载荷和地基载荷及位移Fig.9 Loads of tower-base and the displacement and loads of platform
地基长期位于地面以下,因此,其载荷和位移主要受到地震激励影响。风场对地基的位移和载荷影响可以忽略不计,但对塔基的载荷不可忽略,其量级为地震激励的1/5。
4.2 强湍流风和地震
为进一步研究湍动度更大的风场和地震激励对风力机结构动力学影响程度,在基础湍流风上添加相干湍流以表示湍动剧烈的拟序结构。由上可知,风轮部件动态特性主要受风场影响,地基主要受地震载荷影响。因此,下面主要分析塔架结构在湍流风况与地震耦合作用下的动态特性。对比分析了稳态风、加入相干结构的湍流风和加入地震激励的湍流风这3种工况。
图10为风力机在此3种风况下塔基载荷、塔尖载荷和塔尖位移动态特性。

图10 塔基载荷和塔尖载荷及位移Fig.10 Loads of tower-base and the deflection and loads of tower-tip
由图10可知,湍流风与地震载荷联合作用和拟序结构对塔基载荷的影响相当,均在稳态风工况平均值上下出现较大波动,塔架俯仰力矩波动幅度值达到稳态风工况的2倍左右,巨大的波动会增加塔基的疲劳载荷。横摇力矩波动幅度值达到稳态风工况的15倍,大大的增加了塔架的受载压力。
拟序结构对塔尖载荷影响相较于湍流风与地震激励联合作用更大,对塔尖位移的影响相当。其中,前后方向位移波动幅度值相比于稳态风工况增大3倍左右。
基础湍流风工况下添加相干湍流表示的拟序结构对塔架载荷和位移影响巨大,其影响量级与地震激励相当,设计风力机时应充分考虑相干湍流对塔架载荷和位移的影响。
5 结 论
以NREL 5MW为样机,模拟了风场与地震联合作用多组工况下的结构动力学动态响应,分析了风力机主要柔性部件和地基的动力学时域响应,主要得到以下结论:
(1)风力机叶片载荷和位移主要受风场影响,在来流湍动剧烈时,叶尖位移呈现无规律的大幅波动,其中挥舞方向位移受影响最大,本文选取湍流风场模型使叶尖挥舞最大位移增大3倍左右。相比于湍流风,地震激励对叶片载荷和位移的影响可忽略不计。
(2)湍流风对风轮推力和风轮功率有较大影响,与地震激励影响量级相当。
(3)地震激励和湍流风工况均会使塔尖载荷和位移出现较大波动,其中俯仰力矩和偏航力矩主要受风场作用,塔尖位移主要受地震载荷影响。
(4)塔基和地基的载荷与位移主要受到地震激励影响,湍动风场对塔基载荷有一定影响,但小于地震激励影响。湍动风场对地基的载荷相对于地震激励可以忽略不计,对地基位移几乎没有影响,远小于地震激励对地基的影响。
(5)在基础湍流风工况下添加相干湍流,加剧了风湍动,拟序结构与湍流风工况下的地震激励对塔基载荷影响相当,均达到稳态风工况下的2~15倍。剧烈的风湍动使得塔尖位移与地震激励相当。
[1]GWEC.Global Wind Statistics 2013[C]//Brussels,Belgium,2014.
[2]李春,叶舟,高伟,等.现代陆海风力机计算域仿真[M].上海:上海科学技术出版社,2012.
[3]Bhattacharya S,Nikitas N,Garnsey J,et al.Observed dynamic soil-structure interaction in scale testing of offshore wind turbine foundations[J].Soil Dynamics and Earthquake Engineering,2013,54:47-60.
[4]Ding Jie,Chen Xin-zhong.Assessing small failure probability by importance splitting method and its application to wind turbine extreme response prediction[J].Engineering Structures,2013,54:180-191.
[5]王景全,陈政清.试析海上风机在强台风下叶片受损风险与对策——考察红海湾风电场的启示[J].中国工程科学,2010,12(11):32-34.
WANG Jing-quan,CHEN Zheng-qing.Analysis of risk and measures on the blade damage of offshorewind turbine during strong typhoons—enlightenment from red bay wind farm[J].Engineering Sciences,2010,12(11):32-34.
[6]宋丽莉,毛慧琴,钱光明,等.热带气旋对风力发电的影响分析[J].太阳能学报,2006,27(9):961-965.
SONG Li-li,MAO Hui-qin,QIAN Guang-ming,et al.Analysis on the wind power by tropical cyclone[J].Acta Energiae Solaris Sinica,2006,27(9):961-965.
[7]Bazeos N,Hatzigeorgiou G D,Hondros ID,et al.Static,seismic and stability analyses of a prototype wind turbine steel tower[J].Engineering Structures,2002,24(8):1015-1025.
[8]Lavassas I,Nikolaidis G,Zervas P,et al.Analysis and design of the prototype of a steel1-MW wind turbine tower[J]Engineering Structures,2003,25(8):1097-1106.
[9]范洪军,金全洲,刘铁英,等.风力机地震响应分析的研究现状与展望[J].结构工程师,2010,26(6):155-163.
FAN Hong-jun,JIN Quan-zhou,LIU Tie-ying,etal.State ofthe art In seismic response analysis of wind turbines[J].Structural Engineers,2010,26(6):155-163.
[10]Witcher D.Seismic analysis of wind turbines in the time domain[J].Wind Energy,2005,8(1):81-91.
[11]Prowell I,Elgamal A,Romanowitz H,et al.Earthquake responsemodeling for a parked and operating megawatt-scale wind turbine[R].National Renewable Energy Laboratory,2010,NREL/TP 5000-48242.
[12]Prowell I,An experimental and numerical study of wind turbine seismic behavior[D].California,University of California,2011.
[13]Zhao X.Maisser P.Seismic response analysis ofwind turbine towers including soil-structure interaction[J].Journal of Multi-Body Dynamics,2006,220(1):53-61.
[14]Haenler M,Ritschel U,Warnke I.Systematic modelling of wind turbine dynamics and earthquake loads on wind turbines [C]//European Wind Energy Conference and Exhibition.European Wind Energy Association:Brussels,Belgium,2006.
[15]Ishihara T,Sawar M W.Numerical and theoretical study on seismic response of wind turbines[C]//European Wind Energy Conference and Exhibition.European Wind Energy Association:Brussels,Belgium,2008.
[16]Jonkman J,Butterfield S,MusialW,et al.Definition of a 5 -MW reference wind turbine for offshore system development[R].National Renewable Energy Laboratory,2009,NREL/TP 500-38060.
[17]莫文威,李德源,夏鸿建,等.水平轴风力机柔性叶片多体动力学建模与动力特性分析[J].振动与冲击,2013,32 (22):99-105.
MO Wen-wei,LI De-yuan,XIA Hong-jian,et al.Multibody dynamic modeling and dynamic characteristic analysis of flexible blades for a horizontal axis wind turbine[J].Shanghai:Journal of Vibration and Shock,2013,32(22):99-105.
[18]王磊,陈柳,何玉林,等.基于假设模态法的风力机动力学分析[J].上海:振动与冲击,2012,31(11):122-126.
WANG Lei,CHEN Liu,HE Yu-lin,et al.Dynamic analysis of awind turbine base on assumedmodemethod[J].Shanghai:Journal of Vibration and Shock,2012,31(11):122 -126.
[19]刘延柱,洪嘉振.多刚体系统动力学[M].北京:高等教育出版社,1989.
[20]洪嘉振.计算多体系统动力学[M].北京:高等教育出版社,1999.
[21]刘桦.风电机组系统动力学模型及关键零部件优化研究[D].重庆:重庆大学,2009.
[22]Jonkman JM.Modeling of the uaewind turbine for refinement of FAST_AD[R].National Renewable Energy Laboratory,2003,NREL/TP 500-34755.
[23]Kelly N D,Shirazi M,Jager D,et al.Lamar low-level jet project interim report[R].National Renewable Energy Laboratory,2004,NREL/TP-500-34593.
[24]Kelley N D,Jonkman B J,Scott G N,et al.The impact of coherent turbulence on wind turbine aeroelastic response and its simulation[R]National Renewable Energy Laboratory,2005,NREL/CP-500-38074.
[25]吴攀,李春,李志敏,等.风力机不同风况的动力学响应研究[J].北京:中国电机工程学报,2014,26(34):4539-4545.
WU Pan,LIChun,LIZhi-min,et al.Research on dynamic characteristics simulation for wind turbine with different wind [J].Beijing:Proceedings of CSEE,2014,26(34):4539-4545.
[26]Naeim F.Dynamics of structures-theory and applications to earthquake engineering[J].Earthquake Spectra,2007,23 (2):491-492.
[27]Atik L A.Abrahamson N.An improved method for nonstationary spectral matching[J].Earthquake Spectra,2010,26(3):601-617.
[28]Prowell I,Elgamal A,Uang C,et al.Estimation of seismic load demand for a wind turbine in the time domain[R].Report No.NREL/CP 500-47536,2010.
Structural dynam ic responses of a w ind turbine under turbulent w ind combined w ith seism icmotion
YANG Yang1,LIChun1,2,MIAOWei-pao1,YE Zhou1,2,WU Pan1
(1.School of Energy and Power Engineering,University of Shanghai for Science and Technology,Shanghai200093,China;2.Shanghai Key Laboratory of Multiphase Flow and Heat Transfer in Power Engineering,Shanghai200093,China;3.Dong Fang Turbine Co.,LTD,Deyang 618000,China)
Turbulent wind field and seismic excitation are the leading objective factors affecting the operational safety of a wind turbine.In order to analyze the structural dynamic response of a wind turbine under turbulent wind and seismicmotion,NRELmeasured data were taken as the source of turbulentwind field to combine coherent turbulent and seismicmotion,the dynamic response of the rotor,tower and platform of thewind turbinewere studied,respectively.The results showed that the turbulentwind has a bigger impact on loads and deflections of blades,and loads at the tower-tip,while the influence of seismicmotion can be ignored;the seismic excitation has a larger impact on loads and displacements of platform,and deflection at the tower-tip,while the influence of turbulentwind can be ignored;the turbulentwind and seismic motion both have a certain impacton loads of tower-base,the coherent turbulent and seismicmotion have the same impact on loads of tower-base and deflection of tower-tip,their amplitudes can reach 2-15 times of those under stationary wind.
wind turbine;turbulentwind field;seismicmotion;structural dynamic characteristics
TK83
A
10.13465/j.cnki.jvs.2015.21.024
国家自然科学基金资助项目(E51176129);上海市教育委员会科研创新(重点)项目(13ZZ120,13YZ066);教育部高等学校博士学科点专项科研基金(博导类)项目(20123120110008);上海市研究生创新基金项目(JWCXSL1402)
2014-10-10 修改稿收到日期:2014-11-11
杨阳男,硕士生,1992年8月生
李春男,博士,教授、博士生导师,1963年2月生

