考虑需求者期望的两阶段医疗服务供需匹配方法
王 娟,陈 希,赵 柳
(西安电子科技大学经济与管理学院,陕西 西安 710071)
1 引言
随着人口老龄化以及社会经济的发展,将带来医疗服务需求的大幅度增长。在这样的背景下,如何吸引医疗服务需求者,提高医疗机构的服务质量和市场竞争力,对于需求者获得更优质的医疗服务以及医疗机构未来的发展具有十分重要的意义。因此,如何将医疗服务供需双方进行有效匹配,从而提高医疗效率和服务需求者的满意度是值得关注的重要问题。在匹配决策过程中,主体往往是有限理性的[1],主体的需求和期望也应被考虑[2]。因此,医疗机构在匹配供需双方时,应该考虑需求者的期望与需求,以提高需求者的满意度和忠诚度。而在现有的医疗服务研究中[3-5],医疗机构对服务需求者的安排往往不考虑其需求和期望。同时面对大量的医疗服务需求,如何依据需求者的情况和期望,合理、有效地将需求者分组并分配给相应的供给者,使需求者能及时得到医疗服务且满意度最高,是一个具有实际价值的研究问题。目前,关于医疗服务需求者分组问题的研究所见不多,而分组的方法已经应用在多个领域[6-8],如专家分组问题[6]、应急救援分组问题[7]等。已有研究[8-9]为研究服务需求者的分组提供了思路和方法,如Jabeur[9]等提出了一种根据个体方案偏好,考虑各方案之间的相对重要性进而对多个方案进行分类的群决策方法。因此,针对上述问题,本文提出了一种考虑医疗服务需求者期望的两阶段供需匹配方法。在第一阶段,根据相应的原则并考虑需求者期望之间的相似性,将需求者均衡分组。第二阶段,根据每组需求者对供给者的满意度,得到需求者与供给者之间的匹配结果。
2 问题描述
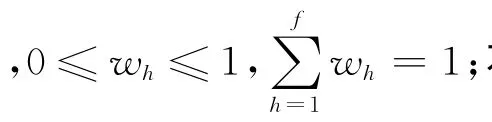
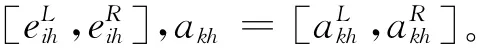
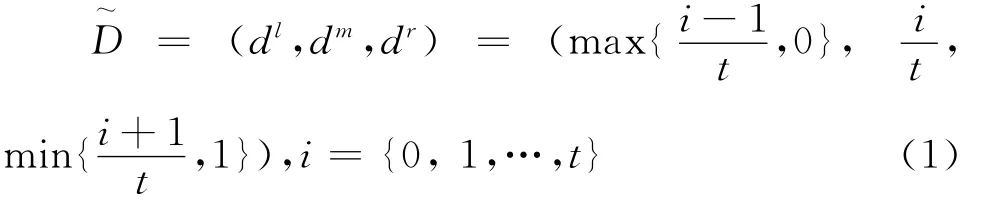
根据式(1)将需求者的期望值和供给者的评价值中指标值为语言短语的值转换为三角模糊数,即将eih和akh转化为
本文要解决的问题是:根据需求者对供给者的期望信息,提出了一种两阶段的医疗服务供需匹配方法,第一个阶段,将需求者均衡地分为若干小组;第二个阶段,将需求者的分组和供给者进行匹配。
3 模型的构建
3.1 需求者的分组
不同的需求者对供给者的期望不同,将期望相似的需求者进行均衡分组,可有效缩短医疗服务安排的时间,并可使需求者满意度达到最高。分组时,首先要得到需求者之间期望的相似度。在指标Ch下,需求者Di和Dj对供给者期望之间的距离为:
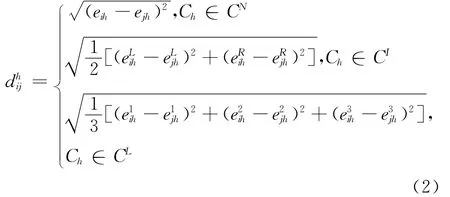
为消除不同量纲对计算结果的影响,将距离规范化为,有:
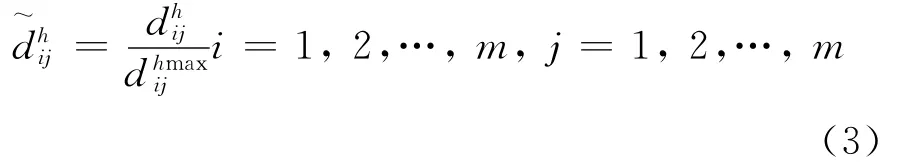
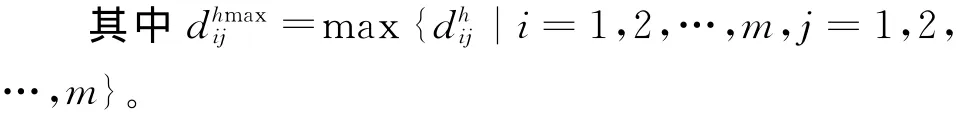
需求者Di和Dj期望之间的距离为:
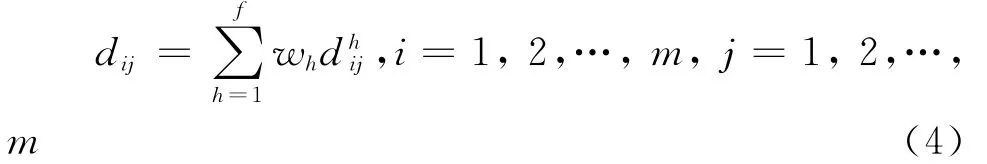
建立医疗服务需求者Di和Dj对供给者期望之间对称的相似度矩阵S=[sij]m*m,其中:
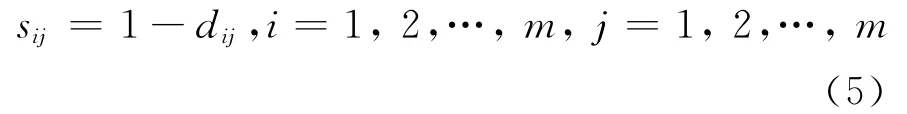
在对需求者进行分组时,不仅要考虑需求者的期望,供给者的工作时间和工作强度也应该被考虑,各个供给者的工作强度应尽量均衡。因此,分组时需要遵循以下5个规则:
规则1:每组需求者对供给者的期望尽量相似。
规则2:各组需求者的人数应尽可能相同。
规则3:各组需求者病情严重程度应尽量均衡。
规则4:各组需求者的总治疗时间应尽量相同。
规则5:每个需求者必须并且只能被分到一个组中。
记T表示服务供给者每天的工作时间;pi反映了需求者Di病情的严重程度,本文pi的值取1、2、3,pi=1表示病情较轻,pi=2表示病情一般,pi=3表示病情严重;ti表示需求者Di的治疗时长;代表各组之间需求者人数的差异,代表各组之间需求者整体病情严重程度的差异,代表各组之间需求者总治疗时间之间的差异。ω1、ω2和ω3分别表示的权重;设模型的决策变量为

另外,xjg与xil的定义与上述相同,均为0-1决策变量。根据相似度矩阵S,建立医疗服务需求者分组问题的多目标优化模型为:
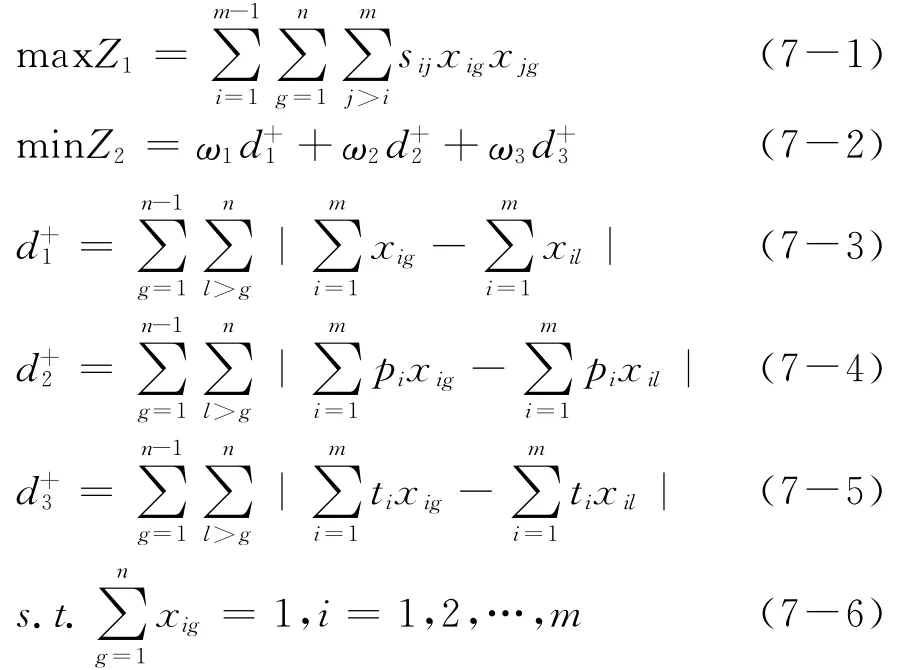
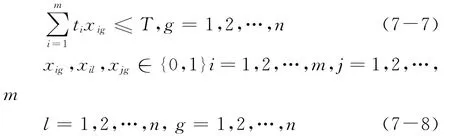
上述模型中,式(7-1)和(7-2)为目标函数,分别表示极大化每组内医疗服务需求者期望的相似度和极小化各组之间需求者的总人数、整体病情严重程度与总治疗时间三部分差异的加权和;约束条件(7-6)限制每个需求者只能被分配给一个供给者;约束条件(7-7)确保每个供给者对该组需求者的治疗时间总和在规定的工作时间范围内。
为求解上述多目标优化模型,采用隶属度函数的加权和方法进行处理[11]。设分别为单独考虑目标Z1和目标Z2优化时所获得的最小值,而分别为相应的最大值,则两个目标函数式(7-1)和式(7-2)的隶属度函数可分别定义为:
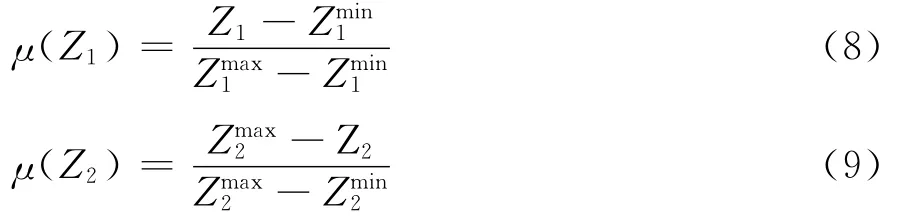
设v1和v2分别为目标函数Z1和Z2的权重,采用线性加权法[12]将两个目标的隶属度函数加权并建立一个新的单目标函数为:
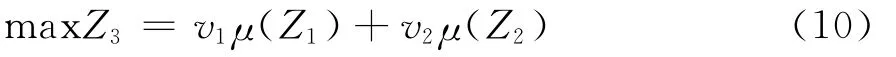
3.2 医疗服务供需匹配方法
在进行医疗服务供需匹配时,首先要比较每组需求者的期望值和供给者的实际评价值之间的差异,得到每组需求者对供给者的满意度,具体方法如下:
(1)当Ch∈CN时,分组Bg的指标Ch期望值的均值为:
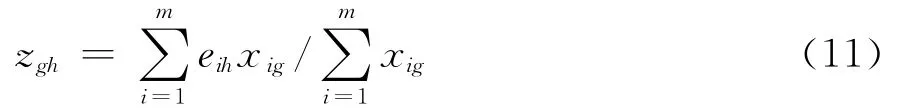
设ahmin表示指标Ch下所有医疗服务供给者评价值的最小值,ahmax表示最大值。则在指标Ch下,供给者的评价值akh和分组Bg中的需求者的期望均值zgh之间差异度为:
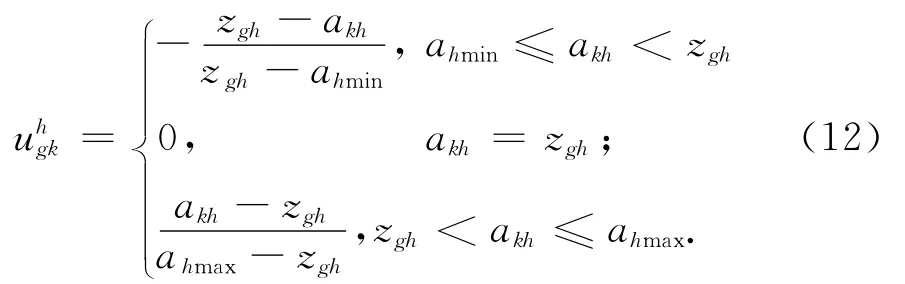
(2)当Ch∈CI时,分组Bg的指标Ch期望值的均值可表示为:其中:
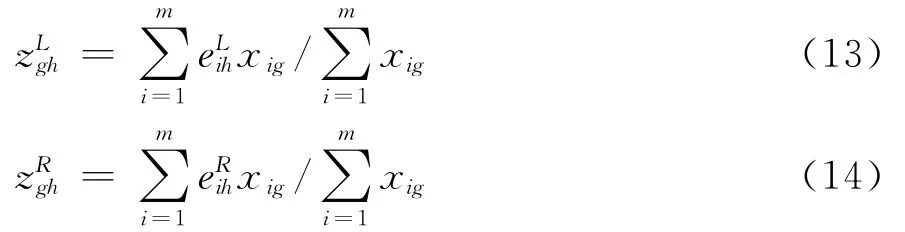
设ahmin表示指标Ch下所有医疗服务供给者评价值下限中的最小值,ahmax表示评价值上限中的最大值。则在指标Ch下,供给者的评价值akh和分组Bg中的需求者的期望均值zgh之间差异度为:

(3)当Ch∈CL,令αih表示期望值eih对应的语言变量的下标值,分组Bg的指标Ch期望值的均值为:
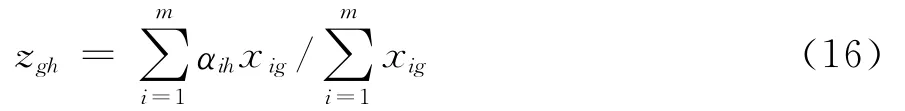
设βkh表示评价值akh的语言变量的下标值,βhmin表示βkh的最小值,βhmax表示βkh的最大值。则在指标Ch下,供给者的评价值akh和分组Bg中的需求者的期望均值zgh之间差异度为:
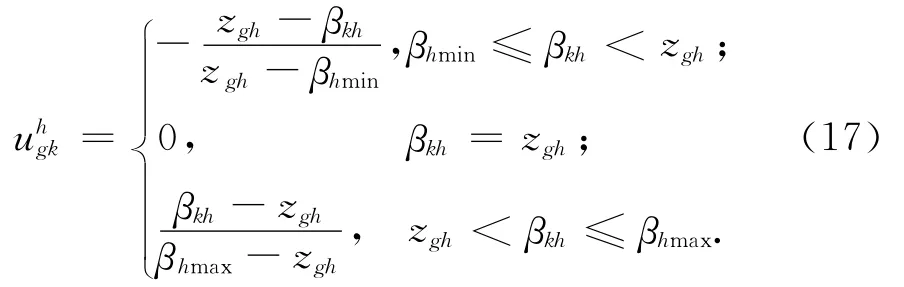
分组Bg中的需求者对供给者Sk的满意度为:

根据获得的每个分组需求者对供给者的满意度Ugk,建立以需求者满意度最大为目标的优化模型。引入0-1变量ygk,ygk=1表示分组Bg的需求者和供给者Sk匹配,ygk=0表示分组Bg的需求者和供给者Sk不匹配。根据满意度Ugk,建立如下优化模型:
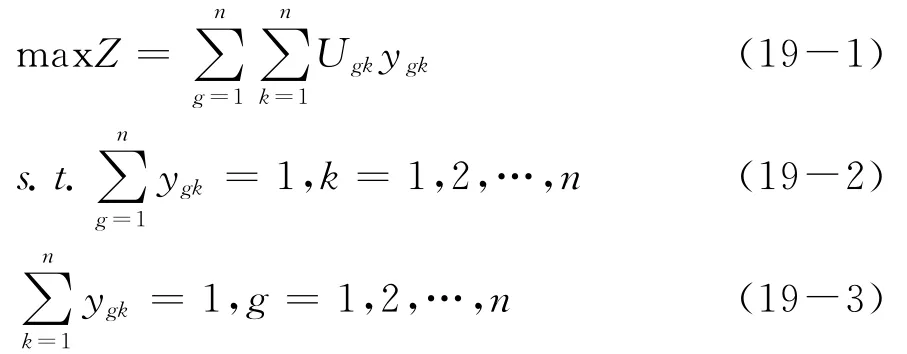
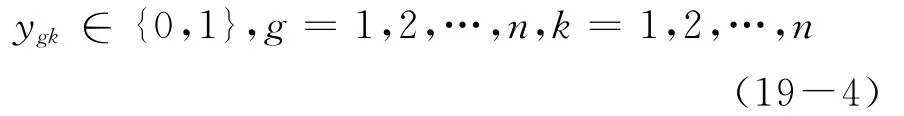
其中,式(19-1)为目标函数,表示医疗服务需求者的满意度最大;式(19-2)为约束条件,表示每一个供给者只能匹配一组需求者。式(19-3)为约束条件,表示每一组需求者只能匹配一个供给者。
式(10)和式(19)可使用优化软件包或遗传算法编程等方法求解。
4 算例分析
西安市某一所医院中,有10个病人D={D1,D2,…D10}预约星期四的康复治疗,该医院有三个康复治疗的医生S= {S1,S2,S3}。病人在预约医生时主要考虑的指标为专业程度(C1,单位分)、收费(C2,单位元)、声誉(C3)和治疗水平(C4)。决策者给出的 各 指 标 的 权 重 为W= (0.32,0.12,0.21,0.35)。病人对医生的期望水平如表1所示,医生实际评价信息如表2所示。
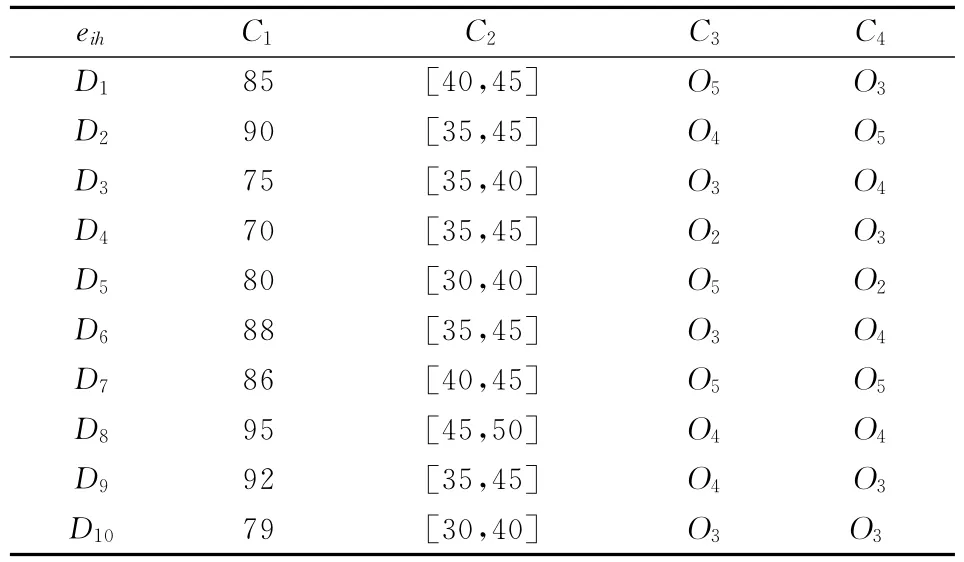
表1 病人对医生的期望信息
病人病情的严重程度pi和所需的治疗时间ti如表3所示。为解决病人之间分组的问题,首先将C3、C4的指标值转换为三角模糊数,然后根据式(2)比较不同形式下指标之间的距离,由式(3)~(5)得到病人之间期望的相似度矩阵S= [sij]m*m,结果如表4所示(结果保留4位有效数字)。
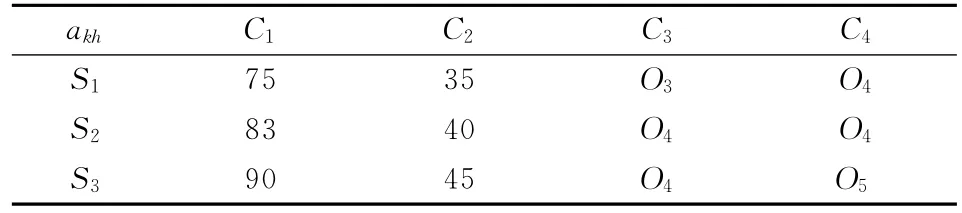
表2 医生的实际评价信息
根据分组结果,利用式(11)~(17)得到各指标下供给者的评价值和各分组的需求者的期望值之间差异度,利用式(18)计算得到每个分组对服务供给者的满意度,结果如表5所示(结果保留4位有效数字)。
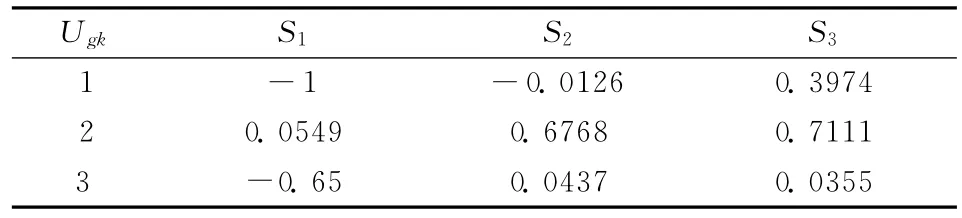
表5 每个分组对服务供给者的满意度
根据满意度,利用式(19)建立单目标的优化模型,使用Lingo 10求解模型,得到的结果如下:x11=0。
根据得到的相似度矩阵,利用式(7)建立多目标优化模型,其中,ω1= 0.279、ω2= 0.344、ω3=0.377,将模型转化为单目标优化模型,v1=v2=0.5。通过Lingo 10求解,得到如下结果:x11=1,x12=0,x13=0,x21=0,x22=0,x23=1,x31=0,x32=1,x33=0,x41=0,x42=1,x43=0,x51=1,x52=0,x53=0,x61=0,x62=1,x63=0,x71=1,x72=0,x73=0,x81=0,x82=0,x83=1,x91=0,x92=0,x93=1,x101=0,x102=1,x103=0。即B1组包括D1、D5和D7,B2组包括D3、D4、D6和D10,B3组包括D2、D8和D9。

表3 病人的病情及所需治疗时间
x12=0,x13=1,x21=1,x22=0,x23=0,x31=0,x32=1,x33=0。则将分组B1和医生S3相匹配,将分组B2和医生S1相匹配,将分组B3和医生S2相匹配。
5 结语
本文针对医疗服务的供需匹配问题,考虑服务需求者的期望,提出了一种两阶段的决策方法。该方法具有逻辑清晰、计算简单等特点。在第一个阶段,根据需求者的期望之间的相似度以及相应的规则,通过建立优化模型,将需求者进行合理的分组。在此基础上,根据每组需求者对供给者的满意度,建立优化模型,获得需求者分组和供给者之间的匹配结果。后续的研究可以分析医疗服务中供需双方其他的心理行为,而更有效的供需匹配方法也是值得进一步研究的方向。
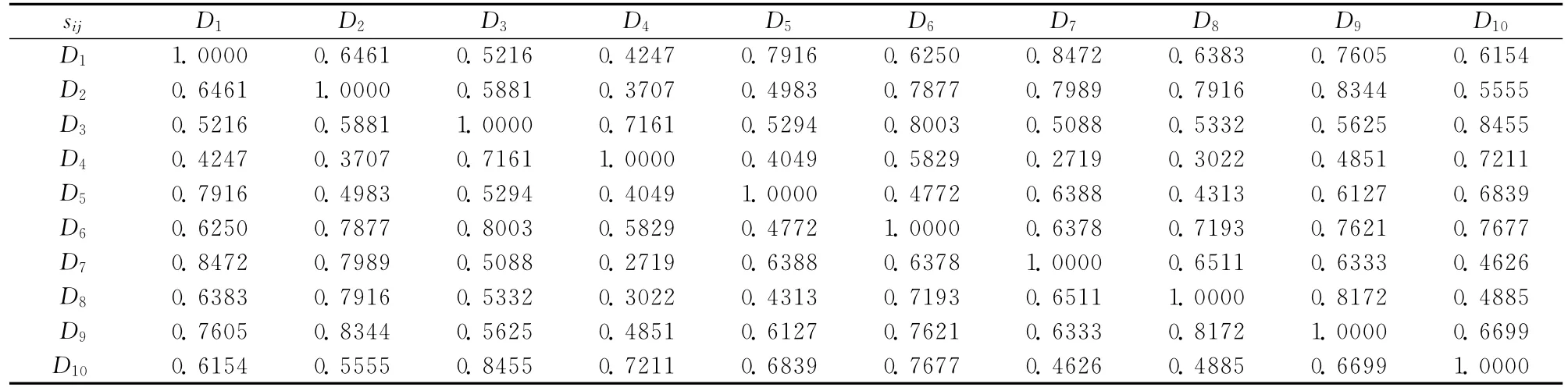
表4 病人之间期望的相似度
[1]Kahneman D,Tversky A.Prospect theory:An analysis of decision under risk[J].Econometrica,1979,47(4):263-91.
[2]Nowak M.Aspiration level approach in stochastic MCDM problems[J].European Journal of Operational Research,2007,177(3):1626-1640.
[3]Chang C S,Chen S Y,Lan Yiting.Service quality,trust,and patient satisfaction in interpersonal-based medical service encounters[J].Bmc Health Services Research,2013,13(2):653-653.
[4]Lotfi V,Torres E.Improving an outpatient clinic utilization using decision analysis-based patient scheduling[J].Socio-Economic Planning Sciences,2014,48(2):115-126.
[5]Zhu Jianan.Income,demand and market equilibrium of the high level medical and health service:A sample of Hangzhou[J].Information Technology Journal,2013,12(17):4127-4131.
[6]Chen Yuan,Fan Zhiping,Ma Jian,et al.A hybrid grouping genetic algorithm for reviewer group construction problem[J].Ex-pert Systems with Applications,2011,38(3):2401-2411.
[7]樊治平,刘洋,袁媛,等 .突发事件应急救援人员的分组方法研究[J].运筹与管理,2012,21(2):1-7.
[8]Brimberg J,Mladenovic'N,Uroševic'D.Solving the maximally diverse grouping problem by skewed general variable neighborhood search[J].Information Sciences,2015,295(4):650-675.
[9]Jabeur K,Martel J.An ordinal sorting method for group decision-making[J].European Journal of Operational Research,2007,180(3):1272-1289.
[10]Li Rongjun.Fuzzy method in group decision making[J].Computers & Mathematics with Applications,1999,38(1):91-101.
[11]Chen Y W,Wang C H,Lin S J.A multi-objective geographic information system for route selection of nuclear waste transport[J].Omega,2008,36(3):363-372.
[12]Roth A E.The evolution of the labor market for medical interns and residents:a case study in game theory[J].The Journal of Political Economy,1984,92(6):991-1016.

