一类具有饱和发生率的病毒感染模型的稳定性分析∗
吴朝彪,夏米西努尔阿布都热合曼
(新疆大学数学与系统科学学院,新疆乌鲁木齐830046)
0 引言
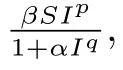
1 基本性质
本文在文献[8]模型下做出一些改变,研究如下一般非线性病毒发病感染率的xyv模型,其中x(t),y(t),v(t)分别代表t时刻宿主体内未感染细胞数量、感染细胞数量和游离病毒的数量,则可得到带有饱合发生率的病毒感染数学模型
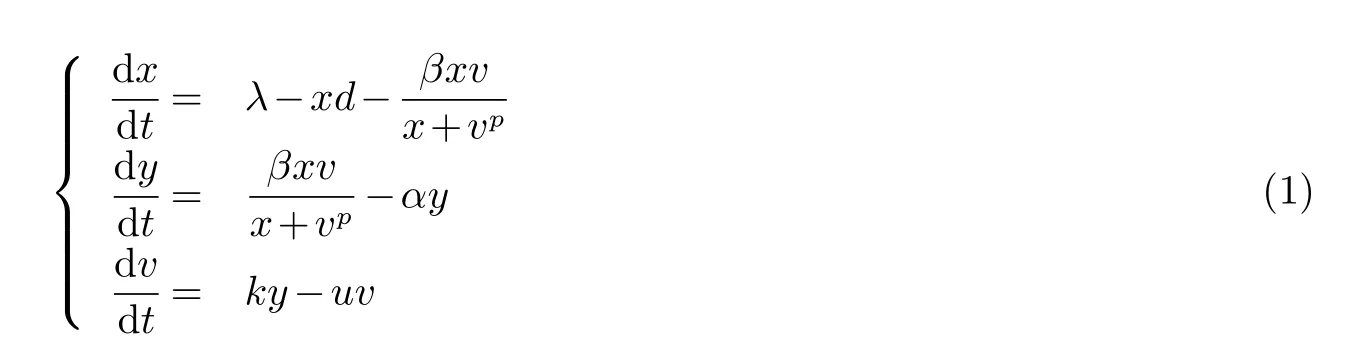
其中参数λ表示未感染细胞在人体组织中的常数产生率;d表示未感染细胞的死亡率,α表示感染细胞的死亡率,u表示游离病毒的死亡率表示游离病毒接触并成功感染未感染细胞的速率;k是指感染细胞释放游离病毒的速率.
模型(1)的初始条件为

系统(1)有一个无感染平衡点令基本再生数取为
引理1若R0≥1,即则系统(1)存在唯一的持续带毒平衡点其中

而v∗满足下面的方程(4)
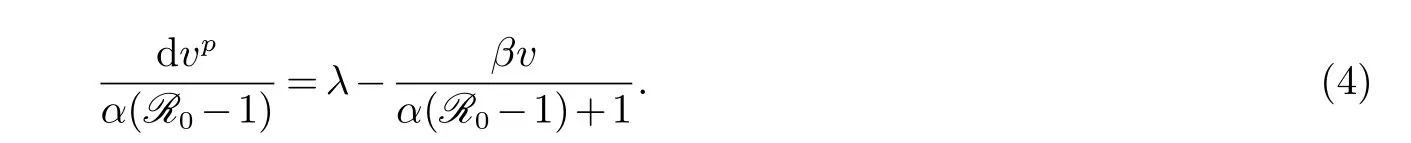
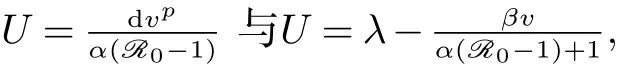
引理2设(x(t),y(t),v(t))是模型(1)满足初始条件(2)的解,则对任意的t≥0,解(x(t),y(t),v(t))是正的.
证明假设x(t)在(0,)内不恒大于0,则存在>0,使得(x(t)>0),t∈(0,)但是x()=0,对于t∈(0,),从而有令由于x(t)连续,则
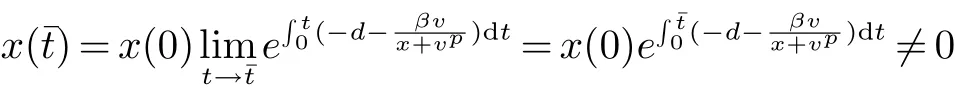
矛盾,所以x(t)>0,t>0,类似于x(t)正性的证明,可以得到y(t),v(t))的正性.
引理3对系统(1)满足初始条件(2)的任意解(x(t),y(t),v(t))是有界的.
证明令N(t)=x(t)+y(t),m=min(d,α),则故,x(t),y(t)有界,由系统(1)的第三个方程知v(t)也有界,即存在M使得
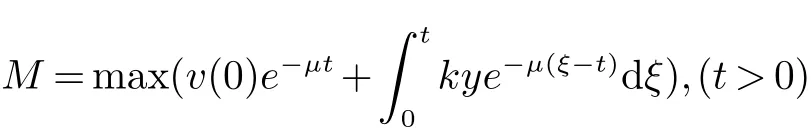
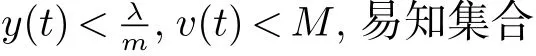
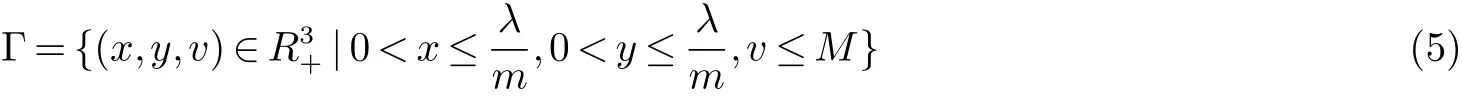
是系统(1)的正向不变集:
2 无感染平衡点的全局动力学
在本节中,假设R0≤1,并构造Lyapunov函数,得出模型(2)的无感染平衡点是全局渐近稳定的.
定理1当R0<1时,系统(1)的无病平衡点是全局渐近稳定的.
证明首先证明系统无病平衡点E0的局部稳定性.系统(1)的Jacobian矩阵为
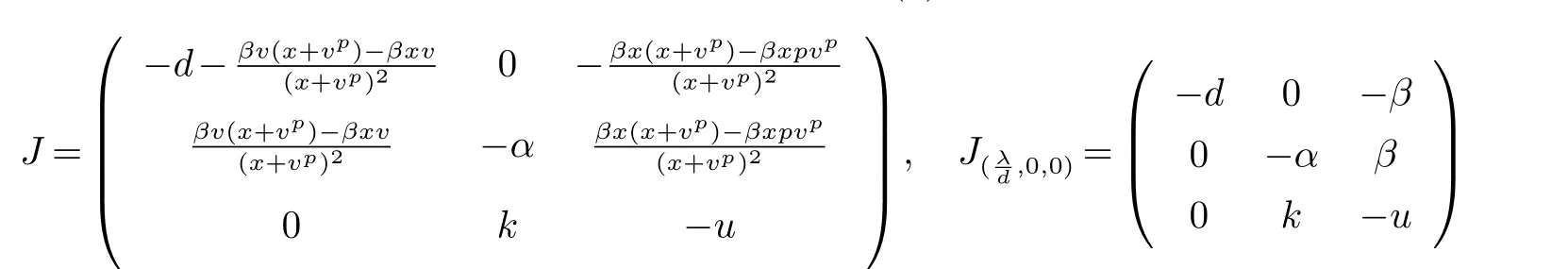
它有三个特征根分别为
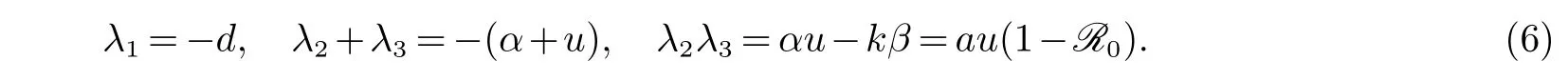
故当时无病平衡点是局部稳定的,当Ro>1时,是不稳定的.
下面证明当R0<1时,是全局吸引的.构造Lyapunov函数如下

记:
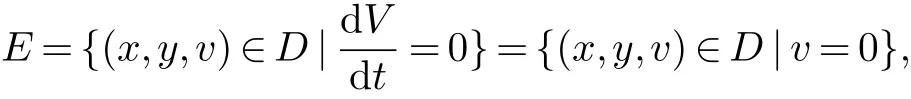
容易看出,系统(1)在E中的最大不变集M只有唯一的点由LaSalle不变性原理及极限方程理论可知是全局吸引的,结合E0的局部稳定性可知,当R0<1时,E0全局渐近稳定.
3 持续带毒平衡点的全局稳定性
本部分利用Bendixson判据方法[9]分析持续带毒平衡点的全局稳定性.
设开集D⊂Rn,对x7→f(x)∈Rn是C1类函数,考虑微分方程

设x(t,x0)是方程(8)满足条件x(t,x0)=x0的解.集合K被称为方程(8)在D内的吸引集,若对每一个紧子集K1⊂D,当t充分大时,都有x(t,K1)⊂K.给出基本假设:
(H1)方程˙x=f(x)在D内存在一个紧吸引子集K⊂D,
(H2)方程˙x=f(x)在D内存在唯一平衡点¯x⊂D.
有如下Bendixson判据定理,参看[9]的定理2.3.文献[9]显示,如果D是单连通的,条件q<0能排除系统出现任何闭轨道,包括周期轨道,同宿轨道和异宿轨道.
这里的Bendixson判据定义如下:设x→P(x)是一个矩阵函数,且对x∈D它是C1的,假设P−1(x)存在且x∈K上是连续的,K∈D是一个紧的吸引集,定义
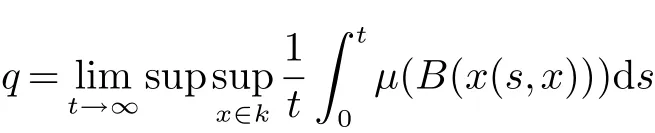
这里是把矩阵P的每一个元素Pij,用Pij沿f的方向导数取代得到的矩阵,µ(B)是矩阵Lozinshil测度
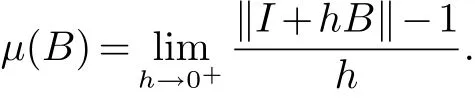
定理2[9]若D是单连通区域,且条件(H1)和(H2)成立,则当q<0时,系统x˙=f(x)的唯一平衡点x∗在D内是全局渐近稳定的.
下面应用定理2来讨论系统(1)持续带毒平衡点E∗=(x∗,y∗,v∗)的稳定性.
定理3若R0>1则E∗=(x∗,y∗,v∗)在Γ内是全局渐近稳定的.
证明由定理1可得到R0<1时,E0是全局渐近稳定的,排除了持续性的任何可能性,由文献[10]中定理4.3得到R0>1是一致待续的充分条件,当R0>1时,令x=R3且E=Γ,系统(1)满足文献[10]中定理4.3的所有条件,在边界集∂Γ上的最大不变集是点集{E0}且是孤立的,因此对系统(1)一致持续的充分条件等价于E0是不稳定的,当且仅当R0>1时,E0是不稳定的,故系统(1)在˚T内是一致持续的,因此,在D内存在一个紧吸引子集K,故定理2的假设(H1)与(H2)成立.
注系统(1)在有界集内中的一致持续性等价于系统(1)在内部中存在一个紧吸引子集K⊂Γ.
下面验证q<0.令,则p是C1且在内是非奇异的,令f表示系统(1)的向量域,则
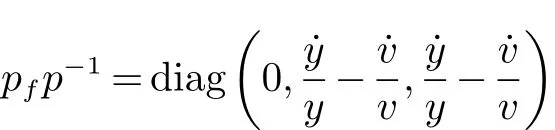
系统(1)一般解X(t)=(x(t),y(t),v(t))的第二加性复合矩阵为:
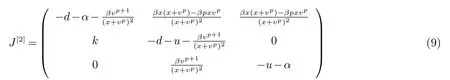
令矩阵
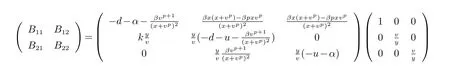
其中
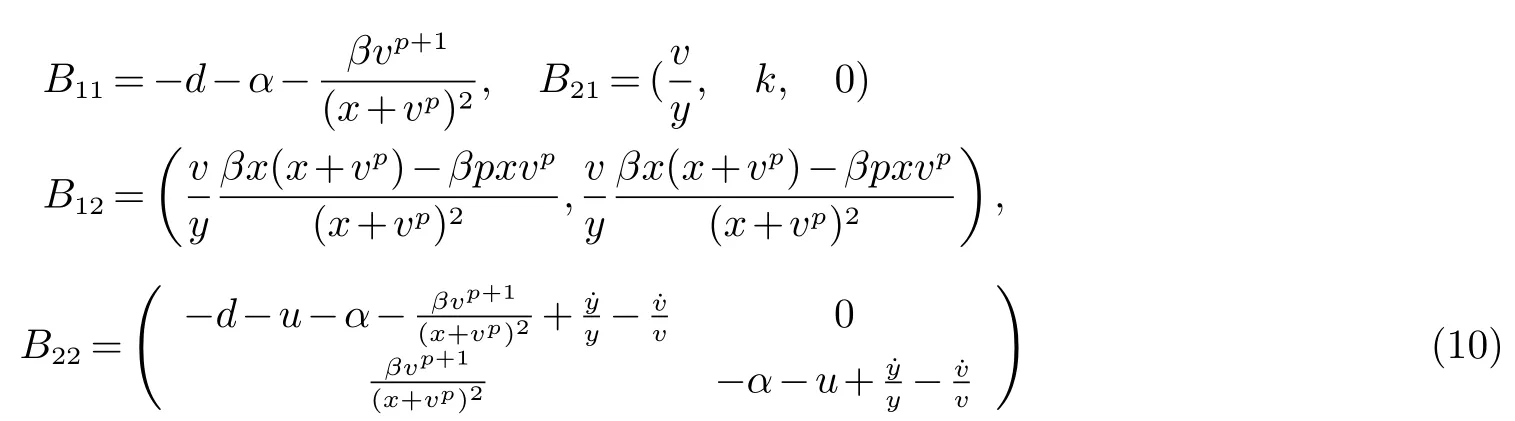
令(x,y,v)是R3中的一个向量,定义在R3中的向量模为
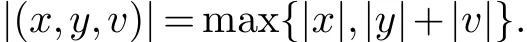
令µ为这个模的Lozinski.令
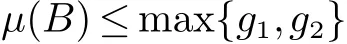
其中为L1模下的Lozinski测量值,则由上可得
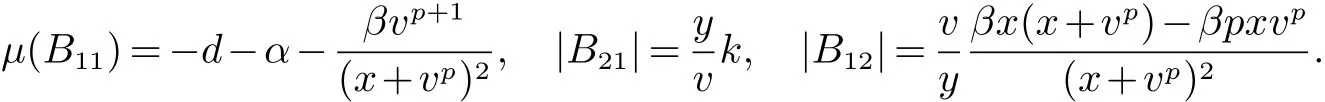
下面计算µ(B22),把B22的每一列的非对角矩阵取绝对值,然后加到相对应列的对角元素上得
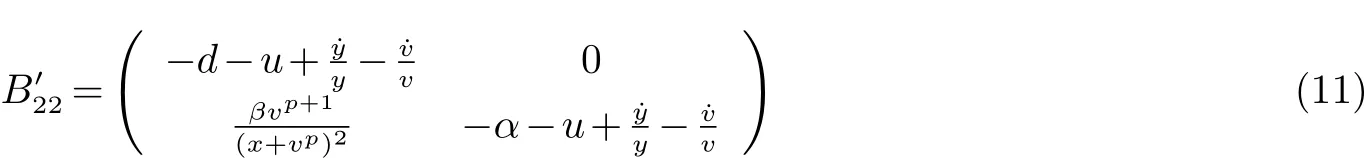
取的两个对角元素的最大值即得µ(B22),则
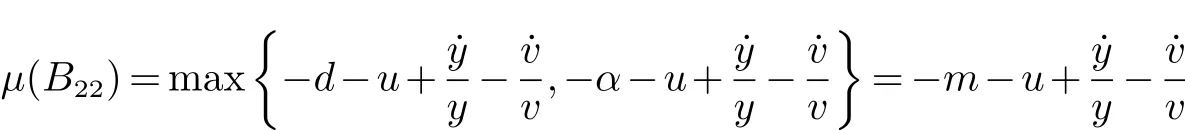
m=min{d,α}因此,当t>t∗时,
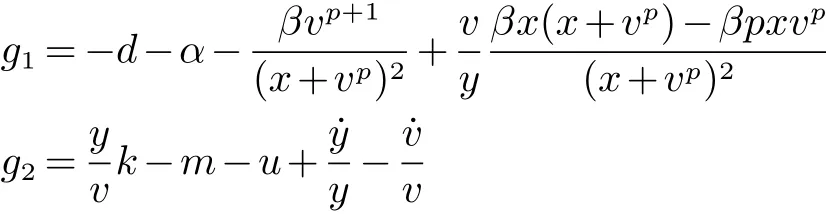
又因为

所以
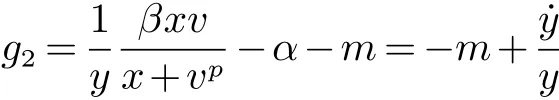
由于
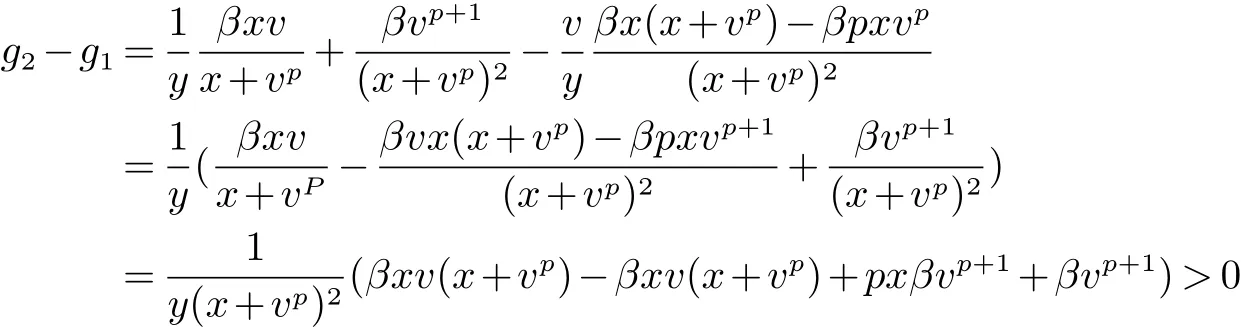
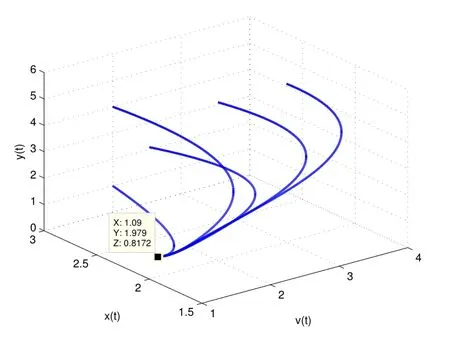
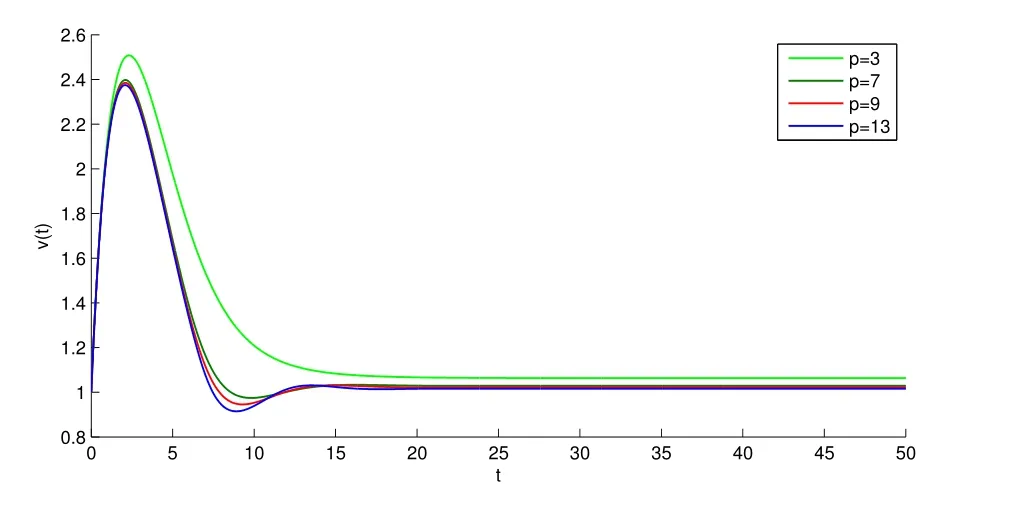
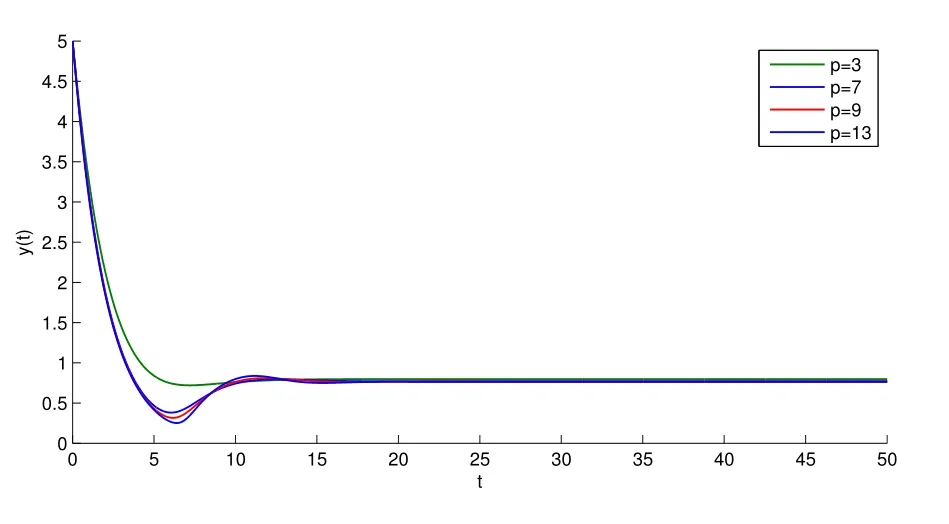
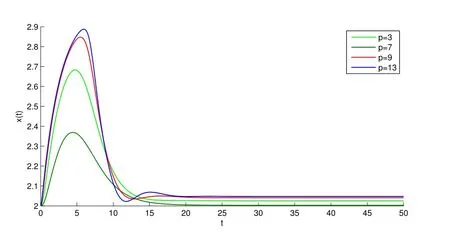
因此,g1 对t>t∗从而 又因为 从而 因此定理2的全部条件满足,故结论成立,可得到E∗是全局稳定的.即,若R0>1,则系统(1)的持续带毒平衡点E∗=(x∗,y∗,v∗)是在˚T内全局渐近稳定的. 这一部分,对系统的平衡点E∗=(x∗,y∗,v∗)在R0>1时,取不同的p值进行数值模拟,数值仿真采用Matlab软件.通过一些数值实例来说明结论的正确性和方法的有效性.如图1∼图4,这里模型中的参数分别取为λ=1.2,d=0.4,β=0.6,k=0.4,α=0.5,u=0.3,p=13,9,7,3,x(0)=2,y(0)=5,v(0)=1,此时R0=1.6>1. 这篇文章主要研究了模型(1)的动力学性质,通过建立新的Lyapunov函数并且利用微分方程中相关的稳定性理论,在基本假设(H1)和(H2)下,得到模型(1)的全局渐近稳定性.即无病平衡点是全局渐近稳定的当且仅当基本再生数R0<1,持续带毒平衡点是全局渐近稳定的当且仅当基本再生数R0>1,我们讨论的是模型发生率是当p≥2时的情形,可以看到应用的发生率比文献[8]中的更一般些,同样得到了持续带毒平衡点是全局渐近稳定的当且仅当基本再生数R0>1的结论. 图1 x(t),y(t),v(t)的立体图像 图2 v(t)与参数p的图像 图3 y(t)与参数p的图像 图4 x(t)与参数p的图像 参考文献: [1]Nowak M A,May R M.Viral dynamics[M].Oxford:Oxford University Press,2000. [2]Liu W M,Hethcote H W,Levin S A.Dynamical behavior of epidemiological models with nonlinear incidence rates[J].Math Biol,1987,25(4):359-380. [3]Vargas De Leon C.Constructions of Lyapunov Functions for Classics SIS,SIR,and SIRS Epidemic model with Variable Population Size[J].Acta Mathematica Scientia,2001,10(5):75-83. [4]Song X Y,Neumann A U.Global stability and periodia solution of the viral dynamics[J].Math Anal Appl,2007,329(1):281-297. [5]Korobenikov A.A Lyapunov fuction and global properties for SIR and SEIR epidemicological models with nonlinear incidence[J],Math Biosci Eng,2004,1:57-60. [6]Li J,Zhang J,Ma Z.Global analysis of some epidemic models with general contact rate and constant immigration[J],Appl Math Mech,2004,25(4):36-41. [7]Li G,Jin Z.Global stability of a SEIR epidemic model with infectious force in latent,and immune period[J].Chaos,solitons and Fractals 2005,25:1177-1184. [8]JI Yu,MIN Le-quan,SU Yong-mei.Global stability of a viral infection model with saturatinon incidence[J].Journal of Biomathematics,2010,25(2):267-272. [9]M Y Li,J S Muldoweny.A geometric approach to the global-stability problems[J].Math Anal,1996,27:1070-1083. [10]H R Freedman,S G Ruan and M X Tang.Uniform persistence and fl ows near a close positively invariant set[J].Dyn DiffEqus,1994,6(4):583-600.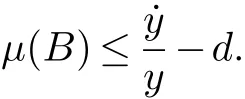
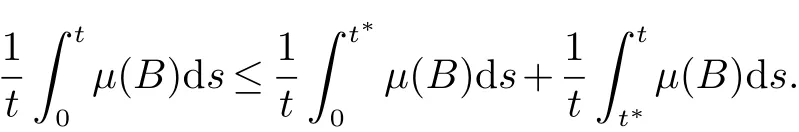
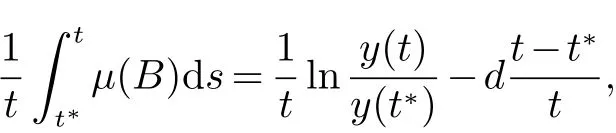
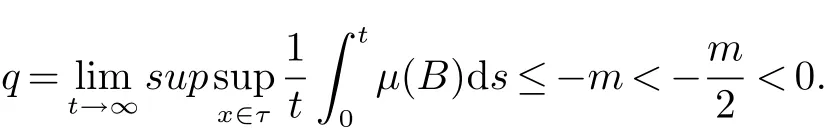
4 数值模拟
5 讨论