基于ANSYS的曲柄摇杆机构的优化设计∗
刘小月,木合塔尔克力木,巨刚
(新疆大学机械工程学院,新疆乌鲁木齐830047)
0 前言
在机械设计与制造领域里,曲柄摇杆机构是能实现某种复杂运动轨迹的机械机构.在现实生产中往往是根据给定运动的轨迹来设计制造所需机构,而设计中是依据给定轨迹上的有限个点来设计曲柄摇杆机构,往往设计完成的曲柄摇杆机构不能和目标轨迹相符合,这就引起了对设计好曲柄摇杆机构参数进行优化设计的问题[1].
曲柄摇杆机构是铰链四杆机构基本形式之一[2],由于其具有运动副接触面积大、润滑方便、磨损较轻、运转可靠等诸多优点而在工程实际中得到了广泛应用.设计四杆机构的时候,往往会出现多参数设计情况,很显然这种情况属于多目标优化设计问题[3],设计人员往往会采用优化设计方法来解决这一问题.
在机构优化设计中,总是希望设计出体积小、重量轻、承载能力大、传动效能好的传动机构.如今优化设计方法很多,在铰链四杆机构的优化设计中,很重要的一步就是确定优化设计的数学模型和确定优化设计方法[4].本文研究的是在给定目标位置点的情况下,对曲柄摇杆机构的参数进行优化设计,根据优化曲柄摇杆机构简化模型,建立优化数学模型,并用ANSYS软件进行设计分析,得出曲柄摇杆机构最优化参数,确定最优化设计结果.
1 建立曲柄摇杆机构模型
1.1 确定目标函数
如图1所示,设计曲柄摇杆机构,使得连杆BC上的点M的轨迹尽量地接近给定的目标位置点(xi,yi),其中(i=1,2...,n).

图1 曲柄摇杆机构模型
设点M的轨迹为(xMi,yMi)(i=1,2...,n),为使得轨迹点尽量接近目标位置点,应使所有轨迹点和目标点位置之和最小[5].令
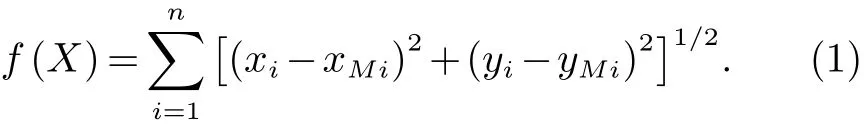
为了简化计算,取目标函数为
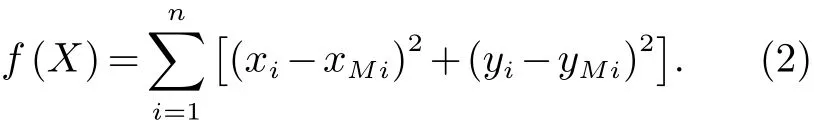
取设计变量为:X=[a,b,c,d,k,xA,yA,β,γ]T,由于a,b,c,d,k为各杆长度,均大于零.
1.2 确定约束条件
1.2.1 存在曲柄约束条件
AB为曲柄且为最短杆,所以各杆长度应满足约束条件
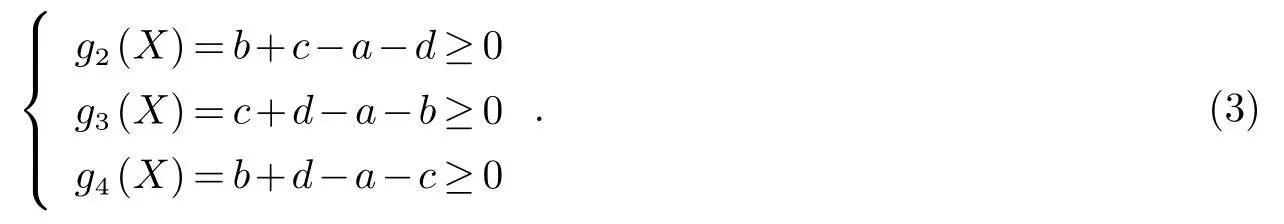
1.2.2 存在最小传动角约束条件
为了使曲柄摇杆机构能满足正常工作条件,取其最小传动角不小于30o,各杆满足性能约束条件
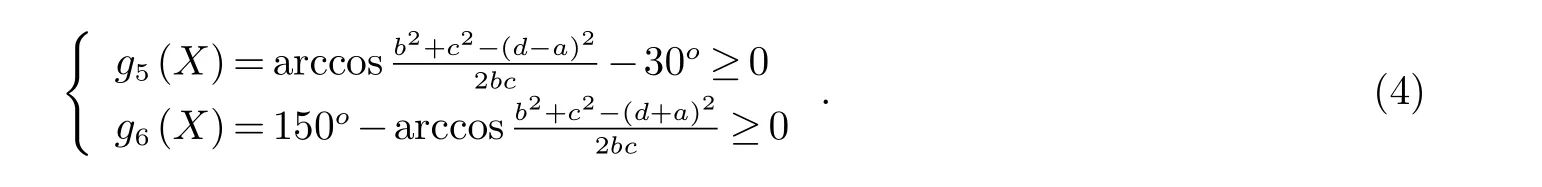
1.2.3 边界约束条件

1.3 建立优化数学模型
优化设计目标是确定问题的最优解X∗,使得

将目标函数和约束条件整理即可得到本问题的优化数学模型
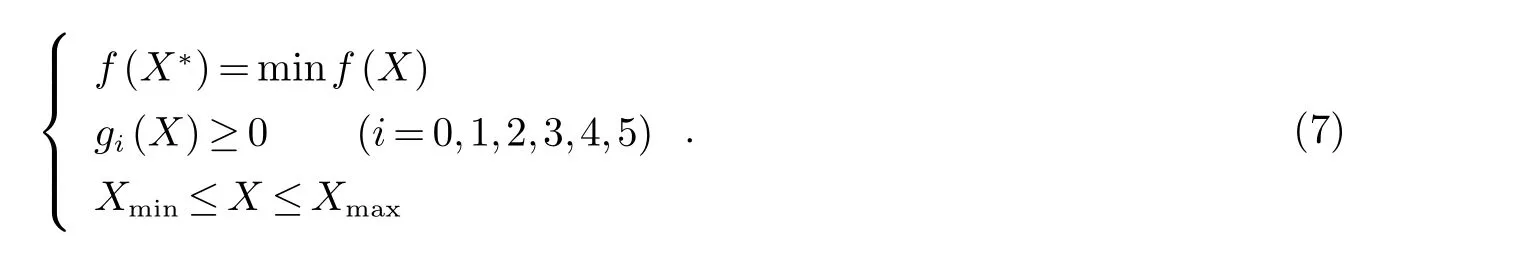
2 ANSYS优化设计方法理论
优化设计是ANSYS的高级分析技术,直接使用ANSYS分析的各种结果,不需要为目标函数、约束条件建立解析方程.
2.1 ANSYS优化方法及工具
ANSYS的优化设计模块提供两种优化设计方法,一阶分析法(First-order)和最优梯度法(Gradient),即目标函数和状态变量对设计变量的一阶微分.
优化工具是搜索和处理设计空间的技术,也可以作为优化方法使用,ANSYS提供单步法(single run)、随机搜索法(Random Design)、乘子评估法(DV Sweep)及子问题计算法(Sub-problem)等.
2.2 ANSYS优化约束条件
假设Fj−1、Xj−1和Fj、Xj为目标变量和设计变量的第j次和第j−1次迭代结果.F0、X0为目前最优的目标变量值和相应的设计变量值,那么满足以下式子任意一个条件时认为迭代收敛,于是迭代停止.
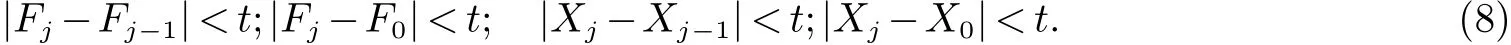
其中t为设计目标变量或设计变量允差.
2.3 ANSYS优化设计流程算法
采用ANSYA软件与优化导重准则法集成的方式,与ANSYS的集成有两种方式:一是在ANSYS中直接调用数据来获取文件,自动完成结构的优化设计计算,此方法可以避免人为因素对优化效率的影响;二是在结构优化中直接调用ANSYS的核心程序对优化问题进行参数化建模和结构分析.这里采用第一种方式.ANSYS优化设计框图如图2所示.

图2 ANSYS优化设计框图
(1)在ANSYS中建立结构的参数化分析模型,作为设计变量的参数必须保证其在取值范围内可以变化,在ANSYS优化分析中,至多可以定义60个设计变量的参数;
(2)对原始结构或新的设计点进行有限元分析;
(3)进行收敛判断,如果满足收敛条件,则输出当前的设计,结束计算,若不满足转下一步;
(4)在敏度分析命令流文件中设置设计变量、状态变量和目标函数,利用ANSYS的梯度法求解目标函数和状态变量对设计变量的敏度;
(5)进行优化计算,求解新的设计点,返回步骤(3).
3 工程实例分析
图3是用ANSYS软件建立的发动机活塞机构三维模型.笔者以发动机活塞机构为实例,采用ANSYS软件优化曲柄摇杆机构参数,使M点得出最优轨迹.
3.1 初始值及初始条件
(9.50,8.26),(9.00,8.87),(7.97,9.51),(5.65,9.94),(4.36,9.70),(3.24,9.00),(3.26,8.36),(4.79,8.11),(6.58,8.00,),(9.12,7.89)
给变量赋初值:
a=2,b=8,c=7.5,d=9.5,k=7,yA=4,yA=4,γ=.根据实际条件,各杆长度值介于(0.1∼10)之间,各角度值介于(0.1∼π)之间.
利用上述数学模型,采用ANSYS进行分析计算,得到优化结果数值,如表1所示.

表1 ANSYS分析下优化参数
4 优化结果处理
图4是在ANSYS分析下生成的优化方案列表;图5是M点给定的十组目标点的曲线;图6是M点给定目标曲线和三组用ANSYS优化的轨迹曲线,明显可以看出,第一、二、三组曲线和目标曲线很接近.其中第三组曲线相比第一、二组曲线更逼近目标曲线;图7是最佳优化曲线,其参数值为:
a=2.213 3,b=7.732 8,c=7.806 6,d=9.423 1,xA=1.071 7,yA=4.027 2,β=0.389 18+π/2,k=7.732 8,γ=1.006 3.
处理结果证明第三组数据参数是最优参数,本方案也是最优方案.对曲柄摇杆机构来说,用ANSYS的这种分析方法具有实际借鉴意义.
5 结论
笔者采用ANSYS法,以曲柄摇杆机构优化模型为依据,建立目标函数及几种约束条件,对目标位置点进行优化设计.以发动机活塞机构为工程实例在ANSYS中建立优化分析文件和优化控制文件,对曲柄摇杆机构参数进行优化分析,得出优化分析数据.用图形比较的方式得出最佳数据方案,并证实了用ANSYS分析的方法在优化曲柄摇杆机构时,具有实际借鉴意义.
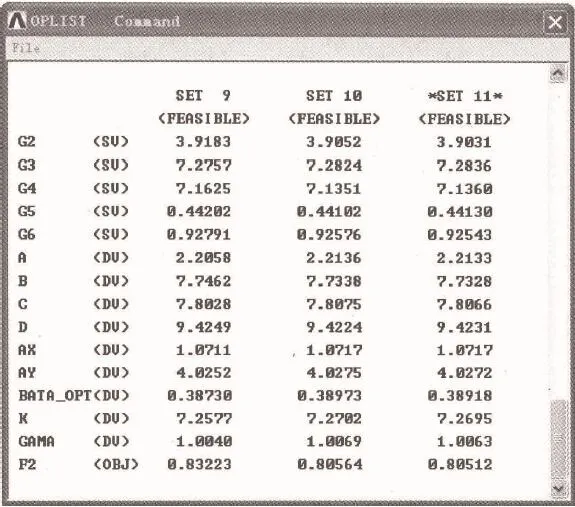
图4 ANSYS生成方案列表
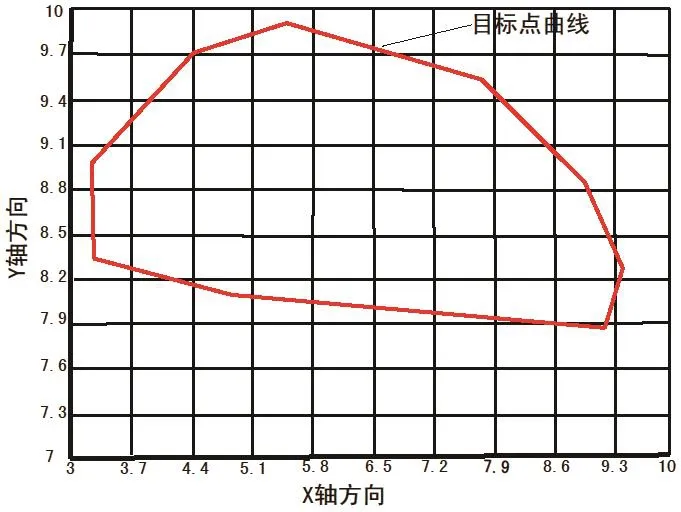
图5 目标曲线
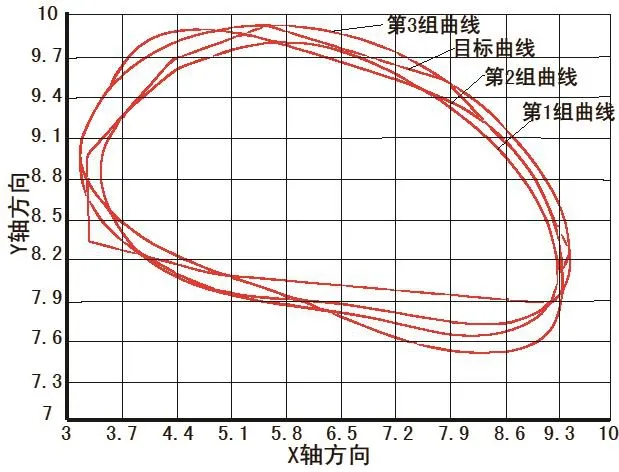
图6 目标曲线和优化曲线对比
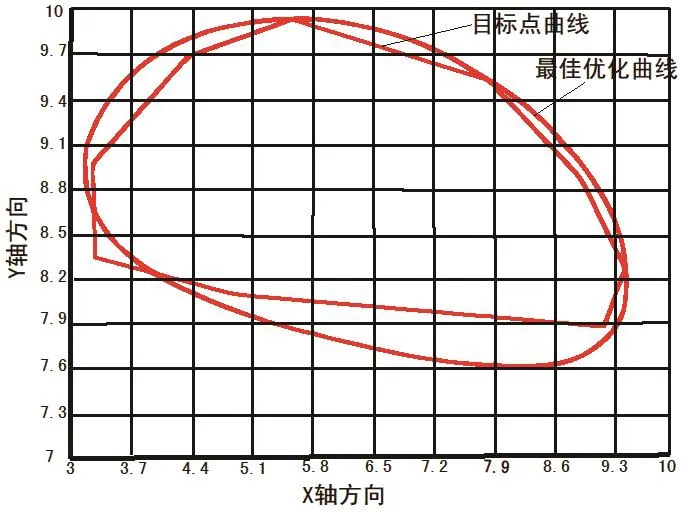
图7 最佳优化曲线
参考文献:
[1]程友联,吴晓红.曲柄摇杆机构的参数设计法[J].机械设计,2010,27(9):61-96.
[2]苏有良.按最小传动角最大的曲柄摇杆机构优化设计[J].机械设计,2014,31(6):30-33.
[3]董二宝,李永新.单曲柄双摇杆机构同步性能优化[J].机械工程学报,2010,46(7):23-26.
[4]陈应舒.基于DFM的曲柄摇杆机构的优化设计[J].机械设计与制造,2012,(10):36-37.
[5]周廷美,蓝悦明.机械零件与系统优化设计建模及应用[M].北京:化学工业出版社,2004.
- 新疆大学学报(自然科学版)(中英文)的其它文章
- WSNs中基于Chebyshev多项式的可认证密钥协商方案∗
- 新疆双峰驼乳清蛋白组分对人宫颈癌HeLa细胞增殖的抑制作用∗
- 新疆加曼特金矿与斑岩型金矿的对比研究∗
- 具有非倍测度的参数型Marcinkiewicz积分交换子在Hardy空间的估计∗
- Periodic Solution of a Two-species Competitive Model with State-Dependent Impulsive Replenish the Endangered Species∗
- Permanence and Extinction for Nonautonomous SIRS Epidemic Model with Density Dependence∗

