小振幅波在连续密度分层液膜中的研究∗

樊小朝，王维庆，史瑞静，于晓燕，黎进，买代，黄宝阳，李坤康

(1.新疆大学电气工程学院，新疆乌鲁木齐830047；2.教育部可再生能源发电与并网控制工程技术研究中心，新疆乌鲁木齐830047)

0 引言

当流体微团受到扰动离开原来平衡位置时，重力、表面张力或其它回复力就要发挥作用，使流体回到平衡位置，运动不会中止，回复力再次作用，因此波动形成[1−3].按波动振幅的大小分为小振幅波、有限振幅波、大振幅波[4−6].所谓分层流体，是指密度或熵非均匀的流体[7−9].自然界中流体(如大气、海洋、湖泊及液膜等)，由于其密度、盐度或温度变化，均认为分层流体[10−12].分层流体分类：间断分层(也称强分层）流体、连续分层流体以及由连续分层和均匀分层组合而成的分层流体[13,14]，如图1所示.

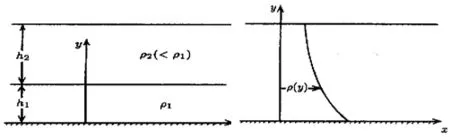
图1 间断及连续分层流体

关于波动在分层液膜的研究，D.Merkt[15]利用长波近似理论，在分层液膜内部有自由表面的条件下，得到了时域演化方程；Tilley与Davis[16]提出了强分层流体沿斜板流动的稳定性理论，并研究了长波内部扰动对液膜的影响；Andrey Pototsky[17]研究了强分层液膜在绝热壁面上流动稳定性.对连续密度分层液膜中波动的研究很少见，因此，本文将对连续密度分层液膜中的小振幅波进行理论研究，揭示液膜的流动稳定性机理.

1 数学物理模型

二维小扰动的物理模型如图2所示.

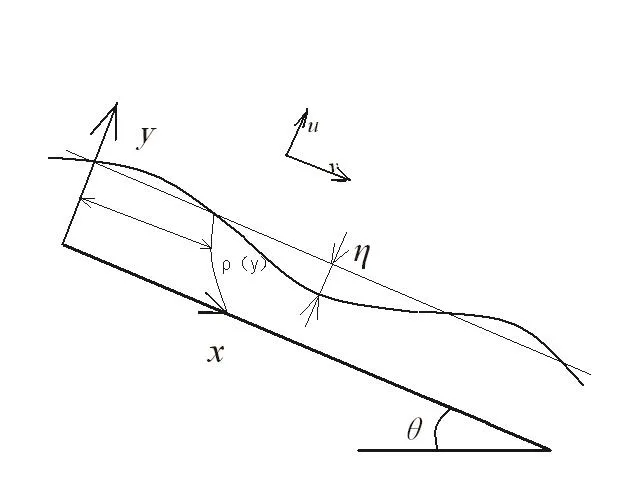
图2 连续密度分层液膜中小振幅波

设u、v为x、y方向的速度分量，密度、压强为ρ、p，µ为动力粘性系数，带有粘性项的二维方程为

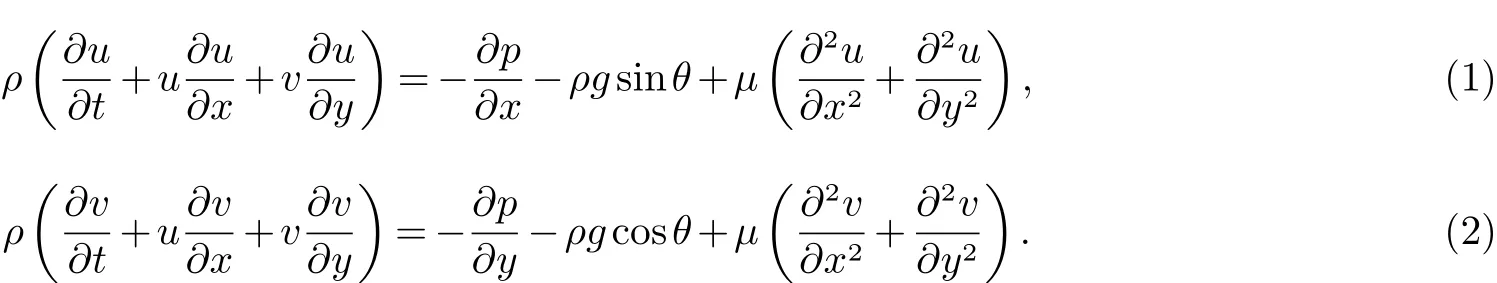
设液膜平均厚度为d，x方向主流速度：u0=ρgd2sinθ/2µ，带*表示无量纲量，则

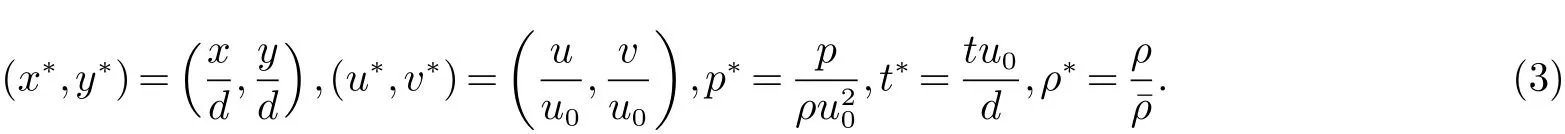
由小扰动理论，令

其中“—”为平均值，“p0,ρ0”为扰动压强、扰动密度.

密度分布静压分布¯p满足，代入运动方程，由线性理论[8,9]，忽略扰动量的高阶项，得无量纲方程（去掉*）

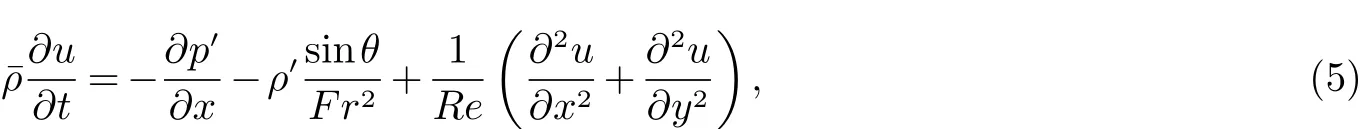
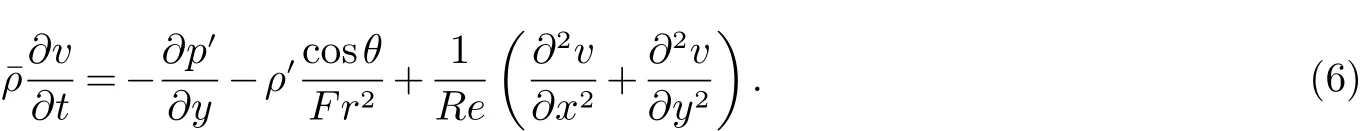
其中雷诺数Re=u0d/v，弗罗德数

引入流函数

其中，k是波数，c是波速，速度分量可表示为

由无量纲方程消去p0，再将ρ0及u、v代入，得

其中振动频率σ=kc.

底面y=0无滑移边界条件为

在自由面上压强

设η为自由表面波动位移，自由表面边界条件为

在y方向上，速度v=∂η/∂t，则

由式子（5）和（8），并忽略粘性项和重力项，有

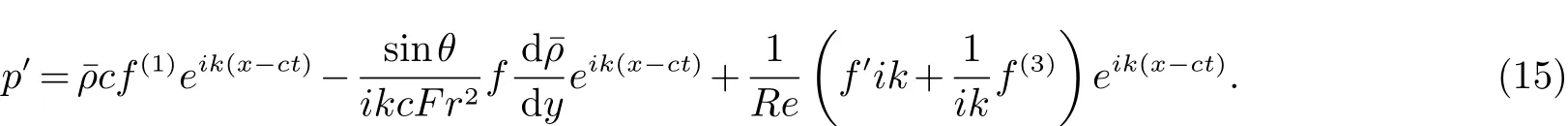
将（14）、（15）代入（13），得自由表面的边界条件为

联立方程（11）、（16），构成特征值求解问题.分析得到，若k、及d已知，可确定c2；若c2或σ2给定，k2可确定.

2 特征值方程参数讨论

2.1 斯特姆-刘维尔（Sturm-Liouville）理论

两个Sturm-Liouville[3]问题：

问题一：

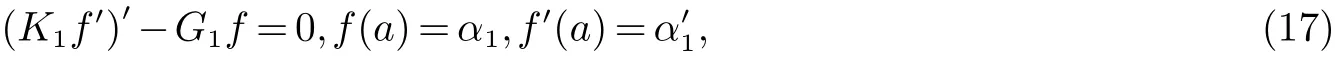
问题二：

为了使上述问题有解，令

系数Ki，Gi满足

并且α16=0，α26=0以及

Sturm-Liouville问题的两个比较定理成立.

比较定理Ⅰ：问题一、二的零点为z1i(6=a),z2i(6=a)，则必有

比较定理Ⅱ：若f1(b)6=0,f2(b)6=0，则必有

2.2 特征数分析

1）小振幅波特性分析

假设随着波数k的增大波速c增大.应用斯特姆-刘维尔理论，由于K1=K2=¯ρ，则

注意到<0，所以G相应地也增大，由比较定理Ⅰ，零点满足关系（22），

因此两个本征函数必有一个不满足边界条件f(d)=0.

对于自由面的情况，由比较定理Ⅱ，得

即c1n>c2n，这同原先假设的c随k增大相矛盾.

因此，得到结论：c随k增大而减小.

2）波频率与波数的关系

将方程除以k2后得到

假设k增大时σ减小，由比较定理Ⅱ，则

又σ=kc，则

这与原假设相矛盾，因此σ随k的增大而增大.

3）内波的最大频率

由(11)知，f(y)是解，−f(y)也是解，设f0(0)>0.因f(0)=0，所以在y=0的邻域内有f(y)>0.若

由（11）式可知，，则在y=0邻域内从而f0>0，因此f(y)不断增加.式（24）右端为频率，为分层液膜中内波的最大频率.

4）波速的本征值

密度连续时，频率σ有界，即

在密度连续分布的有界区域内，其波速也是有界的.取

构造方程

当两端固定时，其本征值为

在方程(11)中，k下降时，c将增大，当k=0时，c值最大，即

应用Sturm-Liouville比较定理，有

本征值c可无限接近于原点，分布在区间[0,c1]上，并以原点为它的聚点，如图3所示.

图3 波速本征值分布示意图

3 结论

建立了密度分层液膜的小振幅波数学物理模型，对模型进行了无量纲化及小振幅线性简化，得到了描述小振幅内波的控制方程及其边界条件.利用Sturm-Liouville比较定理，研究了描述液膜的波动特性的波动参数（波数、波动频率、波速）及其相互关系，得到如下结论：

(1)无论上表面是自由表面还是固定壁面，波速c都随波数k增大而减小，波动频率σ随波数k的增大而增大；

(2)密度分层液膜中的小振幅内波存在一个最大频率，即频率；

(3)密度分层液膜中的小振幅内波存在最大波速值

(4)波速c的本征值分布在区间[0,cmax]上，并以原点为聚点.

参考文献：

[1]梅强中.水波动力学[M].北京:科学出版社,1984.

[2]Chen L,Zhang D,Chen W.Numerical simulation and test on two-phase fl ow inside shell of transfer case based on fl uidstructure interaction[J].Transactions of the Chinese Society of Agricultural Engineering,2014,30(4):54-61.

[3]叶学民,姜凯,沈雷,等.含活性剂超薄液膜演化过程的稳定性研究[J].力学学报,2013,45(5):681-689.

[4]李家春.分层流中的瞬变波[J].力学学报,1983,11(6):611-622.

[5]陈胖胖,常瑞,王军.分层计算冰盖弹模对冰盖破裂的影响分析[J].水力发电学报,2013,32(3):134-138.

[6]邵莉,刘利民,苑伟,等.R134a卧式螺旋管内沸腾两相流型与传热特性实验研究[J].原子能科学技术,2013,47(3):391-396.

[7]周光垌.流体力学[M].北京:高等教育出版社,2001.

[8]戴世强.两层流体界面上的孤立波[J].应用数学和力学,1982,6(3):721-731.

[9]易家训.分层流[M].北京:科学出版社,1983.

[10]王才欢,段文刚,聂艳华,等.水电站进水口分层取水水力特性模型试验研究[J].水力发电学报,2013,32(5):122-128.

[11]Wang R,He Y,Qiao J.Study on the Generational Mechanism of Bidirectional Sedimentary Structure by Internal-Waves[J].Advances in Geosciences,2013,3(2):568-597.

[12]谢锴,郭晓镭,丛星亮,等.工业级水平管粉煤气力输送的最小压降速度和稳定性[J].化工学报,2013,64(6):1969-1975.

[13]SUN W Q,ZHANG J L,ZHENG Q C,et al.Molecular Dynamics Simulations of the Unbinding of Phenyl sulfonamide from Carbonic Anhydrase II[J].Acta Physico-Chimica Sinica,2013,29(4):843-848.

[14]张雪东,公茂琼,吴剑峰.替代工质水平管内流动凝结换热研究综述[J].制冷学报,2013,34(5):28-33.

[15]Merkt D,Pototsky A,Bestehorn M,et al.Long-wave theory of bounded two-layer films with a free liquid–liquid interface:short-and long-time evolution[J].Physics of Fluids(1994-present),2005,17(6):064104.

[16]Tilley B S,Davis S H,Banko ffS G.Linear stability theory of two-layer fl uid fl ow in an inclined channel[J].Physics of Fluids(1994-present),1994,6(12):3906-3922.

[17]Pototsky A,Bestehorn M,Merkt D,et al.Morphology changes in the evolution of liquid two-layer films[J].The Journal of chemical physics,2005,122(22):224711.