展向周期变化槽道流中全局稳定性的数值模拟
孔 玮,罗纪生
(天津大学机械工程学院,天津 300072)
展向周期变化槽道流中全局稳定性的数值模拟
孔 玮,罗纪生
(天津大学机械工程学院,天津 300072)
用数值模拟的方法研究了基本流在展向周期变化的槽道流的全局稳定性问题.首先用线性稳定性理论求得的扰动特征函数作为初始值,计算扰动随时间的演化.经过充分的发展后,得到了全局稳定性的特征解.给出了不同展向变化幅值下的计算结果和全局稳定性下的中性曲线,分析了全局中性时雷诺数与展向不均匀程度的关系以及特征函数的性质.
全局稳定性;展向周期变化;槽道流;数值模拟
在大多数情况下,流动稳定性理论中研究讨论的是基本流只与一个坐标有关的流动,如槽道流中,基本流只是壁面法向坐标的函数.但一般来讲,基本流可能还与其他的坐标有关,这类流场的稳定性分析就比较复杂了.因此,在流动稳定性分析中,扰动的稳定性问题通常用局部分析(local analysis)和全局分析(global analysis)两种方法来研究.
局部的分析方法研究的是基本流只与一个坐标有关或基于平行流假设下近似的只与一个坐标有关的情况,即针对的是平行剪切流,通过求解 Orr-Sommerfeld方程(简称O-S方程)的特征值问题来进行分析;而对于基本流是多个变量的函数,如果采用局部分析的方法,需要假定流场随法向坐标以外的其他变量是缓变的,从而转化成参数形式的 O-S方程进行求解,这样在不同的参数下特征值都会不同,往往无法对整体稳定性进行准确预测,所以通常需要采用全局的分析方法,按照全局理论,流场应该在整体上具有一致的增长衰减性,即得到的是全局特征解.
全局稳定性理论研究起始于 Huerre和Monkewitz[1]在 1990年的工作,2005年 Chomaz[2]对此问题进行了回顾,在此期间也有许多研究工作有过一定程度上的进展[3-8].虽然流动稳定性的全局分析与局部分析从概念上讲是类似的,但局部分析研究的是常微分方程的特征值问题,而全局分析研究的是偏微分方程的特征值问题.因此,全局分析的计算量是巨大的,通过 QZ方法[9]直接求解这么大的特征值问题,计算效率非常低,有时甚至是不可能的.虽然可以用一些其他的方法进行求解,但对计算技巧及计算量的要求都比较高.
由于通常研究的槽道流只和壁面法向坐标有关,是一种典型的平行流,因此对于这种流动的稳定性可以由局部线性稳定性理论[10]进行分析,并且早已有过研究且已经成熟.但在工程或真实情况下流动是不可能完全平行的或只随一个坐标变化,比如Stokes层就是一种随时间变化的流动,而研究此类流动更显得具有实际意义.对于本文研究的展向周期变化的槽道流,则需要求解全局特征值问题,但是其计算量非常大.本文则通过数值模拟的方法研究了这种流动的全局稳定性问题.
1 基本流、控制方程与数值方法
1.1 基本流
本文研究的是基本流展向周期变化的槽道流,即流动除了流向的压力梯度外,还由展向周期变化的体积力引起.
槽道流的坐标如图 1所示.其中 x、y、z分别为流向、法向和展向,h为半槽道宽,Um为最大基本流速度.
用 Um作为特征速度,半槽宽h作为特征长度,密度ρ作为特征速度,h /Um作为特征时间尺度,作为特征压力尺度,对流体力学的不可压缩原始Navier-Stokes方程进行无量纲化.无量纲化后的Navier-Stokes方程对应的层流方程为

式中:ui是速度;是坐标(x,y,z);p是压力;Re = Umh/ν是雷诺数;fxi是体积力项.
设 U1、U2、U3分别为流向、法向和展向的基本流速度.考虑在流向加入沿展向周期性变化的体积力及流向的压力梯度,可将式(1)化简为
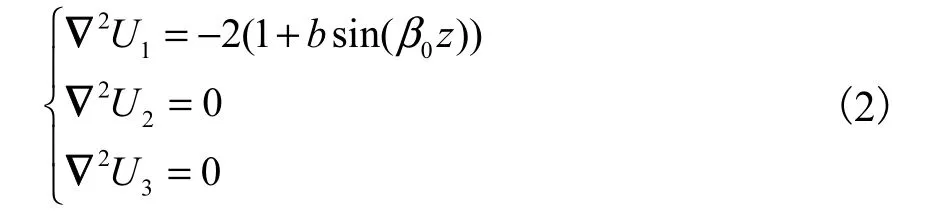
式中:b是基本流展向变化部分的的幅值;β0为展向基本波数.

当b=0时,基本流为通常槽道流的速度剖面;当b≠0时,为展向周期变化的槽道流.图 2给出了b=0.2时基本流在 yz平面上的等值线图,可以看出,基本流速度 U1在展向是周期性变化的,图中给出了沿展向2个周期的结果.

图2 b=0.2时基本流速度 U1在yz平面的等值线图Fig.2 Contours of base flow U1in the yz plane when b=0.2
1.2 控制方程
将基本流写成只含有 y的部分和含有展向变化的部分,即
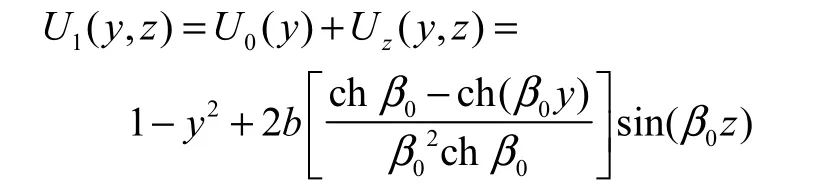
把与 Uz相关的项写到方程右边,得到数值求解的扰动方程(为求简洁,略去扰动量的上标)为

其中

1.3 数值方法
本文在流向和展向采取傅里叶谱方法进行计算,其中展向网格数依据计算具体情况而定;在法向使用Chebyshev配置点法,网格数为 129,时间上采取二阶精度的显隐差分格式[11]进行计算,时间步长依据计算所取不同展向网格数而定.
将式(4)中的各函数在流向和展向展开为Fourier级数的形式,再在谱空间求解.

式中 ωr是由 O-S方程求解出的特征值实部;α 为流向波数.流向和展向计算域长度分别是
式(4)变为
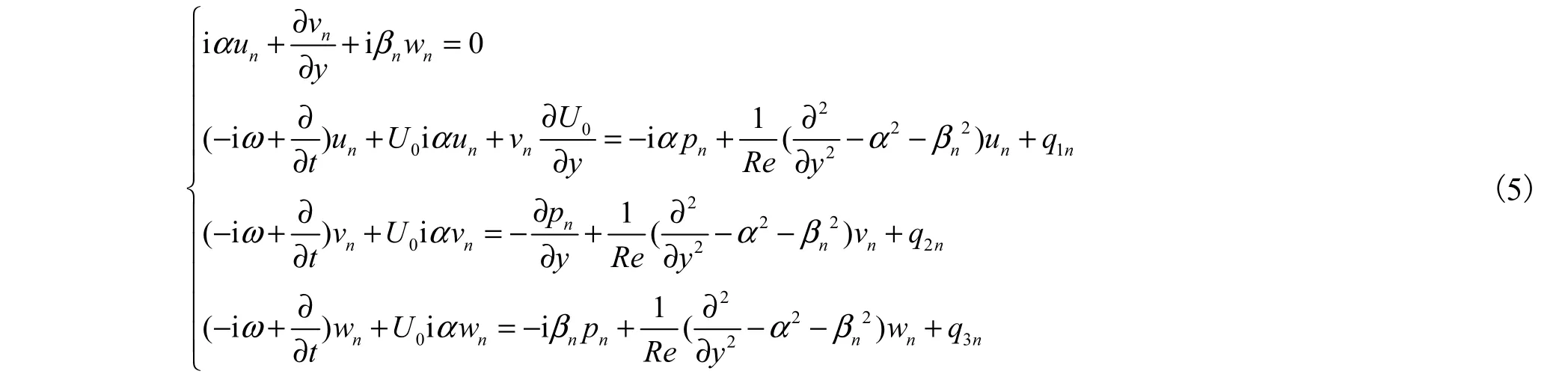
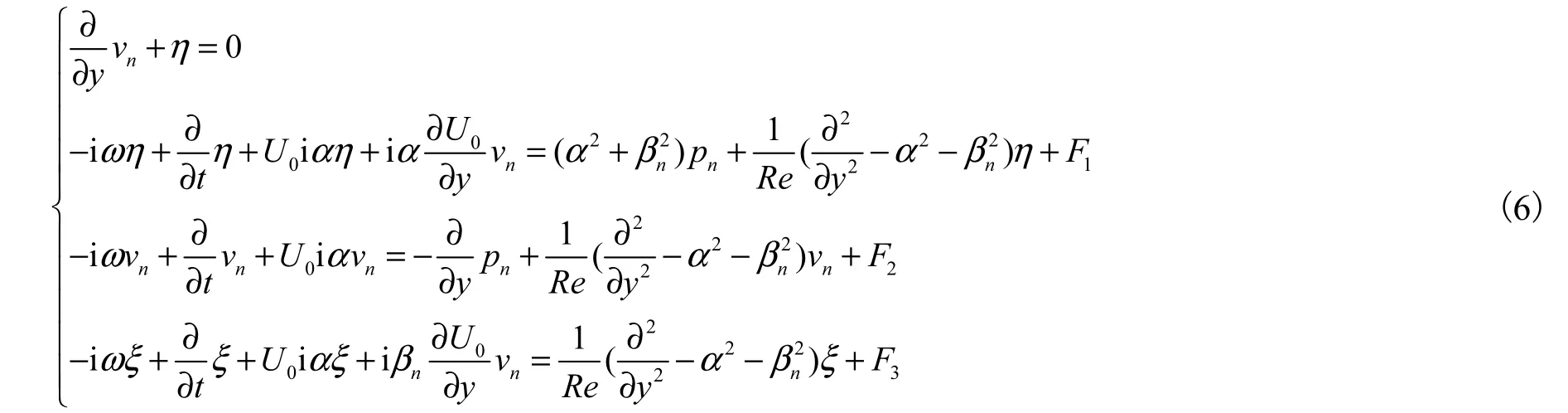
其中

将方程(6)写成算子的形式,即
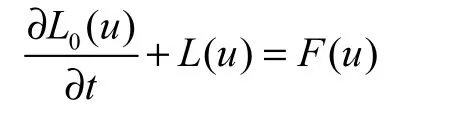
式中:L(u)是与 Uz无关的项,采用时间隐格式求解;为与 Uz相关的项,采用显格式进行求解.于是在时间方向离散后的算子形式可写成

时间方向离散后,式(6)可写成

其中
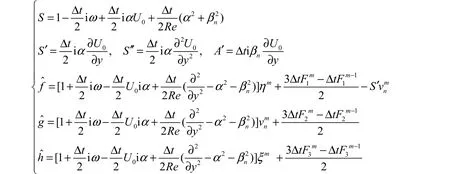
联立方程组(7)可解得η、vn、pn,求出 vn后,再代入式(7)中第 4式求出ξ,再由出了0~8阶谱的结果).从图中可以看出,扰动在经过前期的调整后,随时间是呈现指数增长的,并且从求得

2 计算结果及分析

图4 扰动速度 u各阶展向谱沿法向最大幅值随时间的演化Fig.4 Variation of maximum amplitude of disturbance velocity u with time
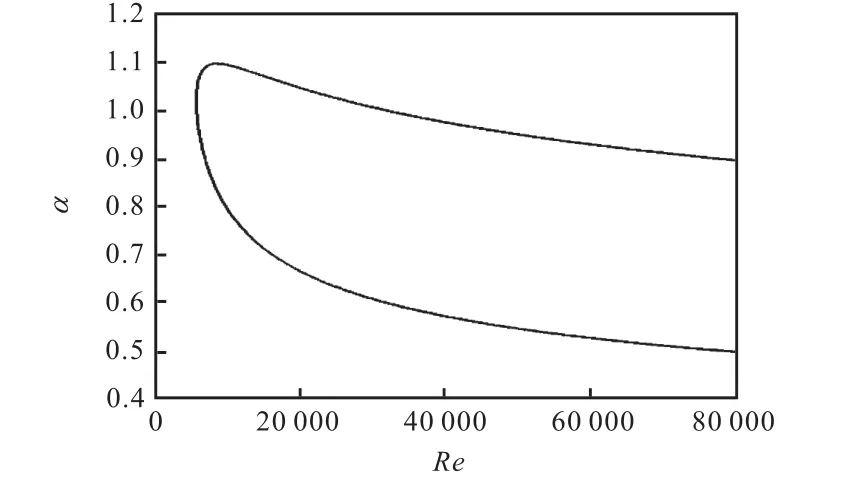
图3 一般槽道流的中性曲线Fig.3 Neutral curve of common channel flow
2.1 展向不均匀性对稳定性的影响
为了了解展向幅值 b对稳定性的影响,下面以α=1.02、Re=8,000的情况为例来进行说明.
图4是b=0.2时扰动速度u各阶展向谱沿法向最大幅值随时间的演化及其在计算前期的演化及扰动速度u的幅值取自然对数后随时间的演化(其中给取对数后各阶谱扰动速度幅值随时间的变化曲线可以看出,各阶谱互相平行,这证明它们的增长率是相同的,即各阶谱扰动的特征函数都具有一致的增长率.同时为了验证特征函数的形状是否不发生改变,用 0阶谱沿法向的最大幅值为标准对各阶谱进行归一化,得到不同时刻扰动速度u各阶展向谱的特征函数的比较,见图5(其中给出了0~5阶谱的结果).从图5中可以看到,归一化后的各阶谱扰动特征函数的形状不随时间发生改变,与t=500的结果重合,说明得到了定常解.其他两个速度分量 v和 w的情况类似,在此不再给出.由此表明,扰动在整体上具有一致的增长,得到了扰动全局增长的特征解.

图5 不同时刻以0阶谱归一化后的扰动速度u各阶展向谱特征函数Fig.5 Eigenfuctions of disturbance velocity u normalized with Fourier mode n=0 at different time

图6 展向谱n=0时扰动速度u及其增长率随时间的演化Fig.6 Variation of maximum amplitude and growth rate of disturbance velocity u(n=0) with time
下面讨论展向幅值 b对全局稳定性的影响.图6(a)给出的是 b分别为 0.2、0.324,95、0.4时扰动速度 u的 0阶展向谱幅值随时间的演化.从图中可以看出,随着b的增大,扰动是逐渐趋向于衰减的,即b对扰动起着稳定的作用.图 6(b)给出了扰动的增长率随时间的变化,即先将扰动幅值对时间求导数,然后再除以其本身,得到了增长率的大小.从图中可以看到,b=0.2时扰动的增长率大概是 0.001,3左右,而当 b=0.4时增长率为-0.000,92,变为负值,而当b=0.324,95时增长率大约为 0,即对应全局的中性解. 由此可知,在同一雷诺数下,随着b的增大,扰动波的增长率是逐渐减小直至变为衰减,一般总可以找到一个使得增长率基本为0即全局中性下的b值,统一称其为b0.
通过计算,在不同的雷诺数下找到了相应的 b0,图7给出的是在不同α下Re与b0的关系曲线.从图中可以看出,当雷诺数处于一般槽道流中性曲线下分支附近时,b0随着雷诺数的增大而增大;而当雷诺数处于中性曲线上分支附近时,b0是随着雷诺数的增大而减小的,并且随着α的增大,曲线的范围是逐渐缩小的.

图7 b0随Re的变化曲线Fig.7 Variation of b0with Re
2.2 全局中性情况下计算结果分析
以下分别给出了扰动既不增长也不衰减即中性的情况下,一些物理量的计算结果及其分析.
2.2.1 扰动速度u各阶谱沿法向的分布
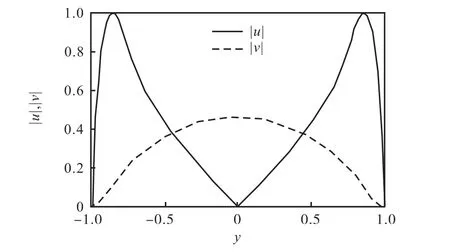
图8 归一化后扰动速度的特征分布Fig.8 Eigenfunctions of disturbance velocity u normalized with Fourier mode n=0
首先,图 8给出了α=1.02、b=0、Re=5,772.3时扰动速度的特征分布,这是通常槽道流中性曲线临界雷诺数对应的速度特征函数的结果.

图9 扰动速度 u各阶展向谱的归一化特征分布(Re=5,800,8,000)Fig.9 Eigenfunctions of disturbance velocity u normalized with Fourier mode n=0(Re=5,800,8,000)
图9和图10分别给出的是α=1.02时中性曲线下支界和上支界附近的不同雷诺数在对应 b0下扰动速度u展向谱归一化后特征分布的比较结果,其中下支界附近给出的雷诺数分别为 5,800和 8,000,上支界附近给出的雷诺数分别为 22,000和 26,000,给出了展向谱 n=1~4的结果.从比较结果上看,在中性情况下不同雷诺数下各阶谐波沿法向的分布基本是类似的.其他两个扰动速度分量 v和 w也具有相同的性质.

图10 扰动速度u的各阶展向谱的归一化特征分布(Re=22,000,26,000)Fig.10 Eigenfunctions of disturbance velocity u normalized with Fourier mode n=0(Re=22,000,26,000)
2.2.2 扰动速度u在xz平面上的等值线图
为了比较不同雷诺数下扰动在 xz平面的分布,将谱空间的扰动变换到物理空间中,并在扰动沿法向最大值处给出 xz平面上 u的等值线图.图 11和图12分别给出的是α=1.02时,中性曲线下分支和上分支附近雷诺数的计算结果.由图中可以看出,扰动在展向呈现明显的周期性变化,在中性曲线下分支附近,当雷诺数增大时,展向的不均匀性增强;在中性曲线上分支附近,当雷诺数减小时,展向的不均匀性增强.

图11 扰动速度 u在 xz平面上的等值线图(中性曲线下分支附近)Fig.11 Contours of disturbance velocity u in the xz plane (near the lower branch of the neutral curve)

图12 扰动速度 u在 xz平面上的等值线图(中性曲线上分支附近)Fig.12 Contours of disturbance velocity u in the xz plane (near the upper branch of the neutral curve)
2.2.3 全局稳定性下的中性曲线
在不同流向波数α下进行计算,得到了如图 13的b0在Re-α面上的等值线图,即全局稳定性下的中性曲线,本文计算的流向波数范围是(0.95,1.09).从图中可以看到,最外层的线对应的是 b0=0的情况,即一般槽道流的中性曲线,并且随着b0的增大,中性曲线逐渐向下移动.

图13 b0在Re-α 平面上的等值线图Fig.13 Contours of b0in the Re-α plane
3 结论及展望
本文通过数值模拟的方法对基本流在展向周期变化的槽道流的全局稳定性问题进行了研究,得出以下主要结论.
(1) 全局稳定性下的扰动呈指数演化的形式.
(2) 展向幅值b对扰动起着稳定性作用,即随着b的增大,扰动的增长率减小,流动变得越来越稳定.
(3) 全局中性情况下各阶谐波沿法向的分布类似.
(4) 随着 b0的增大,全局稳定性下的中性曲线逐渐向下移动.
本文只给出了流向波数α范围为(0.95,1.09)的中性曲线,对于其他波数可以进一步计算,并且本文只针对展向基本波数为1.0的情况进行了研究,对于其他波数可以进行更深入的探讨.
[1] Huerre P,Monkewitz P. Local and global instabilities in spatially developing flows[J]. Annu Rev Fluid Mech,1990,22:473-537.
[2] Chomaz J. Global instabilities in spatially developing flows:Non-normality and nonlinearity[J]. Annu Rev Fluid Mech,2005,37(2):357-392.
[3] Hammond D A,Redekopp L G. Local and global insta
bility properties of separation bubbles[J]. Eur J Mech-B/Fluids,1998,17(2):145-164.
[4] Zulauf M,Hart J,Leben R,et al. Local instability in a periodically forced sliced cylinder[J]. Dynamics of Atmospheres and Oceans,1996,25(2):87-107.
[5] Monkewitz P A,Huerre P,Chomaz J M. Global linear stability analysis of weakly non-parallel shear flows[J]. Fluid Mech,1993,251(1):1-20.
[6] Crouch J,Garbaruk A,Magidov D. Predicting the onset of flow unsteadiness based on global instability[J]. Journal of Computional Physics,2007,10(2):924-940.
[7] Tezuka A,Suzuki K. The global stability analysis of steady flow around a blunted cyclinder[C]//Proceedings of the 4th Asia Workshop on Computational Fluid Dynamics. Tokyo,Japan,2004:89-94.
[8] Couairon A,Chomaz J. Global instability in fully nonlinear systems[J]. Physical Review Letters,1996,77(4):4015-4018.
[9] Dongarra J,Straughan B,Walker D. Chebyshev tau-qz algorithm method for calculating spectra of hydrodynamic stability problems[J]. Applied Numerical Mathematics,1996,22(4):399-434.
[10] 周 恒,赵耕夫. 流动稳定性[M]. 北京:国防工业出版社,2004.
Zhou Heng,Zhao Gengfu. Hydrodynamic Stability[M]. Beijing:National Defence Industry Press,2004(in Chinese).
[11] 肖红林. 槽道湍流的大涡模拟[D]. 天津:天津大学机械工程学院,2004.
Xiao Honglin. Large Eddy Simulation of Turbulent Channel Flow[D]. Tianjin:School of Mechanical Engineering,Tianjin University,2004(in Chinese).
(责任编辑:樊素英)
Numerical Simulation of Global Stability Investigation on Channel Flow with Periodical Spanwise Variation
Kong Wei,Luo Jisheng
(School of Mechanical Engineering,Tianjin University,Tianjin 300072,China)
The global stability of the channel flow with periodical spanwise variation is investigated using numerical simulation in this paper. At first,the eigenfunction of disturbance obtained by linear stability theory is given as the initial value to calculate the time development of the disturbance. Then,the eigenvalue of global stability is obtained after fully development. The results of different spanwise variation amplitudes and neutral curves in global stability are given,and detailed analysis is made on the variation of b0with the Reynolds number and the characteristics of eigenfuctions.
global stability;periodical spanwise variation;channel flow;numerical simulation
O357.1
A
0493-2137(2015)03-0246-09
10.11784/tdxbz201307029
2013-07-11;
2013-10-31.
国家自然科学基金重点资助项目(10632050);国家自然科学基金青年科学基金资助项目(11202147);高等学校博士学科点专项科研基金(新教师类)资助项目(20120032120007).
孔 玮(1986— ),男,博士研究生,kongwei203@163.com.
罗纪生,jsluo@tju.edu.cn.
时间:2013-11-22.
http://www.cnki.net/kcms/detail/12.1127.N.20131122.1101.006.html.

