基于联合振动试验系统的正弦加随机振动研究
严鲁涛,杨志鹏,王有杰
(北京强度环境研究所,北京 100076)
基于联合振动试验系统的正弦加随机振动研究
严鲁涛,杨志鹏,王有杰
(北京强度环境研究所,北京 100076)
提出联合振动试验系统,将液压振动台与电动台有效结合,并实现较大量级的正弦加随机振动。用液压台施加低频正弦激励,用电动台施加宽频随机激励,将正弦信号与随机信号有效分离,并分别用功率谱及频谱控制。设置弹性、阻尼单元,用以模拟台面至工件的传递特性,通过调整弹簧刚度及阻尼大小,使台面至工件及电动台的传递特性一致,以保护电动台。利用有限元软件Nastran仿真控制效果,将刚度、阻尼合理匹配后,电动台能较好跟踪工件运动。通过功率谱均衡方法有效控制随机振动试验,并在电动台输出端获得与目标谱较一致的功率谱。工件呈现出要求的正弦加随机振动,从而证明该系统的有效性。
联合振动;振动试验;正弦加随机;有限元分析;振动控制
振动试验为应用较广的产品测试技术,旨在考核产品经受振动激励能力及在振动激励下保持性能的能力,研究、检验振动条件下产品结构及操纵可靠性[1]。振动台为振动试验系统中的执行机构,有机械振动台、电动振动台、液压振动台等多种类型。其中电动振动台及液压振动台使用最广[2]。电动式振动台频率范围宽,但推力较小,主要用于高频及波形失真要求较高的试验领域。而电液振动台虽推力大,但存在高频性能差、上限工作频率低、波形失真大等缺点。
现有振动试验系统一般使用同种类型振动设备,往往只能实现设备允许的振动量级,大型全尺寸试件的低频大振幅振动试验常通过液压振动台实现,而宽频小振幅振动多通过电动台实现。
自然界中,正弦加随机振动或窄带加随机的混合振动环境较常见,如道路轨道车辆发动机与路面噪声,工程机械、航空航海的船舶螺旋桨冲击及海浪冲击等;军用设备如螺旋桨飞机、直升飞机、喷气机、火炮发射等。因结构损伤及疲劳破坏由随机与正弦振动共同作用的结果,其混合模式振动试验更能真实模拟或再现样品经历的真实条件[3-4]。现有文献多用正弦加随机振动试验方法对应不同试件的具体试验过程、试验夹具设计以及集中控制方法研究,以期获得更高的控制精度及运算速度[5-6]。
然而,因电动台位移幅值限制,对低频段量级较高的正弦加随机振动现有试验系统无法实现,故利用单一类型振动台模式存在限制。本文提出一种联合振动试验装置,将低、高频振动设备有效结合,综合设备优势,扩展振动试验系统使用范围。并利用有限元仿真验证该系统对大量级正弦加随机振动的适用性。
1 试验系统及动力学模型
联合振动试验系统见图1,试件整体为低频或窄带振动,而高频段部分为随机振动背景上叠加正弦或窄带随机振动试验的混合模式。电液振动台系统由液压油源、伺服阀、液压作动器及扩展台组成,提供低频大推力振动。指令信号发送至伺服阀,通过改变阀芯位置或转角改变通入缸内上下腔流量,从而改变活塞杆位置。可以看出,由于电动台位移一般较小,为保护电动台,需使扩展台至试件低频段及电动台输出杆的传递特性一致。即在扩展台激励下试件与电动台同步运动。为此,设置含可变刚度弹簧、阻尼器的传递环节。
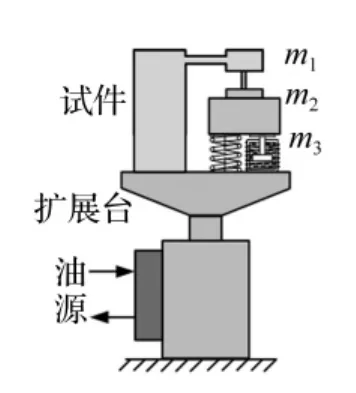
图1 试验系统Fig.1 Vibration test system
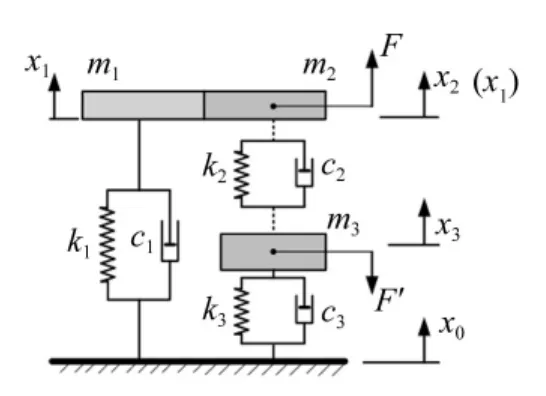
图2 动力学模型Fig.2 Dynamics model
建立系统的动力学模型见图2。电液振动台激励经扩展台、试件主体传递至元部件(见图2左半部),而高频激振器及可变刚度弹簧、阻尼器可简化为图2右半部。图中,m1为试件元部件质量;m2为电动台运动部分质量;m3为电动台静止部分质量;k1,c1分别为扩展台至试件元部件的传递刚度及阻尼;k2,c2分别为电动台静止部分至运动部分的传递刚度及阻尼;k3,c3分别为扩展台至电动台的传递刚度及阻尼;x0为扩展台激励; x1,x2,x3分别为m1,m2,m3的运动;F及F'为m2及m3的相互作用力。试验进时m1与m2固定连接,需设计系统参数使x1=x2,进行传递特性推导。
液压振动台扩展台面激励x0至x1的传递关系可由m1的运动方程获得,即

电动台运动与静止部件间基于载流导体在磁场中受电磁力作用,该电磁力与导体中电流、导体在磁场中的有效长度及导体所处磁场的磁感应强度有关。电动台固有频率一般较高,在低频段可认为刚性传递,因电磁力F数值较小,在本文动力学模型中液压台驱动为主要分析对象,忽略F影响。在x0激励下分别对m2,m3建立运动方程为
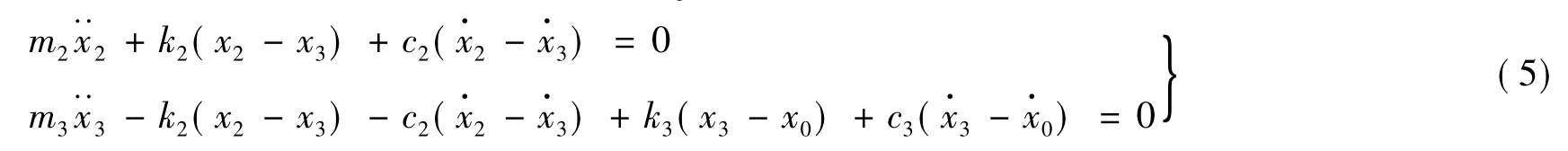
解方程组,消去x3,得x2与x0的传递关系为
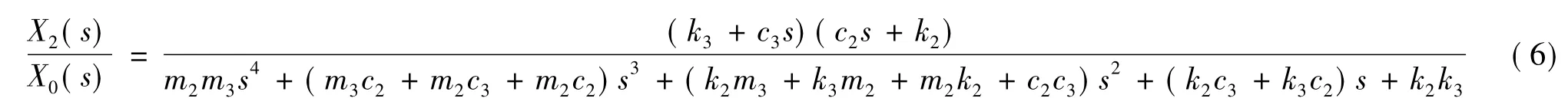

2 试验控制方法及参数匹配
2.1 试验控制方法
正弦加随机振动控制过程见图3。液压台输出激励后测试m1,m2响应,并计算传递特性,进而匹配弹性/阻尼单元。将试验谱型分离成正弦及随机振动谱型,生成正弦及随机信号分别发送至液压台、电动台;采集响应信号后将信号分离,并对正弦、随机响应信号进行幅值及功率谱密度估计;对于正弦信号幅值均衡,对随机信号做功率谱密度均衡,重新生成信号并进入循环。其中,高低频信号频谱分离可据傅里叶变换的线性性质实现,而正弦信号分离用复数二差法、基于最小二乘的幅值相位分离法、基于多分辨率谱分析的信号分离法等[5-7]。
2.2 参数匹配及验证
在扩展台激励下需使m1,m2响应一致(相近),否则会引起电动台系统位移超限。对正弦加随机或窄带加随机振动试验,结合上述系统,m2,m1未连接时,液压台发送低量级信号,采集响应信号,获得传递特性。将电动台视为刚体,据电动台质量匹配刚度、阻尼,使液压台至m1,m2的传递特性一致。
设m1=20 kg,m2=20 kg,m3=40 kg,c1=c2=5,k1=2E4,电动台试验频率至2 000 Hz,电动台刚度k2及弹性阻尼单元匹配计算式为
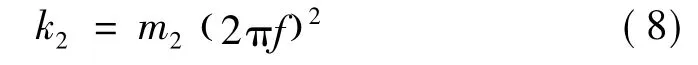
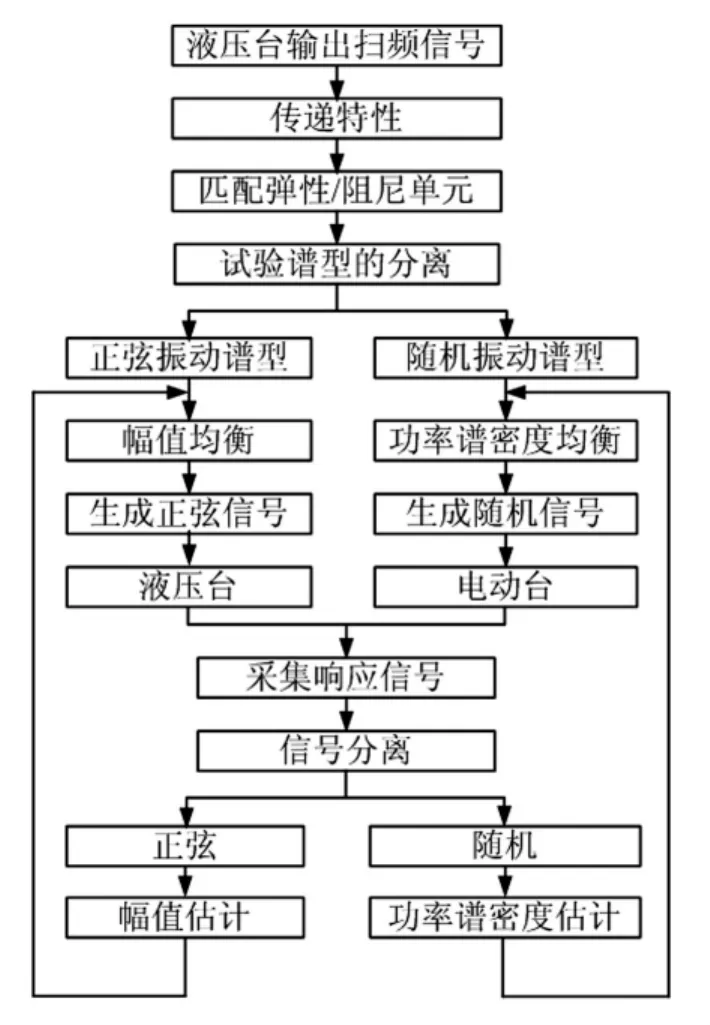
图3 控制流程Fig.3 Control process
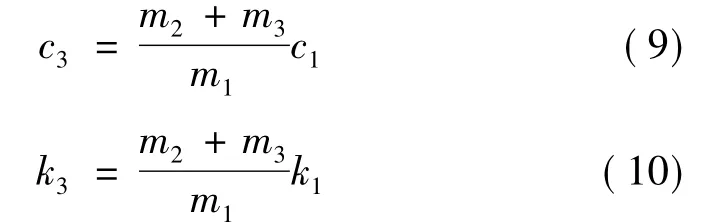
系统传递特性见图4。由图4看出,在5 Hz处出现的峰值为m1及k1构成的动力学系统固有频率。液压台的使用频率一般较低,故仅关注0~200 Hz低频段。基础对m1及m2的传递特性一致,且不存在相位差。电动台的静止质量与运动质量及弹性单元构成二自由度系统,因此在2 450 Hz处出现另一峰值。
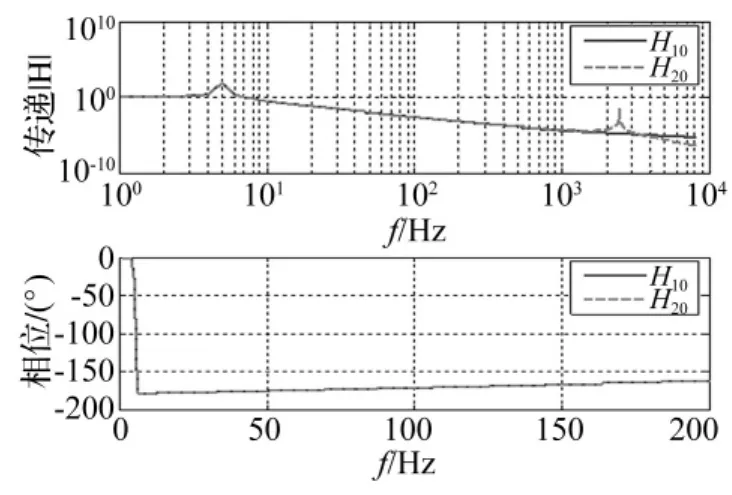
图4 系统传递特性Fig.4 Transfer properties of the system by the
设液压台输入频率为5 Hz、幅值为2 g的正弦信号,电动台输入随机噪声信号,m1,m2响应见图5。由图5看出,未加入随机时m1,m2响应相同,因激励频率与系统固有频率相等时产生共振,致响应放大,故幅值较高。
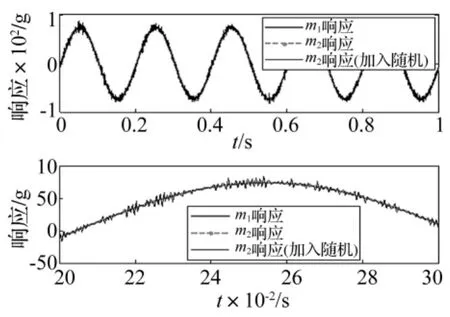
图5 m1,m2响应Fig.5 Dynamic responses of m1and m2
3 仿真分析
3.1 目标谱值及驱动信号生成
目标谱值频率范围1~2 000 Hz,底谱密度为0.02 g2/Hz,在频率5 Hz、20 Hz、45 Hz处为正弦振动,加速度幅值分别为15 g、9 g、3 g,对应位移幅值分别为149.1 mm、5.6 mm、0.4 mm。对低频段,现有电动台位移幅值无法满足;对底谱段,因频带较宽,液压台无法实现,故该谱型需液压台与电动台联合实现。液压台需驱动扩展台面、整体试件、弹性阻尼单元、电动台等,而电动台仅需驱动部分试件。
驱动信号含随机信号及正弦信号两部分。其中,随机信号的生成,据底谱值计算频谱值,进行对称变换,加入随机相位,通过IFFT变换获得伪随机信号;再经时域随机化,即延迟、倒序、加窗、搭接等过程获得真随机信号[8]。正弦信号据幅值及频率较易获得,初相位值取零。
3.2 有限元模型
有限元模型见图6,试件m1用悬臂梁(Φ60 mm,长0.5 m)表示,其阻尼特性可由几何参数及软件设置定义。悬臂梁材料为钢,弹性模量2×1011Pa,泊松比0.3,密度7 800 kg/m3。电动台运动部件质量m2及静止部件质量m3均由集中质量(m2=100 kg,m3=150 kg)单元定义,弹簧k2及k3均由线性弹簧单元表示(k2=1.6×1010,k3=8.4×106)。与台面相连的两节点(节点1、2)输入相同信号以表示相同的台面激励,m2及m3设置大小相同方向相反激励以表示电动台静止及运动部件的相对作用。
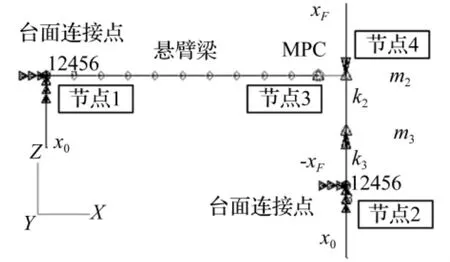
图6 有限元模型Fig.6 Finite element analysis model
3.3 正弦信号控制
为获得台面至m1的传递特性,用扫频信号进行辨识,仿真结果见图7。扫频信号参数为:扫频速率20 Hz/s,初始相位0,初始频率0.1 Hz,采样频率2 000 Hz。对应图6有限元模型,悬臂梁远端节点3、4未建立MPC关系,扫频信号输入节点1,对应输出信号为节点3的响应。明显看出,在频率点29.2 Hz处出现峰值,为悬臂梁一阶固有频率。
据传递特性可确定对应不同频率的放大倍数,5 Hz、20 Hz及45 Hz的放大倍数分别为2.107、4.837及3.246。据放大倍数计算压缩因子,获得均衡信号。将均衡信号输入节点1,节点3可得所求正弦信号,见图8。由图8看出,目标信号与输出信号值一致性较高,三个频率对应幅值误差分别为1.2%(-38 dB)、1.5% (-36 dB)、1.5%(-36 dB)
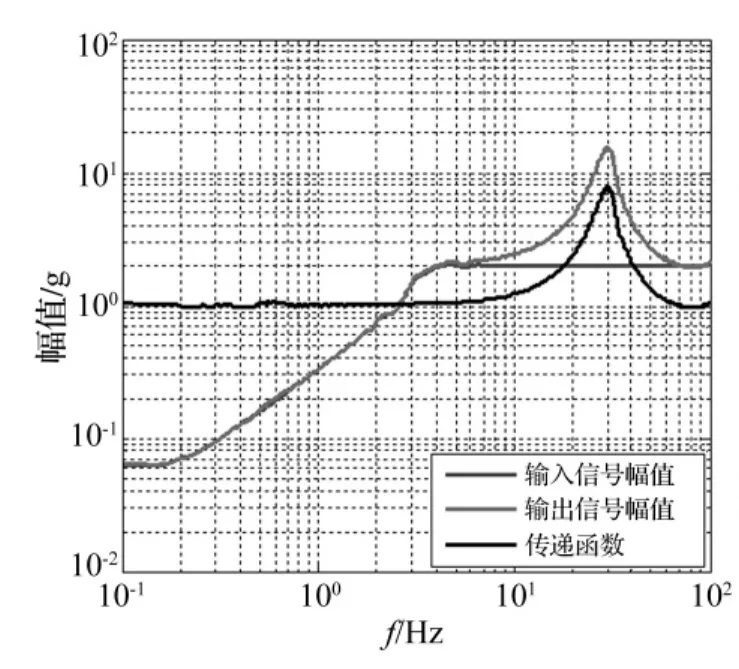
图7 扫频信号所得系统传递特性Fig.7 Transfer properties by the sweep sine signals
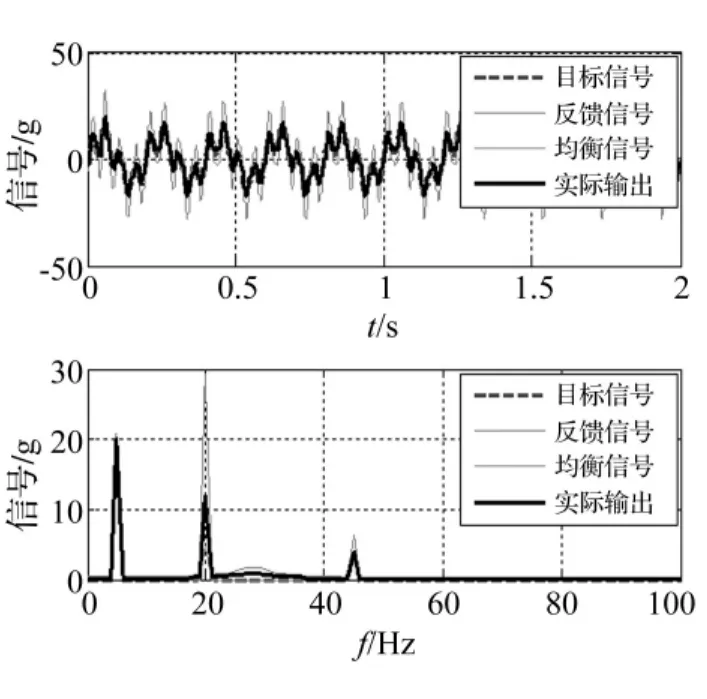
图8 正弦振动控制Fig.8 Sine vibration control
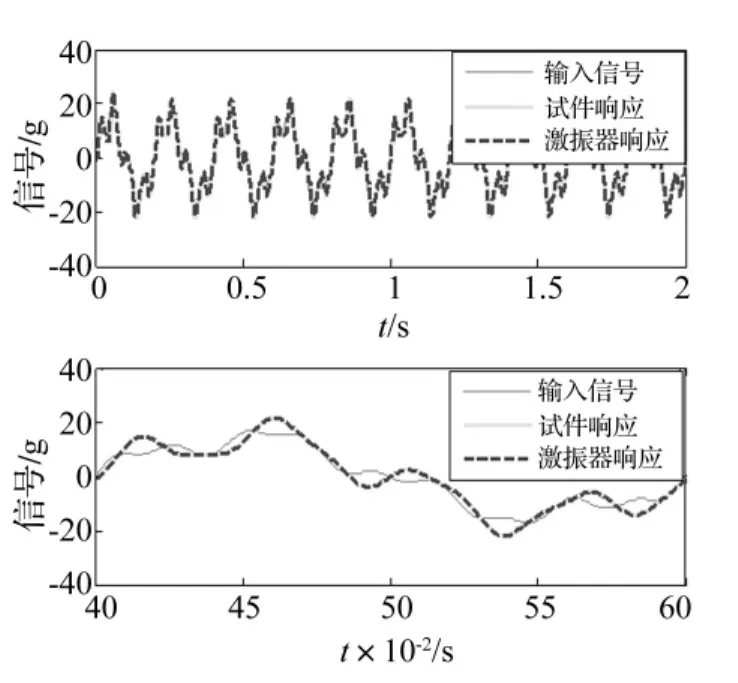
图9 响应一致性检验Fig.9 Consistency validation of the dynamic response
3.4 响应一致性分析
为避免因响应差值过大损坏电动台,在相同台面激励下,需使节点3、4响应一致。分析知需匹配合适的弹簧刚度及阻尼。按悬臂梁一阶固有频率及悬臂梁质量可计算对应刚度。因带宽直接决定共振峰陡峭程度,且带宽与阻尼成正比,可用“半功率法”求解阻尼[9]。本例中阻尼大小在软件中设置。液压台面至m2的传递环节中刚度由电动台刚度k2及设置弹簧刚度k3两部分构成。电动台刚度k2由电动台系统本身决定,为定值,故仅调整k3大小即可达到匹配精度(式(8) ~式(10))。
据正弦控制结果,对应图6中节点1、2输入相同正弦激励,仿真结果见图9。由图9看出,悬臂梁节点3响应与激振器m2响应一致性良好,说明匹配的刚度、阻尼能解决液压台面至电动台运动部分及悬臂梁远端的传递特性不一致问题。不仅能保证电动台运动部分与悬臂梁远端的随动性,亦为电动台实现宽频随机振动环境模拟提供条件。
3.5 随机振动控制
电动台激振频率范围较宽,可实现从几赫兹到上千赫兹激振,本例的随机振动环境由电动台模拟。控制过程通常为闭环功率谱均衡控制方式,据响应谱与参考谱间比较,获取对驱动谱的修正信息,采用差分法实现对驱动谱补偿,对所得新驱动谱提取其频谱信息,据系统控制要求添加相位,进行快速傅里叶逆变换产生时域驱动信号[2]。
对应图2、图6中m2,m3,k2,k3构成的二自由度系统,节点4的随机振动控制结果见图10。与图4系统特性H20趋势一致,反馈信号出现两个峰值,体现出二自由度系统的固有特性。因不存在噪声及系统非线性影响,功率谱密度经一次均衡后即达到控制精度。
3.6 联合振动模式
由于节点3、4采用MPC关联,在节点4输入随机信号后对系统控制具有一定影响。因此在系统连接后需采用正弦及随机信号分别控制。也有方法将正弦信号与随机信号叠加计算功率谱,但数字信号频域表示为离散,无法获得相邻离散点处频率幅值;而功率谱多在对数分布频域定义,傅里叶变换在频率为线性分布,正弦加随机信号功率谱值无法精确估计。另有通过增加谱线数、多分辨率等方法提高估计精度,但同样带来控制回路时间及运算量增加的问题[10]。
较实用的正弦加随机振动控制算法为分离正弦及随机信号并分别控制,将控制信号叠加。本系统中正弦、随机信号均衡后分别输送至液压台及电动台,不存在信号叠加及相互耦合问题,可避免正弦加随机信号谱估计精度差问题。经计算,响应信号及其频谱见图11,分离后的正弦、随机信号见图12。由于本系统对正弦及随机分别激励及控制,二者不存在离散点功率谱估计引起的误差。由二图看出,实际信号频谱及目标频谱非常接近,说明本方法可行。
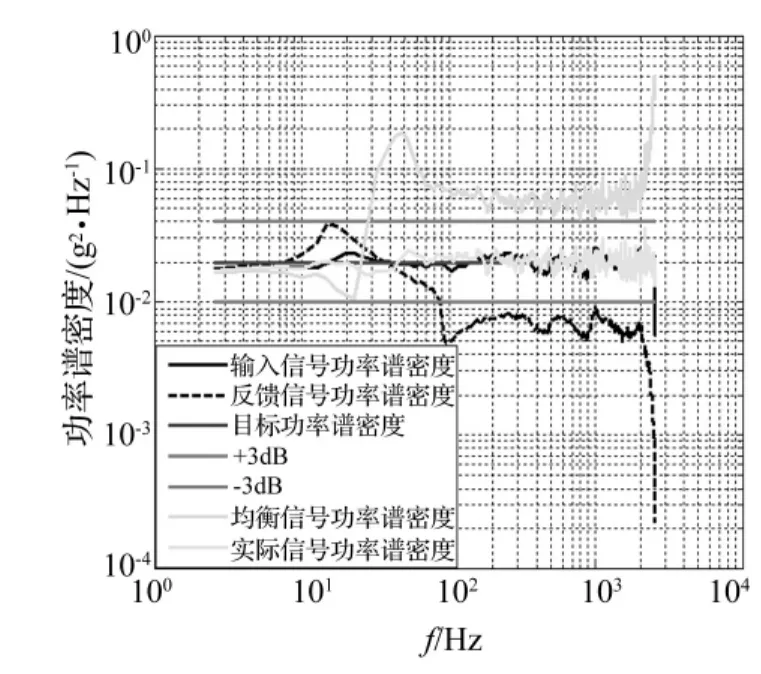
图10 随机振动控制Fig.10 Random vibration control results
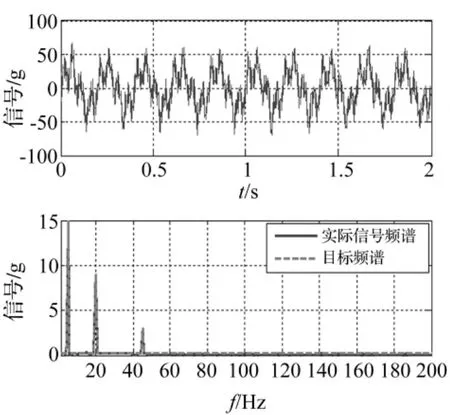
图11 响应信号及频谱Fig.11 Frequency spectrum of the response signals
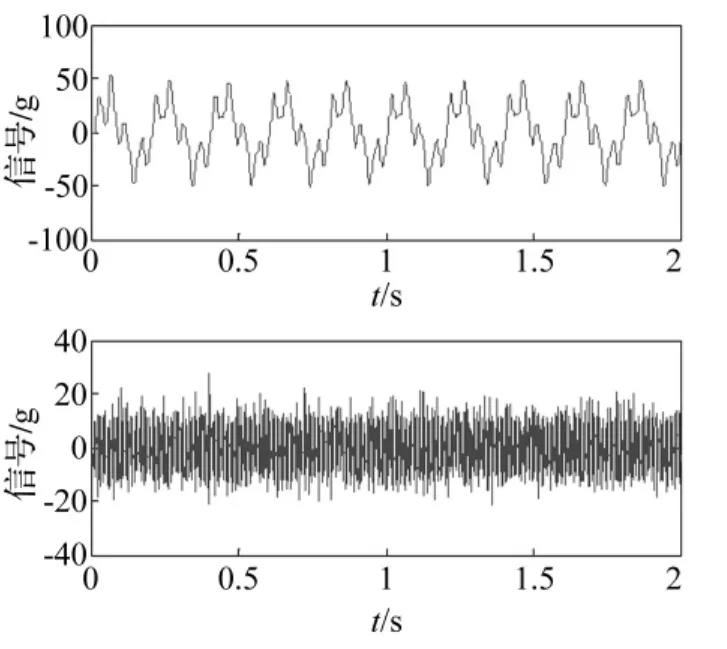
图12 信号分离Fig.12 Signals separation
4 结论
(1)提出一种联合振动试验装置,将液压振动台与电动振动台有效结合,并用于正弦加随机振动试验。
(2)系统中设置的可变阻尼及弹簧单元,可高精度模拟台面致电动台的传递特性,使电动台及试件运动一致,为电动台施加激励提供条件。
(3)将正弦加随机信号有效分离,并分别利用频谱均衡及功率谱密度均衡方式控制,达到试验要求精度。
(4)基于本系统良好的操作性,使液压台提供正弦振动,电动台产生的宽频随机振动可提高正弦加随机的试验量级。
[1]陈章位,陈家焱,贺惠农.振动试验低频控制精度的研究[J].振动与冲击,2010,29(8):31-34.
CHEN Zhang-wei,CHEN Jia-yan,HE Hui-nong.Research on control accuracy at low frequency in vibration test[J]. Journal of Vibration and Shock,2010,29(8):31-34.
[2]陈章位,于慧君.振动控制技术现状与进展[J].振动与冲击,2009,28(3):73-77.
CHENZhang-wei,YUHui-jun.Existingstateand development of vibration control technology[J].Journal of Vibration and Shock,2009,28(3):73-77.
[3]王述成.振动试验实时控制系统的研究[D].杭州:浙江大学,2006.
[4]卢兆明,周骅,李仰钞.混合振动试验在汽车电子装备中的应用和要点[J].环境技术,2009,27(2):35-41.
LU Zhao-ming,ZHOU Hua,LI Yang-chao.Mixed mode vibration test applied to electrical and electronic equipment of road vehicles[J].Environmental Technology,2009,27(2): 35-41.
[5]Stefanello M,Eng M,Carati E G.Environment for random and sinusoidalvibrationtestcontrolofaninverter-fed electrodynamic shaker[C].IEEE,2003:1093-1098.
[6]袁宏杰,李传日.正弦加随机振动控制技术的研究[J].航空学报,2000,21(4):383-384.
YUAN Hong-jie,LI Chuan-ri.Study of the sine-on-random vibration control[J].ACTA Aeronauticaet Astronautica Sinica,2000,21(4):383-384.
[7]陈后金,胡健,薛健.信号与系统[M].北京:清华大学出版社,2003.
[8]胡志强,法庆衍,洪宝林,等.随机振动试验应用技术[M].北京:中国计量出版社,1996:131-135.
[9]顾海明,周勇军.机械振动理论与应用[M].南京:东南大学出版社,2007.
[10]王述成,陈章位.基于多分辨率谱分析的正弦加随机振动试验控制算法的研究[J].中国机械工程,2005,16(15):1335-1338.
WANG Shu-cheng,CHEN Zhang-wei.A new algorithm for sine on random vibration test based on multirate spectrum estimation[J].ChinaMechanicalEngineering,2005,16(15):1335-1338.
Sine on random vibration based on combined vibration test system
YAN Lu-tao,YANG Zhi-peng,WANG You-jie
(Beijing Institute of Structure and Environment Engineering,Beijing 100076,China)
In order to increase the range of vibration frequencies,a novel combination of the hydraulic vibration table and the electrodynamic shaker was proposed.The joint test system has been used in sine on random vibration test. The sine signals and random signals were provided by the hydraulic and electrodynamic shaker respectively,and the control algorithms based on spectrum equalization and power spectral density(PSD)equalization were utilized.The variable spring-damping elements were set to simulate the transfer properties from the table to the electrodynamic shaker. Based on the simulation results by the MSC(Nastran)software,it is indicated that the dynamic characteristics of electrodynamic vibration shaker is closely related to the low frequency part of test article.In accordance with the random and sine signals,the control algorithms can continuously update the drive signals,and the control accuracy of the reproduced PSD at the control point is quite satisfactory.
combined vibration;vibration test;sine on random signal;finite element analysis;vibration control
TB535;O324
A
10.13465/j.cnki.jvs.2015.02.016
2013-09-23修改稿收到日期:2014-01-09
严鲁涛男,博士,工程师,1984年2月生

