循环荷载作用下钢梁临界侧向长细比研究

刘洋，童乐为

(同济大学土木工程学院建筑工程系土木工程防灾国家重点实验室，上海 200092)

循环荷载作用下钢梁临界侧向长细比研究

刘洋，童乐为

(同济大学土木工程学院建筑工程系土木工程防灾国家重点实验室，上海 200092)

针对我国《建筑抗震设计规范》推荐的临界侧向长细比计算公式来源于单调荷载研究结果，并未反映不同抗震等级影响问题，基于抗震等级应与适宜的转动能力相匹配准则，对循环荷载作用下钢梁进行非线性有限元分析。所建模型考虑初始几何缺陷、残余应力影响，并得到试验验证。通过对钢梁端部弯矩比、腹板高厚比、翼缘宽厚比、残余应力分布图式及平面外边界约束条件等5类影响因素数值分析，提出循环荷载作用下钢梁临界侧向长细比计算公式。该公式具有计算精度高、表达形式简单等特点。

钢梁;抗震设计;临界侧向长细比;循环荷载;抗震等级;转动能力;端部弯矩比

抗震设计中，多、高层钢结构框架横梁侧向长细比l应小于临界侧向长细比lcr，防止发生过早整体失稳，保证产生塑性铰截面具有足够的转动能力。其中，l= l/ry，l为钢梁侧向支撑点间距离;ry为钢梁弯矩作用平面外回转半径。GB 50011－2010《建筑抗震设计规范》(下称抗震规范)及GB 50017－2003《钢结构设计规范》(下称钢规)中临界值lcr计算式为

式中:M1为产生塑性铰的截面弯矩;M2为塑性铰距l侧向支承点处截面弯矩，二者均以顺时针为正;M2/M1称端部弯矩比，使钢梁同曲率弯曲的M2/M1为正，使钢梁反曲率弯曲的M2/M1为负。

式(1)由梁启智［1］最早提出，适用于钢梁的塑性设计。而用于钢梁抗震设计则存在不合理:

(1)图1的转动能力定义［1］为

式中:θmax为截面所受弯矩峰值对应转角;θy为钢梁受压翼缘屈服对应转角。

美国ANSI/AISC360－05《钢结构设计规范》(下称美国钢规)采纳图1的Galambos［2］转动能力定义为

式中:θp为在纯钢梁全截面塑性弯矩Mp作用下按完全弹性抗弯刚度计算的截面转角。θu为纯弯曲截面外加弯矩下降至0.95Mp时截面转角;其它受力的θu为截面外加弯矩下降至Mp时截面转角。

文献［3－8］采用Galambos的转动能力定义，分析钢梁、组合梁及不锈钢梁的变形性能。文献［9－12］用该转动能力定义评价构件转动变形能力大小。

(2)文献［1］借鉴White等［13－14］研究，采纳构件所需转动变形φ≤10的结论，据构件转动能力大于需求转动要求，既Rc≥φ确定Rc=10的量化标准。该标准要求较高，偏于保守。美国钢规采用Galambos的普通结构φ≤3结论，据Rc≥φ要求确定R=3的量化标准。R=3标准因符合实际，更加合理而被普遍采用。

抗震等级越高对构件R要求越大。因此，李海峰等［15］借鉴Mazzolani［16］构件延性研究，提出我国构件各级抗震等级R的定量判别标准，即:一级抗震R=6，二级抗震R=4.5，三级、四级抗震R=3。式(1)计算的λcr，未体现抗震等级对构件R要求不同的差别。

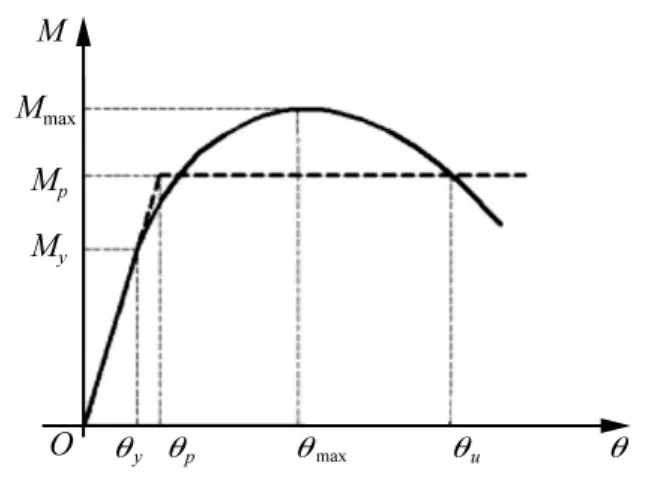
图1 转动能力定义Fig.1 Definition of rotation capacity

(3)式(1)的推导基于Janss［17］的试验数据。该试验的单调加载与地震作用下循环加载有差别。Masayoshi等［18－19］研究发现循环荷载作用下钢梁的R低于单调荷载作用。故式(1)用于抗震设计不合理。

(4)Kemp等［3－4，20］认为截面板件宽(高)厚比对λcr有一定影响，但式(1)未能反映板件宽厚比对λcr的影响。

综上所述，抗震设计时亟需一种合理可靠的λcr计算公式。为此，本文按不同抗震等级采用不同R标准，即一级抗震R=6，二级抗震R=4.5，三级、四级抗震R =3，对循环荷载作用的钢梁进行有限元非线性分析。通过对端部弯矩比、腹板高厚比、翼缘宽厚比、残余应力分布形式及平面外边界条件等5类影响因素研究，提出循环荷载作用下钢梁λcr计算公式，用于工程设计。

1 有限元模型建立及验证

1.1 有限元模型建立

平面内简支梁计算模型见图2。对梁两端施加弯矩。钢梁材料Q235，截面为H型钢，腹板高hw=400 mm，翼缘宽b=200 mm，tw，tf由板件宽厚比取值确定。钢梁长l由其侧向长细比λ取值确定。

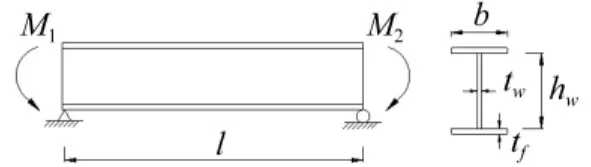
图2 计算简图Fig.2 Calculation model

选择5类参数进行分析:端部弯矩比M2/M1、腹板高厚比hw/tw、翼缘宽厚比b/2tf、残余应力分布形式及端部平面外边界条件。各类参数选择如下:

(1)考虑3种端部弯矩比，即M2/M1为1、0、－1，见图3。

(2)据我国钢规，用于塑性设计的工字型截面板件宽厚比限值为:①受压翼缘宽厚比b/2tf=9;②受弯腹板高厚比hw/tw=72。本文b/2tf取值分别为9、7、5，hw/tw取值分别为72、54、36，排列组合共9种截面。板件宽厚比、高厚比取值变化通过保持hw、b不变，改变tw、tf实现。

(3)H型钢截面残余应力分布因工字钢梁制作工艺不同而有差别，见图4。考虑3种常见残余应力分布，即轧制梁截面残余应力、翼缘板边焰割的焊接梁截面残余应力、翼缘板边为轧制边的焊接梁截面残余应力。

图3 弯矩工况Fig.3 bending moment cases

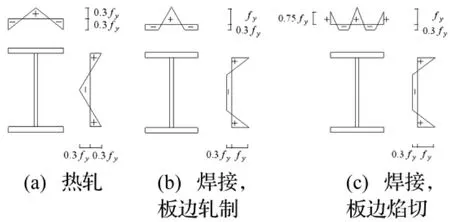
图4 H形钢截面残余应力分布图式Fig.4 Residual stress distribution pattern of H－shaped steel cross section

(4)考虑两种端部平面外边界条件:简支与固支。

(5)上述4类参数对侧向长细比λ的取值影响显著。因此不同参数下，λ取值有差异，见表1。

表1 有限元分析考虑的侧向长细比λTab.1 Lateral slenderness ratio λ considered in FEA

钢材用随动强化模型，应力－应变曲线见图5。其中屈服强度fy=235 MPa，据我国钢规中塑性设计规定，抗拉强度fu应大于1.2fy，故本文的fu=1.3 fy，弹性模量E=2.06×105MPa，切线模量Est=E/100。

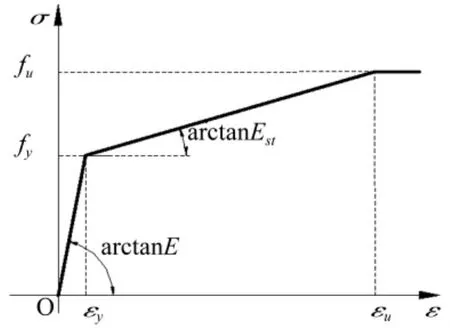
图5 钢材应力－应变曲线Fig.5 Stress－strain curve for steel

用有限元软件ABAQUS建模，有限元模型见图6，由钢梁与端部刚性板两部分组成。建立端部刚性板目的为方便施加端部弯矩荷载。考虑完全积分在大弯曲变形下会产生剪力自锁效应，钢梁选缩减积分壳单元S4R，刚性板选刚体单元R3D4。刚性板与钢梁端部间用绑定命令，便于端部荷载顺利传递到梁上。

图6 有限元模型Fig.6 Finite element model

本文采用特征值分析所得第一阶屈曲模态乘以初始缺陷系数模拟实际构件的初始缺陷。据《钢结构工程施工质量验收规范》规定，初始缺陷系数取l/1 000与b/100两者最大值。

1.2 加载制度

循环加载制度见图7。由图7可见:

(1)在M1作用端部施加转角θ1，当θ1＜θy时有一级循环1次，幅值为0.5θy;当θ1≥θy时每级循环3次，每级幅值增加θy，其中θy为钢梁屈服转角。

(2)在M2作用端部施加转角q2，q2的加载制度与θ1相同，θ2取值受荷载工况影响，即M2/M1=1时θ2= θ1;M2/M1=0时θ2=0;M2/M1=－1时θ2=－θ1。

据材料力学基本理论，屈服转角θy为

式中:h为钢梁截面总高度。

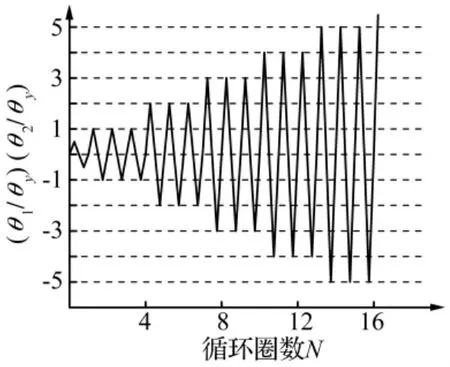
图7 数值分析中所用加载制度示意图Fig.7 Sketch of cyclic loading regime in numerical analysis

1.3 有限元模型验证

对Okazaki［21］的试验进行有限元数值模拟，验证本文有限元模型的可靠性。该试验通过加载梁施加水平循环位移，模拟两品框架梁在地震荷载作用下效应，柱子为刚性柱，用于实现水平位移滞回加载转化为对梁端部转角的滞回加载，见图8。试验梁总高度h=70 mm，翼缘宽b=30 mm，腹板厚度tw=2 mm，翼缘厚tf=3 mm，长l=810，侧向长细比为121。试验梁受力工况M2/M1=－1。试验加载机制用梁端部转角θ形式表达，分3级，每级2次，各级幅值为0.02 rad、0.04 rad、0.06 rad，见图9。有限元分析与Okazaki试验［21］弯矩－转角滞回曲线比较见图10。由图10可见，两条曲线吻合较好，由此已验证本文有限元模型的正确性。

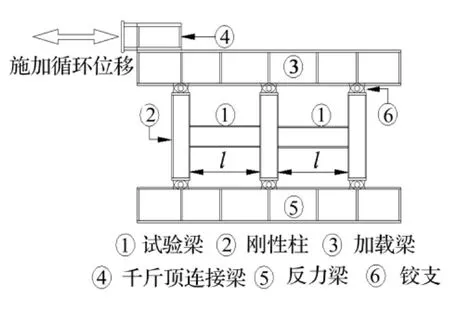
图8 Okazaki试验装置［21］Fig.8 Setup in Okazaki＇s test［21］

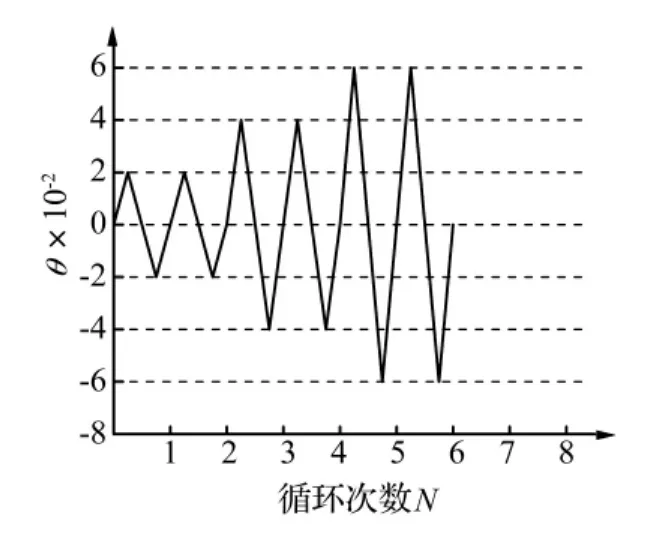
图9 Okazaki试验［21］加载制度示意图Fig.9 Sketch of cyclic loading regime in Okazaki＇s test［21］

图10 有限元分析与Okazaki试验［21］弯矩－转角滞回曲线比较Fig.10 Comparison in moment－rotation hysteretic curves between FEA and Okazaki＇s test［21］

2 确定临界侧向长细比方法

在循环荷载作用下需提取钢梁骨架曲线，在骨架曲线基础上，按Galambos的R定义分别求出R+(正向骨架曲线得出)、R－(负向骨架曲线得出)，最终R取R+与R－的平均值，见图11。

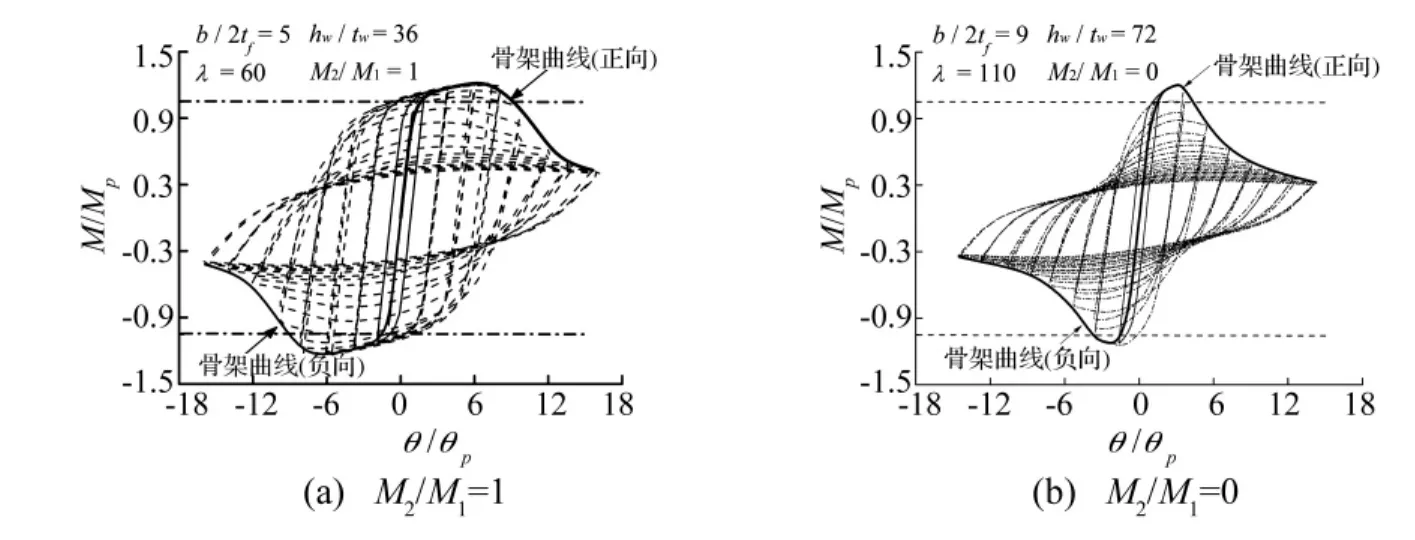
图11 本文有限元分析所得钢梁弯矩－转角滞回曲线Fig.11 Relationship curve between moment ratio and rotation capacity by FEA

图12 侧向长细比与转动能力关系Fig.12 Relationship between lateral slenderness ratio and rotation capacity

钢梁(截面为b/2tf=5，hw/tw=54，平面外边界条件固支)在3种工况下的λ与R关系见图12。由图12看出，在给定的M2/M1作用下，λ愈大R愈小，两者呈递减关系。其它钢梁截面均符合此规律。限于篇幅不再给出。在该规律基础上，本文采用线性插值方法［1］，即一级R=6，二级R=4.5，三、四级R=3作为确定临界侧向长细比λcr标准，所得相应λcr数值见表2～表4。

表2 临界侧向长细比λcr计算值(R=3)Tab.2 Calculated values of critical lateral slenderness ratio λcr

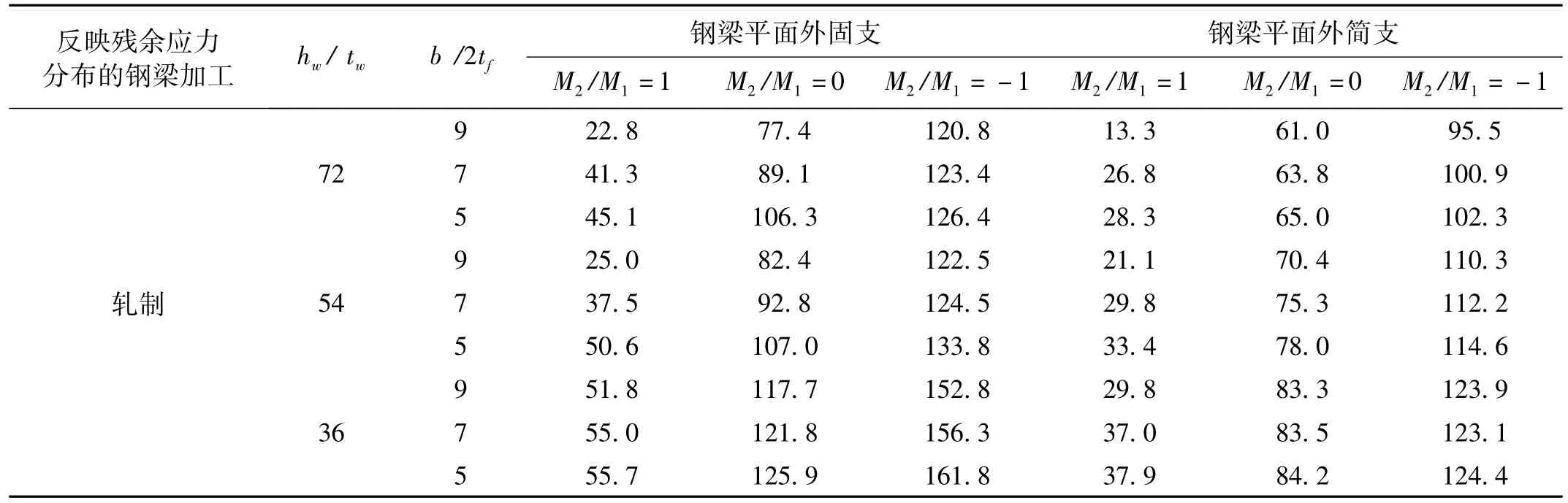
表3 临界侧向长细比λcr计算值(R=4.5)Tab.3 Calculated values of critical lateral slenderness ratio λcr

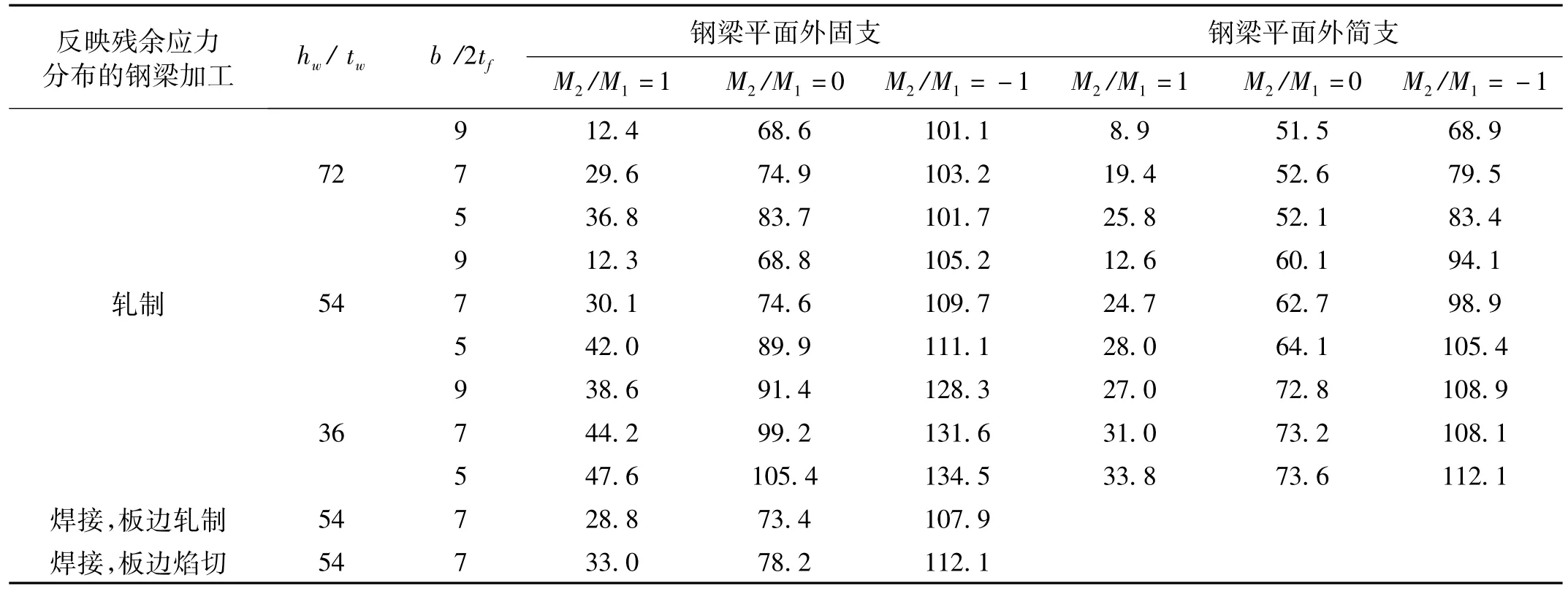
表4 临界侧向长细比λcr计算值(R=6)Tab.4 Calculated values of critical lateral slenderness ratio λcr

3 有限元参数效应分析

3.1 端部弯矩比对λcr影响

循环荷载作用下M2/M1与λcr关系曲线见图13。由图13可见，M2/M1从1变化到－1，λcr逐渐增大。因M1作用端至反弯点长度λe逐渐减少，钢梁发生整体失稳可能性降低，承载力提高，转动能力R增强，故λcr增大。

图13 端部弯矩比对λcr影响Fig.13 Influence of bending moment ratio between two ends on λcr

3.2 腹板高厚比

腹板高厚比hw/tw对λcr影响见图14。由图14可见，①λcr随hw/tw的减小而增大;②在hw/tw的54～ 72(塑性设计限值)范围内对λcr影响不明显，而在hw/tw小于54(72的75%)范围内对λcr值影响显著。

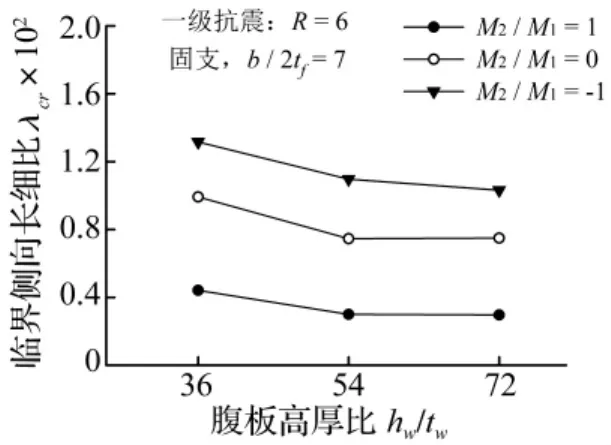
图14 腹板高厚比对λcr影响Fig.14 Influence of web height－thickness ratio on λcr

3.3 翼缘宽厚比

翼缘宽厚比b/(2tf)对λcr影响见图15。由图15看出，①λcr随b/(2tf)的减小而增大;②由图15(a)、(b)知，当hw/tw为72、54时，在M2/M1=1、0下b/2tf对λcr影响显著;在M2/M1=－1下b/2tf对λcr影响较小;③由图15(c)知，当hw/tw=36时M2/M1从1～－1，b/2tf对λcr影响较小。

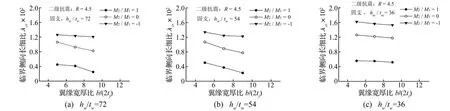
图15 翼缘宽厚比对λcr影响Fig.15 Influence of flange width－thickness ratio on λcr

3.4 残余应力分布

残余应力分布对lcr影响见图16。由图16看出，①截面焊接且翼缘板边轧制钢梁的λcr较轧制钢梁的λcr略低，因翼缘板边轧制，板边形成较大受压区，不利于平面外稳定。②截面焊接且翼缘板边焰切钢梁的λcr较轧制钢梁的λcr略高，因翼缘板边焰切，板边形成受拉区，利于平面外稳定。③在循环荷载作用下，残余应力分布对λcr影响较小，可统一采用轧制钢梁的λcr值作为3种残余应力分布钢梁的临界值。

图16 残余应力分布对λcr影响Fig.16 Influence of residual stress distribution on λcr

3.5 抗震等级

抗震等级越高，R要求越大，λcr越小。不同抗震等级下λcr比值见表5。由表5看出，λcr，R=4.5/λcr，R=6约为1.2，λcr，R=3/λcr，R=6约为1.4。

3.6 平面外边界条件

平面外边界约束条件对λcr影响见图17。由图17可见，在循环荷载作用下，平面外简支钢梁临界长细比λcr，s值小于平面外固支钢梁临界长细比λcr，f值，因平面外简支钢梁的面外有效长度大于平面外固支钢梁，不利于钢梁的面外稳定性，故其极限承载力低，转动能力弱。

表5 不同抗震等级λcr比值Tab.5 Ratio of λcrfor different seismic grade

图17 平面外边界条件影响Fig.17 Influence of out－of－plane constraint conditions

λcr，s与λcr，f的比值基本在70%以上，见表6～表8。故可采用平面外固支钢梁λcr，f值的70%作为平面外简支钢梁的λcr，s值。

表6 λcr，s与λcr，f之比(R=3)Tab.6 Ratio of λcr，sand λcr，f

表7 λcr，s与λcr，f之比(R=4.5)Tab.7 Ratio of λcr，sand λcr，f

表8 λcr，s与λcr，f之比(R=6)Tab.8 Ratio of λcr，sand λcr，f

3.7 循环荷载作用下板件宽厚比限值

工况M2/M1=1且R=6、4.5时λcr分布见图18。由图18看出，在循环荷载作用下，平面外或固支、或简支，b/2tf在0～9、hw/tw在0～72范围内均存在一些截面的钢梁λcr偏小。如对平面外简支、转动能力R=6，b/2tf=9、hw/tw=72的截面其λcr=8.9;对b/2tf=9、hw/tw=54的截面其λcr=12.6。一般而言，当λcr＜20时被认为截面板件宽(高)厚比取值过大，不宜采用，钢梁截面设计时应对板件宽厚比进行限制。

图18 M2/M1=1时λcr分布Fig.18 Distribution of λcrratio for M2/M1=1

由于平面外简支钢梁板件的宽厚比限值更严格，故从保守、方便设计角度考虑，平面外固支钢梁可采用与平面外简支钢梁相同的板件宽厚比限值。通过对图18分析、归纳，并结合钢规板件宽(高)厚比限值规定，本文给出M2/M1＜0时达到所需转动能力的钢梁板件宽厚比限值表达式为

对一、二级抗震，M2/M1≥0及三、四级抗震所有工况，hw/tw、b/2tf限值应按我国抗震规范、钢规中塑性设计的规定设置。

4 计算公式拟合

据钢梁λcr随主要因素变化规律，本文考虑参数hw/tw影响，以为界分成两个表达式，提出含主要参数M2/M1的λcr计算公式。在0.5＜M2/M1≤1范围内，据式(1)特点(我国钢规λcr计算公式)，即当0.5＜M2/M1≤1时λcr的增长变化较小，从安全角度出发，λcr计算公式采用M2/M1=1时的λcr作为范围内λcr值。在－1≤M2/M1≤0.5范围内λcr计算公式采用M2/M1的二次多项式计算λcr，以提高计算精度。公式引入修正系数以考虑抗震等级及平面外边界条件影响。λcr计算式为

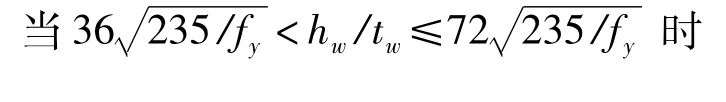
式中:a1为抗震等级影响系数，一级抗震a1=1，二级抗震a1=1.2，三、四级抗震a1=1.4;a2为平面外边界条件影响系数，平面外固支时a2=1，平面外简支时a2= 0.7。

图19表明式(7)、(8)计算结果与有限元结果差异较小，吻合较好，且有限元计算结果基本在公式曲线以上，说明本文所提公式精度高、可靠性好，可用于工程设计。

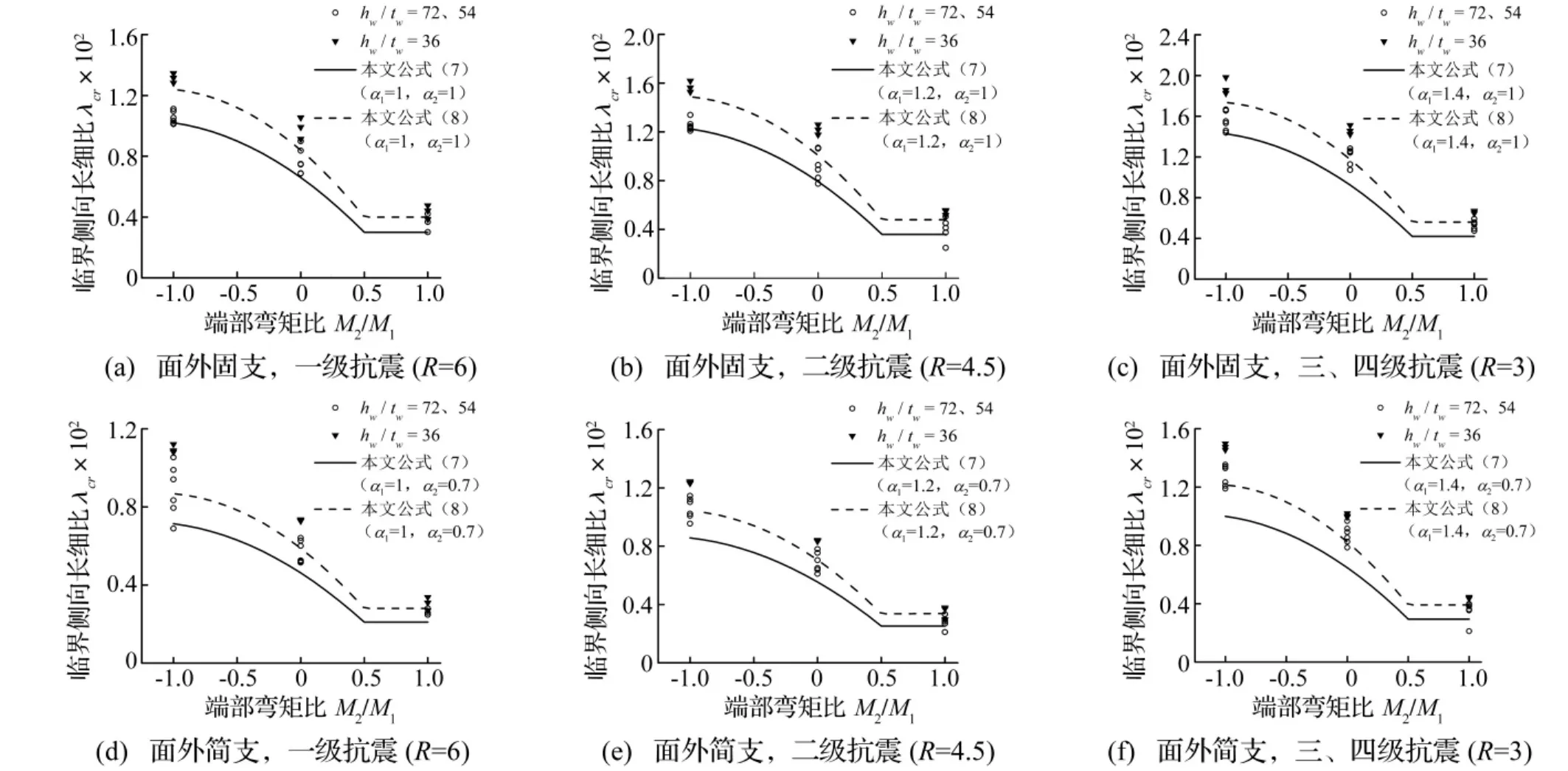
图19 本文简化公式计算值与有限元计算值比较Fig.19 Comparison of calculated values from the proposed formulas in this paper and FEM

5 结论

本文通过对循环荷载作用下的钢梁进行非线性分析，基于抗震设计要求研究影响钢梁临界侧向长细比λcr主要因素，结论如下:

(1)循环荷载作用下，端部弯矩比M2/M1从1(纯弯受力)变化到－1时λcr逐渐增大，与单调荷载作用下钢梁规律一致。

(2)λcr随hw/tw的减小而增大。在hw/tw从54～ 72(塑性设计限值)范围内(塑性设计限值)时其对λcr影响不明显，而在hw/tw＜54(72的75%)范围内其对λcr值影响显著。

(3)λcr随b/2tf的减小而增大。当hw/tw为72、54时，在工况M2/M1=1、0下，b/2tf对λcr影响显著;在M2/M1=－1下，b/2tf对λcr影响较小。当hw/tw=36时，M2/M1从1～－1，b/2tf对λcr影响较小。

(4)循环荷载作用下钢梁残余应力的不同分布对λcr影响较小，可采用统一的λcr。

(5)抗震等级要求越高λcr越小。当一级抗震的λcr为λcr，R=6，二级抗震的λcr为λcr，R=4.5，三、四级抗震的λcr为λcr，R=3时，λcr，R=4.5/λcr，R=6约为1.2;λcr，R=3/ λcr，R=6约为1.4。

(6)平面外边界约束条件对λcr影响显著，简支钢梁的λcr约为固支钢梁值的70%。

(7)工况M2/M1=1、一些截面的λcr＜20时不宜采用，应限制截面板件宽(高)厚比。本文已给出板件宽厚比限制范围。

(8)本文提出含钢梁端部弯矩比M2/M1及hw/tw比两个重要参数、并考虑抗震等级差别的λcr计算公式，并设置修正系数以考虑平面外边界约束条件影响。

［1］梁启智.关于钢梁设计中考虑塑性的问题［J］.华南工学院学报，1978，6(4):20－31.

LIANG Qin－zhi.Plastic design of steel beams［J］.Journal of South China University of Technology，1978，6(4):20－31.

［2］Galambos T V.Deformation and energy absorption capacity of steel structures in the inelastic range［R］.New York: American IronandSteelInstitute，SteelResearchfor Construction Bulletin No.8，1968:1－49.

［3］Kemp A R.Interaction of plastic local and lateral buckling［J］.Journal of the Structural Division，1986，111(10):2181－2196.

［4］Kemp A R.Available rotation capacity in steel and composite beams［J］.The Structural Engineer，1991，69(5):88－97.

［5］Johnson R P.Distortional lateral buckling of continuous composite beams［C］.//Proceedings of the institution of civil engineers，London:Thomas Telford Services ltd，1991: 131－161.

［6］Earls C J.Constant moment behavior of high－performance steel I－shaped beams［J］.Journal of Constructional Steel Research，2001，57(7):711－728.

［7］Chan T M，Gardner L.Bending strength of hot－rolled elliptical hollowsections［J］.JournalofConstructionalStee1 Research，2008，64(9):971－986.

［8］Theofanous M，Chan T M，Gardner L.Flexural behaviour of stainlesssteelovalhollowsections［J］.Thin－Walled Structures，2009，135(5):546－557.

［9］李军强.单轴对称工字形截面塑性设计的腹板高厚比研究［D］.西安:西安建筑科技大学，2008.

［10］刘洋，童乐为.塑性设计中钢梁临界侧向长细比的研究［J］.工业建筑，2014，496(44):132－139.

LIU Yang，TONG Le－wei.Critical lateral slenderness ratio of steel beams in plastic design［J］.Industrial Construction，2014，496(44):132－139.

［11］刘洋，童乐为.钢－混凝土组合梁负弯矩区转动能力的数值分析［C］.//第十二届全国现代结构工程学术研讨会论文集(《工业建筑》增刊)，北京:工业建筑杂志社，2012: 976－981.

［12］贾远林，陈世鸣.预应力组合梁负弯矩作用下梁端转动能力研究［J］.河北工程大学学报，2009，26(1):14－20.

JIA Yuan－lin，CHEN Shi－ming.Study on rotation capacity of prestressed composite girders under negative moment［J］. Journal of Hebei University of Engineering，2009，26(1):14－20.

［13］White M.The lateral－torsional buckling of yielded structural steel members［D］.Bethleherm:Lehigh University，1956.

［14］Lay M G，Galambos T V.Inelastic steel beams under uniform moment［J］.Journal of the Engineering Mechanics Division，1965，91(6):67－94.

［15］李海锋，罗永峰，李德章，等.反复水平荷载作用下偏心常轴压箱形钢柱抗震性能的数值分析［J］.工程力学，2013，30(6):98－106.

LI Hai－feng，LUO Yong－feng，LI De－zhang，et al.Numerical analysis on a seismic behavior of eccentrically constantcompressed steel box column under cyclically lateral loading［J］.Engineering Mechanics，2013，30(6):98－106.

［16］Mazzolani F M，Piluso V.Member behavior classes of steel beams andbeam－columns［C］.//Viareggio:InXIV Congresso CTA，1993.

［17］Janss J，Massonnet C.The extension of plastic design to steel A 52［J］.Publication of IABSE，1967，27:15－30.

［18］Nakashima M，Kanao I，Liu D.Lateral instability and lateral bracing of steel beams subjected to cyclic loading［J］.Journal of Structural Engineering，2002，128(10):1308－1316.

［19］Takanashi K.Inelastic lateral torsional buckling of steel beams subjected to repeated and reversed loading［C］.//5th World Conf.on Earthquake Engineering，Rome，1973.

［20］EL－Ghazaly H A，Sherbourne A N，Dubey R N.Inelastic interactive distorsional buckling of W－shape steel beams［J］. International Journal of Computers and Structures，1983，19(3):351－368.

［21］Taichiro O，Liu D W.Stability requirements for beams in seismic steel moment frames［J］.Journal of Structural Engineering，2006，132(9):1334－1342.

Critical lateral slenderness ratio of steel beams subjected to cyclic loading

LIU Yang，TONG Le－wei
(State Key Laboratory for Disaster Reduction in Civil Engineering，Department of Building Engineering，College of Civil Engineering，Tongji University，Shanghai 20092，China)

The behavior of steel beams under cyclic loading is quite different from that under monotonic loading. However，the formula for critical lateral slenderness ratio recommended in the current Chinese code GB50011－2010 for seismic design of buildings is resulted from research findings for monotonic loading.At the same time，the effect of different seismic grades is not considered in the formula.So it is necessary to be improved.In the paper，the nonlinear finite element analysis of steel beams subjected to cyclic loading was carried out based on the concept that a seismic grade should match a suitable rotation capacity.In the model developed，the influence of initial geometric imperfection and residual stresses was taken into account and validated by other researcher＇s experimental results.By means of the numerical analysis on five parameters，namely，end－moment ratio，web height－thickness ratio，flange width－thickness ratio，residual stress distribution pattern，out－of－plane boundary condition，the formula for critical lateral slenderness ratio of steel beams under cyclic loading was proposed，with higher accuracy and simpler form.

steel beam;seismic design;critical lateral slenderness ratio;cyclic loading;seismic grade;rotation capacity;end－moment ratio

TU391

A

10.13465/j.cnki.jvs.2015.02.006

国际钢铁协会(IISI)Living Steel基金宝钢钢结构住宅项目

2014－05－10修改稿收到日期:2014－08－29

刘洋男，博士生，1982年生

童乐为男，教授，博士生导师，1961年生邮箱:tonglw@tongji.edu.cn