运行核电设施在爆破振动激励下新安全标准探讨
郭涛,谢全民,刘强,范磊,沈蔚
(1.解放军理工大学野战工程学院,南京 210007;2.武汉军械士官学校,武汉 430075)
运行核电设施在爆破振动激励下新安全标准探讨
郭涛1,谢全民2,刘强1,范磊1,沈蔚1
(1.解放军理工大学野战工程学院,南京 210007;2.武汉军械士官学校,武汉 430075)
针对我国核电基地即将或正在扩建、而前端基础开挖所用爆破产生的振动危害效应会威胁核电设施安全问题,基于分形理论开展核电扩建工程中爆破振动新安全标准探讨,研究成果对进一步规范、约束在运行核电设施附近实施工程爆破方法具有指导意义,为制定国家核电安全规划及确保我国核电安全、高效发展奠定重要基础。
爆破振动;核电设施;安全标准;分形
据我国《核电发展专题规划(2005-2020年)》,未来13年将新投产2300万千瓦核电站,标志大量核电新建、扩建工程逐步展开,其基础开挖多采用爆破方法。近年来随爆破基础理论不断突破、计算机技术广泛运用、爆破器材迅速革新及施工机械化、自动化水平提高,精细爆破理论基础与技术条件取得较大进展[1],爆破质量及安全已有一定提高,但仍难完全实现对炸药爆炸能量释放过程的精确控制,致工程爆破在实现预期工程目的时会有一部分爆炸能量转化为危害对周围环境产生不利影响,其中以振动危害效应为主,直接威胁运行核电设施安全。
运行核电设施结构所处位置与附近扩建工程中爆破施工产生的地震波作用范围重合概率较大。相对新建核电站爆破施工及一般工程爆破施工而言,在已运行或正进行试运行的核电机组附近进行爆破施工时,为确保核岛、常规岛、主控机房、网控楼等重要核电设施的安全,须对爆破振动效应提出非常严格的控制要求[2]。
考虑到核电施工中爆区环境的复杂性、爆破作用次数多重性、作用方向随机性及爆破地震波传播场地介质多样性,使爆破振动对运行核电设施影响非常复杂。本文提出一套基于分形理论的爆破振动安全标准,并通过核电扩建工程中大量实测数据对该标准科学、合理性进行充分验证,研究成果对进一步规范、约束在运行核电设施附近实施工程爆破的方法具有指导意义,为制定国家核电安全规划及确保我国核电安全、高效发展奠定重要基础。
1 爆破振动安全判据现状分析
爆破振动安全标准一直为研究热点。国际有德国的DIN4标准、美国的爆破振动安全标准(矿业局(USMBE)及露天矿复垦处(OSMRE)标准)、芬兰标准及瑞典标准等。均对本国建(构)筑物结构、质量、国家整体发展水平等制定相应标准,作为安全管理准则。
我国爆破振动安全普遍采用GB6722-1986标准。该标准为以爆后介质点最大振速作为安全判据。大量工程实例表明,仅用质点振速峰值表示地震动强度远远不够,爆破振动频率也会对爆破安全产生较大影响[3]。考虑爆破振动频率对振动效应影响,新的爆破安全规程(GB6722-2003)采用振速-主频联合判据。该判据考虑不同频率成分的爆破振动分量对结构影响程度差别,以主振频率作为安全判据的重要指标,对于硐室大爆破等主频率较低、频率构成相对集中的爆破振动危害较有效;但对布药分散的工程爆破,由于爆破振动主频高,且频带较宽,与结构自振频率接近的振动分量方对结构起主要破坏作用,而爆破地震动主频率对其所致危害程度并非具有重要作用,而与爆破振动频率分布特征密切相关。另外,振动持时作用亦不容忽视[4]。
为使我国工程爆破振动安全控制标准与国际接轨,需进一步开展相关研究,制定更科学合理、简便实用、可操作性强的新标准。
2 爆破振动信号分形特征
2.1 分形维数计算模型
爆破振动信号为双尺度,即纵向振动幅度及横向时间尺度[2,5]。设爆破振动时程曲线S∈R2,将曲线覆盖的平面R×R划分为尽量小网格k(σ1×σ2)(k=1,2,3,…为网格放大倍数)。图1为用一个基本步长k (σ1×σ2)的矩形覆盖分析信号,并统计对应尺度下有效覆盖网格数Nkσ。
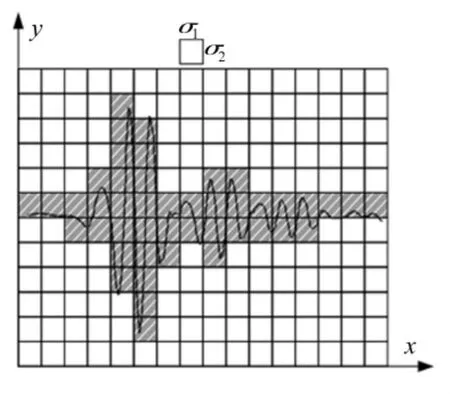
图1 标度δ下总盒数Nkσ(k=1,Nkσ=45)Fig.1 Total number of boxes under measure
设所有与S相交的网格数为Nkσi,在矩形盒覆盖情况下振动曲线盒维数定义[5-8]为
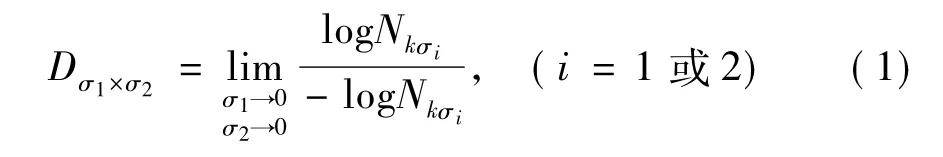
对爆破振动信号这种无函数描述的无规则分形体,只在其无标度区[9]内才具有分形维数。Dσ1×σ2可通过在无标度区内作(-log(Nkσi),log(Nkσi))(i=1或2)双对数拟合曲线斜率求得。
据分析及矩形盒维数定义,在无标度区内-log(kσi)与-log(Nkσi)满足线性回归方程,即
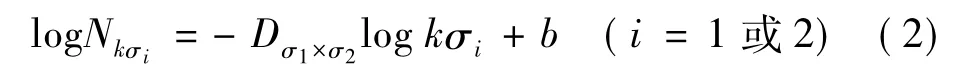
式中:Nkσi=[(max(s(h))-min(s(h))/kσ2]+ φ(rem)(max(s(h))-min(s(h)),kσ2)),h∈(1,n),n为采样点数,φ(x)取值:x>0,φ=1;x=0,φ=0,rem(u,v)为u与v相除的余数。
由于盒维数D是线性式(2)斜率的相反数,在σi值确定的情况下由log(Nkσi)与log(kσi)关系唯一确定。
2.2 矩形盒尺寸确定
考虑分形特性无标度特性要求[5,9],矩形盒尺寸k(σ1×σ2)可据式(1)及爆破振动信号幅值A确定。其中矩形盒宽度kσ1最大不能超过振动信号半周期宽度T/2(半周期T/2由振动波形曲线最高峰值所在波峰的半周期曲线与基准线交点确定)。矩形盒高度kσ2最小值不能小于整个分析信号相邻数据点间最小非零幅值差ΔAmin,kσ2不应大于信号最高峰值Amax。k为矩形盒放大倍数。爆破振动测试信号为离散采样信号,采样时间间隔Δt为有限值,同时其波形表示方式是将两相邻数据点用线段连接,取σ1<Δt无意义,因此k= 1;为体现振动曲线的周期性,矩形盒宽度最大不超过半个主振周期,可确定k的最大取值k=[T/2Δt]+1 (中括弧表示取整)。
2.3 爆破振动信号分形维数计算
确定矩形盒尺寸σ2及k的取值范围后,据式(1)、式(2),经Matlab编程可在确定的无标度区间内统计出每个k值条件下该尺寸大小的矩形盒覆盖爆破振动曲线盒数量Nkσi,再将对应的-log(kσi)与log(Nkσi)进行线性拟合获得参量D,b。
实测爆破振动信号见图2。图3为图2中-log(kσi),log(Nkσi)拟合曲线,其方程为
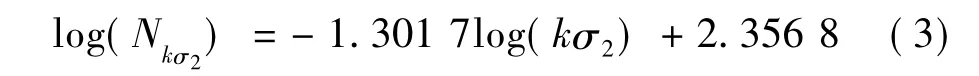
该爆破振动信号的盒维数D=1.301 7,b= 2.356 8。
表1为田湾核电扩建工程中爆破振动监测实验数据及相应爆破振动信号的分形维数计算结果。数据分析表明,实验所有采集的爆破振动信号分形维数值均处于[1,2]之间,符合分形理论中分形曲线分形维数定义及特征要求[9]。并通过大量爆破振动实测数据分析结果验证爆破振动时程曲线具有分形特征的结论可信、无疑。
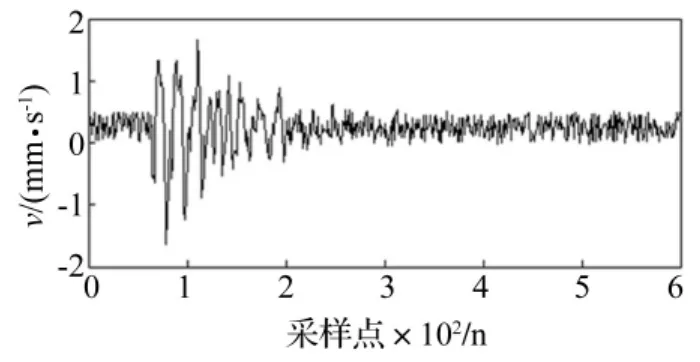
图2 实测爆破振动信号sFig.2 Measured blasting vibration signal
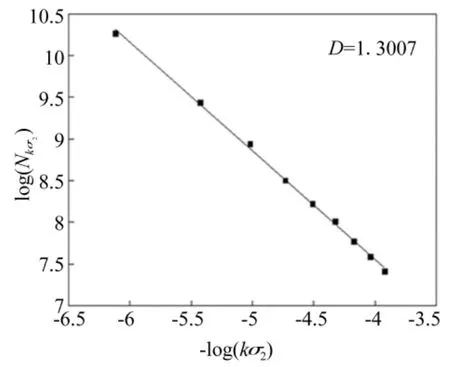
图3 -log(kσ2)~log(Nkσ2)关系曲线Fig.3 Relationship of-log(kσ2)~log(Nkσ2)
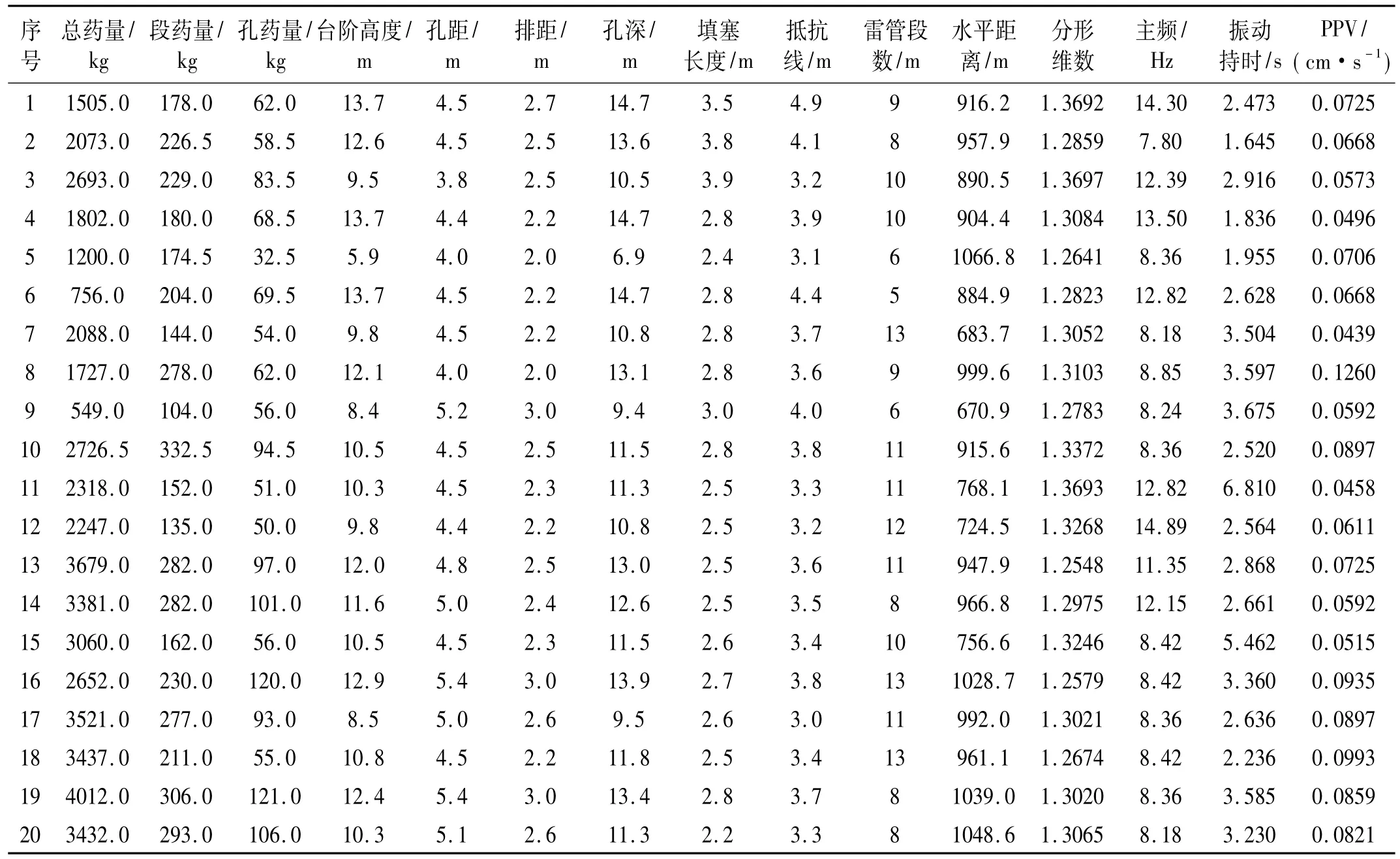
表1 爆破振动测试数据Tab.1 Test data of blasting vibration
3 基于分形理论的爆破振动安全标准探讨
由于研究已充分证明爆破振动信号具有分形特征。因此尝试建立基于分形理论的爆破振动新安全标准。定义参数:①vc为质点振动速度,可采用萨氏公式计算;②vcr为临界速度,即确保建(构)筑物安全的质点速度,由现场实测获得;③vf为计频速度,即考虑频率影响的质点振动速度;④vt为计持时速度,即考虑振动持续时间的质点振动速度;⑤Dx为分形影响系数;⑥Df为频率影响分形系数;⑦Dt为振动持时影响分形系数。
为在爆破振动安全标准中体现出质点振动速度、频率、持时三要素影响,引入折合速度,即,

式中:Dx为分形影响系数,受频率影响分形系数Df及振动持时影响分形系数Df综合影响。即

当质点振动速度vc较小、爆破地震波能量尚不足使结构进入塑性阶段时,爆破振动持时对结构不会有明显的破坏作用,且爆破振动持时往往较短,对结构破坏作用不突出,可近似处理Dt≈1,仅考察频率因素对爆破振动安全标准影响,此时折合速度为计频速度,即

按未考虑振动频率对安全标准造成影响,若vc<vcr,爆破振动不会对设施物产生破坏作用。由式(6)知,vc<vf,即未考虑振动频率影响的质点振动速度小于考虑频率影响的质点振动速度。由于以前爆破振动安全标准忽略该因素,可能导致即使满足vc<vcr,建(构)筑物却发生破坏现象。因此,应对现行安全标准进行修正并提出新的爆破振动安全标准。为确保工程爆破安全,须采用计频速度vf与临界速度vcr进行比较,判别爆破振动是否安全。
只有当满足vf<vcr条件时,才能确保爆破安全。为确保爆破施工过程中的爆破安全,联合式(6)可知,应该满足条件

式中:vs=vcr/Df称为计频允许振速。
当vc<vs时,即地面质点振动速度只有在小于计频允许振速条件下,才不会产生爆破振动危害效应。此可作为判别爆破振动安全的新标准。分析国内外最新研究成果[4,10]并结合本文实验所得大量爆破振动测试数据分析结果,可获得受频率影响分形系数Df与振动频率f之关系,见表2。
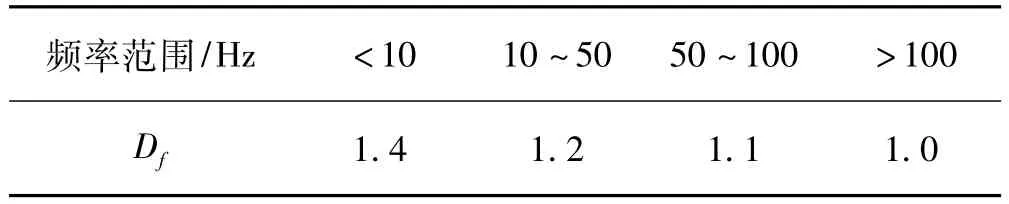
表2 Df与f关系Tab.2 Relationship of Df~f
田湾核电站建设规模为8台百万千瓦级压水堆核电机组,1-2号机组已投入运行,目前正进行3-4号机组基坑爆破开挖。考虑1-2号机组及周边设施已建成,5-6号机组土建施工也同时展开,扩建工程周边需保护的对象多、距离近、环境复杂,见图4。因此如何控制3-4号机组基础爆破开挖时产生的地震动效应对1-2号机组正运行核电设施的危害影响,同时确保运行核电机组的安全稳定运营成为核电集团、爆破施工单位、安全管理主管部门等共同面临的重大技术难题。
由于目前尚未从根本上认识爆破地震波作用时运营状态下常规岛、主控机房、网控楼、气象站等主要核电设施的振动响应机理和破坏模式,缺乏足够的相关理论分析及可信的数值计算成果,难以定量评估核电扩建工程中爆破施工对正运行核电设施结构安全稳定性造成的影响程度。因此,仅能在较大安全系数前提下,以限制爆破作业范围、降低施工进度为代价,对核电扩建工程中爆破作业范围、一次齐爆药量等进行严格控制。该站3-4号机组基坑爆破开挖时爆破振动安全控制主要通过现场试验并结合萨道夫斯基公式得到临界速度值,见表3。
随核电扩建工程不断推进,以前的爆破振动安全标准已不能满足需要,须进行安全修正。核电扩建爆破工程产生的主振频率一般较小,约20 Hz。据表1取Df=1.2。据式(7)获得可靠计频允许振速,见表4。据此判据,可确保田湾核电站扩建工程的爆破施工安全。

表3 田湾核电站石方爆破最大允许振速Tab.3 Maximum allowable quantity and blasting vibration velocity in Tianwan nuclear power station blasting

表4 田湾核电站石方爆破现行最大允许振速Tab.4 Current maximum allowable quantity and blasting vibration velocity in Tianwan nuclear power station blasting
当质点振动速度vc足以使结构进入塑性阶段、且爆破振动持时到几秒情况下,爆破振动破坏效应会非常严重。持时较长的爆破振动作用可能使已在强振中进入塑性状态甚至破坏的结构在持续爆破地震动作用下因疲劳而加剧破坏甚至倒塌。爆破振动持时在地震波对结构破坏起关键性作用。此时Dt≠1,通过大量爆破振动测试数据统计分析结果,可得受振动持时影响的分形系数Dt与振动持时t之关系,见表5。鉴于爆破的总装药量及雷管段数是决定爆破地震动持时的主要因素,在爆破工程实践中应据爆破现场条件及周围环境合理进行爆破方案设计并优化,严格控制总装药量、雷管段数,有效控制爆破地震动的持续作用时间,达到减小爆破振动危害效应目的,确保爆破安全。

表5 Dt与t关系Tab.5 Relationship of Df~t
4 结论
(1)考虑爆破振动信号具有分形特征,为能在运行核电设施在爆破振动激励下的安全标准中体现出质点振动速度、频率、持时三要素影响,在分形影响系数基础上引入折合速度vz作为爆破振动安全评判的新标准,为使我国工程爆破振动安全控制标准与国际接轨奠定了一定基础。
(2)通过田湾核电爆破施工中大量实验测试数据统计结果获得受频率影响分形系数Df与振动频率f之关系、振动持时影响分形系数Dt与振动持时t之关系。通过工程监测实验数据表明基于分形理论的爆破振动安全标准科学、合理,具有较好的工程应用前景。
[1]谢先启.精细爆破[M].武汉:华中科技大学出版社,2010.
[2]谢全民,龙源,田作威,等.爆破振动信号时频特征的三维分形特性研究[J].振动与冲击,2010,29(12):122-126.
XIE Quan-min,LONG Yuan,TIAN Zuo-wei,et al.Threedimensional fractal study on time-frequency characteristics of blast vibration signal[J].Journal of Vibration and Shock,2010,29(12):122-126.
[3]魏晓林,郑炳旭.爆破震动对邻近建筑物的危害[J].工程爆破,2000,6(3):22-25.
WEI Xiao-lin,ZHENG Bing-xu.Destructive effect of blasting vibration on nearby structures[J].Engineering Blasting,2000,6(3):22-25.
[4]言志信,彭宁波,江平,等.爆破振动安全标准探讨[J].煤炭学报,2011,36(8):1281-1284.
YAN Zhi-xin,PENG Ning-bo,JIANG Ping,et al.Research about blasting vibration safety criteria[J].Journal of China Coal Society,2011,36(8):1281-1284.
[5]谢全民,龙源,钟明寿.小波包与分形组合技术在爆破振动信号分析中的应用研究[J].振动与冲击,2011,30(1): 12-16.
XIE Quan-min,LONG Yuan,ZHONG Ming-shou.et al. Applicationofwaveletpacketandfractalcombination technology in blasting vibration signal analysis[J].Journal of Vibration and Shock,2011,30(1):12-16.
[6]谢全民,龙源,钟明寿.小波与分形组合技术在爆破振动信号分析中的应用[J].振动与冲击,2011,30(12):120-124.
XIE Quan-min,LONG Yuan,ZHONG Ming-shou.et al. Blasting vibration signal analysis with wavelet and fractal portfolio analysis technique[J].Journal of Vibration and Shock,2011,30(12):120-124.
[7]娄建武,龙源,徐全军,等.爆破地震信号分形盒维数值分析[J].爆炸与冲击,2004,24(4):363-369.
LOU Jian-wu,LONG Yuan,XU Quan-jun,et al.A study on the fractal dimension of blasting seismic waves[J].Explosion and Shock Waves,2004,24(4):363-369.
[8]娄建武,龙源,徐全军,等.爆破地震信号分形维数计算的矩形盒模型[J].振动与冲击,2005,24(1):81-84.
LOU Jian-wu,LONG Yuan,XU Quan-jun,et al.Study on double-scaled rectangle box model of blasting seismic wave's fractal dimension computation[J].Journal of Vibration and Shock,2005,24(1):81-84.
[9]肯尼思·法尔科内著.分形几何-数学基础及其应用[M].沈阳:东北大学出版社,1991.
[10]蔡路军,马建军,江兵,等.考虑振动频率的爆破振动安全标准的探讨[J].黄金,2006,27(3):24-26.
CAI Lu-jun,MA Jian-jun,JIANG Bing,et al.Discussion on the safety criterion of blasting vibration considering the effect of vibration frequency[J].Gold,2006,27(3):24-26.
New safety standards for running nuclear power facilities under blasting vibration
GUO Tao1,XIE Quan-min2,LIU Qiang1,FAN Lei1,SHEN Wei1
(1.College of Field Engineering,PLA Univ.of Sci.&Tech.,Nanjing 210007,China; 2.Wuhan Ordance N.C.O Academy of PLA,Wuhan 430075,China)
The safety control of running nuclear power facilities inspired by blasting seismic wave is an important subject relating the safety of nuclear power plants.China is building or extending nuclear power bases,and blasting methods will be widely used in front-end foundation excavation,and blasting danger will threaten the safety of running nuclear power facilities.New safety standards against blasting vibration,applicable in nuclear power expansion projects was discussed based on the fractal theory.The results have guiding significance in further standardizing and restraining engineering blasting implementation nearby the running nuclear power facilities and will lay important basis to work out the national planning and ensure the safety of nuclear power plants in China.
blasting vibration;nuclear power facilities;safety standards;fractal
TD235.1;O384
A
10.13465/j.cnki.jvs.2015.02.004
国家自然科学基金资助(51208508);国家自然科学基金资助(51204071)
2013-08-26修改稿收到日期:2013-11-15
郭涛男,博士生,1978年5月生邮箱:guotaogu@sina.com

