改进的高维搜索算法在图像匹配中的应用

王佩文

（四川大学计算机学院，成都 610065）

改进的高维搜索算法在图像匹配中的应用

王佩文

（四川大学计算机学院，成都 610065）

针对现有的高维数搜索算法在进行图像匹配中存在大量错配点对的问题，提出一种基于KD-Tree的改进算法（PCAKD-Forest）。该方法将数据集分解成等量的N个子数据集，针对每个子数据集单独建树。建树时，使用PCA算法，根据各维数之间的协方差，求出它们的主成分奉献率，再按主成分奉献率进行维数优先级排序。将N棵树形成的KDForest应用于图像特征点匹配。实验结果表明，改进后的算法在保证实时性的同时，显著地提高匹配精度。

搜索算法；分区；图像匹配；精度

0 引言

高维数搜索在很多计算机视觉应用中是一个非常重要的组成部分。高维搜索技术发展至今，已经拥有很多经典的算法，例如等距索引、Opt-Tree、C-Tree、hBTree，等等。在众多的高维搜索算法当中，K维搜索树因其良好的实时性在图像匹配中被广泛地应用。但是，随着样本数据集当中特征点数量的增多，K维搜索树算法一般只能匹配到较近的点，而无法匹配到最近点，同时还有一些错配点。针对以上不足，本文提出一种基于K维搜索树的PCA-KD-Forest算法，该算法形成多棵有序K维搜索树。实验表明，该算法显著地提高了匹配精度，同时保持了良好的实时性。

1 K维搜索树及图像匹配算法简介

K维搜索树——即KD-Tree（KD树），是一种高维索引树形数据结构，常用于大规模的高维数据空间进行最近邻查找和近似最近邻查找，例如图像检索和识别中的高维图像特征向量的K近邻查找与匹配。下面分析KD-Tree的基本原理。

1.1 K维搜索树的构造

构建KD-Tree时，在树的第一层（根），先选定一个最大方差维度，因为数据在该维度上分散得比较开，更容易在这个维度上将数据划分开。然后计算该维度上数据的中值，以此作为划分阈值，此时数据被一个垂直于该维度的超平面分割成两半。然后每半数据用相同的方法递归分割来创建一棵完全平衡的二叉树。

1.2 最近邻查找

（1）将查询数据Q从根结点开始，按照Q与各个结点的比较结果向下访问KD-Tree，直至达到叶子结点。其中Q与结点的比较指的是将Q对应于结点中的k维度上的值与中值z进行比较，若Q（k）〈z，则访问左子树，否则访问右子树。达到叶子结点时，计算Q与叶子结点上保存的数据之间的距离，记录下最小距离对应的数据点，记为当前“最近邻点”P和最小距离D。

（2）进行回溯（Backtracking）操作，该操作是为了找到离Q更近的“最近邻点”。即判断未被访问过的分支里是否还有离Q更近的点，它们之间的距离小于D。如果Q与其父结点下的未被访问过的分支之间的距离小于D，则认为该分支中存在离P更近的数据，进入该结点，进行步骤（1）一样的查找过程，如果找到更近的数据点，则更新为当前的“最近邻点”P，并更新D。如果Q与其父结点下的未被访问过的分支之间的距离大于D，则说明该分支内不存在与Q更近的点。回溯的判断过程是从下往上进行的，直到回溯到根结点时已经不存在与P更近的分支为止。

1.3 图像特征匹配算法

Sift算法是经典的图像特征点匹配算法，由128维的数据作为描述子，将两个高维数据的欧氏距离作为匹配准则。Sift算法包括以下五个步骤：

①建立尺度空间极值。尺度空间函数等于可变尺度的高斯函数G（x，y，σ）与输入图像I（x，y）的卷积，公式如下：

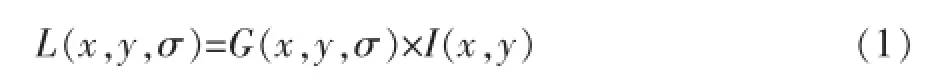
其中：

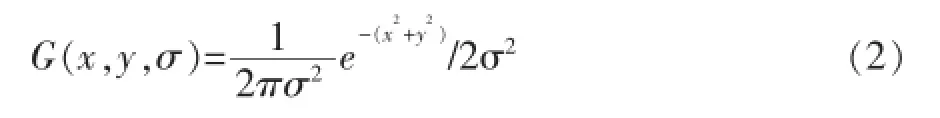
通过建立高斯金字塔来求取特征点的位置，高斯金字塔是通过对输入图像进行降采样形成的图像组。为了有效获取稳定的特征点位置，采用差分高斯金字塔DOG，即：

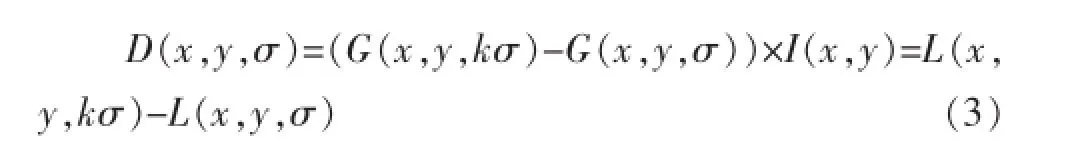
②去除不可靠的特征点。

③特征点方向分配。每个特征点都被分配一个或多个方向基于梯度直方图。

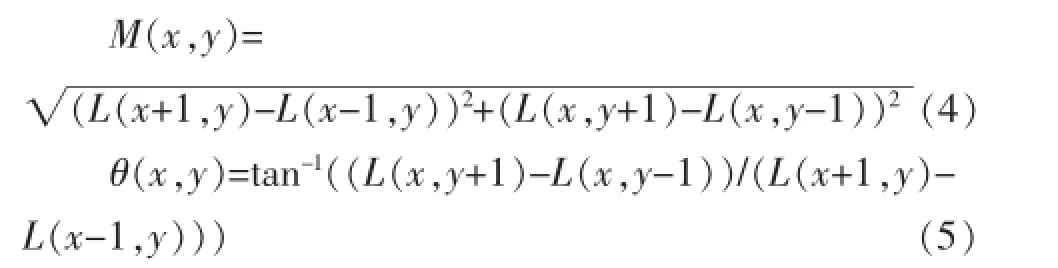
式（4）和式（5）分别为（x，y）处梯度的模值和方向计算公式。每个特征点被指定一个主方向和一个辅方向，这样，每个特征点都包含位置、尺度以及方向三个信息。

④生成特征描述符。局部图像梯度是在每个特征点区域已经选择好的尺度下检测的。特征描述符是由特征点周围的16×16像素领域内计算的，将领域分成4×4的子块，然后对每个子像素块计算8个方向的梯度方向直方图。这样每个特征点的特征向量是128维（4× 4×8）。

⑤匹配。求参考图像中的每个特征点在测试图像中特征点集中最近与次近的特征点；若最近与次近的比率小于某个给定阈值，则认为正确匹配，否则不匹配；这里的最近与次近定义为特征点的描述符向量的欧氏距离。

2 PCA-KD-Forest算法

K维搜索树算法在进行高维空间特征点匹配时，随着样本点的增多，准确率会快速下降，一般只能匹配到相近的点，而无法匹配到最近的点，甚至会出现很多错配点。而且样本点的维数越高，越容易在之前的维数对特征点进行错分，导致错配率升高。PCA-KD-Forest算法针对以上不足，提高搜索准确性，提高匹配精度，它是在K维搜索树的基础上加以改进的，其步骤如下：

①首先利用Sift算法提取参考图像与测试图像的特征点，设参考图像与测试图像提取的特征点个数分别为Nr与Nt，设参考图像的特征点集合为Sr=｛Xr（0），Xr（1），…，Xr（Nr－1）}，测试图像的特征点集合为St=｛Xt（0），Xt（1），…，Xt（Nt－1）｝；

②将参考图像特征点集Sr划分为F个分区，每个分区单独建树，经实验表明，当F=9时，既能保持原有算法实时性，又能提高匹配精度；

④计算相关矩阵R=r（i，j），如式（6）：

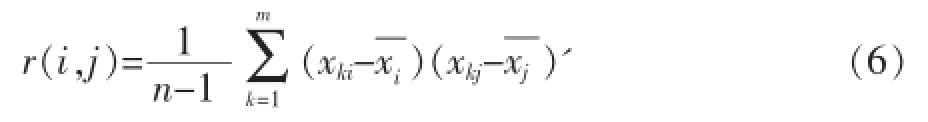
⑤由|R-λiI|=0，求得特征值和特征向量，其中λi表示主成分的方差贡献；

⑥计算主成分贡献率如式（7）：

⑦按照Ci，得到数组E[n]，它根据主成分贡献率从大到小存储特征点的维数；

⑧按照E[n]中维数的顺序，构造K维搜索树，由F棵K维搜索树形成有序的KD-Forest；

⑨将测试图像中的特征点，依次在有序KD-Forest中的每棵K维搜索树中进行搜索，用欧氏距离计算，得到F个相近点，比较这F个相近点，取其中距离最小的点作为最近点，此时算法终止。

3 实验及结果分析

为了验证本文提出的PCA-KD-Forest算法的有效性，使用不同内容的图像集，对本文方法与K维搜索树方法做比较。用于本文实验的多组不同图像来自文献[2]中给出的被使用最广泛的图像集，每组图像包含6帧内容一致的图像，在这多组图像中分别包含了视角变化、图像旋转和尺度缩放以及光线改变。实验环境使用的操作系统为Windows 7，CPU为1.70 GHz，内存为4G，程序运行环境为Visual Studio 2008。

从图像集中选一组针对不同角度旋转和尺度缩放的图像来进行匹配正确率对比，图1为用于实验的其中两帧图像，图1（a）为参考图像，图1（b）为测试图像；图2为两种算法的匹配结果。

图1 用作实验的两帧图像

图2 两种算法的匹配结果

用于实验的多帧图像的尺寸均为原始尺寸，表1为匹配结果数据。

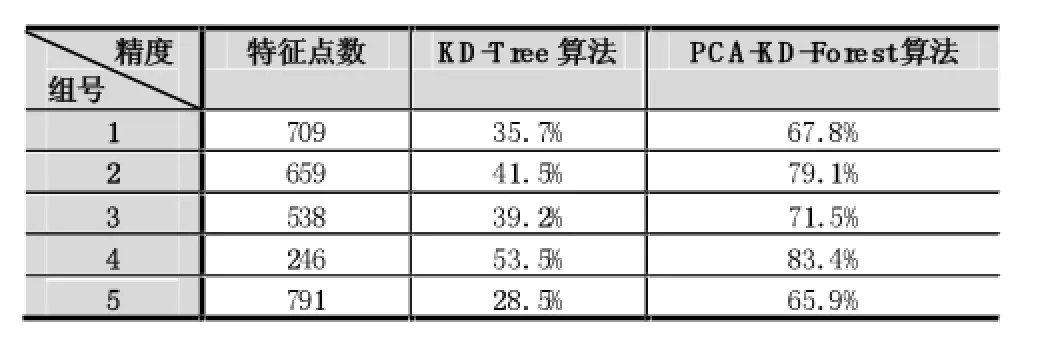
表1 两种算法的匹配数据

上述实验结果表明，PCA-KD-Forest算法相比K维搜索数算法，在精度方面有着显著的提高。

4 结语

本文分析了K维搜索树算法的原理及其存在的缺点，提出了PCA-KD-Forest算法。该算法旨在提高高维数搜索算法的精度，同时保证实时性，因此PCA-KDForest算法具有良好的实际应用价值。

[1] 熊云艳，毛宜军，闵华清.有序的KD-Tree在图像特征匹配上的应用[J].化学自动化仪表，2010，37（10）：84～87

[2] Mikolajczyk K，Tuytelaars T，Schmid C，etc.A Comparison of Affine Region Detectors[J].International Journal of Computer Vision，2005，65（1/2）：43

[3] You Jia，Jingdong Wang，Gang Zeng，Hongbin Zha.Optimizing KD-Trees for Scalable Visual Descriptor Indexing[J].Computer Vision and Pattern Recognition（CVPR），2010：3392～3399

[4] Qian Zhang*，Ning Shan，Feng Chen Qian，Ya Lin Ye.A New Method of Expressing Point Model Based on KD-Tree for Plane Area [J].Advanced Materials Research，2013：658～661

Application of the Improved High-Dimensional Search Algorithm in Image Matching

WANG Pei-wen
（College of Computer Science，Sichuan University，Chengdu 610065）

Since the matching result with traditional high-dimensional search algorithm has many false matching points,proposes an improved highdimensional search algorithm（PCA-KD-Forest）based on KD-Tree.Decomposes the data set into N subsets with the same amount.For each subset,creates a KD-Tree.Uses principal components analysis and calculates the rate of contributions of the main components.According to the covariance between dimensions,the dimensions are sorted by the rate of contributions.Then all KD-trees constitute a KDForest.Applies the improved KD-Forest to match the Sift characteristic point.The experiment demonstrates that the matching accuracy is improved greatly in the premise of real time property.

Search Algorithm;Partition;Image Matching;Accuracy

1007-1423（2015）04-0015-04

10.3969/j.issn.1007-1423.2015.04.004